البرمجة الخطية والحل الأمثل - رياضيات2-1 - ثاني ثانوي

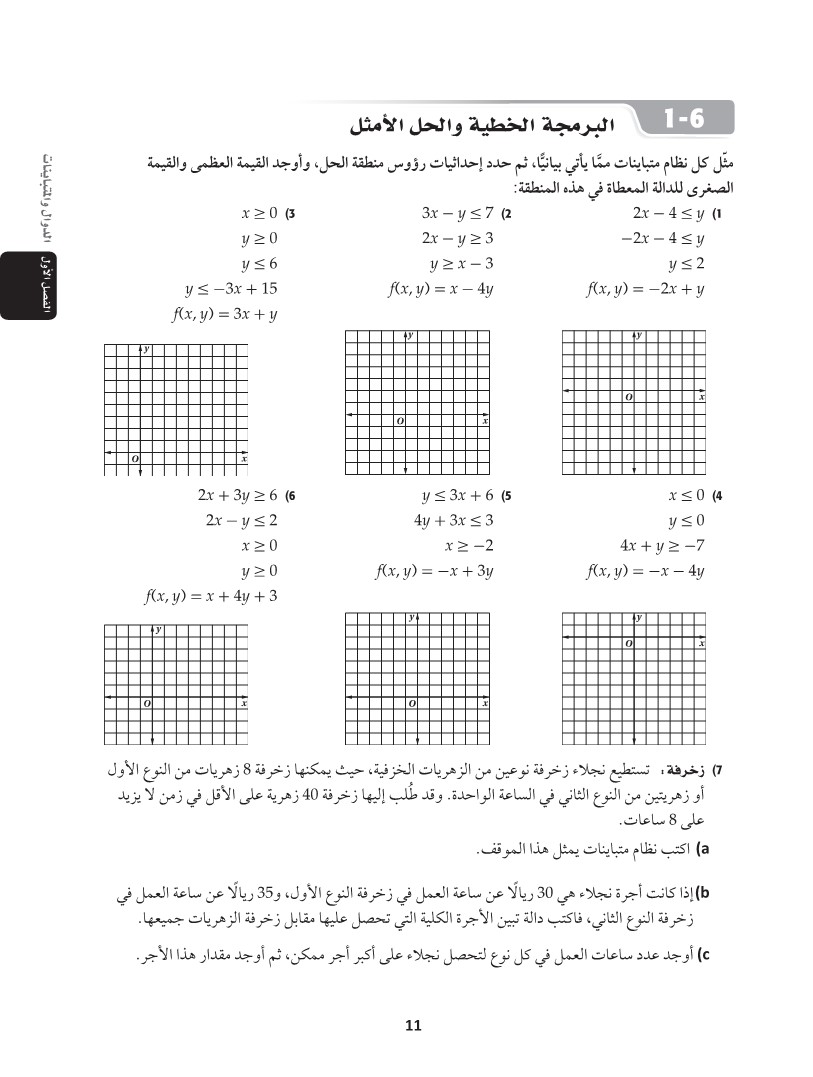
الفصل الأول الدوال والمتباينات 1-6 البرمجة الخطية والحل الأمثل مثل كل نظام متباينات مما يأتي بيانيًا، ثم حدد إحداثيات رؤوس منطقة الحل، وأوجد القيمة العظمى والقيمة الصغرى للدالة المعطاة في هذه المنطقة: x≥0 (3 y≥0 y≤6 y≤-3x+15 f(x, y) = 3x + y 3x - y ≤7 (2 2x-y≥3 2x-4≤y (1 -2x-4≤y y≥x-3 y≤2 f(x, y) = x - 4y f(x, y) = -2x+y 2x + 3y ≥6 (6 2x-y≤2 x20 y≤3x+6 (5 4y + 3x = 3 x≥-2 x ≤0 (4 y≤o 4x + y ≥ -7 y≥0 f(x,y) = - x + 3y f(x, y) = -x-4y f(x, y)=x+4y+3 (7) زخرفة تستطيع نجلاء زخرفة نوعين من الزهريات الخزفية، حيث يمكنها زخرفة 8 زهريات من النوع الأول أو زهريتين من النوع الثاني في الساعة الواحدة. وقد طلب إليها زخرفة 40 زهرية على الأقل في زمن لا يزيد على 8 ساعات. a اكتب نظام متباينات يمثل هذا الموقف. b) إذا كانت أجرة نجلاء هي 30 ريالًا عن ساعة العمل في زخرفة النوع الأول، و35 ريالًا عن ساعة العمل في زخرفة النوع الثاني، فاكتب دالة تبين الأجرة الكلية التي تحصل عليها مقابل زخرفة الزهريات جميعها. c) أوجد عدد ساعات العمل في كل نوع لتحصل نجلاء على أكبر أجر ممكن، ثم أوجد مقدار هذا الأجر. 11

مثل كل نظام متباينات مما يأتي بيانيا

أوجد عدد ساعات العمل في كل نوع لتحصل نجلاء على أكبر أجر ممكن