حل معادلات كثيرات الحدود - رياضيات2-1 - ثاني ثانوي

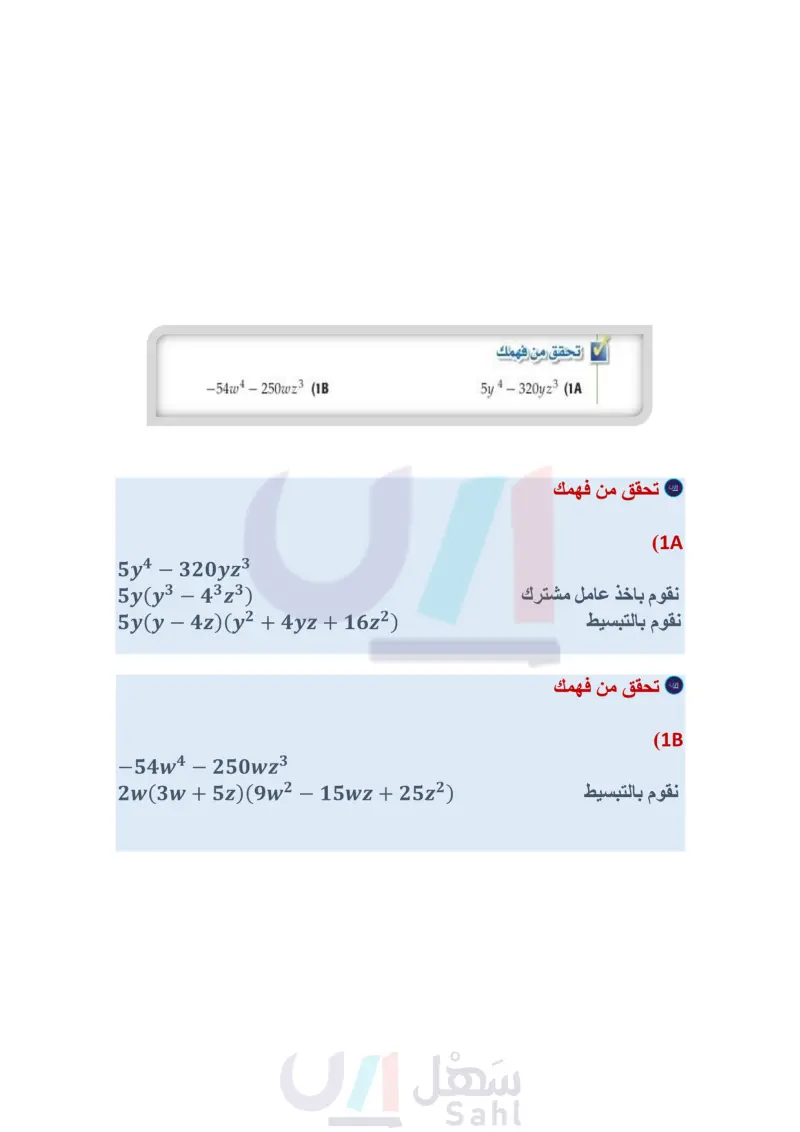
3-6 فيما سبق: بالتحليل إلى العوامل. حل معادلات كثيرات الحدود Solving Polynomial Equations لماذا؟ الجزء درست حل معادلات تربيعية قطع مكعب صغير من آخر كبير كما في الشكل المجاور، وأُعطي حجم المتبقي والعلاقة بين بعدي المكعبين والمطلوب إيجاد أبعاد المكعبين الصغير والكبير. لاحظ أنه يمكن إيجادها بتحليل كثيرة الحدود التكعيبية 3-x3. (الدرس 2 - 3 ) والآن : أحلل كثيرات الحدود. ▪ أحل معادلات كثيرات تحليل كثيرات الحدود: تعلمت سابقًا أنه يمكنك تحليل كثيرات الحدود رابط الدرس الرقمي www.ien.edu.sa التربيعية تمامًا كما تحلل الأعداد الكلية، ولكن عواملها ستكون كثيرات حدود أخرى، وكما هو الحال في الحدود بالتحليل إلى العوامل. المفردات كثيرة حدود أولية كثيرات الحدود التربيعية يمكنك تحليل بعض كثيرات الحدود التكعيبية بقوانين خاصة. مفهوم أساسي مجموع مكعبين والفرق بينهما أضف إلى مطويتك prime polynomial الصورة التربيعية quadratic form طريقة التحليل مجموع مكعبين الفرق بين مكعبين الحالة العامة b3 : a³+b³ = (a+b)(a² - ab + b²) a³ — b³ = (a - b)(a² + ab + b²) تُسمى كثيرة الحدود التي لا يمكن تحليلها إلى كثيرتي حدود درجة كل منهما أقل من درجة كثيرة الحدود المعطاة كثيرة حدود أولية. مثال 1 مجموع مكعبين والفرق بينهما إرشادات للدراسة التحليل التام لكثيرات الحدود حلل كلًا من كثيرتي الحدود الآتيتين تحليلا تاما، وإذا لم يكن ذلك ممكنا، فاكتب كثيرة حدود أولية : 16x4 + 54xy3 (a 16x4 + 54xy3 = 2x (8x3 + 27y3) أخرج العامل المشترك الأكبر يعد تحليل كثيرة الحدود تحليلا تاما إذا كتبت في صورة ناتج ضرب كثيرات حدود جميعها أولية، أي إذا حللت إلى أقصى درجة كل من 8x3 و 27y3 مكعب كامل، لذا تستطيع استعمال طريقة مجموع مكعبين. 8x3 + 27y3 = (2x) 3 + (3y )3 8x3 = (2x)3; 27y3 = (3y)3 ممكنة. = (2x + 3y)[(2x)² - (2x)(3y) + (3y)²] = = (2x + 3y)(4x² - 6xy + 9y²) 16x4 + 54xy3 = 2x (2x + 3y) (4x2 - 6xy + 9y2) مجموع مكعبين بسط اكتب العامل المشترك الأكبر 8y3 + 5x2 (b الحد الأول مكعب كامل، لكن الحد الثاني ليس كذلك، لذا لا يمكن تحليل كثيرة الحدود باستعمال طريقة مجموع مكعبين، ولا يمكن تحليلها كذلك بطرائق تحليل كثيرات الحدود التربيعية، أو بإخراج العامل المشترك الأكبر؛ لذا فهي كثيرة حدود أولية. تحقق من فهمك 5y4 - 320yz³ (1A -54w4-250wz3 (1B وزارة التعليم Ministry of Education الدرس 6- حل معادلات كثيرات الحدود 14 2145

إرشادات للدراسة. التحقق من الإجابة: للتحقق من صحة إجابتك اضرب العوامل لتتحقق من صحة تحليل كثيرة الحدود. 146 يلخص الجدول الآتي معظم الطرائق المستعملة لتحليل كثيرات الحدود، وعندما تريد تحليل كثيرة حدود ابحث أولا عن العامل المشترك الأكبر، ثم حدد ما إذا كانت كثيرة الحدود الناتجة بعد إخراج العامل المشترك الأكبر قابلة للتحليل أم لا مستعملا واحدة أو أكثر من الطرائق المذكورة في الجدول أدناه: ملخص المفهوم طرائق التحليل عدد الحدود طريقة التحليل إخراج العامل المشترك الأكبر أي عدد حدان الفرق بين مربعين مجموع مكعبين الفرق بين مكعبين ثلاثية حدود المربع الكامل ثلاثة حدود ثلاثية الحدود بالصورة العامة أربعة حدود أو أكثر تجميع الحدود مثال 2 التحليل بتجميع الحدود نموذج أضف إلى مطويتك 4a3b28ab4ab(a²b - 2) a² = b² = (a + b)(a − b) a³ + b³ = (a+b)(a² − ab + b²) a³ – b³ = (a - b)(a² + ab + b²) - a²+2ab+b² = (a + b)² a22ab+b² = (a - b)² acx2 + (ad + bc)x + bd = (ax + b) ( x ) d ax + bx+ay + by = x(a + b) + y(a+b) = (a + b)(x + y) حلل كلًا من كثيرتي الحدود الآتيتين تحليلا تاما، وإذا لم يكن ذلك ممكنًا، فاكتب كثيرة حدود أولية: 8ax + 4bx + 4cx + 6ay + 3by + 3cy a 8ax + 4bx + 4cx + 6ay + 3by + 3cy = (8ax + 4bx + 4cx) + (6ay + 3by + 3cy) = 4x(2a+b+c) + 3y (2a + b + c) (4x+3y)(2a + b + c) = 20fy - 16fz + 15gy + 8hz - 10hy - 12gz (b 20fy - 16fz + 15gy + 8hz - 10hy - 1282 = (20fy + 15gy – 10hy) + (−16fz — 12gz + 8hz) = 5y (4f + 3g − 2h) − 4z(4f + 3g — 2h) تحقق من فهمك = (5y — 4z)(4f + 3g − 2h) - 30ax - 24bx+6cx - 5ay² + 4by² - cy² (2A 13ax + 18bz - . 15by - 14az (2) العبارة الأصلية جمع لإخراج العامل المشترك الأكبر أخرج العامل المشترك الأكبر لكل تجميع خاصية التوزيع العبارة الأصلية جمع لإخراج العامل المشترك الأكبر أخرج العامل المشترك الأكبر لكل تجميع خاصية التوزيع تُعد طريقة التحليل بتجميع الحدود هي الطريقة الأساسية لتحليل كثيرات الحدود المكونة من أربعة حدود أو أكثر، أما كثيرات الحدود المتضمنة حدين أو ثلاثة حدود فيمكنك تحليلها اعتمادًا على إحدى الطرائق الموجودة في الجدول أعلاه . وزارة التعليم الفصل 3 كثيرات الحدود ودوالها Ministry of Education 2024-1446

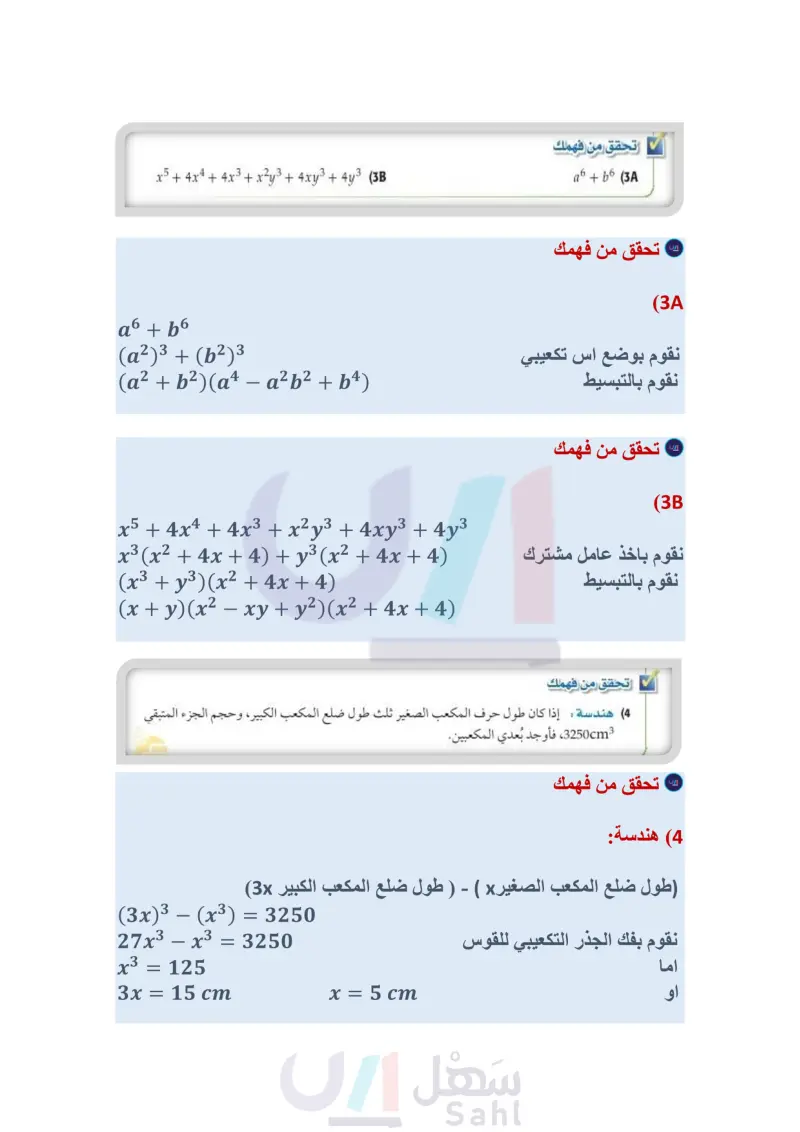
2x إرشادات للدراسة التحليل باستعمال الفرق بين مكعبين : في مثال 3a، إذا بدأت بالتحليل على اعتبار أن مثال 3 التحليل باستعمال الفرق بين مربعين، ومجموع مكعبين، والفرق بين مكعبين حلل كلًا من كثيرتي الحدود الآتيتين، وإذا لم يكن ذلك ممكنا فاكتب كثيرة حدود أولية: - x6 — y6 (a أن يتم يمكن اعتبار كثيرة الحدود هذه فرقًا بين مربعين أو فرقا بين مكعبين، وفي مثل هذه الحالة يجب أن التحليل أولا على اعتبار أنها فرق بين مربعين قبل التحليل على اعتبار أنها فرق بين مكعبين؛ تسهيلًا للتحليل. (x6 - y6 = (x3 + y3)(x3 - y3 الفرق بين مربعين = (x + y)(x² - xy + y²)(x − y)(x² + xy + y²) a3x2 – 6a3x + 9a3 - b3x2 + 6b3x - 963 (b كثيرة الحدود المعطاة فرق بين مكعبين؛ فإنك تحصل على التحليل التالي: 4 2 (x²-y²) (x²+x² y²+y4) وهو تحليل غير تام ويصعب إتمامه. إرشادات للدراسة تجميع 6 حدود أو أكثر جمع الحدود التي بينها أكبر عدد من العوامل المشتركة. بما أن كثيرة الحدود هذه من 6 حدود ، إذن حلل أولا بتجميع الحدود. مجموع مكعبين والفرق بين مكعبين جمع لإخراج العامل المشترك الأكبر أخرج العامل المشترك الأكبر لكل تجميع خاصية التوزيع الفرق بين مكعبين ثلاثية حدود المربع الكامل a3x2 – 6a3x + 9a3 - b3x2 + 6b3x - 963 = (a3x2 - 6a3x + 9a3) + (-b3x2 + 6b3x - 963) = a3x2 - 6x + (9) - b3 (x2 - 6x + (9) = = (a3b3)(x²-6x+9) (a - b)(a² + ab + b²)(x² - 6x + 9) = (a - b)(a² + ab + b²)(x-3)2 x5 + 4x4 + 4x3 + x2y3 + 4xy3 + 4y3 (3 تحقق من فهمك a6 +66 (3A حل معادلات كثيرات الحدود يمكنك تطبيق طرائق حل المعادلات التربيعية في حل معادلات كثيرات الحدود ذات الدرجات الأعلى من الدرجة الثانية. مثال 4 من واقع الحياة حل معادلات كثيرات الحدود بالتحليل هندسة: ارجع إلى فقرة لماذا في بداية هذا الدرس. إذا كان طول حرف المكعب الصغير يساوي نصف طول ضلع المكعب الكبير ، وحجم الجزء المتبقي 7000cm3، فما بعدا المكعبين؟ بما أن طول حرف المكعب الصغير يساوي نصف طول ضلع المكعب الكبير فيمكن أن يعبر عن طول ضلع المكعب الصغير بـ x ، وطول ضلع المكعب الكبير بـ 2x. لاحظ أن الجزء المتبقي يساوي حجم المكعب الكبير مطروحًا منه حجم حجم المكعب الصغير. .2x- 2x حجم الجزء المتبقي 8x3 = (2x)³ بالطرح اقسم على 7 للطرفين اطرح 1000 من كلا الطرفين فرق بين مكعبين خاصية الضرب الصفري (2x)3x3 = 7000 8x3 - x3 = 7000 7x3 = 7000 x3 = 1000 x31000 = 0 (x - 10)(x2 + 10x + 100) = 0 x2 + 10x + 100 = 0 x = -5 ± 5i3 أو X - 10 = 0 x = 10 وبما أن العدد 10 هو الحل الحقيقي الوحيد فإن طولي ضلعي المكعبين هما 10cm,20cm. تحقق من فهمك (4) هندسة: إذا كان طول حرف المكعب الصغير ثلث طول ضلع المكعب الكبير، وحجم الجزء المتبقي 3 3250cm، فأوجد بعدي المكعبين. وزارة التعليم Ministry of Education الدرس - حل معادلات كثيرات الحدود 2147144

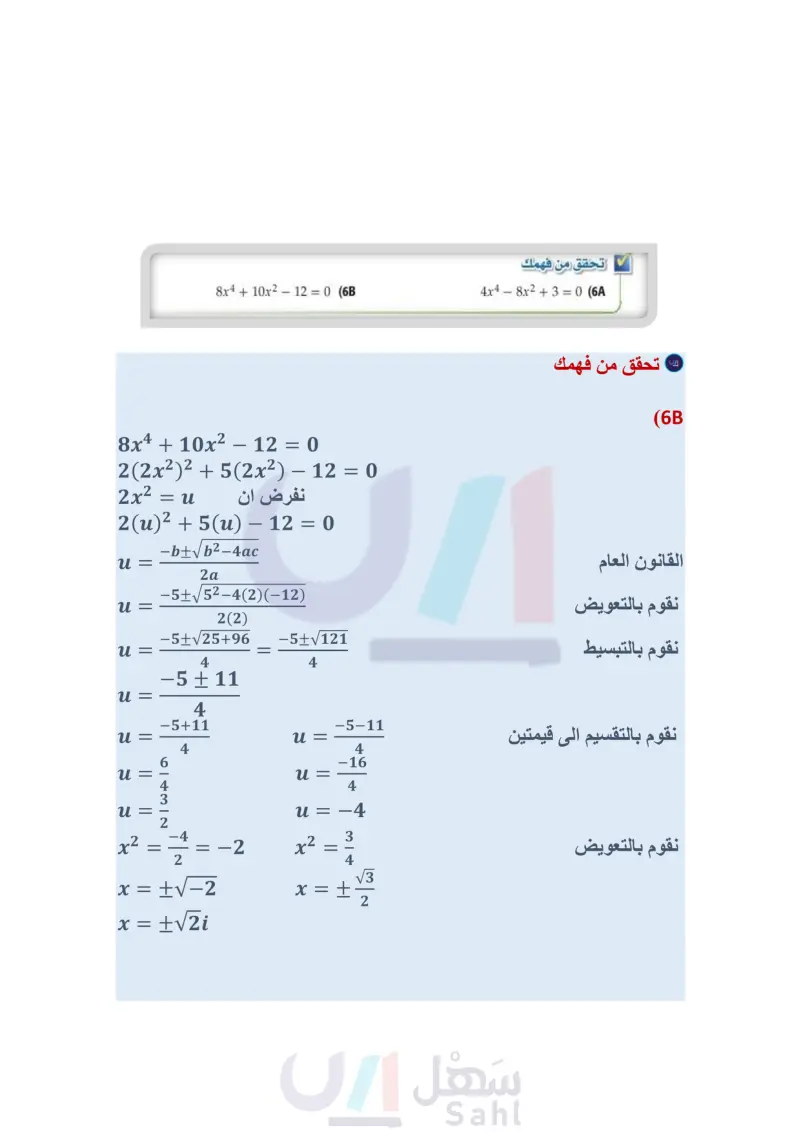
إرشادات للدراسة الصورة التربيعية لكتابة كثيرة حدود على الصورة التربيعية، اختر العبارة المكافئة لـ ا بالنظر إلى الحدود التي تحوي متغيرات واهتم خصوصًا بأسس المتغير الأصلي في bu ، فمثلًا بفرض أن u = x2 6 تستطيع أحيانًا أن تكتب كثيرة حدود فيها المتغير x على الصورة au يمكنك كتابة كثيرة الحدود 32 + 2 x 4 + 12x على الصورة 32 + x 2) 2 + 12x2) أو 32 + u2 + 12u . وكثيرة الحدود الجديدة هذه تكافئ كثيرة الحدود الأصلية، ولكنها مكتوبة على الصورة التربيعية. مفهوم أساسي الصورة التربيعية أضف إلى مطويتك التعبير اللفظي: الصورة التربيعية لكثيرة الحدود هي: a,b,c ، a0، au2+bu أعداد حقيقية، ويمكن أن نكتب بعض كثيرات الحدود في المتغير x على هذه الصورة، وذلك بعد تعريف 4 بدلالة x مثال : 12x6 +8x³ +1 = 3(2x³)² + 4(2x³) +1 مثال 5 كتابة عبارات في الصورة التربيعية اكتب كلا من العبارتين الآتيتين في الصورة التربيعية إن أمكن ذلك: 150n 40n4-15 (a ابحث عن عاملين للعدد 150؛ أحدهما مربع كامل، وعن عاملين للعدد 40؛ أحدهما الجذر التربيعي لأحد عاملي العدد 150. 150n840n4 - 15 = 6×25n8 +8x5n4 - 15 = 6(5n4)² + 8(5n4) – 15 y8 + 12y3 + 8 (b لا يمكن كتابتها على الصورة التربيعية؛ لأن (32) + 8. 1506x25, 40 = 8×5 25n8 = (5n4)2 تلك الحدود. فهناك كثيرات حدود لا يمكن كتابتها على الصورة التربيعية. تحقق من فهمك x4 + 5x + 6 (5 8x4 + 12x2 + 18 (53 +18 يمكنك في بعض الأحيان استعمال الصورة التربيعية لحل معادلات كثيرات الحدود ذات درجات أكبر من الدرجة الثانية. مثال 6 حل معادلات كثيرات الحدود باستعمال الصورة التربيعية حل المعادلة : 0 = 3 + 18x4 – 21x2. 148 18x421x2 +3=0 2(3x2)27(3x2) + 3 = 0 242 - 74 + 3 = 0 (2u 1)(u 3) = 0 - - = 3 u = u أو 3x2 = 3 3x2 = x2 = 1 به = 121216 √6 x = +1 x = + 6 √6 √6 6 6 حلول المعادلة هي : 1-1, تحقق من فهمك 4x4 - 8x2 + 3 = 0 (6 الفصل 3 كثيرات الحدود ودوالها المعادلة الأصلية 18x4 = 2(3x²)2 افرض أن 3x2 = 1 حلل إلى العوامل خاصية الضرب الصفري عوض 3x2 بدلا من 4 اقسم على 3 أوجد الجذر التربيعي 8x4 + 10x2 - 12 = 0 (6 وزارة التعليم Ministry of Education 2024-1446

تأكد حلل كلَّ كثيرة حدود مما يأتي تحليلاً تاماً. وإذا لم يكن ذلك ممكنًا، فاكتب كثيرة حدود أولية : الأمثلة 3-1 16g3 + 2h³ (2 a6x2b6x2 (4 3ax + 2ay - az + 3bx (1 129703 - 1294 (3 83 - 125d3 (6 x3y2 - 8x3y + 16x3 + y5 - 8y4 + 1613 (5) 7 إنشاءات صنع أنس ممرا خشبيا عرضه x ft حول بركة مستطيلة مثال 4 الشكل. فإذا كان طول البركة 40ft وعرضها 30، ومساحتها مع الممر 2000f2، فما عرض الممر الخشبي؟ مثال 5 اكتب كلًا من العبارتين الآتيتين على الصورة التربيعية إن كان ذلك ممكنًا: 4x62x3 +8 (8 حل كلًا من المعادلتين الآتيتين: مثال 6 256 - 52 + 20 (9 x46x²+8=0 (10 تدرب وحل المسائل y4 - 18y2 + 72 = 0 (11 حلل كلَّ كثيرة حدود مما يأتي تحليلاً تاما. وإذا لم يكن ذلك ممكنًا، فاكتب كثيرة حدود أولية: الأمثلة 3-1 a8a2b6 (14 64x4 + xy3 (13 8c327d3 (12 gx2 - 3hx2 - 6fy2 - gy2 + 6fx2 + 3hy2 (16 x6y3 + y9 (15 18x6+5y6 (17 8x5 - 25y3 + 80x4 - x2y3 + 200x3 - 10xy3 (18 12ax2 - 20cy2 - 18bx2 - 10ay2 + 15by2 + 24cx2 (19 20) هندسة: إذا كان حجم المجسم المجاور يساوي 55xcm3 حيث 0 < x، فأوجد مثال 4 كلَّا من قيمة x، وطول قاعدته وعرضها، وارتفاعه. x + 3 x - 3 وزارة التعليم Ministry of Education الدرس 6- حل معادلات كثيرات الحدود 14 2149

8x6 6x3+7 (23 اكتب كل عبارة مما يأتي على الصورة التربيعية إن كان ذلك ممكنًا: مثال 5 -15x+18x²-4 (22 x4 + 12x2 - 8 (21 16x10 + 2x5 (26) - 9x8 21x4+12 (25 5x6 - 2x2 + 8 24 حُلَّ كلَّ معادلة مما يأتي: مثال 6 4x4 – 14x2 + 12 = 0 (29 x4 - 3x2 - 10 = 0 28 x4 + 6x2 + 5 = 0 (21 24x414x23=0 (32 4x4 5x26=0 (31 9x4 27x2+20=0 (30 حلّل كلَّ كثيرة حدود مما يأتي تحليلاً تاما، وإن لم يكن ذلك ممكنًا، فاكتب كثيرة حدود أولية: 8x5y2 - 27x2y5 (36) x5-16x (35 x6-64 (34 x4625 (33 15ax – 10bx + 5cx + 12ay - 8by + 4cy + 15az - 10bz + 5cz (37 6a2x2 – 24b2x2 + 18c2x2 - 5a2y3 + 20b2y3 - 15c2y3 + 2a2z2 - 8b2z2 + 6c2z2 (38 6x511x410x3 - 54x³ + 99x² + 90x (39 20x6 - 7x5 - 6x4 - 500x4 + 175x3 + 150x2 (40 حُلَّ كلَّ معادلة مما يأتي: x4 - 7x2 - 44 = 0 43 x416x2720 = 0 (42 x4 + x2 - 90 = 0 41 64x310 (46 x32160 (45 x4 + 6x2 - 91 = 0 44 حل كل معادلة مما يأتي: 6x4 - 5x2 - 4 = 0 48 18x4 + 43x2 – 5 = 0 (50 3x422x245 = 0 (52 4x4 - 4x2 - x2 + 1 = 0 (54) x4 + 8x2 + 15 = 0 (56 8x4 + 10x2 - 3 = 0 47 20x453x²+18=0 (49 8x418x2+4=0 (51 x626x327 = 0 (53 x6 - 9x4 - x2 + 9 = 0 (55 57) هندسة : منشور متوازي مستطيلات أبعاده 6 - x - 2, x - 4,x ، وحجمه 40x وحدة مكعبة. المنشور. a اكتب معادلة كثيرة حدود تمثل حجم ) حل المعادلة باستعمال التحليل إلى العوامل. هل هناك قيم غير مقبولة للمتغير x عند حل المعادلة؟ وضّح إجابتك. وزارة التعليم Ministry of Education 2024-1446 d) ما أبعاد المنشور؟ الفصل 3 كثيرات الحدود ودوالها 150

28 ft 58 تصميم يريد سليمان أن يبني بركة سباحة وفق التصميم المجاور، حيث يحيط بها ممر خشبي بعرض ثابت. إذا كانت مساحة سطح البركة فقط 336ft2، فما قيمة x؟ ( إذا أصبحت قيمة x مثليها وذلك بتقليل مساحة سطح البركة، فما المساحة الجديدة لسطح البركة؟ إذا نصفت قيمة x بزيادة مساحة سطح البركة، فما مساحة سطح البركة فقط عندئذ؟ (59) أحياء قدر حسام عدد الفيروسات في إحدى التجارب بالدالة: 16 ft 24 ft 12 ft 8000 + t) = 0.0123 - 0.24t2 + 6.3t)، حيث الزمن بالساعات (t) عدد الفيروسات. فإذا أراد حسام أن يحدد الزمن الذي يصبح فيه عدد الفيروسات 8000 فيروس. (a فأوجد قيمة t باستعمال التحليل إلى العوامل. كيف أجريت عملية التحليل إلى العوامل؟ ( ماقيم : المقبولة ؟ وما القيم غير المقبولة؟ وضّح إجابتك. x+2 × x+2 X X x+6 60 تصميم المباني: يمثل الشكل المجاور مخطط شقة سكنية. اكتب دالة بدلالة المتغير x تمثل مساحة الشقة. إذا كانت مساحة الشقة 1366ft2، فما قيمة x؟ حلل كلَّ كثيرة حدود فيما يأتي تحليلا تاما. وإن لم يكن ذلك ممكنا فاكتب كثيرة حدود أولية: y9 - y6 – 2y6 + 2y3 + y3 - 1(62 x64x48x4 + 32x² + 16x2 - 64 (61 x6 - 3x4y2 + 3x2y4 - y6 (63) (64) حدائق حديقة مستطيلة الشكل بعداها 32ft و 40ft ، تم توسعتها لتصبح مساحتها 4.5 أمثال مساحتها الأصلية بزيادة كل من طولها وعرضها وزارة التعليم Ministry of Education الدرس 6- حل معادلات كثيرات الحدود 215114 بالمقدار نفسه. (a) ارسم شكلا يمثل الموقف. اكتب معادلة كثيرة حدود تمثل المساحة الجديدة وحلها بالتحليل إلى العوامل. ما الحل غير المقبول؟ وضّح إجابتك. مثل الدالة بيانيا.

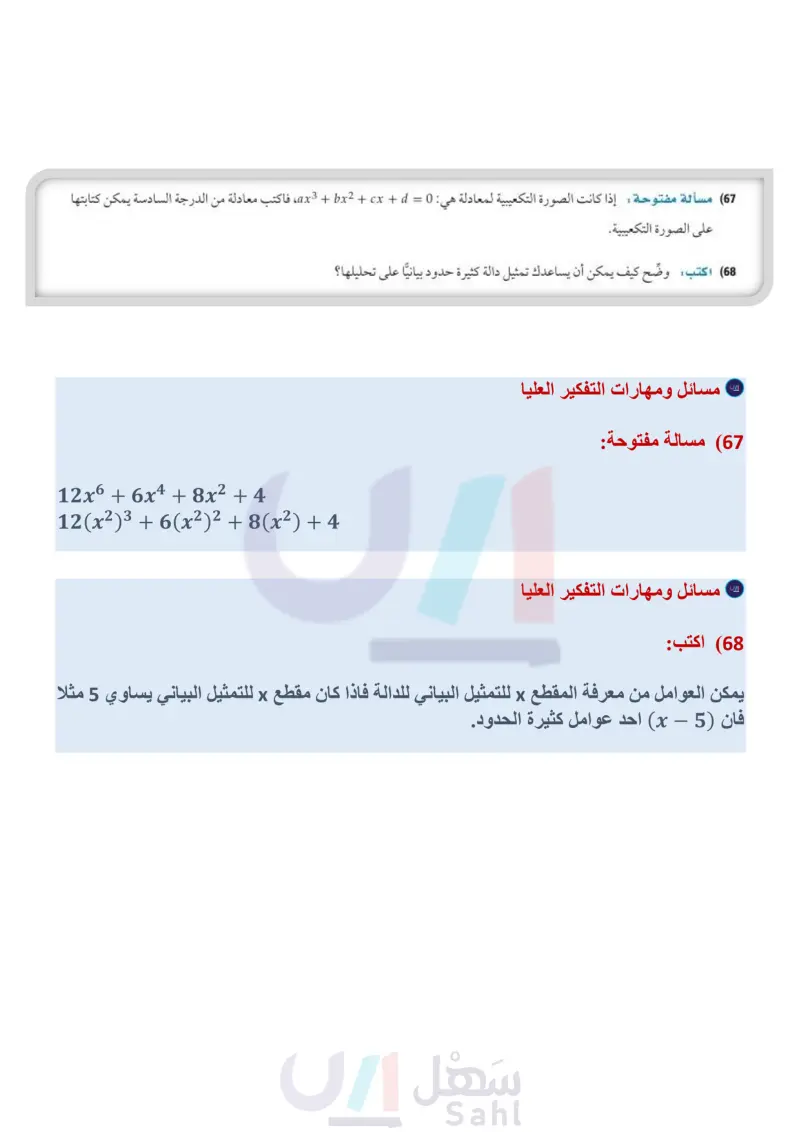
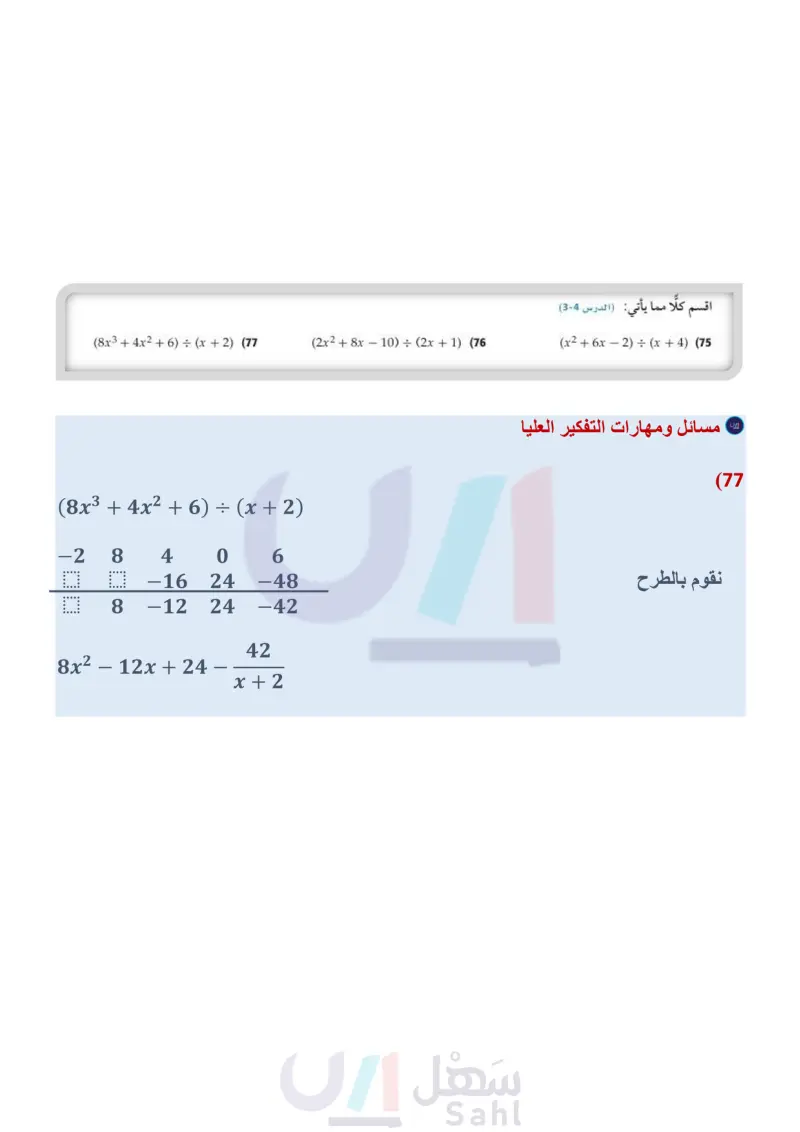
تدريب على اختبار مسائل مهارات التفكير العليا (65) تحد: حلّل المقدار 1 + 36x2n + 12x إلى عوامله. (66 تبرير أعط مثالا مضادا للعبارة : a + b = a + b2. (67) مسألة مفتوحة: إذا كانت الصورة التكعيبية لمعادلة هي : 0 = ax3 + bx2 + x + d، فاكتب معادلة من الدرجة السادسة يمكن كتابتها على الصورة التكعيبية. 68 اكتب وضّح كيف يمكن أن يساعدك تمثيل دالة كثيرة حدود بيانيًا على تحليلها؟ (69) إجابة قصيرة حل المعادلة : 0 = 27 + x3 . (70) إذا كان الفرق الموجب بين العددين k مساويًا للفرق 1 12 , 1 1 الموجب بين العددين ، فما قيمة ؟ 1 C 15 13 D 60 46-8 1 A 60 1 B 20 مراجعة تراكمية حدد الدرجة والمعامل الرئيس لكل كثيرة حدود بمتغير واحد فيما يأتي، وإذا لم تكن كثيرة حدود بمتغير واحد فاذكر السبب : (الدرس (5-3) -x4 - 3x3 + 2x6 - x7 (73 -2x5+5x4+3x² +9 (72 4x3 - 6x2 + 5x4 - 8x (71 (74) كهرباء دائرة كهربائية تتكون من جزأين موصولين على التوالي؛ معاوقة الأول 4j+ 3 أوم، ومعاوقة الثاني 6 - 2 أوم. اجمع هذين العددين المركبين لتجد المعاوقة الكلية لهذه الدائرة الدرس (1-3) وزارة التعليم Ministry of Education 2024-1446 (8x34x²+6) ÷ (x+2) (77 (2x2 + 8x - (10) ÷ (2x + 1) (76 اقسم كلًا مما يأتي : ( الدرس 4-3) (x²+6x-2) ÷ (x+4) (75 تحد: أوجد حلول كل من المعادلتين: 2 4)2=0 (78 (x² - 4)² - (x² - 4) -2 = 0 (x² + 3)² - 7(x² + 3) + 12 = 0 (79 الفصل 3 كثيرات الحدود ودوالها 152