الجذور والأصفار - رياضيات2-1 - ثاني ثانوي

رابط الدرس الرقمي www.ien.edu.sa الجذور والأصفار Roots and Zeros 3-8 فيما سبق درست استعمال الأعداد المركبة لوصف حلول المعادلات التربيعية الدرس 2 - 3 والآن : أحدد عدد جذور معادلة كثيرة حدود وأنواعها أجد عدد الأصفار الحقيقية الموجبة والسالبة والأصفار التخيلية للدالة. أكتب دالة كثيرة حدود بأقل درجة ممكنة بمعرفة أصفارها. المفردات: النظرية الأساسية في الجبر Fundamental Theorm of Algebra لماذا؟ يستعمل مدير الإنتاج في مصنع الدالة: g(x) = 1.384x4 -0.003x3 + 0.28x² - 0.078x + 1.365 لتقدير معدل تكلفة إنتاج القطعة الواحدة على مدى عدة سنوات، حيث x عدد السنوات منذ 1410هـ. ولكي تجد العام الذي يبلغ فيه معدل تكلفة إنتاج قطعة واحدة قيمة معينة، يمكنك استعمال جذور معادلة كثيرة الحدود المرتبطة بالدالة. أنواع الجذور تعلمت سابقًا أن صفر دالة مثل (f(x يمكن أن يكون أية قيمة مثل ، حيث 0 = (c). وعند تمثيل الدالة بيانيا تكون أصفارها الحقيقية هي مقاطع المحور x. ملخص المفهوم D = 6 O الأصفار، والعوامل، والجذور، والمقاطع التعبير اللفظي : إذا كانت + x) = anxn + ... + a) دالة كثيرة حدود، x a مثال : فإن العبارات الآتية متكافئة : • C صفر للدالة (x). C جذر أو حل للمعادلة 0 = (P(x. . X - C عامل من عوامل كثيرة الحدود (P(x أضف إلى مطويتك إذا كان C عددًا حقيقيًّا، فإن (0) هي نقطة تقاطع تمثيل الدالة (P(x مع المحور x . افترض أن دالة كثيرة الحدود هي: 12 + P(x) = x4 + 2x3 - 7x2 - 8x. -3, -2, 1, 2:00 هي: فإن أصفار هذه الدالة وجذور المعادلة 0 = 12 + x4 + 2x3 – 7x2 – 8x -3, -2, 1, 2:00 −2,1, هي: وعوامل كثيرة الحدود 12 + x4 + 2x3 – 7x2 - 8x (x+3), (x+2), (x − 1), (x − 2): - ونقاط تقاطع التمثيل البياني للدالة (( مع المحور x 4 P(x) A 12 -8 -4 O -4 .(−3, 0), (−2, 0), (1, 0), (2, 0) لا عند حل معادلة كثيرة حدود درجتها أكبر من صفر من الممكن أن يكون لها جذر حقيقي واحد أو أكثر، وقد يوجد جذور حقيقية (أي أن الجذور أعداد تخيلية). وبما أن الأعداد الحقيقية والتخيلية جميعها تنتمي إلى مجموعة الأعداد المركبة، يمكن القول إن أية معادلة كثيرة حدود درجتها أكبر من الصفر لها جذر واحد مركب على الأقل، وهذه هي النظرية الأساسية في الجبر. مفهوم أساسي النظرية الأساسية في الجبر أضف إلى مطويتك كل معادلة كثيرة حدود درجتها أكبر من صفر لها جذر واحد على الأقل ينتمي إلى مجموعة الأعداد المركبة. وزارة التعليم Ministry of Education 2024-1446 الفصل 3 كثيرات الحدود ودوالها 160

إرشادات للدراسة الجذور المكررة يمكن أن يكون لمعادلات كثيرات الحدود جذر مکرر مرتين أو ثلاث أو أربع مرات وهكذا. مثال 1 تحديد عدد الجذور وأنواعها حُلَّ كلَّ معادلة مما يأتي، واذكر عدد جذورها، ونوعها : x 2 + 6x + 9 = 0 a | f(x) = x2 + 6x + 9 8 f(x) x 2 + 6x + 9 = 0 (x + 3)2 = 0 x + 3 = 0 x = -3 المعادلة الأصلية حلل إلى العوامل خُذ الجذر التربيعي لكلا الطرفين أوجد قيمة x وبما أن العامل (3) مكرر مرتين في تحليل كثيرة الحدود، فإن 3- جذر مكرر مرتين. أي للمعادلة جذر حقيقي واحد مكرر مرتين هو 3- x oo + -8 -4 -8 4 تحقق بما أن التمثيل البياني للدالة يمس المحور x عندما 3 = x فإن 3- جذر مكرر مرتين. ۷ x3 + 25x = 0 b x3+25x = 0 0 = x أو x (x²+25)=0 x2 + 25 = 0 x2 = 25 x = +V-25 = 5i المعادلة الأصلية حلل إلى العوامل خاصية الضرب الصفري اطرح 25 من كلا الطرفين خاصية الجذر التربيعي، ثم التبسيط للمعادلة ثلاثة جذور : جذر حقيقي واحد هو 0 وجذران تخیلیان هما 51 ,5 . تحقق بما أن التمثيل البياني للدالة يقطع المحور x عندما 0 = x ، فإن للمعادلة جذرًا حقيقيًّا واحدًا هو 0. ✓ تحقق من فهمك |f(x) = x³ + 25x f(x) 800 4 8 x -400- -8 -400 --800 3x3 - x2 + 9x - 3 = 0 (IC x4 – 16 = 0 (1B x3 + 2x = 0 (1A اختبر حَلَّ كلّ معادلة في المثال ،1، ولاحظ أن عدد حلول كل معادلة يساوي درجة كثيرة الحدود. والنتيجة الآتية للنظرية الأساسية في الجبر تصف العلاقة بين درجة معادلة كثيرة الحدود وعدد جذورها. مفهوم أساسي نتيجة للنظرية الأساسية في الجبر أضف إلى مطويتك التعبير اللفظي: يكون لمعادلة كثيرة الحدود من الدرجة n العدد n فقط من الجذور المركبة بما في ذلك الجذور المكررة. مثال: 0 = 6 + x3 + 2x2 3 جذور -2x5 – 3x2 + 8 = 0 4x4 – 3x3 + 5x - 6 = 0 4 جذور 5 جذور وبالمثل دالة كثيرة الحدود من الدرجة n لها فقط العدد n من الأصفار المركبة وقد اكتشف العالم الفرنسي ديكارت علاقة بين إشارات معاملات دالة كثيرة الحدود وعدد الأصفار الحقيقية. وزارة التعليم Ministry of Education الدرس - الجذور والأصفار 216114

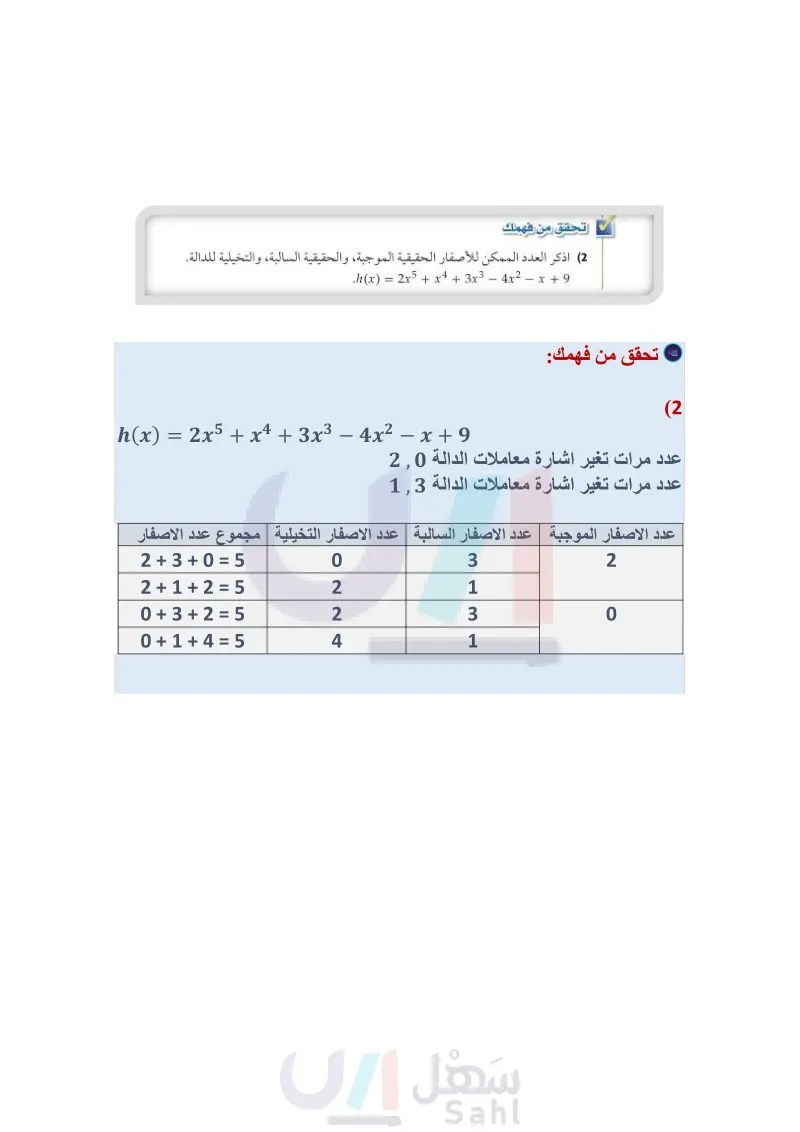
تاريخ الرياضيات رينيه ديكارت (1650 - 1596م )، فيلسوف، ورياضي، وفيزيائي فرنسي، يلقب بـ أبو الفلسفة 115 " الحديثة . له تأثير واضح في علم الرياضيات؛ فقد اخترع نظامًا رياضيًا شكّل أساس الهندسة التحليلية سمي باسمه وهو نظام الإحداثيات الديكارتية. مفهوم أساسي قانون ديكارت للإشارات = أضف إلى مطويتك إذا كانت x + a + ... + x nxn دالة كثيرة حدود معاملات حدودها أعداد حقيقية، فإن : عدد الأصفار الحقيقية الموجبة للدالة (X) يساوي عدد مرات تغير إشارة معاملات حدود الدالة (x) ، أو أقل منه بعدد زوجي. • عدد الأصفار الحقيقية السالبة للدالة (x) يساوي عدد مرات تغير إشارة معاملات حدود الدالة (P(x ، أو أقل منه بعدد زوجي. مثال 2 إيجاد عدد الأصفار الحقيقية الموجبة والسالبة والأصفار التخيلية لدالة اذكر العدد الممكن للأصفار الحقيقية الموجبة، والحقيقية السالبة، والتخيلية للدالة .f(x) = x6 + 3x5 - 4x4 - 6x3 + x2 - 8 x + 5 بما أن درجة الدالة (f(x تساوي 6 ، فإن لها 6 أصفار حقيقية أو تخيلية أو كليهما. استعمل قانون ديكارت للإشارات لتحديد العدد الممكن للأصفار الحقيقية ونوعها. احسب عدد مرات تغير إشارة معاملات الدالة (f(x . f(x) = = x6 + 3x5 4x4 - + 6x3 x2 - + 8x 5 + نعم نعم + + نعم نعم + ++ نجد أن هناك 4 تغيرات في إشارة المعاملات، لذا فإن عدد الأصفار الحقيقية الموجبة سيكون: 4 أو 2 أو 0. احسب عدد مرات تغير إشارة معاملات الدالة (f(x تنبيه أصفار الدوال لن تناقش الحالة التي يكون فيها الحد الثابت f(x) = (-x)6 + 3(-x)5 - 4(-x)4 6(-x)³ + (-x)² = x6 3x5 - 6x3 + 4x4 + + x2 8(-x)+ 8x 5 + 5 لا ++ ++ + ++ نعم نعم + مساويًا للصفر في هذا الدرس. نجد أن هناك تغيرين في إشارة المعاملات، لذا فإن عدد الأصفار الحقيقية السالبة سيكون: 2 أو 0. أنشئ جدولاً يبين عدد الجذور الحقيقية والتخيلية الممكنة. 162 عدد الأصفار عدد الأصفار عدد الأصفار التخيلية يساوي العدد 6 مطروحًا منه الحقيقية الموجبة الحقيقية السالبة مجموع عدد الأصفار الحقيقية 0 2 4 2 0 2 2 2 4 0 4 2 0 6 0 تحقق من فهمك (2) اذكر العدد الممكن للأصفار الحقيقية الموجبة، والحقيقية السالبة، والتخيلية للدالة. h(x) = 2x5 + x4 + 3x3 - 4x2 - x + 9 تعلمت سابقًا أن حاصل ضرب العددين المركبين المترافقين هو عدد حقيقي دائمًا، ومن الجدير بالذكر أن الجذور المركبة تكون في أزواج مترافقة. فمثلا إذا علمت أن أحد جذري المعادلة 0 = 52 + x2 – 8x هو 6i + 4، فإنك أن الجذر الآخر هو 6i – 4. وزارة التعليم تستنتج الفصل 3 كثيرات الحدود ودوالها Ministry of Education 2024-1446

وينطبق هذا الأمر على أصفار دوال كثيرات الحدود أيضًا. فإذا كان العدد المركب صفرًا لدالة كثيرة حدود معاملات حدودها أعداد حقيقية، فإن مرافقه أيضًا صفر لدالة كثيرة الحدود. مفهوم أساسي نظرية الأصفار المركبة المترافقة أضف إلى ' مطويتك التعبير اللفظي : إذا كان عددين حقيقيين ، و كان a b صفرًا لدالة كثيرة حدود معاملات حدودها أعداد حقيقية فإن a - bi صفر للدالة أيضًا. مثال : إذا كان 4 + 3 صفرًا للدالة 50 + x) = x3 - 4x2 + 13x)، فإن 4 - 3 صفر للدالة أيضًا. إرشادات للدراسة استعمال الأصفار لكتابة الدالة إن أي دالة على الصورة ، f(x) = a(x3 - 9x2 +16x +26) ( حيث 1 عدد صحيح لا لا يساوي الصفر)، تحقق المعطيات الواردة في المثال 3 ولكن اعتبر أن 1 = a للتسهيل فقط. عندما تعطى جميع أصفار دالة كثيرة حدود ويطلب إليك تحديد الدالة، حوّل الأصفار إلى عوامل، ثم اضرب جميع العوامل بعضها في بعض ؛ لتحصل على دالة كثيرة الحدود المطلوبة. مثال 3 استعمال الأصفار لكتابة دالة كثيرة حدود اكتب دالة كثيرة حدود درجتها أقل ما يمكن ومعاملات حدودها أعداد ،صحيحة إذا كان العددان 1 - 1 من أصفارها . افهم المعطيات العددان - - -1،5 من أصفار كثيرة حدود. – - المطلوب : كتابة دالة كثيرة حدود درجتها أقل ما يمكن ومعاملات حدودها أعداد صحيحة، والعددان - - 15 - من أصفارها. 1 خطط بما أن i - 5 صفر للدالة، فإن i + 5 أيضًا صفر للدالة بحسب نظرية الأصفار المركبة المترافقة. - - - لذا فإن , عوامل لكثيرة الحدود. حل اكتب المعادلة كثيرة الحدود على صورة حاصل ضرب عواملها. P(x) = (x + 1)[x − (5 – i)][x − (5 + i)] - - اضرب العوامل لتحصل على دالة كثيرة الحدود. – P(x) = (x + 1) [x - (5 - i)][x - (5 + i)] = (x + 1) [(x-5) + i][(x − 5) — i] - - = (x + 1) [(x-5)² - 12] = (x + 1) [(x2 – 10x + 25 - (1)] - 10x + 26 = (x + 1) (x2 – 10x + 26) - = x3 - 10x2 + 26x + x2 - = x3 - 9x2 + 16x + 26 اكتب الدالة أعد تجميع الحدود الفرق بين مربعين أوجد مربع الحدين بسط اضرب اجمع الحدود المتشابهة تحقق بما أن هناك 3 أصفار فإن دالة كثيرة الحدود ستكون من الدرجة الثالثة، ولذا فإن 26 + P(x) = x3 - 9x2 + 16x دالة كثيرة حدود درجتها أقل ما يمكن، ومعاملات حدودها أعداد صحيحة، وأصفارها هي: 1 - 15 . تحقق من فهمك ' (3) اكتب دالة كثيرة حدود درجتها أقل ما يمكن ومعاملات حدودها أعداد صحيحة، إذا كان العددان 2i +1 من أصفارها. ― وزارة التعليم Ministry of Education. الدرس - الجذور والأصفار 216314

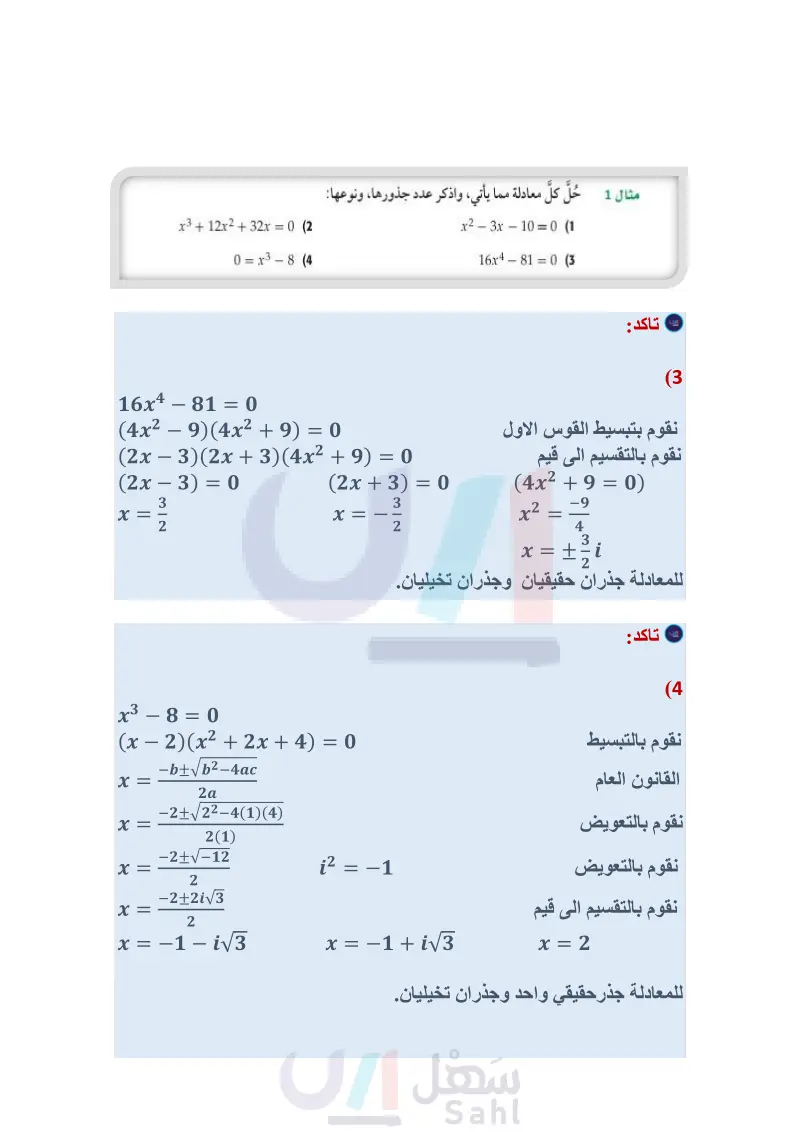
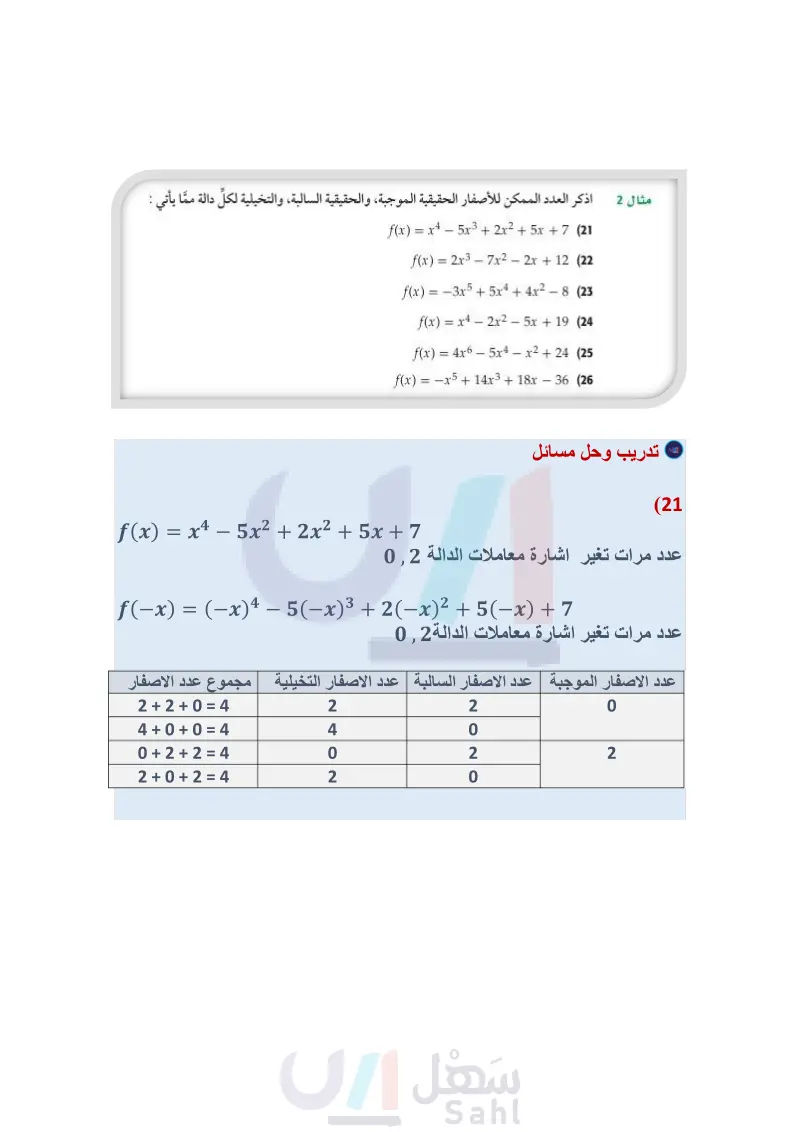
x3+12x2+32x x3 + 12x2 + 32x = 0 (2 0 = x3 - 8 (4) مثال 1 حُلَّ كلّ معادلة مما يأتي، واذكر عدد جذورها، ونوعها: x2 - 3x - 10 = 0 (1 16x4810 (3 اذكر العدد الممكن للأصفار الحقيقية الموجبة والحقيقية السالبة، والتخيلية لكل دالة مما يأتي : مثال 2 f(x) = x3 - 2x2 + 2x - 6 (5 f(x) = 6x4 + 4x3 - x2 - 5x - 7 (6) f(x) = 3x5 - 8x3 + 2x - 4 (7 f(x) = -2x4 - 3x3 - 2x - 5 (8 - اكتب دالة كثيرة حدود درجتها أقل ما يمكن ومعاملات حدودها أعداد صحيحة، إذا كانت الأعداد المعطاة مثال 3 كل مما يأتي من أصفارها : وزارة التعليم Ministry of Education 2024-1446 3,-1,1,2 (10 -4,4+i (12 4,-1,6 (9 -2,5,-3i (11 تأكد تدرب وحل المسائل حُلَّ كلَّ معادلة مما يأتي، واذكر عدد جذورها، ونوعها: مثال 1 2x2 - 5x + 14 = 0 (14 +14 = 8x3 - 27 = 0 (16 x3 - 6x2 + 7x = 0 (18 x5 + 2x3 + x = 0 (20 4x2 + 1 = 0 (13 -3x2 - 5x + 8 = 0 (15 16x4 6250 (17 x5 – 8x3 + 16x = 0 (19 اذكر العدد الممكن للأصفار الحقيقية الموجبة، والحقيقية السالبة، والتخيلية لكلّ دالة مما يأتي : مثال 2 f(x) = x4 - 5x3 + 2x2 + 5x + 7 (21 f(x) = 2x3 - 7x2 - 2x + 12 (22) f(x) = - 3x5 + 5x4 + 4x2 - 8 (23) f(x) = x4 - 2x2 - 5x + 19 (24 f(x) = 4x6 – 5x4 - x2 + 24 (25 f(x) = -x5 + 14x3 + 18x - 36 (26 الفصل 3 كثيرات الحدود ودوالها 164

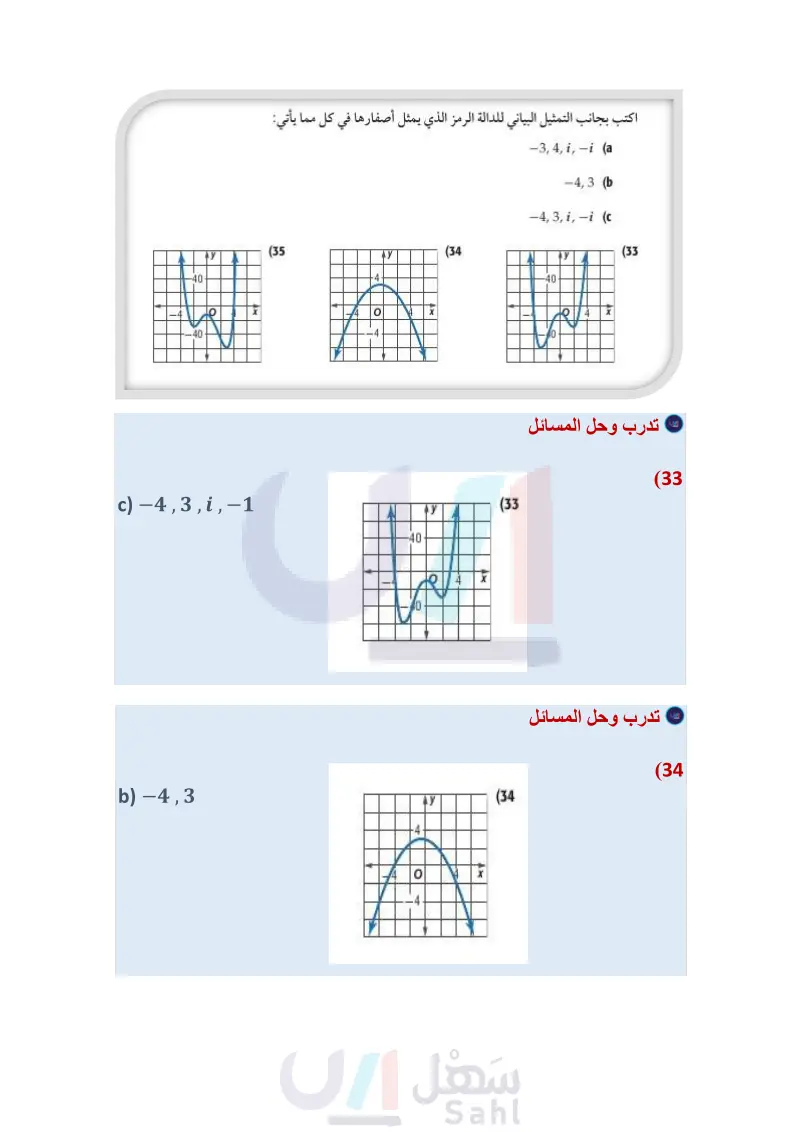
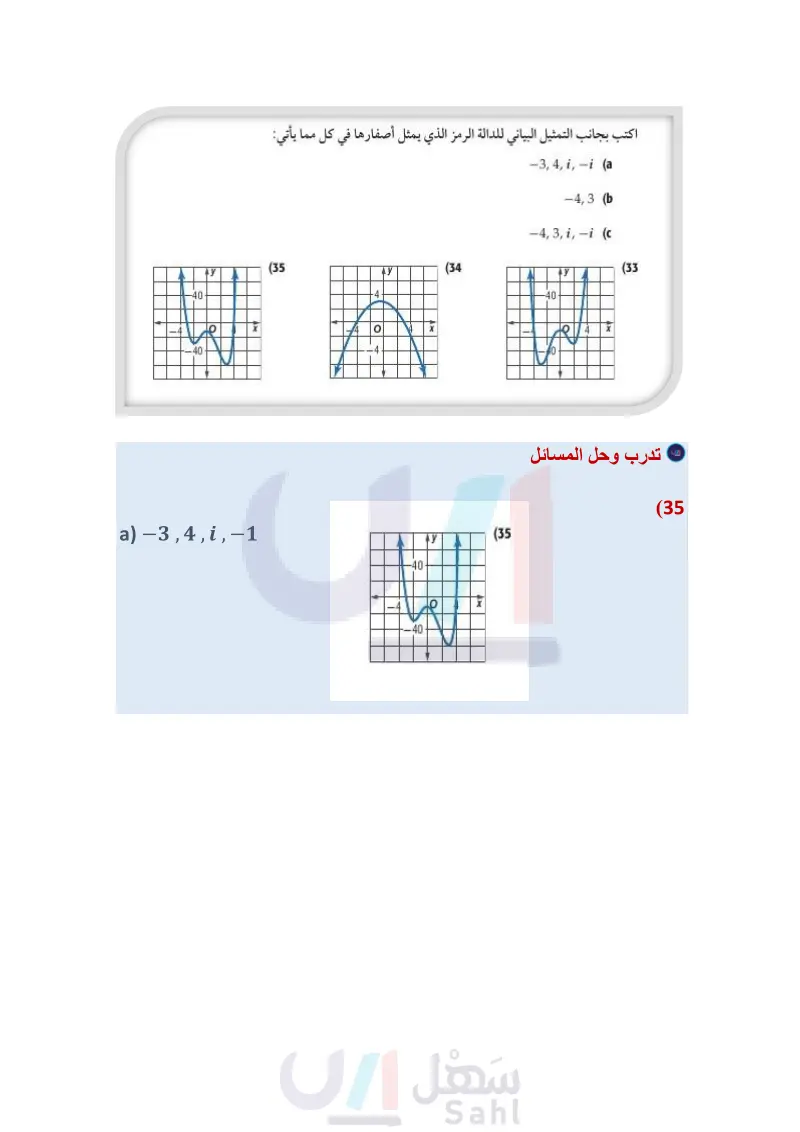
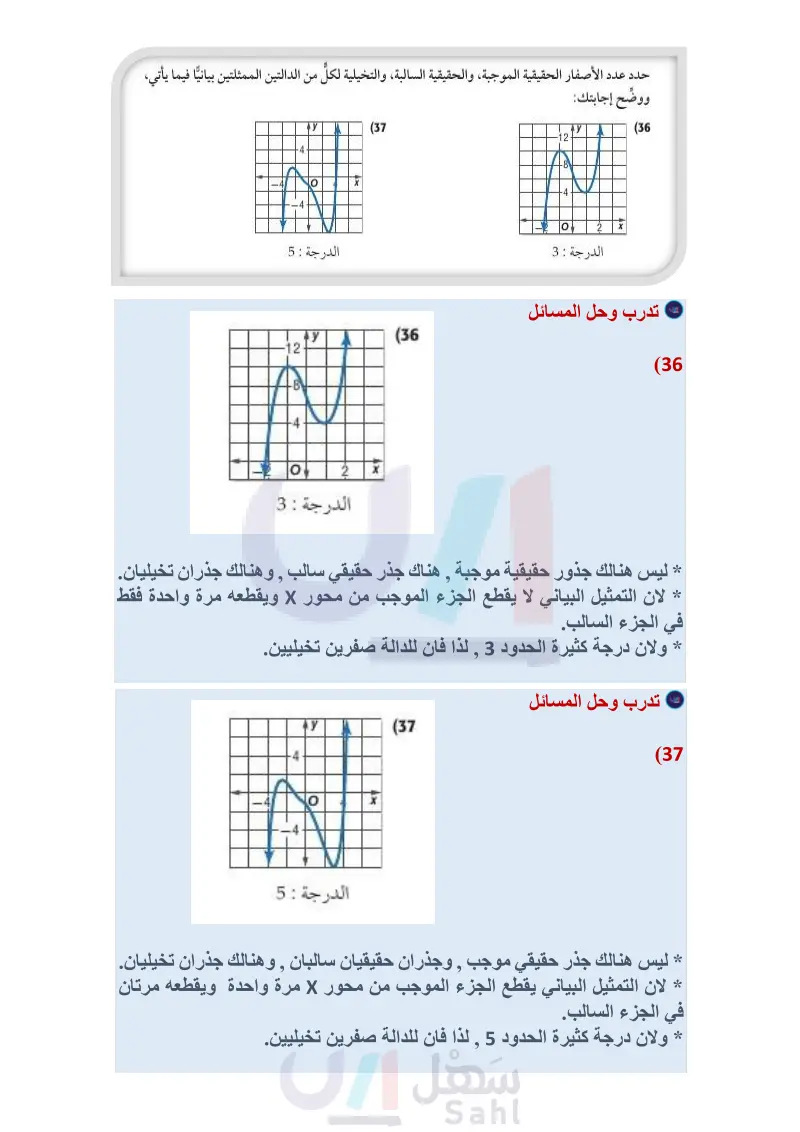
مثال 3 اكتب دالة كثيرة حدود درجتها أقل ما يمكن ومعاملات حدودها أعداد صحيحة، إذا كانت الأعداد المعطاة في كل مما يأتي من أصفارها : -40 46 АУ -4 -40- 5,-2,-1 (27 -4,-3,5 (28 -1,-1,2i (29 -3,1,-3i (30 0,-5,3i (31 -2, -3,4-3i (32 اكتب بجانب التمثيل البياني للدالة الرمز الذي يمثل أصفارها في كل مما يأتي: -3, 4, i, -i (a -4,3 (b -4, 3, i, -i (c (35 АУ (34 У (33 4 -40 40 X 4 X -4 X 4 40 حدد عدد الأصفار الحقيقية الموجبة، والحقيقية السالبة، والتخيلية لكلِّ من الدالتين الممثلتين بيانيا فيما يأتي، ووضح إجابتك: وزارة التعليم Ministry of Education -4 У (37 الدرجة : 5 الدرس - الجذور والأصفار 216514 X МУ (36 12- 8 st 이 2 X الدرجة : 3

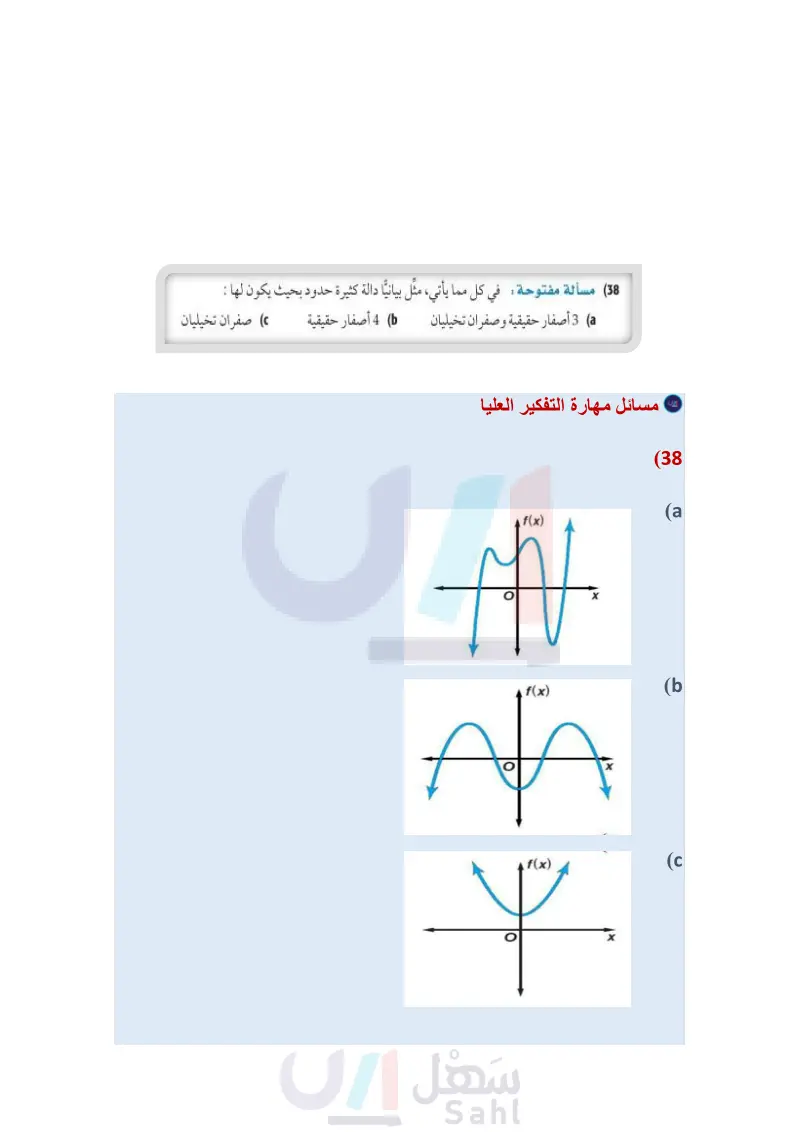
مسائل مهارات التفكير العليا (38) مسألة مفتوحة في كل مما يأتي، مثل بيانيا دالة كثيرة حدود بحيث يكون لها : ( 3 أصفار حقيقية وصفران تخيليان b) 4 أصفار حقيقية : صفران تخیلیان (39) تحد اكتب معادلة على صورة حاصل ضرب عوامل دالة كثيرة حدود من الدرجة الخامسة، لها صفران تخيليان، وصفر غير صحيح، وصفران غير نسبيين، ووضّح إجابتك . (40) حدد أي المعادلات الآتية تختلف عن الأخريات، ووضّح إجابتك: r3 + 1 = 0 r4 + 1 = 0 r2 - 1 = 0 r3-8=0 (41 تبرير اكتب مثالاً مضادا لكل عبارة فيما يأتي: (a (b جميع دوال كثيرات الحدود التي تزيد درجتها على 2 لها على الأقل صفر حقيقي سالب. جميع دوال كثيرات الحدود التي تزيد درجتها على 2 لها على الأقل صفر حقيقي موجب. (42) اكتب وضّح لزميلك كيف تستعمل قانون ديكارت للإشارات لتحديد عدد الأصفار الحقيقية الموجبة والسالبة الممكنة لدالة كثيرة الحدود 12 - f(x) = x4 - 2x3 + 6x 2 + x وزارة التعليم Ministry of Education 2024-1446 --12 4 x تدريب على اختبار (43) استعمل التمثيل البياني للدالة 4 - f(x) = x5 + x - 3x3 - 3x2 - 4x، وحدّد أيًا مما يأتي لا يعد عاملاً لكثيرة الحدود 4 - x5 + x4 - 3x3 - 3x2 - 4x؟ x + 2 C x + 1 D x - 2 A x - 1 B مراجعة تراكمية أوجد (4), (8) لكل دالة مما يأتي مستعملا التعويض التركيبي (الدرس (7-3) f(x) = 4x3 + 6x2 - 3x + 2 (44 f(x) = 5x4 - 2x3 + 4x2 - 6x (45) f(x) = 2x5 - 3x3 + x2 - 4 (46) حلّل كلَّ كثيرة حدود مما يأتي تحليلا تامًا، وإن لم يكن ذلك ممكنا فاكتب كثيرة حدود أولية (الدرس 6-3) x6-46 (47 4x2y + 8xy + 16y - 3x2z - 6xz - 122 (48) 5a3 – 30a2 + 40a + 2a2b - 12ab + 166 (49 الفصل 3 كثيرات الحدود ودوالها 166

الفصل 3 دليل الدراسة والمراجعة • ملخص الفصل المفاهيم الأساسية الأعداد المركبة الدرس (1-3) i • هي الوحدة التخيلية، 1- = 12 ، 1-i = V العدد المركب هو أيُّ عدد يمكن كتابته على الصورة a + bi ؛ حيث a و b عددان حقيقيان ويسمى a الجزء الحقيقي، وط الجزء التخيلي. • القانون العام والمميز (الدرس (2-3) القانون العام لحل المعادلة التربيعية: x = -b + Vb2 -4ac 2a المفردات الأساسية الوحدة التخيلية (108) دالة كثيرة الحدود (139) العد التخيلي البحت (108) العدد المركب (109) المركبان المترافقان (111) القانون العام (115) دالة القوة (139) سلوك طرفي التمثيل البياني (140) صفر الدالة (140) كثيرة الحدود الأولية (145) المميز (118) التبسيط (125) الصورة التربيعية (148) نظرية الباقي (154) درجة كثيرة الحدود (127) التعويض التركيبي (154) القسمة التركيبية (132) نظرية العوامل (156) • . • • • العمليات على كثيرات الحدود الدرسان 4-3-13 عند الجمع أو الطرح: أجمع الحدود المتشابهة. عند الضرب: أستعمل خاصية التوزيع. عند القسمة : أستعمل القسمة الطويلة أو التركيبية. دوال كثيرات الحدود الدرس (5-3) تعرّف دالة كثيرة الحدود بأنها دالة متصلة يمكن وصفها بمعادلة كثيرة حدود بمتغير واحد. حل معادلات كثيرات الحدود الدرس (36) يمكن تحليل كثيرة الحدود باستعمال العامل المشترك الأكبر أو تجميع الحدود، أو بإحدى طرائق تحليل الدالة التربيعية. نظريتا الباقي والعوامل (الدرس (7-3) نظرية الباقي : إذا قسمت كثيرة حدود (P(x على x - r ، فإن الباقي ثابت ويساوي (r) . . نظرية العوامل: تكون ثنائية الحد x – a عاملًا من عوامل كثيرة الحدود (f(x إذا وفقط إذا كان 0 = (f (a . الجذور، والأصفار (الدرس (38) . نظرية الأصفار المركبة المترافقة إذا كان a + bi صفرًا للدالة، فإن a - bi صفر للدالة أيضًا. المطويات منظم أفكار تأكد أن المفاهيم الأساسية مدونة في مطويتك. الأعداد المركبة كثيرات دوال الحدود كثيرات الحدود كثيرات الحدود معادلات كثيرة حدود بمتغير واحد (138) النظرية الأساسية في الجبر (160) المعامل الرئيس (136) اختبر مفرداتك بين ما إذا كانت كل عبارة فيما يأتي صحيحة أم خاطئة. وإذا كانت خاطئة فاستبدل ما تحته خط لتصبح العبارة صحيحة: 1) العدد 61 تخيلي بحت (2) يسمى القانون -b+Vb2-4ac 2a = x بالمميز (3) يُسمى معامل الحد الأول في كثيرة الحدود المكتوبة بالصيغة القياسية المعامل الرئيس. (4 تُسمى كثيرة الحدود التي لا يمكن تحليلها كثيرة حدود بمتغير واحد. دالة متصلة يمكن وصفها بمعادلة كثيرة (5 دالة كثيرة الحدود هي حدود بمتغير واحد. (6 تبسيط عبارات تتضمن قوى، يعني إعادة كتابتها دون أقواس أو أسس سالبة. 7) القسمة التركيبية هي طريقة مختصرة لقسمة كثيرة حدود على ثنائية (8 حد. - 8) 0 = 8 - x32 + 3x3) هي دالة قوة. وزارة التعليم Ministry of Education الفصل 3 دليل الدراسة والمراجعة 216714

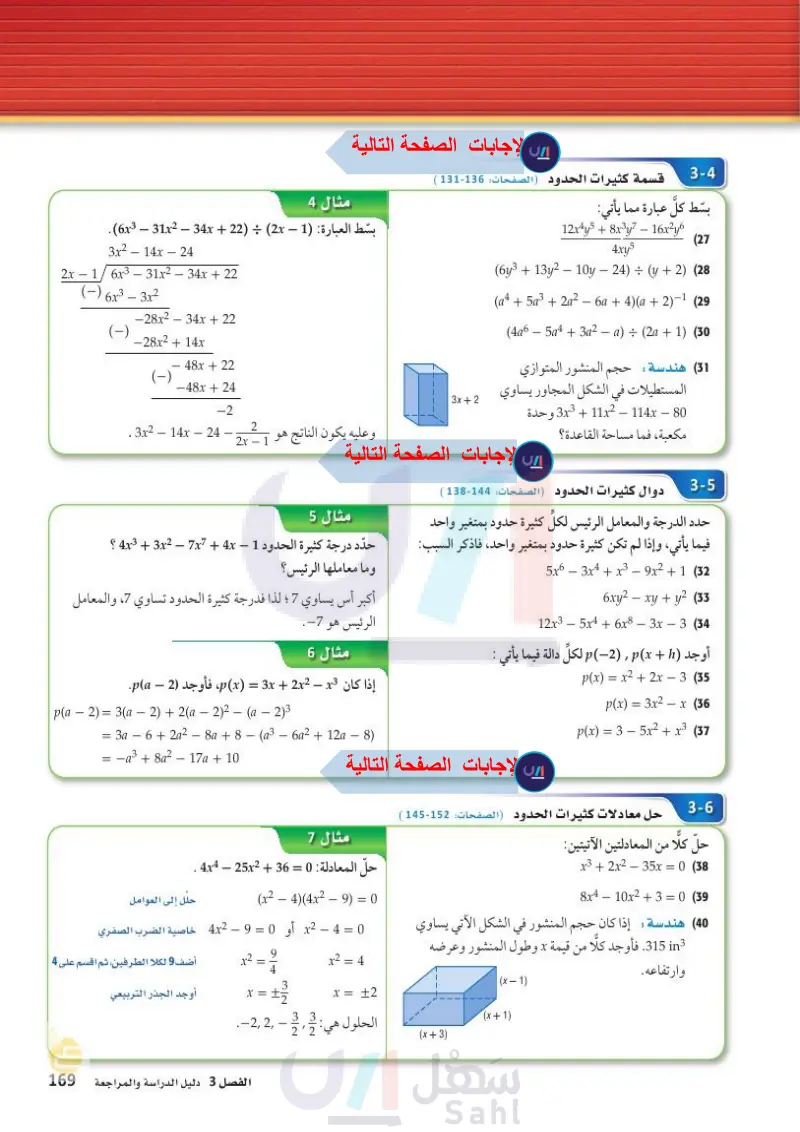
المعادلة الأصلية اطرح 12 من كلا الطرفين اقسم كلا الطرفين على 3 خاصية الجذر التربيعي √√-4=√√4.√√-1 القانون العام a=1, b=-4, c = -45 بسط اكتب على صورة معادلتين بسط مثال 1 حل المعادلة : 0 = 12 + 3x2 3x²+12=0 3x2 = -12 x2 = -4 x = +V-4 x = + 2i دليل الدراسة و المراجعة الفصل 3 مراجعة الدروس 3-1 الأعداد المركبة (الصفحات: 116-110) بسط كلا مما يأتي: (2 − i) + (13+ 4i) (10 (6+5i) (32i) (12 -8 (9 (6+2i) – (4 – 3i) (11 (13) كهرباء : تبلغ المعاوقة في أحد أجزاء دائرة كهربائية 2i + 3+ أوم، وفي الجزء الآخر منها 36 – 4 أوم. اجمع هذين العددين لتجد المعاوقة الكلية في الدائرة الكهربائية. حل كلًا من المعادلات الآتية: 4x² +10 (15 2x²+500 (14 x = = مثال 2 حل المعادلة 0 = 45 - x2 - 4x a = 1, b = -4, c = -45 -b + Vb2 – 4ac 2a -(-4)±√√(-4)2 -4)² - 4(1)(−45) 3-2 القانون العام والمميز الصفحات: 124-117 ) أجب عن الفروع ac لكلّ معادلة تربيعية فيما يأتي: a) أوجد قيمة المميز. ) أوجد عدد الجذور المختلفة، وحدد أنواعها. C حل المعادلة باستعمال القانون العام. x2 + 4x - 32 = 0 (17 4x2 - 4x + 1 = 0 (19 x2 - 10x + 25 = 0 (16 2x2 + 3x - 18 = 0 (18 || 2(1) 4 ± 14 2 x = 4 + 14 2 = 9 . (20) فيزياء: قذف محمد كرة رأسيا إلى أعلى بسرعة ابتدائية مقدارها 40ft s. إذا علمت أن ارتفاع الكرة عن الأرض (h) بالأقدام يعطى بالمعادلة 5 + h = 16t2 + 40t ، ― حيث الزمن بالثواني، فأوجد الزمن اللازم لتصل الكرة إلى الأرض. x = 4 - 14 2 = -5 ' إذن الحلَّان هما : 59 مثال 3 بسط كلا مما يأتي: (-4a3b5)(5ab3) (a 3-3 العمليات على كثيرات الحدود الصفحات: 132-127) بسط كلا مما يأتي مفترضًا أن أيا من المتغيرات لا يساوي صفرا: 14x4y (21 2x³y5 3t(tn - 5) (22 اضرب القوى بسط (-4a3b5)(5ab³) -4a3b5) (5ab3) = (4)(5)a3 + 15 + 3 = -20a4b8 ...... 2x 2 + 3x - 8) + (3x2 - 5x - 7) (b (2x2 + 3x – 8) + (3x2 - 5x - 7) = (2x² + 3x²) + (3x-5x) + [-8+ (-7)] 15 - 5x2 - 2x =وزارة التعليم (4r² + 3r − 1) − (3r² – 5r + 4) (23 - (x4)3 (24 (m + p)(m2 - 2mp + p2) (25 3b(2b 1) + 2b(b + 3) (26 ― Ministry of Education 2024-1446 الفصل 3 كثيرات الحدود ودوالها 168

3-4 قسمة كثيرات الحدود الصفحات: 138-133 ) بسط كلَّ عبارة مما يأتي: 12x4y5 + 8x³y7 — 16x²y6 4xy5 (27 (6y3 + 13y2 - 10y - 24) : (y + 2) (28 (a45a32a2 - 6a+ 4)(a + 2)-1 (29 (4a6 – 5a4 + 3a2 - a) : (2a + 1) (30 المنشور المتوازي (31) هندسة حجم المستطيلات في الشكل المجاور يساوي 80 - 3x3 + 11x2 - 114x وحدة مكعبة، فما مساحة القاعدة؟ 3-5 3x+2 دوال كثيرات الحدود الصفحات: 146-140 ) مثال 4 بسط العبارة (1) - 6x3 - 31x2 - 34x + (22) ÷ (2x) . : 3x2 14x 24 - 2x - 1 / 6x3 – 31x2 - 34x + 22 6x³-3x² -28x2 – 34x + 22 -28x2 + 14x - - 48x + 22 (-) -48x+24 -2 2 . 3x2 – 14x - 24 وعليه يكون الناتج هو 1 - 2x - حدد الدرجة والمعامل الرئيس لكلّ كثيرة حدود بمتغير واحد مثال 5 حدد درجة كثيرة الحدود 1 - 4x3 + 3x2 - 7x7 + 4x ؟ فيما يأتي، وإذا لم تكن كثيرة حدود بمتغير واحد، فاذكر السبب: 5x6 - 3x4 +x³ - 9x² +1 (32 6xy2 - xy + y2 (33) 12x3 – 5x4 + 6x8 - 3x – 3 (34 أوجد ) (2)p لكل دالة فيما يأتي : p(x) = x2 + 2x - 3 (35) p(x) = 3x2 - x (36) p(x) = 3 – 5x2 + x3 (37 وما معاملها الرئيس؟ أكبر أس يساوي 7 ؛ لذا فدرجة كثيرة الحدود تساوي 7، والمعامل الرئيس هو 7-. مثال 6 إذا كان 3 - 22 + p(x) = 3x، فأوجد (2) - pa. - p(a− 2) = 3(a – 2) + 2(a− 2)² - (a – 2)³ - = 3a - 6 + 22 - 8a + 8 - (3 - 6a2 + 12a - (8) = -3 + 82 - 17 + 10 3-6 حل معادلات كثيرات الحدود الصفحات: 154-147) حلّ كلا من المعادلتين الآتيتين: x3 + 2x2 - 35x = 0 (38 8x4 _ 10x2 + 3 = 0 (39 مثال 7 حل المعادلة : 0 = 36 + 4x4 – 25x2 (x24)(4x29) = 0 حلل إلى العوامل 0 = 4 - x2 أو 0 = 9 - 4x2 خاصية الضرب الصفري المنشور في الشكل الآتي يساوي (40) هندسة : إذا كان حجم لگا in3 315. فأوجد كلا من قيمة x وطول المنشور وعرضه وارتفاعه. (x-1) (x + 1) (x + 3) x x2 = 2 = 13 9 x2 = 4 x = +2 أضف 9 لكلا الطرفين، ثم اقسم على 4 أوجد الجذر التربيعى 33 الحلول هي: 1, 2,2,3 22 وزارة التعليم Ministry of Education الفصل 3 دليل الدراسة والمراجعة 216914

3-7 نظريتا الباقي والعوامل الصفحات: 161-156 ) مثال 8 أوجد (4), (2) لكلّ دالة فيما يأتي مستعملا التعويض التركيبي: حدد ما إذا كان 6 - x عاملا من عوامل كثيرة الحدود: x3 - 22 - 21x - 18 6 1 -2 -21 -18 6 24 18 1 4 3 0 f(x) = x2 - 3 (41 f(x) = x2 – 5x + 4 (42 f(x) = x3 + 4x2 - 3x + 2 (43 f(x) = 2x4 - 3x3 + 1 (44 6 - x عامل من عوامل كثيرة الحدود؛ لأن باقي قسمة كثيرة الحدود في كل مما يأتي كثيرة حدود وأحد عواملها. أوجد عواملها الأخرى عليه يساوي صفرًا. 3x320x2+23x-10, x + 5 (45 2x3 + 11x2 + 17x + 5, 2x + 5 (46 x3 + 2x2 - 23x - 60, x - 5 (47) 3-8 الجذور والأصفار (الصفحات: 168-162) اذكر العدد الممكن للأصفار الحقيقية الموجبة، والحقيقية السالبة، والتخيلية لكل دالة مما يأتي: f(x) = -2x3 + 11x2 - 3x + 2 (48 f(x) = - 4x4 - 2x3 - 12x2 - x - 23 (49) f(x) = x6 - 5x3 + x 2 + x - 6 (50 f(x) = - 25 + 4x4 + x2 - 351 - f(x) = -2x6 + 4x4 + x2 - 3x - 3 (52) مثال و اذكر العدد الممكن للأصفار الحقيقية الموجبة، والحقيقية السالبة، والتخيلية للدالة : 48 - f(x) = 3x4 + 2x3 - 22 - 26x . تتغير إشارة الدالة ( f ( x مرة واحدة؛ لذا يوجد صفر حقيقي موجب واحد. تتغير إشارة الدالة (f(x ثلاث مرات؛ لذا يوجد للدالة صفر واحد، أو ثلاثة أصفار حقيقية سالبة. الدالة ليس لها أصفار تخيلية، أو لها صفران تخيليان. وزارة التعليم Ministry of Education 2024-1446 الفصل 3 كثيرات الحدود ودوالها 170

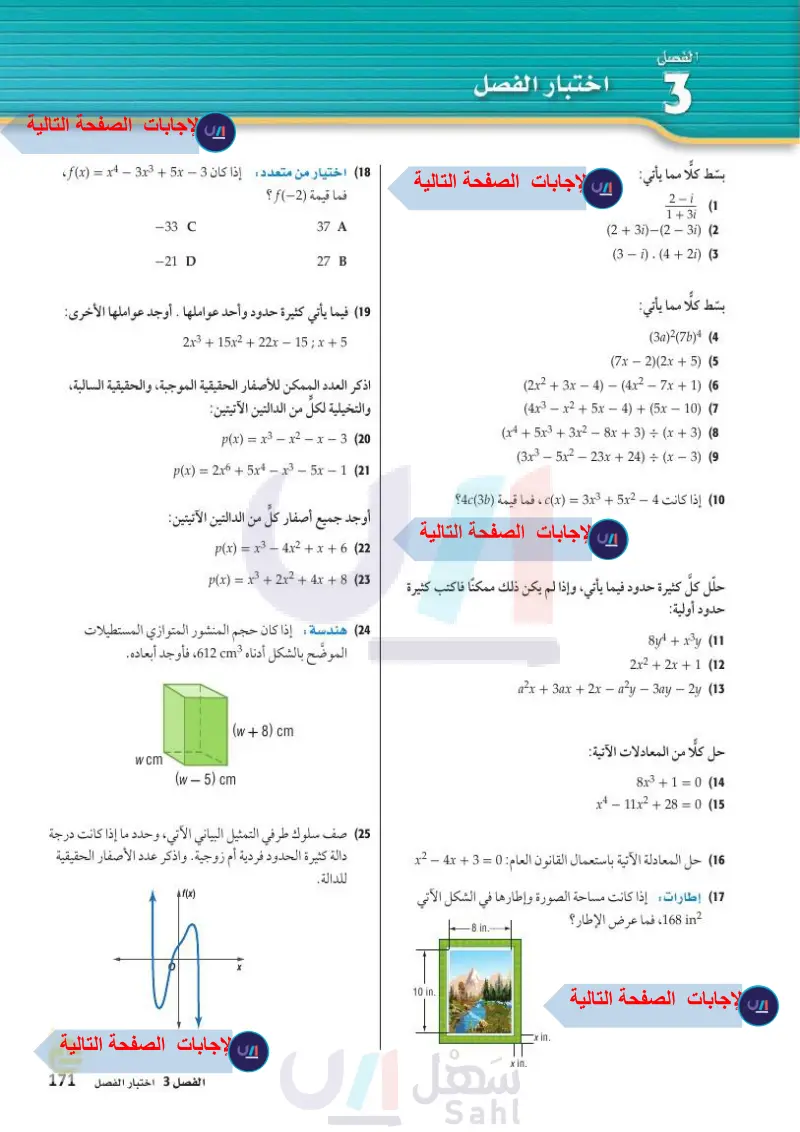
18 اختيار من متعدد : إذا كان 3 - f(x) = x4 - 3x3 + 5x ، فما قيمة (2)f ؟ -33 C -21 D 37 A 27 B 19 فيما يأتي كثيرة حدود وأحد عواملها . أوجد عواملها الأخرى: 2x3 + 15x2 + 22x - 15 ; x +5 اذكر العدد الممكن للأصفار الحقيقية الموجبة، والحقيقية السالبة والتخيلية لكل من الدالتين الآتيتين: p(x) = x3 - x2 - x - 3 (20 p(x) = 2x6 + 5x4 - x3 - 5x - 1 (21 الفصل 3 بسّط كلًا مما يأتي: اختبار الفصل 2 - i 1 + 3i (1 (231) (23i) (2 (3 −i). (4 + 2i) (3 بسط كلا مما يأتي: (3a)2(7b)4 (4 (7x2)(2x+5) (5 (2x2 + 3x - 4) - (4x2 - 7x + 1) (6) (4x3 - x2 + 5x - 4 + (5x - 10) (7 (x4 +5x3+3x² - 8x + 3) ÷ (x+3) (8 (3x3 - 5x2 - 23x + 24) ÷ (x - 3 (9 (10) إذا كانت 4 - c(x) = 3x3 + 5x2 ، فما قيمة (3)4c؟ أوجد جميع أصفار كل من الدالتين الآتيتين: حلل كلَّ كثيرة حدود فيما يأتي، وإذا لم يكن ذلك ممكنا فاكتب كثيرة حدود أولية: 8y + x³y (11 2x2 + 2x + 1 (12 a2x + 3ax + 2x - a2y - 3ay - 2y (13 p(x) = x3 - 4x2 + x + 6 (22 p(x) = x3 + 2x2 + 4x + 8 (23 (24) هندسة : إذا كان حجم المنشور المتوازي المستطيلات الموضح بالشكل أدناه cm3 612، فأوجد أبعاده. w cm (w - 5) cm (w + 8) cm حل كلا من المعادلات الآتية: 8x310 (14 x4 – 11x2 + 28 = 0 (15 (16) حل المعادلة الآتية باستعمال القانون العام : 0 = 3 + x2 - 4x 17) إطارات إذا كانت مساحة الصورة وإطارها في الشكل الآتي in2 168، فما عرض الإطار؟ -8 in.- 25) صف سلوك طرفي التمثيل البياني الآتي، وحدد ما إذا كانت درجة دالة كثيرة الحدود فردية أم زوجية. واذكر عدد الأصفار الحقيقية للدالة. f(x) وزارة التعليم Ministry of Education الفصل 3 اختبار الفصل 2171144 X 10 in. x in. x in.

الفصل 3 الإعداد للاختبارات المعيارية رسم شكل يعد رسم الشكل طريقة مفيدة في حل المسألة، فهو يعطي تصورا لكيفية الحل، لذا ارسم شكلا يمثل المسألة في ورقة مسودة أو في ورقة الإجابة (إذا سمح بذلك). استراتيجيات لرسم شكل خطوة 1 اقرأ المسألة بعناية. واسأل نفسك الأسئلة الآتية: ما المطلوب حله؟ • • ما معطيات المسألة؟ ما المجاهيل التي يُراد نمذجتها وإيجادها؟ خطوة 2 ارسم شكلًا لا وضع عليه المسميات والبيانات على أن يكون واضحًا ودقيقا ما أمكن. تشتمل المسميات التي توضع على الشكل على جميع معطيات المسألة. خطوة 3 حل المسألة. • استعمل الشكل لمساعدتك على نمذجة المسألة بمعادلة، ثم حلها. . تحقق من معقولية إجابتك. مثال 20-2 X+C (2012) - 201 (X+1) 2+ X: اقرأ المسألة وحدد المطلوب، واستعمل المعلومات المعطاة لحلها. لدى فيصل بركة سباحة سطحها على شكل مستطيل أبعاده ft 25، وأراد أن يرصف حولها ممرا متساوي العرض، إذا كانت مساحة سطح البركة مع الممر ft2 672، فما عرض الممر؟ 172 2.75 ft A 3 ft B الفصل 3 كثيرات الحدود ودوالها 3.25 ft C 3.5 ft D وزارة التعليم Ministry of Education 2024-1446

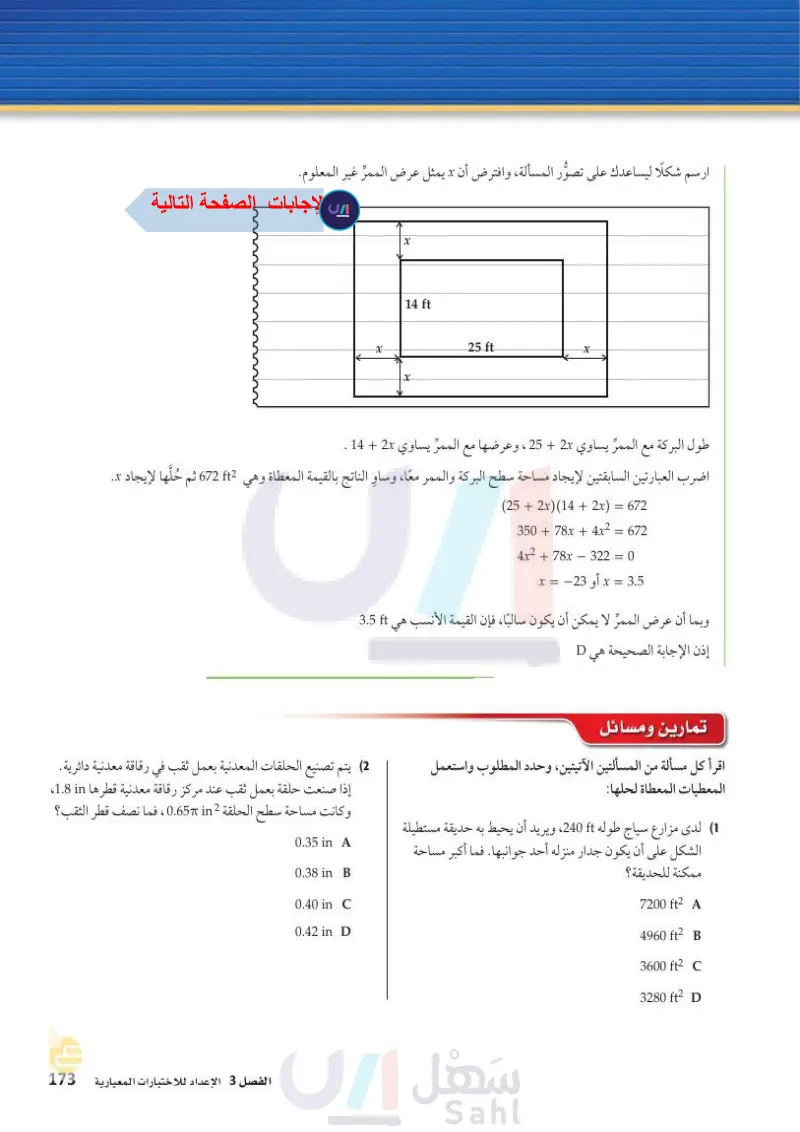
ارسم شكلا ليساعدك على تصوُّر المسألة، وافترض أن x يمثل عرض الممر غير المعلوم. x X 14 ft X 25 ft x طول البركة مع الممر يساوي 2 + 25 ، وعرضها مع الممر يساوي 2x +14. اضرب العبارتين السابقتين لإيجاد مساحة سطح البركة والممر معًا، وساءِ الناتج بالقيمة المعطاة . ft2 672 ثم حُلَّها لإيجاد x. وهي 3.5 ft (25+ 2x) (14+ 2x) = 672 35078x+4x² = 672 4x²+78x322 = 0 3.5 = x أو 23− = x وبما أن عرض الممر لا يمكن أن يكون سالبًا، فإن القيمة الأنـ إذن الإجابة الصحيحة هي D تمارين ومسائل اقرأ كل مسألة من المسألتين الآتيتين، وحدد المطلوب واستعمل المعطيات المعطاة لحلها (1) لدى مزارع سياج طوله 240 ويريد أن يحيط به حديقة مستطيلة الشكل على أن يكون جدار منزله أحد جوانبها. فما أكبر مساحة ممكنة للحديقة؟ (2 يتم تصنيع الحلقات المعدنية بعمل ثقب في رقاقة معدنية دائرية. إذا صنعت حلقة بعمل ثقب عند مركز رقاقة معدنية قطرها in 1.8 وكانت مساحة سطح الحلقة 2 in 0.65 ، فما نصف قطر الثقب؟ 0.35 in A 0.38 in B وزارة التعليم Ministry of Education الفصل 3 الإعداد للاختبارات المعيارية 217314 0.40 in C 0.42 in D 7200 ft² A 4960 ft² B 3600 ft² C 3280 ft² D

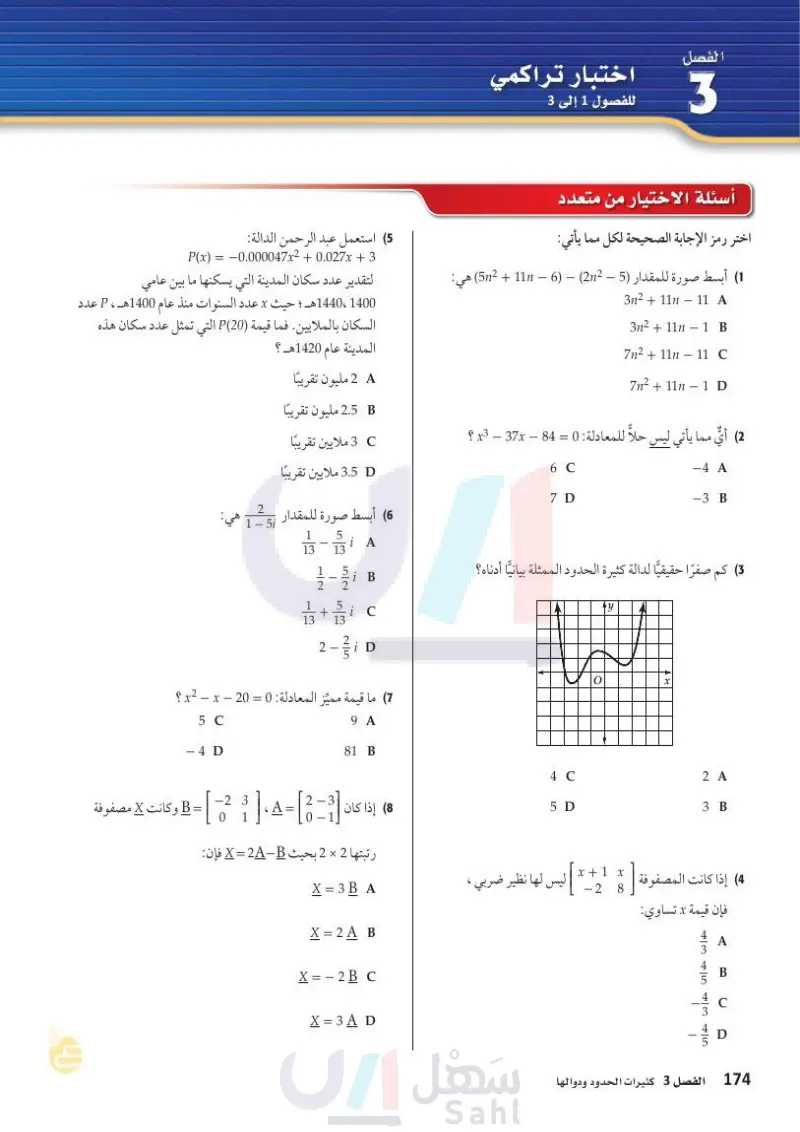
الدالة: (5) استعمل عبد الرحمن P(x) = -0.000047x2 + 0.027x + 3 الفصل 3 اختبار تراكمي أسئلة الاختيار من متعدد اختر رمز الإجابة الصحيحة لكل مما يأتي: (1) أبسط صورة للمقدار (5) - (212) – (6 - 5n2 + 11n) 3n2 + 11n - 11 A 3n2 + 11n - 1 B 7n2+11n11 C 7n2 + 11n - 1D هي: (2) أي مما يأتي ليس حلاً للمعادلة: 0 = 84 - x3 – 37x ؟ -4 A 3 B 6 7 D لتقدير عدد سكان المدينة التي يسكنها ما بين عامي 1400 ،1440هـ ؛ حيث x عدد السنوات منذ عام 1400هـ ، P عدد السكان بالملايين. فما قيمة (20)P) التي تمثل عدد سكان هذه المدينة عام 1420هـ ؟ 2A مليون تقريبا B 2.5 مليون تقريبًا 3 ملايين تقريبًا 3.5D ملايين تقريباً (6) أبسط صورة للمقدار 2 1 - 5i هي: 1 13 - 5 13 i A 12 5 - 102 i B 1 5 + i C 13 13 2- Bi D (7 ما قيمة مميّز المعادلة : 0 = 20 - x2 - x ؟ 5 - 4 D 9 A 81 B 8) = B وكانت X مصفوفة إذا كان [3-2] =A، [ 1 2 ]- -2 3 0 رتبتها 2 × 2 بحيث X = 2A-B فإن : وزارة التعليم Ministry of Education 2024-1446 X = 3 B A X = 2A B X=-2B C X = 3AD (3 كم صفرًا حقيقيًّا لدالة كثيرة الحدود الممثلة بيانيا أدناه؟ y X 4 C 5 D 2A 3 B ] ليس لها نظير ضربي ، ، x + 1 x -2 8 مصفوفة [ (4) إذا كانت المصفوفة فإن قيمة x تساوي: 43 45 43 45 حراس الفصل 3 كثيرات الحدود ودوالها A B D 174

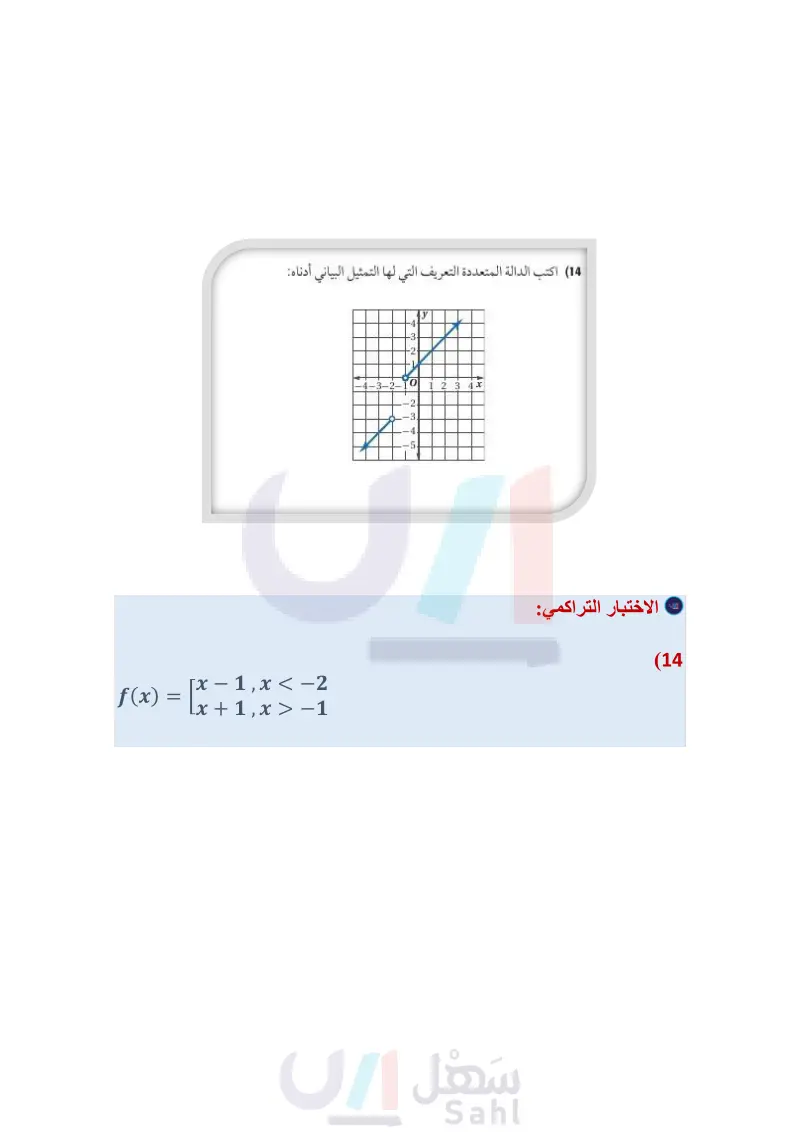
أسئلة ذات إجابات قصيرة (9) يبين الشكل الآتي حديقة محاطة بممر عرضه x مترًا. فإذا علمت 13) يريد صالح أن يملأ الإناء المكعب بالماء مستعملا العلبة أن مساحة الحديقة مع الممر m2 558 ، فأوجد عرض الممر الأسطوانية في الشكل أدناه. فكم مرة يستعمل العلبة؟ -2 in. 6 in. 15 in X 25 m X 12 m بالأمتار. (10) حلّل المقدار : ab3 + 64 تحليلا تاما، وبين خطوات الحل. 11) بسط المقدار : 3x3 – 4x2 - 28x 16 x + 2 واكتب إجابتك على صورة حاصل ضرب عوامل مبينا خطوات أسئلة ذات إجابات مطولة (14) اكتب الدالة المتعددة التعريف التي لها التمثيل البياني أدناه: 432- -4-3-2-10 -2 -3. -4 -5. У 1 2 3 4 x الحل. (12) ما قيمة a في المعادلة المصفوفية الآتية؟ 23-8-4 a = [29] هل تحتاج إلى مساعدة إضافية ؟ 14 13 12 •11 10 9 8 7 6 5 4 3 2 1 1-3 3-812-5 3-4 3-5 3-6 2 2-2 3-2 3-1 3-5 2-5 3-8 8 3-6 3-3 Ministry of Education الفصل 3 اختبار تراكمي 2175144 إذا لم تستطع حل سؤال .. فعد إلى الدرس .