القانون العام والمميز - رياضيات2-1 - ثاني ثانوي

رابط الدرس الرقمي www.ien.edu.sa القانون العام والمميز The Quadratic Formula and the Discriminant 3-2 فيما سبق: درست حل معادلات تربيعية بإكمال المربع. (مهارة سابقة) والان أحل معادلات تربيعية باستعمال القانون العام. أستعمل المميز لأحدد عدد جذور معادلة تربيعية وأنواعها المفردات القانون العام Quadratic Formula المميز discriminant لماذا ؟ سهم نحو هدف على الأرض، ويمكن أُطلق التعبير عن ارتفاعه عن الأرض بالدالة التربيعية: h = -4.92 + 117t + 42 حيث ارتفاع السهم بعد t ثانية من إطلاقه، وللتنبؤ بالزمن اللازم لوصول السهم إلى الهدف، نحل المعادلة .-4.92 +117 +42 = 0 ومن الصعب حل هذه المعادلة باستعمال التحليل إلى العوامل، أو التمثيل البياني، أو إكمال المربع. القانون العام : تمكنت سابقا من حل بعض المعادلات التربيعية بالتمثيل البياني، أو بالتحليل إلى العوامل، أو باستعمال خاصية الجذر التربيعي، أو بإكمال المربع ، أو باستعمال القانون العام؛ وهو قانون يمكن استعماله لحل أية معادلة تربيعية، ويمكن اشتقاق هذا القانون من خلال حل معادلة تربيعية على الصورة القياسية. مثال 2x2 + 8x + 1 = 0 X2 + 4x + 1 = 0 x2 x2 x² + 4x = -1 1/1 2 x² + 4 x + ( ±² )² = − − 1 + ( ²±²)² x2 (x + 2)² = − +(²)² (x + 2)² = 77 2 x+2= x + 2 = +1 7 x = - -2± -4 + V14 معادلة تربيعية على الصورة القياسية اقسم كلا الطرفين على a اطرح من كلا الطرفين أكمل المربع حلل الطرف الأيسر بسط الطرف الأيمن خاصية الجذر التربيعي من كلا الطرفين بسط b 2a اطرح الحالة العامة ax2 + bx + c = 0 x2 + b x + 4 = 0 a a b x2 + x = a b b2 x2 + -x+ a =- + a b2 2a b ( x + 21 )² = − 5 + b² 2a a b 2a (x + 2)² = b² - 4ac b2 4a2 b Vb2 - 4ac x + = 2a 20 وزارة التعليم = x بالقانون العام لحل المعادلات التربيعية. Ministry of Education الدرس - القانون العام والمميز 211514 b x = - + 20 b2 - 4ac 2a x = -b + Vb2 - 4ac 20 -b +Vb2 – 4ac 2a تعرف المعادلة:

إرشادات للدراسة القانون العام على الرغم من أن طريقة التحليل إلى العوامل قد تكون الأسهل لحل بعض المعادلات التربيعية، إلا أن القانون العام يحل أي معادلة تربيعية. مفهوم أساسي التعبير اللفظي مثال : أضف إلى القانون العام لحل المعادلة التربيعية مطويتك يمكن حل المعادلة التربيعية المكتوبة على الصورة: 0 ax2 + bx + c = a باستعمال القانون -b + Vb2 4ac x= 2a x2 + 5x + 6 = 0 → x = -5±√52-4(1)(6) 2(1) مثال 1 معادلة لها جذران نسبيان حل المعادلة : 11 = 10 - x2 باستعمال القانون العام. أولًا اكتب المعادلة على الصورة 0 = ax 2 + x + c ، وحدد قيم كل من abc . ax2 + bx + C = 0 ↓ ↓ ↓ x2 - 10x = 11 1x2 – 10x - 11 = 0 القانون العام عوض عن a بالعدد 1 6 بالعدد 10- ، C بالعدد 11- ثم عوض بعد ذلك بتلك القيم في القانون العام. -b + Vb2 ― 4ac x = 2a -(-10)±√(-10)² - 4(1)(-11) 2(1) اضرب 10 ± √√100 +44 2 بسط 10 ± 144 2 √144 = 12 = 10 ± 12 2 اكتب X على صورة معادلتين 10 - 12 10 +12 X = X = 2 2 بسط = −1 = 11 وعليه يكون الحلان هما: 11، 1-. تحقق عوض كلتا القيمتين في المعادلة الأصلية. x2 - 10x = 11 x²-10x: (11)² - 10(11) 11 x2 - 10x = 11 (−1)² – 10(−1) = 11 12111011 ✓ 11 = 11 2x2 + 25x + 33 = 0 (1B 1+1011 ✓ 11 = 11 تحقق من فهمك x2 + 6x = 16 (1) عندما يكون ما تحت الجذر في القانون العام صفرًا، فإننا نحصل على جذرٍ نسبي واحد، ويكون حل المعادلة في هذا الجذر النسبي، ولكنه مكرر مرتين . هذه الحالة هو وزارة التعليم Ministry of Education 2024-1446 الفصل 3 كثيرات الحدود ودوالها 116

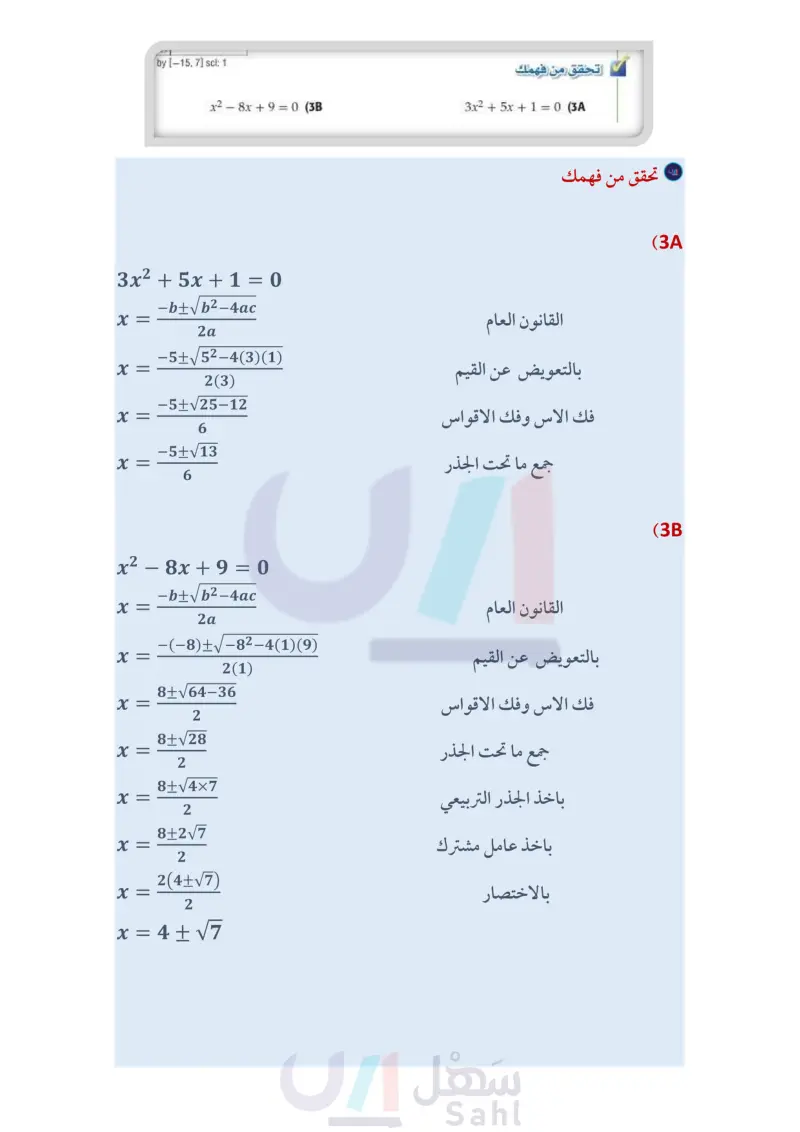
مثال 2 معادلة لها جذر نسبي واحد (مكرر مرتين) حل المعادلة : 0 = 16 + x2 + x باستعمال القانون العام . حدد قيم كل من a،bc ، وعوّض هذه القيم في القانون العام . القانون العام عوض عن a بالعدد 1 وعن b بالعدد 8 ، وعن C بالعدد 16 -117 6/67 y f1(x)=x²+8.x+16 1. 10 (-4,0) -6.67 1.1 10 [-10, 10] scl: 1 by [-6.67, 6.67] scl: 1 10 - b + Vb2 X = 20 4ac -(8) ± √ (8)² - 4(1)(16) 2(1) بسط -8 ± 0 √0=0 = = = -4 الحل هو 4 - مكرر مرتين) . تاريخ الرياضيات براهام جوبتا (598-668 م ) عالم رياضيات هندي، وهو أول من أوجد حلا عاما للمعادلة التربيعية في الصورة ax² + bx = c وهو ما يُسمَّى الآن القانون العام لحل المعادلة التربيعية. تحقق : تحقق من صحة الحل بتمثيل الدالة المرتبطة بالمعادلة 16 + y = x2 + 8x بيانيًّا. مستعملا خاصية الصفر في الحاسبة البيانية للحصول على قيمة صفر الدالة المرتبطة وهو : 4- = x تحقق من فهمك x2 + 34x + 289 = 0 (2 x2 - 16x + 64 = 0 (2 يمكنك التعبير عن الجذور غير النسبية بكتابتها في الصورة الجذرية . الجذور غير النسبية مثال 3 إرشادات للدراسة إظهار كامل التمثيل البياني: لإظهار التمثيل البياني للدالة كاملا على الشاشة. اضغط مفتاح menu ومنها اختر 4 تكبير / تصغير النافذة ثم اختر ::1: إعدادات النافذة لتحدد التدريج المناسب للمتغير y فاختر مثلا حُلَّ المعادلة : 0 = 7 - 6x + 2 2 باستعمال القانون العام. - b + Vb2 - 4ac X = 20 = -(6) ± √(6)² - 4(2)(-7) 2(2) -6 ±√√√92 4 القانون العام بسط عوض عن a بالعدد ،2 وعن b بالعدد 6 ، وعن C بالعدد 7 115b 77y 1.2 1.1 f1(x)=2x²+6x-7 -15 [−10, 10] scl: 1 by [-15, 7] scl: 1 وزارة التعليم Ministry of Education 10 -6±2√23-3±√23 2 √92 = =1 4 (23) = 2√23 = 4 الحلان التقريبيان هما: 0.9 ، 3.9 تحقق: تحقق من صحة الحل بتمثيل الدالة المرتبطة بالمعادلة 7 - y = 2x2 + 6x بيانيًا. مستعملاً خاصية الصفر في الحاسبة البيانية للحصول على القيمتين التقريبيتين لصفري الدالة المرتبطة وهما: -3.9, 0.9 تحقق من فهمك x2 – 8x + 9 = 0 (3B 3x2 + 5x + 1 = 0 (3 الدرس - القانون العام والمميز 211714 -15 القيمة الصغرى : القيمة العظمى ل - ۷:

إرشادات للدراسة الأعداد المركبة تذكر أن تكتب حلك في الصورة a + bi ، وهذه الصورة تُسمّى الصورة القياسية للعدد المركب. إذا كان ما تحت الجذر في القانون العام عددًا ،سالبًا، فإن الحلين يكونان عددين مركبين مترافقين. مثال 4 الجذور المركبة حُلَّ المعادلة: 10- = x2 – 6x باستعمال القانون العام. - -b + Vb2 - 4ac x = القانون العام 2a عوض عن a بالعدد 1 ، وعن 6 بالعدد 6 - ، وعن C بالعدد 10 بسط -(-6) ±√(-6)² 2(1) 2 - 4(1)(10) 6 ± V-4 2 √-4 = = √√4. - -1) = 2i 6 ± 2i 2 بسط = 3 + i 0.5 -116 1.1 f1(x)=x²-6 -6.x+10 -5 [-5, 11] scl: 0.5 by [-5, 8] scl: 1 الحلان :هما i . 3 + i - 3 وهما عددان مركبان مترافقان : تحقق يظهر التمثيل البياني للدالة المرتبطة بالمعادلة أن الحلّين عددان مركبان، ولكن لا يساعدك التمثيل البياني على إيجادهما وللتحقق من صحة الحلين المركبين عوّضهما في المعادلة الأصلية. المعادلة الأصلية x = 3 + i أوجد مفكوك (2) + (3) وخاصية التوزيع بسط i2 = -1 المعادلة الأصلية x = 3 - i أوجد مفكوك 2 - 3 وخاصية التوزيع بسط. 12 = -1 x2 – 4x = -13 (4B x2 - 6x = -10 x²-6x (3 + 1)² - 6(3 + i) = -10 9 + 6i + i2 – 18 – 6i ÷ -10 -912-10 ✓-9-1=-10 x2 - 6x = -10 (3-1)26(3-i) = -10 9 - 6i + 12 - 18 + 6i = -10 -912-10 ✓-9-1=-10 تحقق من فهمك 3x2 + 5x + 4 = 0 (4 الجذور والمميز في المعادلة التربيعية، لاحظ العلاقة بين قيمة ما تحت الجذر وجذور المعادلة التربيعية في الأمثلة السابقة. العبارة b2 – 4ac تسمى المميز. -b + Vb2 - 4ac x = 2a ← المميز ويمكنك استعمال المميز لتحديد عدد جذور المعادلة التربيعية وأنواعها ، والجدول في الصفحة الآتية يلخص الأنواع الممكنة للجذور ، وذلك للتأكد من صحة حلك. وزارة التعليم Ministry of Education 2024-1446 الفصل 3 كثيرات الحدود ودوالها 118

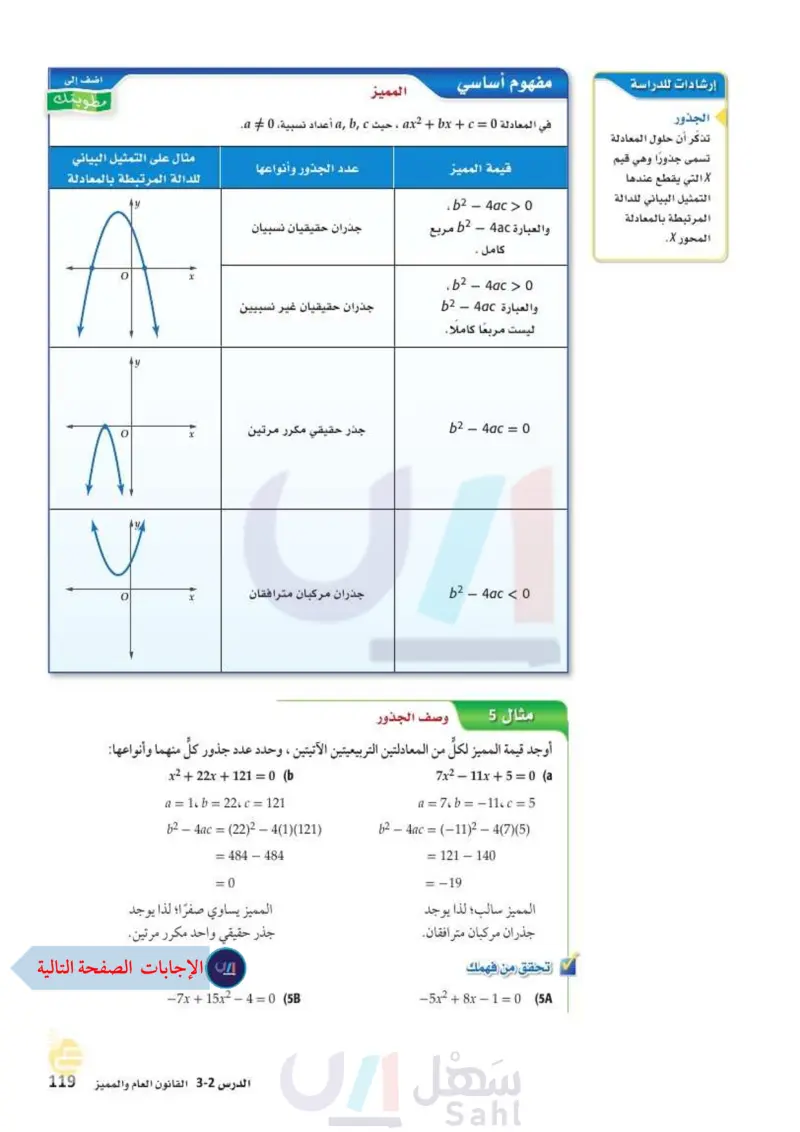
إرشادات للدراسة الجذور تذكر أن حلول المعادلة تسمى جذورًا وهي قيم X التي يقطع عندها التمثيل البياني للدالة المرتبطة بالمعادلة المحور X. مفهوم أساسي المميز في المعادلة 0 = ax 2 + x + c ، حيث أعداد نسبية 0 / a. قيمة المميز ، b2 ― 4ac > 0 والعبارة 4ac - 62 مربع ' اضف إلى مطويتك عدد الجذور وأنواعها مثال على التمثيل البياني للدالة المرتبطة بالمعادلة جذران حقيقيان نسبيان X AM x x جدران حقيقيان غير نسبيين جذر حقيقي مكرر مرتين جدران مركبان مترافقان . كامل . 4ac > 0 .b2 b2 - والعبارة 4ac - 62 ليست مربعًا كاملا b2-4ac = 0 b2-4ac0 مثال 5 وصف الجذور أوجد قيمة المميز لكلِّ من المعادلتين التربيعيتين الآتيتين ، وحدد عدد جذور كلّ منهما وأنواعها: x2 + 22x + 121 = 0 (b a = 1. b = 22، c = 121 b2 - 4ac = (22)2 - 4(1)(121) = 484-484 = 0 7x2 – 11x + 5 = 0 (a a = 7، b = -11، c = 5 b2 – 4ac = (11)2 - 4(7)(5) = 121 - 140 = −19 المميز سالب؛ لذا يوجد جذران مركبان مترافقان. تحقق من فهمك المميز يساوي صفرًا؛ لذا يوجد جذر حقيقي واحد مكرر مرتين. وزارة التعليم Ministry of Education -7x+15x²-4=0 (5B الدرس 32 القانون العام والمميز 211914 -5x28x-1=0 (5A

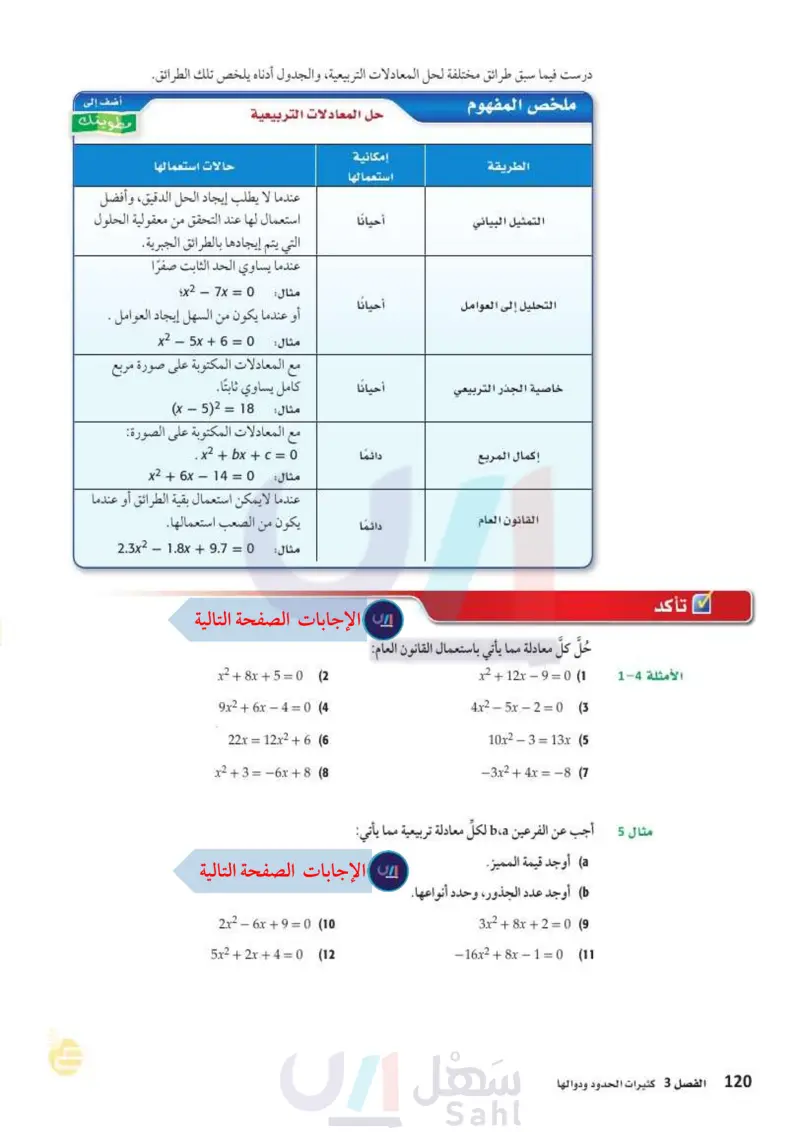
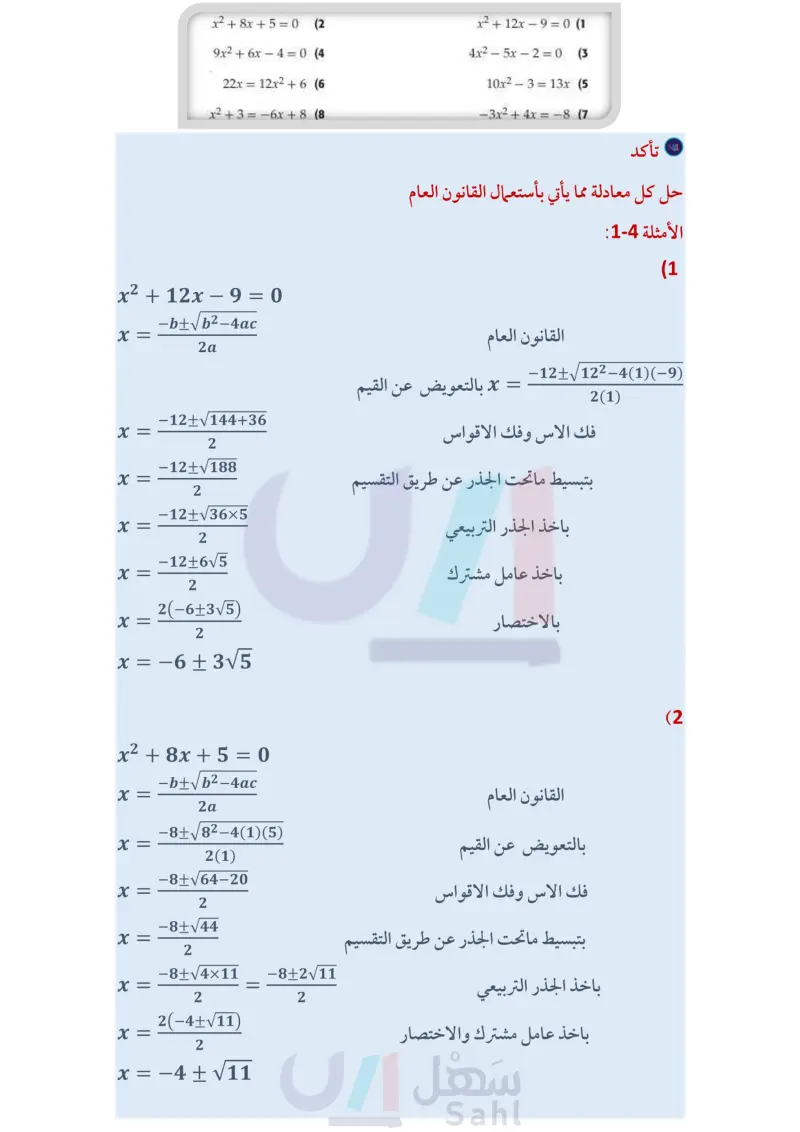
120 تأكد درست فيما سبق طرائق مختلفة لحل المعادلات التربيعية، والجدول أدناه يلخص تلك الطرائق. ملخص المفهوم حل المعادلات التربيعية أضف إلى مطويتك الطريقة إمكانية استعمالها حالات استعمالها عندما لا يطلب إيجاد الحل الدقيق، وأفضل التمثيل البياني أحيانًا استعمال لها عند التحقق من معقولية الحلول التي يتم إيجادها بالطرائق الجبرية. عندما يساوي الحد الثابت صفرًا مثال: x2 - 7x = 0 التحليل إلى العوامل أحيانًا أو عندما يكون من السهل إيجاد العوامل . مثال: x2 – 5x + 6 = 0 مع المعادلات المكتوبة على صورة مربع خاصية الجذر التربيعي أحيانًا كامل يساوي ثابتًا. إكمال المربع دائما (x – 5)2 = 18 مثال: مع المعادلات المكتوبة على الصورة: . x 2 + x + C = 0 x2 + 6x – 14 = 0 مثال: عندما لا يمكن استعمال بقية الطرائق أو عندما القانون العام دائما يكون من الصعب استعمالها . مثال: 2.3x2 - 1.8x + 9.7 = 0 الأمثلة 1,4 حُلَّ كلّ معادلة مما يأتي باستعمال القانون العام: x2 + 12x - 9 = 0 (1 4x2 – 5x - 2 = 0 (3 10x2 – 3 = 13x (5 -3x2 + 4x = -8 (1 مثال 5 أجب عن الفرعين ba لكل معادلة تربيعية مما a أوجد قيمة المميز. ( أوجد عدد الجذور، وحدد أنواعها. يأتي: 3x2 + x + 2 = 0 (9 -16x2 + 8x - 1 = 0 (11 الفصل 3 كثيرات الحدود ودوالها x2 + 8x + 5 = 0 (2 9x2 + 6x - 4 = 0 (4 22x = 12x2 + 6 6 x2 + 3 = 6x + 8 8 2x2 - 6x + 9 = 0 (10 5x2 + 2x + 4 = 0 (12 وزارة التعليم Ministry of Education 2024-1446

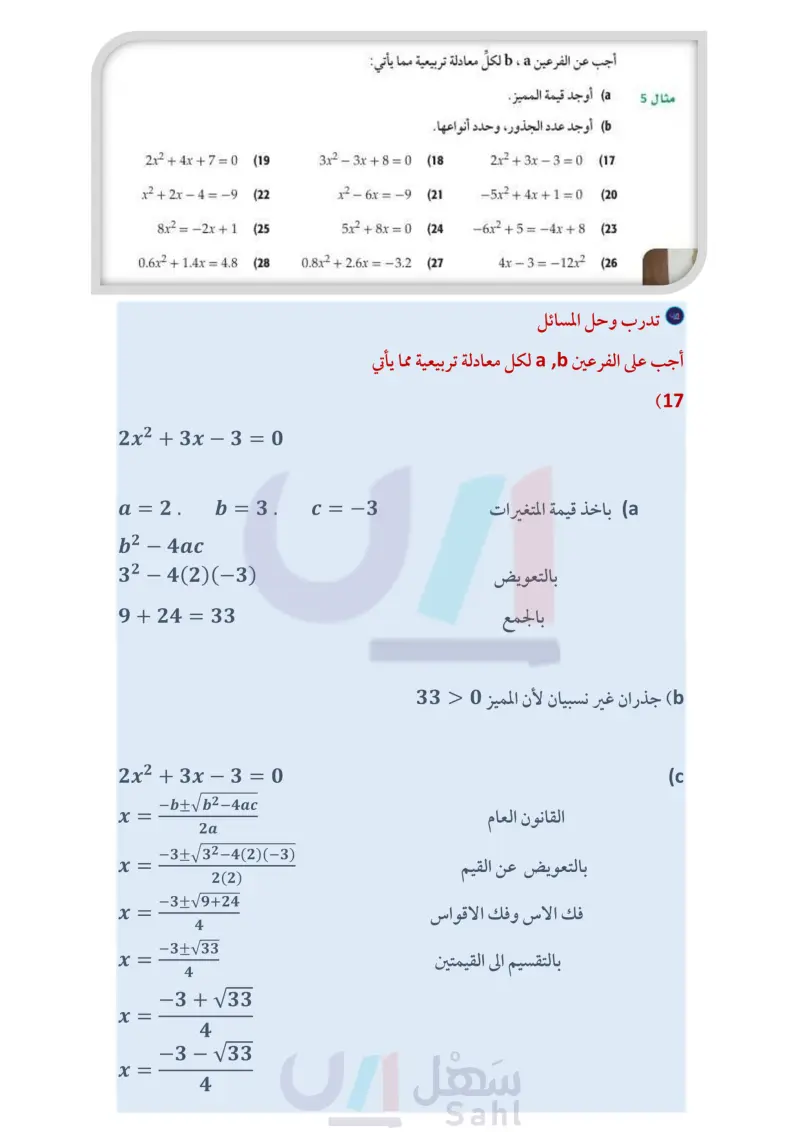
تدرب وحل المسائل حُلَّ كلّ معادلة مما يأتي باستعمال القانون العام: الأمثلة 1,4 x2 + 45x = -200 (13 5x2 - 9 = 11x (15) أجب عن الفرعين b ، a لكل معادلة تربيعية مما يأتي: مثال 5 a أوجد قيمة المميز. أوجد عدد الجذور، وحدد أنواعها. 4x2 - 6 = -12x (14 12x29x-2=-17 (16 2x2 + 4x + 7 = 0 (19 3x2 – 3x + 8 = 0 (18 2x2 + 3x - 3 = 0 (17 x2 + 2x - 4 = -9 (22 x2 - 6x = -9 (21 -5x2 + 4x + 1 = 0 (20 8x2 = −2x + 1 (25 5x2 + 8x = 0 (24) -6x2 + 5 = -4x + 8 (23 0.6x2 +1.4x4.8 (28 0.8x2 + 2.6x = -3.2 (27 4x - 3 = -12x2 (26 الربط مع الحياة تأسس برنامج مكافحة التدخين التابع لوزارة الصحة في المملكة العربية السعودية في 1423/2/23هـ؛ لمكافحة التدخين بكافة أنواعه ووسائله. ويقدم خدماته (29) التدخين: تبذل دول العالم جهودًا مكثفة للتوعية بأخطار التدخين، وقد أثمرت عن تناقص أعداد المدخنين. وفي إحدى البلدان أجريت دراسة حول الإصابات بمرض سرطان الرئة بين كل 100000 شخص في بعض الأعوام، وكانت نتائجها التقريبية كما في الجدول المجاور. ويمكن تمثيل العدد التقريبي للمصابين بالدالة 91.81 + y = −0.26x2 - 0.55x، حيث x عدد السنوات بعد عام 2000. احسب عدد المصابين بسرطان الرئة لكل 100000 شخص في عامي . 2017,2010 عدد الإصابات العام لكل 100000 92 2000 90 2002 85 2004 ? 2010 ? 2017 استعمل القانون العام لإيجاد قيمة x عندما 50 = y. اعتمادًا على الدالة التربيعية، متى يصبح معدل الإصابة يساوي صفرًا؟ وهل هذا التوقع معقول؟ فسّر إجابتك. في كافة المجالات التوعوية (30) نظرية الأعداد يعطى مجموع الأعداد الصحيحة المتتالية « ، ... ،3 ،2 ،1 بالقانون والعلمية والاستشارية المتعلقة بالتدخين وأضراره وطرق مكافحته في مدن ومحافظات المملكة. المصدر : البوابة الإلكترونية لوزارة الصحة www.moh.gov.sa/depts/TCP/Pages/ About.aspx (1) + S = = n (n. فكم عددًا صحيحًا متتاليا بدءًا بالعدد 1 مجموعها يساوي 666؟ (31) ترفيه : يُعطى ارتفاع لعبة ترفيهية عن سطح الأرض وهي تتحرك بسرعة تصل إلى ft\s 80 بالدالة: 60 + h = 16t2 - 64t ؛ حيث الارتفاع بالأقدام، و الزمن بالثواني. فإذا علمت أنها ترتفع مسافة ، فما الزمن الذي يستغرقه هبوطها من ارتفاع ft 60 إلى Oft ؟ 6 وزارة التعليم Ministry of Education الدرس - القانون العام والمميز 212114

مسائل مهارات التفكير العليا (32) اكتشف الخطأ : دت كل من هدى وندى عدد حلول للمعادلة 7 = 3x2 – 5x. فمن منهما إجابتها حددت صحيحة؟ وضّح إجابتك. هدى ندى 3x²-5x=7 b² - 4ac = (-5)² - 4(3)(7) =-59 3x²-5x=7 3x2 - 5x - 7 = 0 62-4ac = (-5)² - 4(3)(-7) = 109 وبما أن المميز موجب فللمعادلة حلان وبما أن المميز سالب فلا توجد للمعادلة حلول حقيقية. حقيقيان تدريب على اختبار (33) تحد: حل المعادلة 0 = 4ix 2 - 4ix + 5i باستعمال القانون العام. 34) تبرير: حدد ما إذا كانت كل جملة مما يأتي صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. ووضّح إجابتك: a إذا كانت إشارتا كل من المعاملين acc في المعادلة التربيعية المكتوبة على الصورة القياسية مختلفتين، فإن جذري المعادلة حقيقيان. إذا كان مميز المعادلة التربيعية أكبر من ،1 فإن لها جذرين حقيقيين غير نسبيين. (35) اكتب صف ثلاث طرائق مختلفة لحل المعادلة : 20 = 15 - x2 - 2x . وأيها تفضل؟ ولماذا؟ (36) أي المعادلات الآتية لها جذر حقيقي مكرر مرتين؟ (37) قيمة المميز للمعادلة 0 = x2 – 8x هي: وزارة التعليم Ministry of Education 2024-1446 -64 A -8 B 8 C 64 D x2 - 2x + 5 = 0 x2 - 2x - 5 = 0 B x2 = 19 C x2 - 8x = -16 D - مراجعة تراكمية أوجد قيمة C التي تجعل كل ثلاثية حدود مما يأتي مربعًا كاملا. ثم اكتبها على صورة مربع كامل: (مهارة سابقة) x² + 1/1x +c (40 (4√-9). (2√-25) (43 x2 + 2.4x + C (39) 7-16 (42) x2 + 13x + c 38 بسط كلا مما يأتي: الدرس (1-3) الفصل 3 كثيرات الحدود ودوالها i26 (41 122