المجسمات - الرياضيات العلمي - سادس اعدادي
الفصل الأول: الأعداد المركبة
الفصل الثاني: القطوع المخروطية
الفصل الثالث: تطبيقات التفاضل
الفصل الرابع: التكامل
الفصل الخامس: المعادلات التفاضلية الاعتيادية
الفصل السادس: الهندسة الفضائية
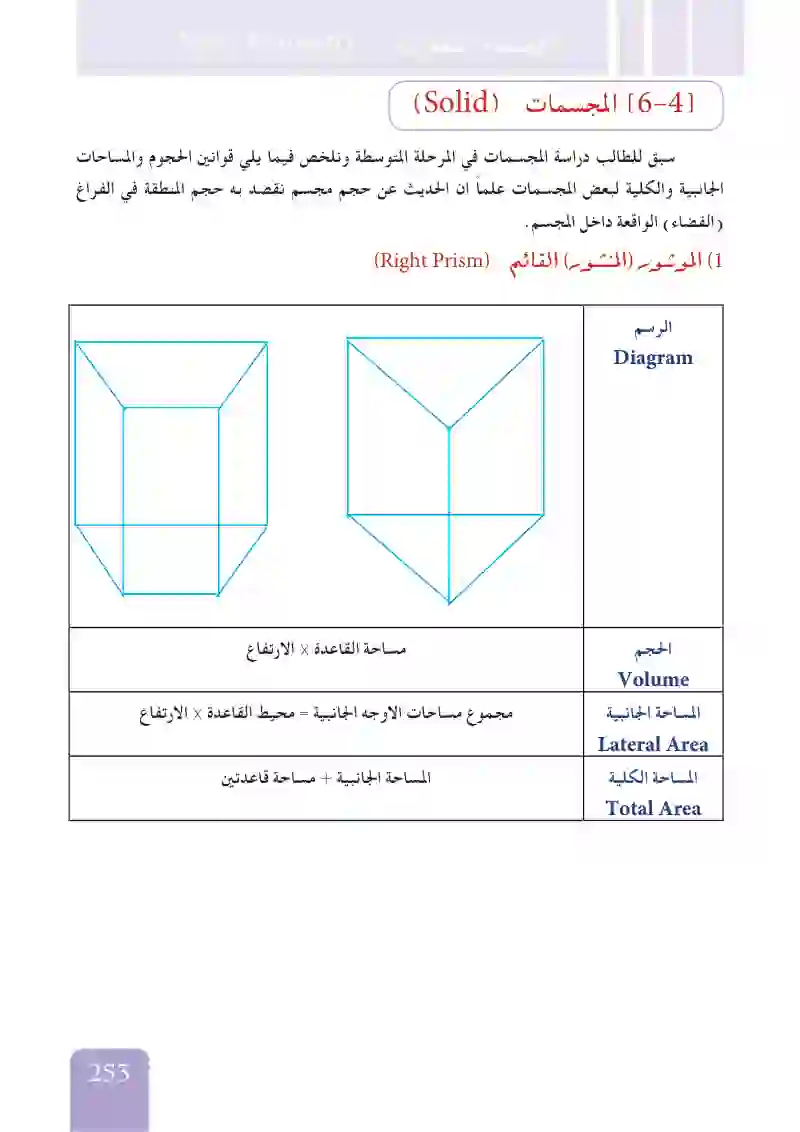
المجسمات الموشور القائم
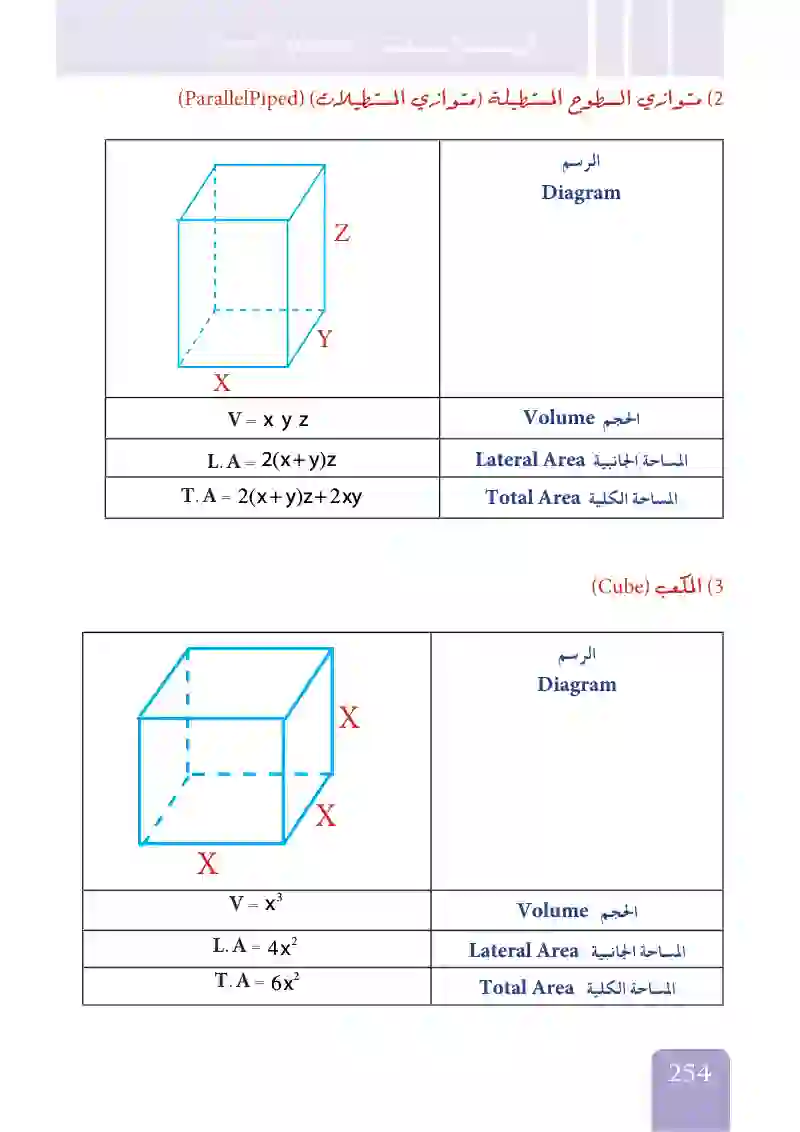
متوازي السطوع المستطيلة (متوازي المستطيلات)
المكعب
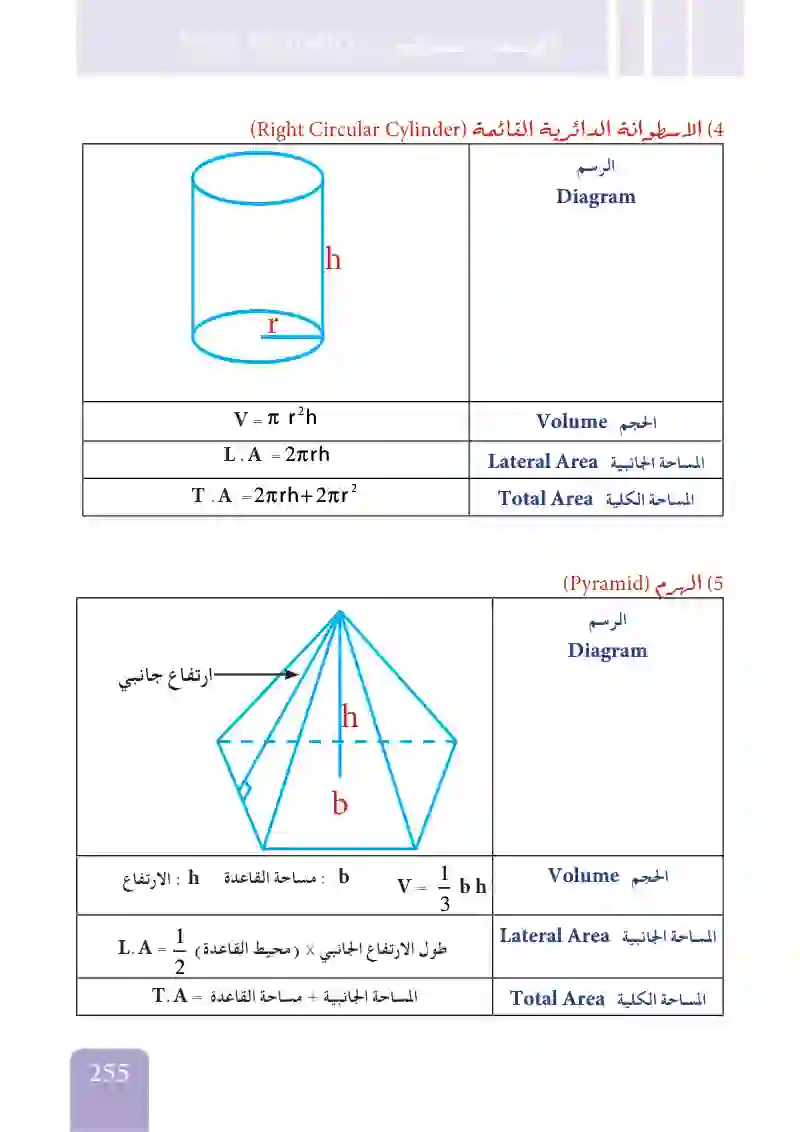
الأسطوانة الدائرية القائمة
الهرم
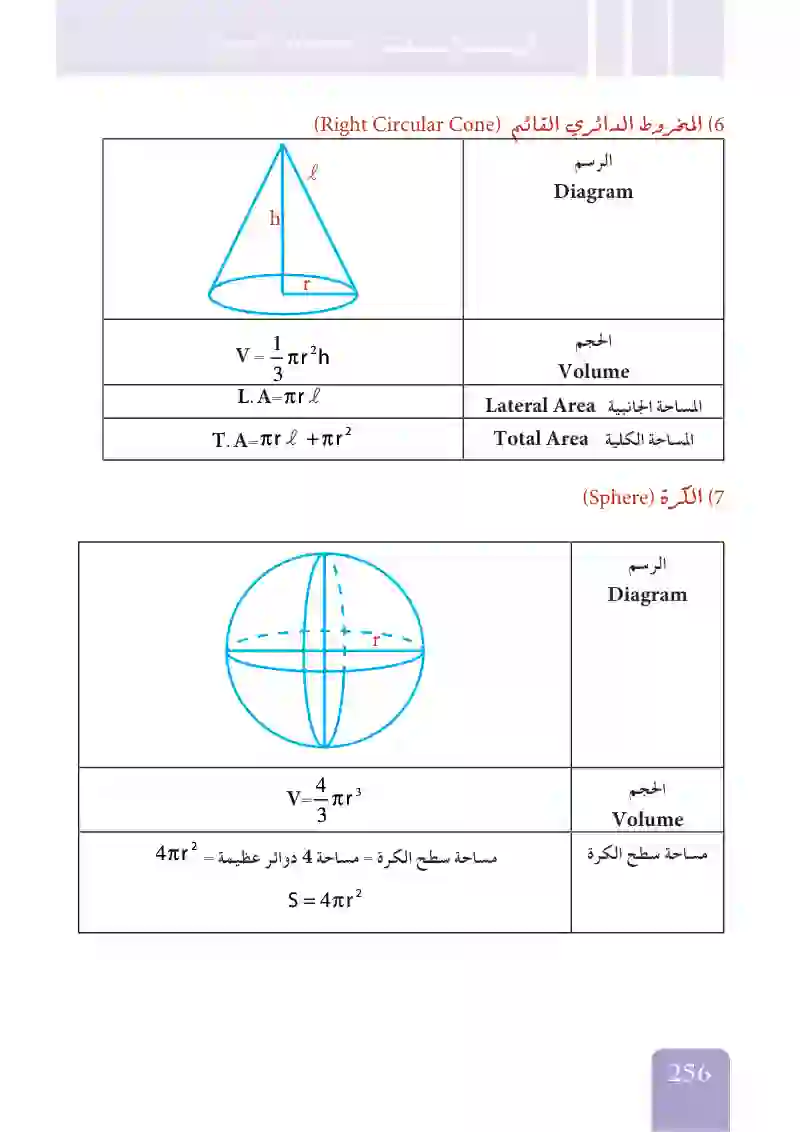
المخروط الدائري القائم
الكرة
\ذو الوجوه الأربعة المنتظم

إذا كانت المساحة الكلية لمتوازي المستطيلات = 2^724cm ومساحة قاعدته = 2^132cm ومساحة أحد أوجهه الجانبية = 2^110cm جد حجمه
أسطوانة دائرية قائمة مساحتها الجانبية 400∏cm^2 وحجمها 2000cm^3 أوجد ارتفاعها ونصف قطر قاعدتها
مخروط دائري قائم مر برأسه مستو فقطع قاعدته بقطعة مستقيم تبعد عن مركز القاعدة بمقدار 8cm فاذا كانت مساحة المقطع = 2^102cm وارتفاع المخروط = 15cm احسب : حجمه
إذا علمت أنه يمكن رسم كرة خارج ذي الوجوه الأربعة المنتظم برهن أن نصف قطر الكرة = 3/4 الارتفاع
برهن على أن حجم ذي الوجوه الأربعة المنتظم والذي طول حرفه = L هو √2ℓ^3/12 وحدة مكعبة

جد قيمة x,y∈R والتي تحقق y/1+i=x^2+4/x+2i
إذا كان z=1-√3i/1+√-3 عدد مركبا جد باستخدام مبرهنة ديموافر z^1/2
قطع ناقص مركزه نقطة الأصل وقطع زائد نقطة تقاطع محوريه نقطة الأصل. كل منهما يمر ببؤرة الآخر فإذا كانت 9x^2+25y^2=225 معادلة القطع الناقص فجد محيط القطع الناقص
جد معادلة القطع الناقص الذي بؤرتاه تنتميان تحور السينات ومركزه نقطة الأصل ومساحة منطقته 7∏ وحدة مربعة ومحيطه يساوي 10∏ وحدة
جد dy/dx لكل مما يأتي x^3y^2-2y=5x+3
جد ناتج (3ω^9n+5/ω^5+4/ω^4)^6 ,n∈z

استخدم مبرهنة رول ثم مبرهنة القيمة المتوسطة لإيجاد قيم C للدالة x∈[-2,2], f(x)=x^4-2x^2
متوازي سطوح مستطيلة قاعدته مربعة وارتفاعه ثلاثة أمثال طول قاعدته ، جد الحجم التقريبي له عندما يكون طول قاعدته 2.97cm
إذا كانت f(x)=5√31x+1 جد باستخدام نتيجة مبرهنة القيمة المتوسطة القيمة التقريبية إلى f(1.01)
جد تكاملات كلاً مما يأتي ∫(cos^4 x-sin^4 x)dx
حل المعادلة التفاضلية الآتية y`=cos^2 y/x,y=∏/4,x=1
حل المعادلة التفاضلية الآتية (x^2+3y^2)dx-2xy dy=0
حل المعادلة التفاضلية xy`=y-x حيث أن x=1,y=1
حل المعادلة التفاضلية dy/dx=-2xtan y حيث أن x=0 عندما y=∏/2
باستخدام معلوماتك في التفاضل أرسم المنحني البياني للدالة yx^2=1
مخروط دائري قائم حجمه 210∏cm^3 جد القيمة التقريبة لنصف قطر قاعدته إذا كان ارتفاعه 10cm
f(x)=ax^2-4x+5 دالة تحقق شروط مبرهنة رول على الفترة [-1,b] فإذا كانت c=2 تنتمي للفترة (-1,b) فجد قيمة a,b∈R





