تقعر وتحدب المنحنيات ونقط الانقلاب - الرياضيات العلمي - سادس اعدادي
الفصل الأول: الأعداد المركبة
الفصل الثاني: القطوع المخروطية
الفصل الثالث: تطبيقات التفاضل
الفصل الرابع: التكامل
الفصل الخامس: المعادلات التفاضلية الاعتيادية
الفصل السادس: الهندسة الفضائية

تقعر وتحدب المنحنيات ونقط الإنقلاب
المنحني مقعر في (a,b)
مبرهنة تقعر وتحدب دالتين
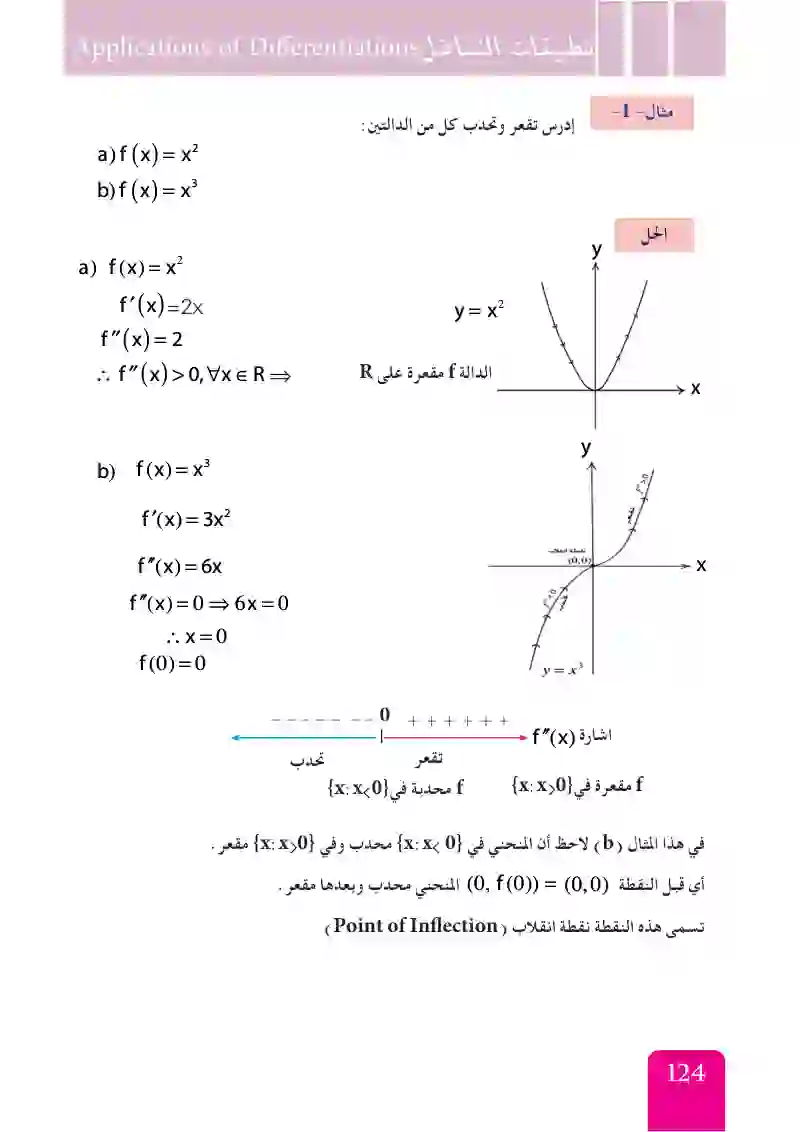
أدرس تقعر وتحدب كل من الدالتين f(x)=x^2
أدرس تقعر وتحدب كل من الدالتين f(x)=x^3

تدعى النقطة التي تنتمي لمنحني دالة والتي يتغير عندها منحني الدالة (من تقعر الى تحدب) أو بالعكس (من تحدب إلى تقعر) بنقطة إنقلاب لهذا المنحنى
جد نقطة الإنقلاب للمنحنى f(x)=2x^3-3x^2-12x+1
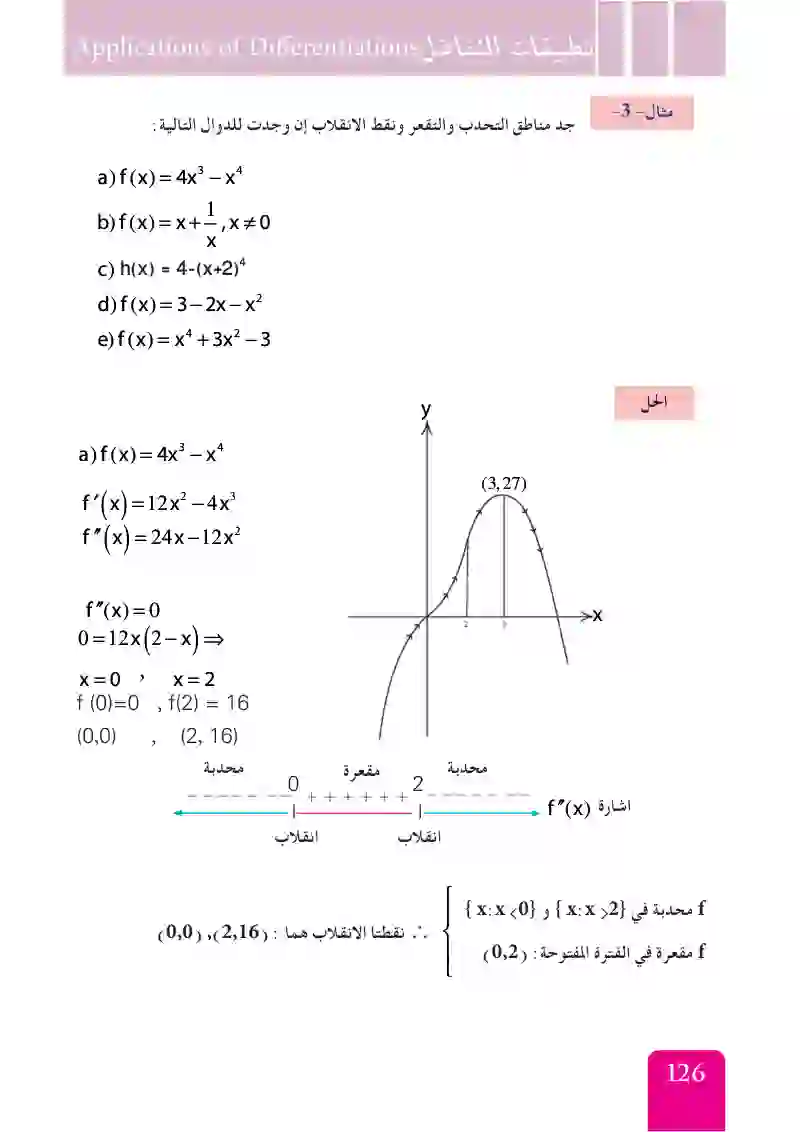
جد مناطق التحدب والتقعر ونقط الإنقلاب إن وجدت للدوال التالية f(x)=4x^3-x^4
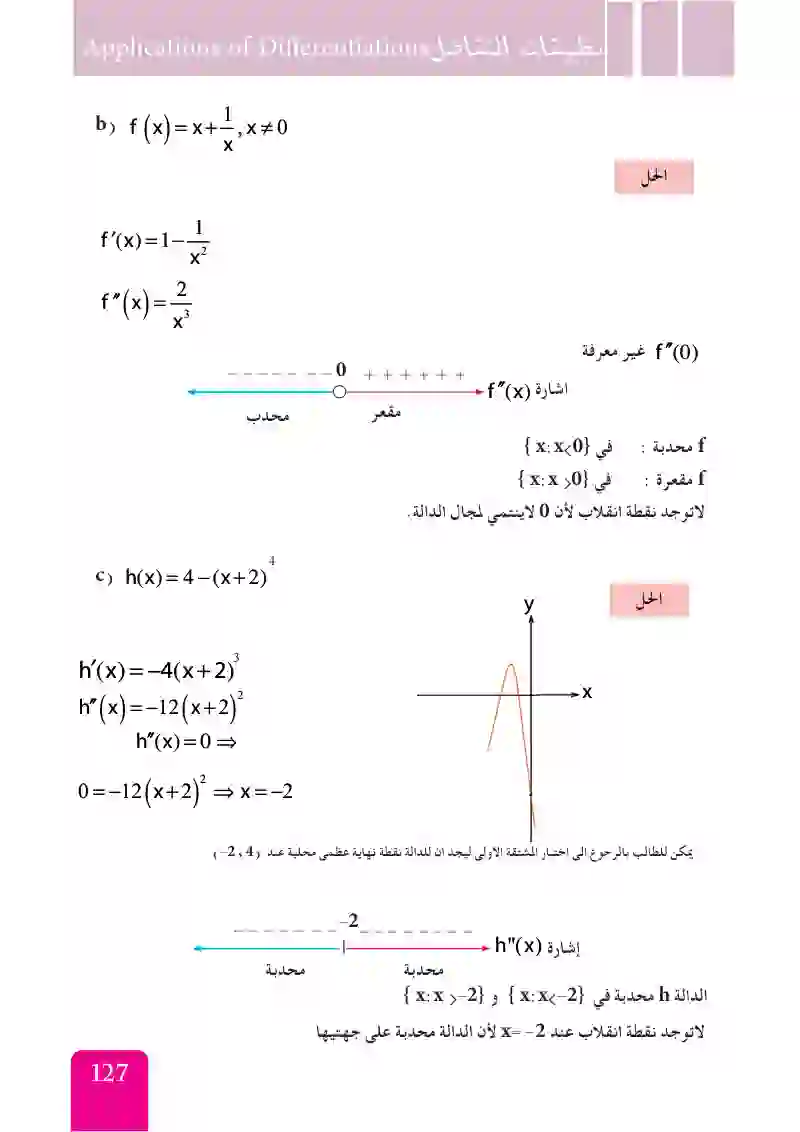
f(x)=x+1/x,x≠0
h(x)=4-(x+2)^4

f(x)=3-2x-x^2
f(x)=x^4+3x^2-3





