مبرهنتا رول والقيمة المتوسطة - الرياضيات العلمي - سادس اعدادي
الفصل الأول: الأعداد المركبة
الفصل الثاني: القطوع المخروطية
الفصل الثالث: تطبيقات التفاضل
الفصل الرابع: التكامل
الفصل الخامس: المعادلات التفاضلية الاعتيادية
الفصل السادس: الهندسة الفضائية

مبرهنتا رول والقيمة المتوسطة
تعريف القيمة المتوسطة

توضيح المبرهنة هندسيا
لتكن f:[-1,1]→R,f(x)=|x|
تعريف النقطة الحرجة

مبرهنة رول
بين هل أن مبرهنة رول تتحقق لكل من الدوال التالية وجد قيمة c الممكنة f(x)=9x+3x^2-x^3,x∈[-1,1]

f(x)=-2(2-x)
f(x)=9x+3x^2-x^3
f(x)=x^2+1,-1
f(x)=k,x∈[a,b]
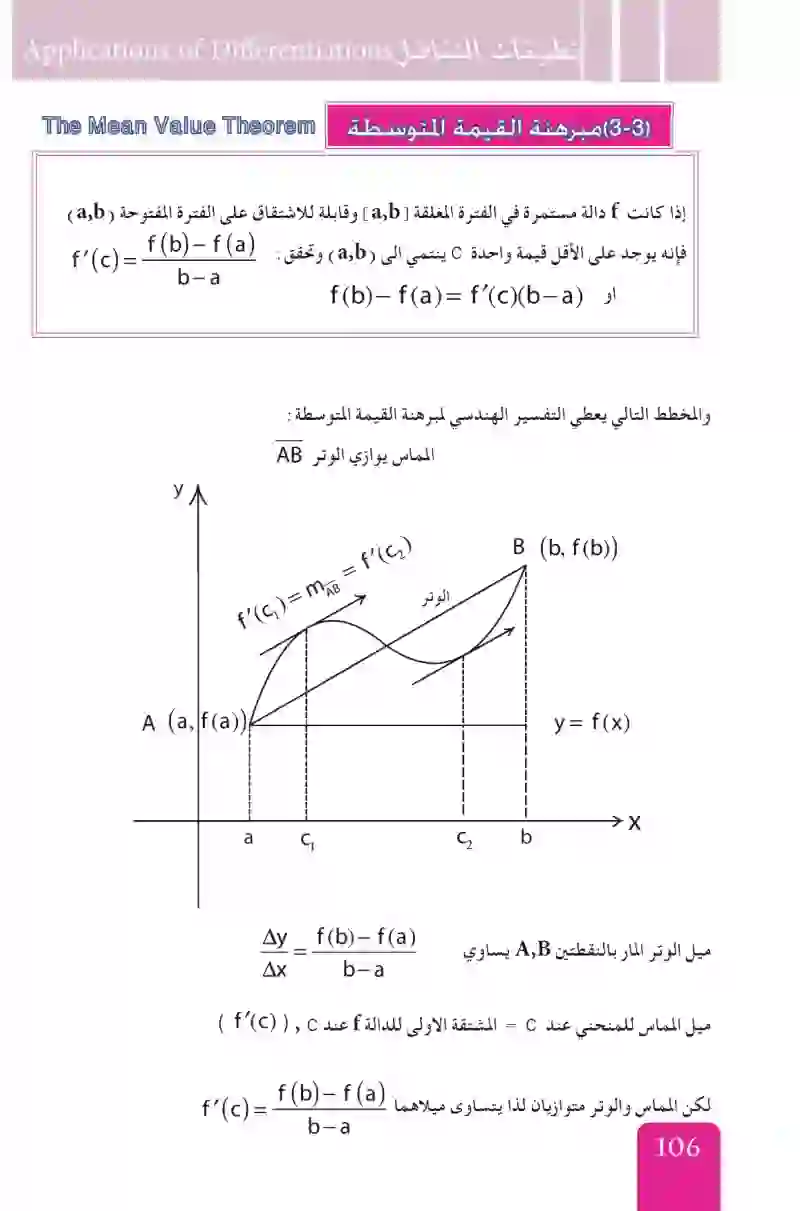
مبرهنة القيمة المتوسطة

مبرهنة رول هي حالة خاصة من مبرهنة القيمة المتوسطة
برهن أن الدوال الآتية تحقق شروط مبرهنة القيمة المتوسطة وأوجد قيم c f(x)=x^2-6x+4,x∈[-1,7]

برهن أن الدوال الآتية تحقق شروط مبرهنة القيمة المتوسطة واوجد قيم C ؟ f(x)=√25-x^2,x∈[-4,0]

إذا كانت f:[0,b]→R,f(x)=x^3-4x^2 وكانت f تحقق مبرهنة القيمة المتوسطة عند c=2/3 فجد قيمة b
نتيجة مبرهنة القيمة المتوسطة

جد باستخدام نتيجة مبرهنة القيمة المتوسطة تقريبا مناسبا للعدد √26

إذا كان f(x)=x^3+3x^2+4x+5 فجد بصورة تقريبية f(1.001)
مكعب طول حرفه 9.98cm جد حجمه بصورة تقريبية باستخدام نتيجة مبرهنة القيمة المتوسطة

لتكن f(x)=∛x^2 فإذا تغيرت x من 8 إلى 8.06 فما مقدار التغير التقريبي للدالة
يراد طلاء مكعب طول ضلعه 10cm فإذا كان سمك الطلاء 0.15cm أوجد حجم الطلاء بصورة تقريبية وباستخدام نتيجة مبرهنة القيمة المتوسطة

باستخدام نتيجة مبرهنة القيمة المتوسطة جد وبصورة تقريبية ومقربا لثلاث مراتب عشرية 5√(0.98)^3+(0.98)^4+3

جد ∛7.8
جد √17+4√17

حل مثال جد √17+4√17
جد ∛0.12

أوجد قيمة c التي تعينها مبرهنة رول في كل مما يأتي f(x)=x^3-9x,x∈[-3,3]
جد تقريبا لكل مما يلي باستخدام نتيجة مبرهنة القيمة المتوسطة √63+∛63
كرة نصف قطرها 6cm طليت بطلاء سمكه 0.1cm جد حجم الطلاء بصورة تقريبية باستخدام نتيجة مبرهنة القيمة المتوسطة
بين أن كل دالة من الدوال التالية تحقق مبرهنة رول على الفترة المعطاة ازاء كل منها ثم جد قيمة c f(x)=(x-1)^4,[-1,3]
اختبر إمكانية تطبيق القيمة المتوسطة للدوال التالية على الفترة المعطاة إزاءها مع ذكر السبب وإن تحققت المبرهنة ، جد قيم c الممكنة f(x)=x^3-x-1,[-1,2]
مخروط دائري قائم ارتفاعه يساوي طول قطر قاعدته فإذا كان ارتفاعه يساوي 2.98cm فجد حجمه بصورة تقريبية باستخدام نتيجة مبرهنة القيمة المتوسطة
كرة حجمها 84∏ cm^3 جد نصف قطرها بصورة تقريبية باستخدام نتيجة القيمة المتوسطة.





