التوزيعات التكرارية - الإحصاء - ثالث ثانوي
الفصل الأول: مبادئ علم الإحصاء
الفصل الثاني: عرض البيانات وتلخيصها
الفصل الثالث: الارتباط والانحدار الخطي
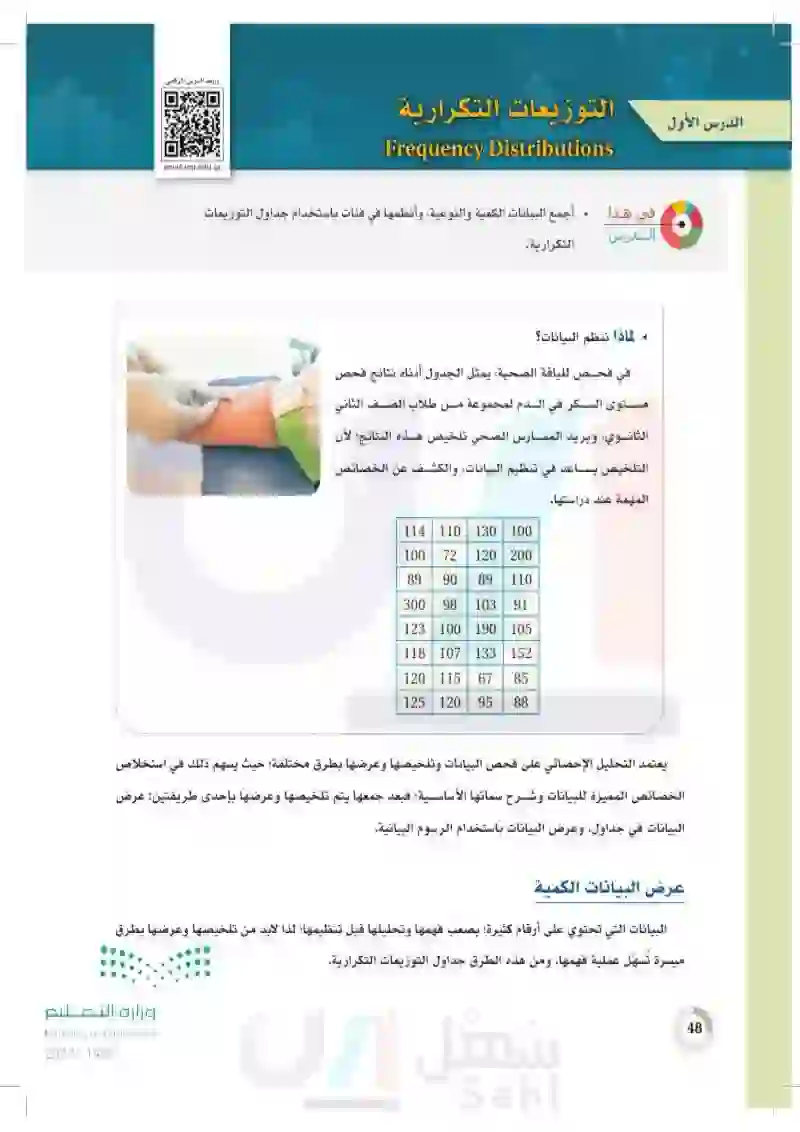
التوزيعات التكرارية الدرس الأول 48 Frequency Distributions رابط الدرس www.ien.edu.sa في هذا . أجمع البيانات الكمية والنوعية، وأنظمها في فئات باستخدام جداول التوزيعات لدرس التكرارية. - لماذا ننظم البيانات؟ في فحص للياقة الصحية، يمثل الجدول أدناه نتائج فحص مستوى السكر في الدم لمجموعة من طلاب الصف الثاني الثانوي، ويريد الممارس الصحي تلخيص هذه النتائج؛ لأن التلخيص يساعد في تنظيم البيانات، والكشف عن الخصائص المهمة عند دراستها. 114 110 100 72 130 100 120 200 89 90 89 110 300 98 103 91 123 100 190 105 118 107 133 18 1 152 120 115 67 85 125 120 95 88 يعتمد التحليل الإحصائي على فحص البيانات وتلخيصها وعرضها بطرق مختلفة؛ حيث يسهم ذلك في استخلاص الخصائص المميزة للبيانات وشرح سماتها الأساسية؛ فبعد جمعها يتم تلخيصها وعرضها بإحدى طريقتين: عرض البيانات في جداول، وعرض البيانات باستخدام الرسوم البيانية. عرض البيانات الكمية البيانات التي تحتوي على أرقام كثيرة؛ يصعب فهمها وتحليلها قبل تنظيمها؛ لذا لابد من تلخيصها وعرضها بطرق ميسرة تُسهل عملية فهمها. ومن هذه الطرق جداول التوزيعات التكرارية. وزارة التعليم Ministry of Education 2024-1446

التوزيعات التكرارية Frequency Distributions
جدول التوزيع التكراري جدول يعرض فئات البيانات مع عدد تكرارها في كل فئة، يرمز حرف (f) إلى عدد تكرار البيانات في الفئة. مكونات جدول التوزيع التكراري الحد الأدنى: يمثل أقل عدد يمكن أن تتضمنه الفئة. الحد الأعلى: يمثل أكبر عدد يمكن أن تتضمنه الفئة. طول الفئة يعني المسافة بين الحدود الدنيا (أو (العليا) للفئات المتتالية. ويمكن حسابه كالآتي: طول الفئة = الحد الأدنى للفئة الثانية - الحد الأدنى للفئة الأولى. المدى هو الفرق بين الحد الأعلى للفئة الأخيرة والحد الأدنى للفئة الأولى. المدى = الحد الأعلى للفئة الأخيرة - الحد الأدنى للفئة الأولى. خطوات إنشاء جدول التوزيع التكراري للبيانات 1. تحديد عدد الفئات المراد تضمينها في التوزيع التكراري يجب أن يكون عدد الفئات بين 5 و 20 كي يسهل التعامل معها). 2 حساب طول الفئة بالطريقة الآتية: تحديد مدى البيانات، قسمة النطاق على عدد الفئات وتقريب الناتج إلى العدد التالي المناسب. 3. حساب حدود الفئات يمكن تحديد القيمة الأقل في البيانات حدًّا أدنى للفئة الأولى. والقيمة الأكبر في البيانات حدا أعلى للفئة الأخيرة. لحساب الحدود الدنيا المتبقية، أضف طول الفئة إلى الحد الأدنى للفئة السابقة، ولحساب الحدود العليا يكون الحد الأعلى للفئة الأولى أقل بمقدار واحد من الحد الأدنى للفئة الثانية، ثم يضاف طول الفئة إلى الحد الأعلى؛ وهكذا لإيجاد حدود الفئات العليا المتبقية. 4 حساب تكرار البيانات في كل فئة. لاحظ: في التوزيع التكراري لا يمكن أن تتداخل الفئات 5 حساب مجموع التكرارات لإيجاد إجمالي التكرار (f) لكل الفئات. ويجب أن تكون أطوالها متساوية. 49 وزارة التعليم Ministry of Education 2024-1446

وزارة التعليم Ministry of Education 2024-1446 1 19 14 8 15 16 26 17 11 10 11 220 22 21 6 17 له 7 18 5 12 17379 18 14 19 22 24 26 25 4 30 2 28 29 1 مثال البيانات المجاورة تمثل درجات الطلاب في مادة اللغة الإنجليزية، أنشئ جدولاً تكراريًا لدرجات الطلاب يحتوي على ست فئات. 6 الحل: 1. عدد الفئات = 2. المدى = أعلى قيمة - أقل قيمة. أقل قيمة في البيانات (1) وأعلى قيمة (30) 1-30 = المدى = 29 طول الفئة = المدى عدد الفئات .3 = 4.835 = 29 6 : طول الفئة 4. يمثل العدد الأصغر (1) في البيانات الحد الأدنى للفئة الأولى، وتكون الحدود الدنيا للفئات الست الأخرى، هي: 1 +5 = 6, 6+5=11, ... وهكذا. 5. يمثل الرقم (5) الحد الأعلى للفئة الأولى، وهو أقل بمقدار واحد من الحد الأدنى للفئة الثانية، وتكون الحدود العليا للفئات الأخرى هي: 5+5=10, 10 + 5 = 15, ... وهكذا. 6. يمثل عدد الدرجات التي تنتمي لكل فئة على حدة تكرار هذه الفئة. على سبيل المثال؛ الدرجات 1,1,2,3,5 في الفئة الأولى (15)، فيكون تكرار هذه الفئة 5. .7. يعبر If عن مجموع تكرارات الفئات. 50

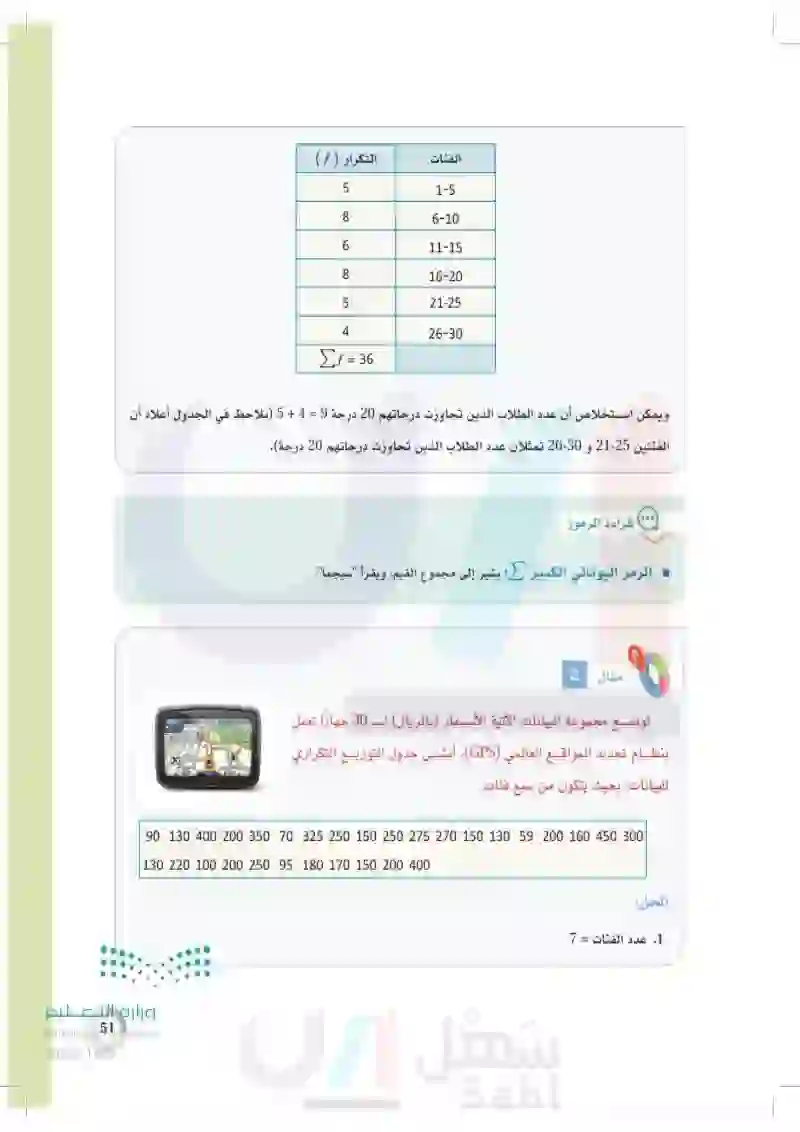
51 وزارة التعليم Ministry of Education 2024-1446 التكرار ( f ) الفئات 5 1-5 8 6-10 6 11-15 8 16-20 5 21-25 4 26-30 If = 36 ويمكن استخلاص أن عدد الطلاب الذين تجاوزت درجاتهم 20 درجة 9 = 4 + 5 نلاحظ في الجدول أعلاه أن الفئتين 25-21 و 300-226 تمثلان عدد الطلاب الذين تجاوزت درجاتهم 20 درجة). GPS 100m Main Rd X City Hall Ave Speed East-Side St 40m Menu NAVIGATION SYSTEM River Park X Arrival 6:51 قراءة الرموز ... الرمز اليوناني الكبير : يشير إلى مجموع القيم، ويقرأ "سيجما". 2 مثال توضح مجموعة البيانات الآتية الأسعار (بالريال) لـ 30 جهازا تعمل بنظام تحديد المواقع العالمي (GPS) ، أنشئ جدول التوزيع التكراري للبيانات؛ بحيث يتكون من سبع فئات. 90 130 400 200 350 70 325 250 150 250 275 270 150 130 59 200 160 450 300 130 220 100 200 250 95 180 170 150 200 400 الحل: 1. عدد الفئات = 7

52 52 2. المدى = أعلى قيمة – أقل قيمة. أقل قيمة في البيانات (59) وأعلى قيمة (450). 59 - 450 = المدى .3 المدى عدد الفئات = طول الفئة = 55.8656 391 == 7 = طول الفئة = 391 .4 يمثل العدد الأصغر (59) في البيانات الحد الأدنى للفئة الأولى، وتكون الحدود الدنيا للفئات الست الأخرى، هي: 5956115, 115+ 56 = 171, ... وهكذا. 5. يمثل الرقم (114) الحد الأعلى للفئة الأولى، وهو أقل بمقدار واحد من الحد الأدنى للفئة الثانية، وتكون الحدود العليا للفئات الأخرى هي: 114 +56 = 170, 170+56=226, .. وهكذا. 6. يمثل عدد الأسعار التي تنتمي لكل فئة على حدة تكرار هذه الفئة. على سبيل المثال؛ الأسعار 90, 70, 59, 100, 990 في الفئة الأولى (114-59)، فيكون تكرار هذه الفئة 5. 7. يعرض الجدول الآتي التوزيع التكراري للبيانات ويعبر عن مجموع التكرارات: الفئات التكرار ( f ) 5 59-114 8 115-170 6 171-226 5 227-282 2 283-338 1 339-394 3 395-450 If = 30 : وزارة التعليم Ministry of Education 2024-1446

تحقق من فهمك 1 تمثل البيانات الآتية أعمار عدد من المخترعين الذين نالوا براءات اختراع عام 2009م 29 89 87 86 86 85 83 82 81 83 69 68 67 66 66 65 65 64 63 80 78 78 77 76 73 73 73 72 69 61 61 60 59 58 57 56 54 54 53 53 51 51 49 47 46 44 43 42 36 35 قسم البيانات السابقة إلى ثمان فئات، ثم أنشئ توزيعًا تكراريًا لهذه البيانات. ماذا تلاحظ على مجموع التكرارات (f)؟ من جدول التوزيع التكراري يمكن إيجاد مركز الفئة والتكرار النسبي، والتكرار التراكمي لكل فئة. مركز الفئة القيمة التي تتوسط الفئة. ويمكن إيجاده باستخدام القانون الآتي: مركز الفئة = الحد الأعلى للفئة + الحد الأدنى للفئة التكرار النسبي للفئة 2 تكرار الفئة (أ) مقسومًا على مجموع التكرارات )) . ويمكن إيجاده باستخدام القانون الآتي: التكرار النسبي = تكرار الفئة (f) مجموع التكرارات (f) يمكن كتابة التكرار النسبي في صورة كسر أو عدد عشري أو نسبة مئوية، ويجب أن يكون مجموع التكرارات النسبية لجميع الفئات مساويًا لـ 1 أو %100. التكرار التراكمي للفئة مجموع تكرارات هذه الفئة والفئات التي قبلها. الحدود الحقيقية للفئة لكل فئة حدان حقيقيان حد أدنى حقيقي، وحد أعلى حقيقي. ويمكن حساب الحد الأدنى الحقيقي والحد الأعلى الحقيقي كالآتي: الحد الأدنى الحقيقي= الحد الأدنى - 0.5 الحد الأعلى الحقيقي= الحد الأعلى + 0.5 53 333 وزارة التعليم Ministry of Education 2024-1446

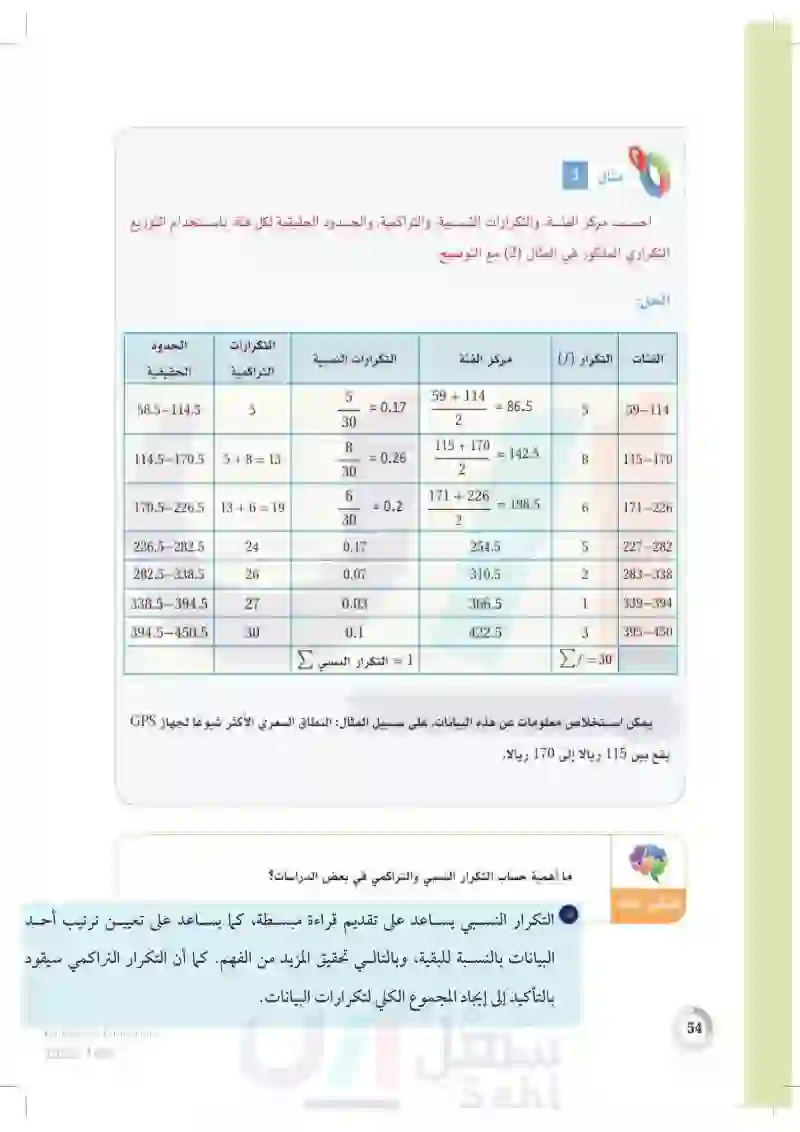
54 مثال 3 احسب مركز الفئة والتكرارات النسبية والتراكمية والحدود الحقيقية لكل فئة، باستخدام التوزيع التكراري المذكور في المثال (2) مع التوضيح. الحل: الفئات التكرار (f) مركز الفئة التكرارات النسبية التكرارات التراكمية الحدود الحقيقية 5 58.5-114.5 5 = 0.17 30 59 + 114 2 = 86.5 5 LO 59-114 8 114.5-170.5 5+8=13 = 0.26 30 115 + 170 2 = 142.5 8 115-170 6 171 +226 170.5-226.5 13+ 6 = 19 = 0.2 = 198.5 6 171-226 30 2 226.5-282.5 24 0.17 254.5 5 227-282 282.5-338.5 26 0.07 310.5 2 283-338 338.5-394.5 27 0.03 366.5 1 339-394 394.5-450.5 30 0.1 422.5 3 395-450 1 = التكرار النسبي 2 =1 If = 30 يمكن استخلاص معلومات عن هذه البيانات، على سبيل المثال : النطاق السعري الأكثر شيوعًا لجهاز GPS يقع بين 115 ريالا إلى 170 ريالا. ما أهمية حساب التكرار النسبي والتراكمي في بعض الدراسات؟ تفكير ناقد وزارة التعليم Ministry of Education 2024-1446

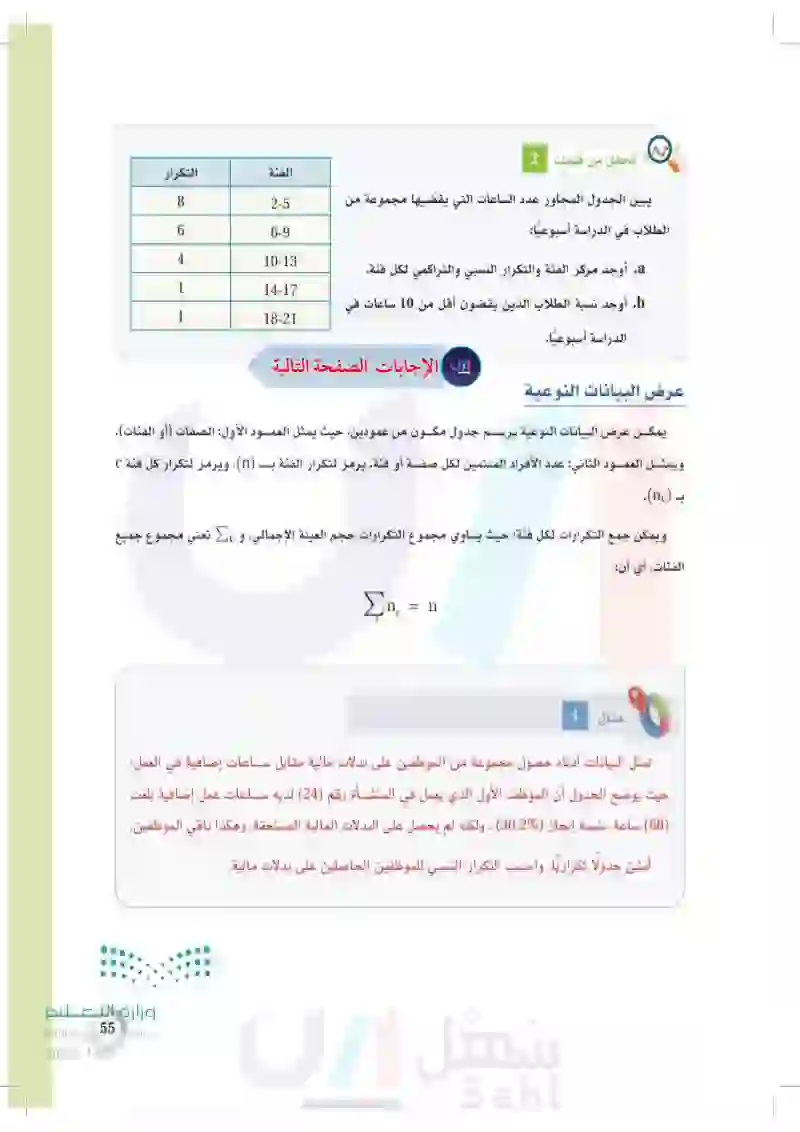
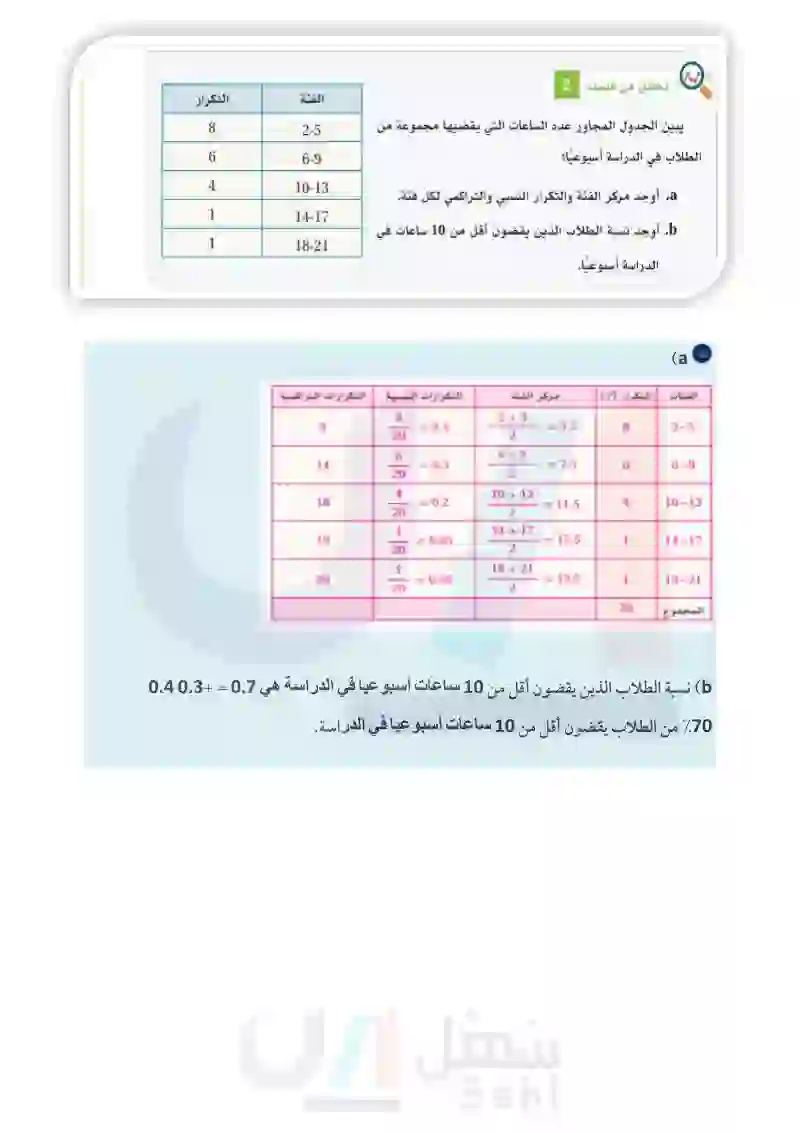
تحقق من فهمك 2 الفئة التكرار يبين الجدول المجاور عدد الساعات التي يقضيها مجموعة من الطلاب في الدراسة أسبوعيًا: a. أوجد مركز الفئة والتكرار النسبي والتراكمي لكل فئة. b أوجد نسبة الطلاب الذين يقضون أقل من 10 ساعات في الدراسة أسبوعيًا. عرض البيانات النوعية 8 2-5 6 6-9 4 10-13 1 14-17 1 18-21 يمكن عرض البيانات النوعية برسم جدول مكون من عمودين، حيث يمثل العمود الأول: الصفات أو الفئات) ويمثل العمود الثاني: عدد الأفراد المنتمين لكل صفة أو فئة يرمز لتكرار الفئة بـ (n) ، ويرمز لتكرار كل فئة C بـ (nc). ويمكن جمع التكرارات لكل فئة؛ حيث يساوي مجموع التكرارات حجم العينة الإجمالي، و لا تعني مجموع جميع الفئات، أي أن: مثال 4 Ση = n C C تمثل البيانات أدناه حصول مجموعة من الموظفين على بدلات مالية مقابل ساعات إضافية في العمل؛ حيث يوضح الجدول أن الموظف الأول الذي يعمل في المنشأة رقم (24) لديه ساعات عمل إضافية بلغت (68) ساعة، بنسبة إنجاز (30.2) ، ولكنه لم يحصل على البدلات المالية المستحقة وهكذا باقي الموظفين. أنشئ جدولاً تكراريًّا، واحسب التكرار النسبي للموظفين الحاصلين على بدلات مالية. 55 55 وزارة التعليم Ministry of Education 2024-1446

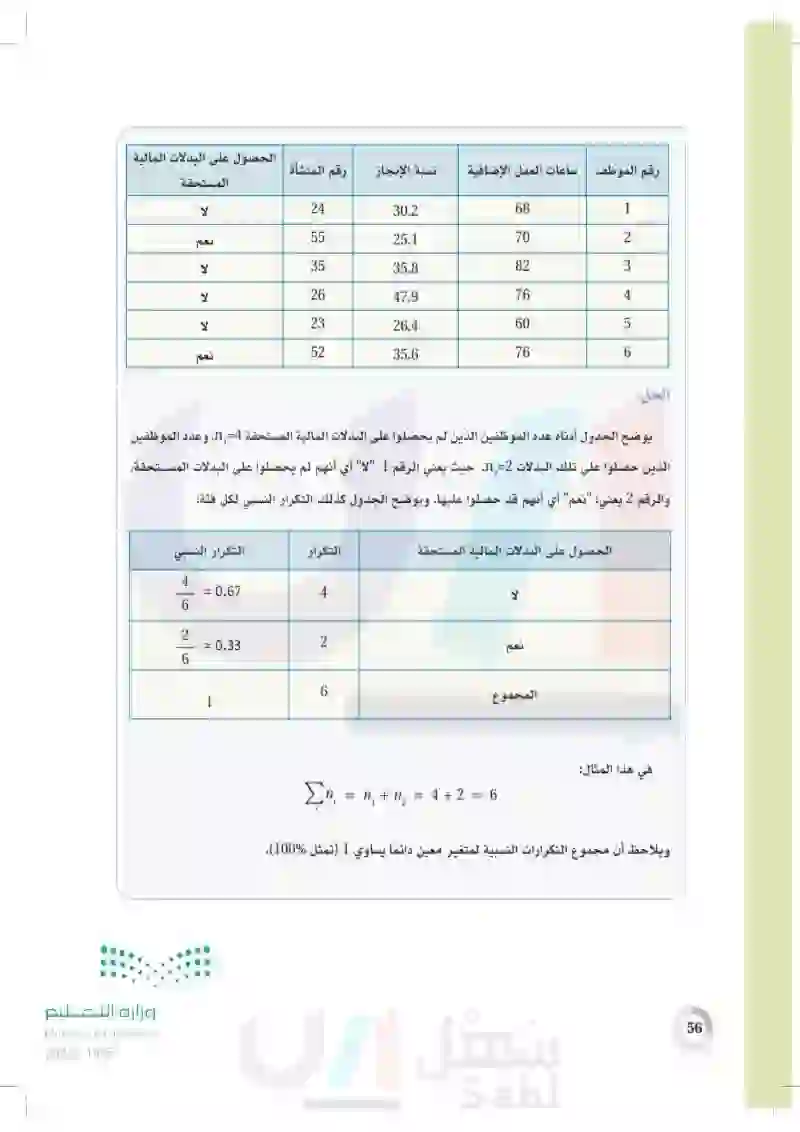
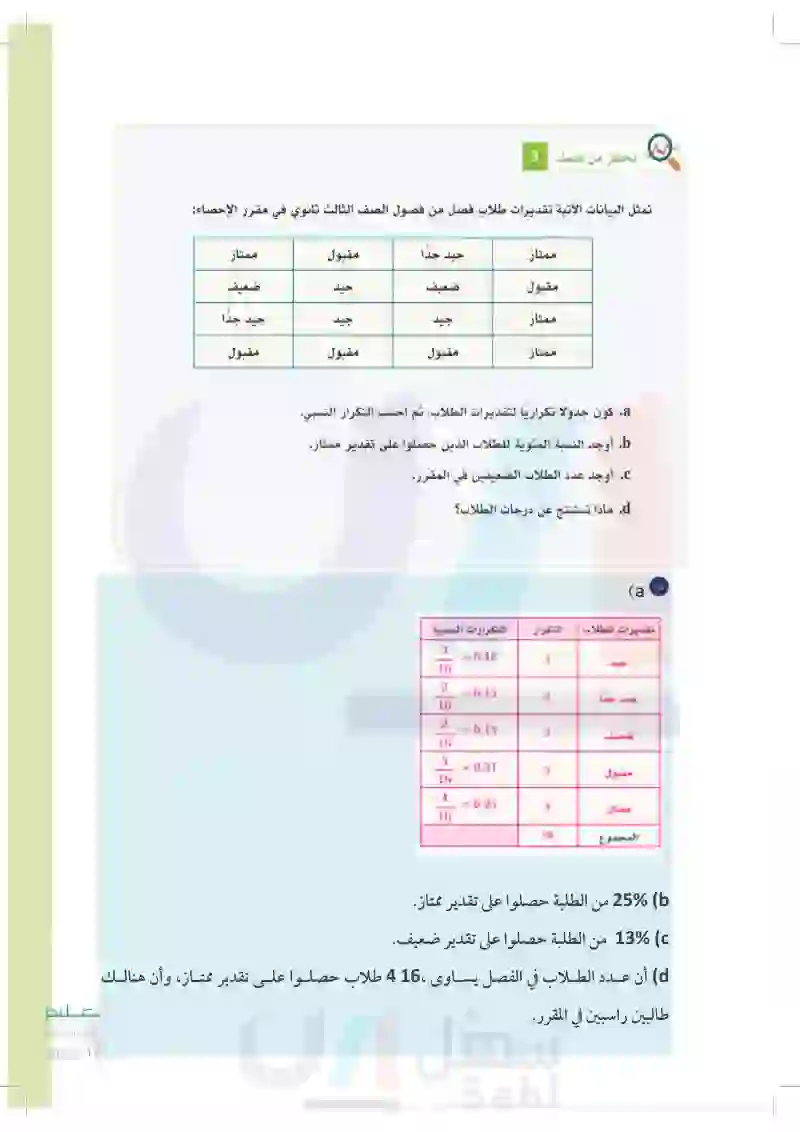
56 رقم الموظف ساعات العمل الإضافية نسبة الإنجاز رقم المنشأة 24 30.2 68 1 55 25.1 70 2 35 35.8 82 3 26 47.9 76 4 23 26.4 60 LO 5 52 35.6 76 6 الحصول على البدلات المالية المستحقة لا نعم لا نعم الحل: يوضح الجدول أدناه عدد الموظفين الذين لم يحصلوا على البدلات المالية المستحقة 4 n، وعدد الموظفين الذين حصلوا على تلك البدلات 12 حيث يعني الرقم 1 "لا" أي أنهم لم يحصلوا على البدلات المستحقة، والرقم 2 يعني: "نعم" أي أنهم قد حصلوا عليها. ويوضح الجدول كذلك التكرار النسبي لكل فئة: الحصول على البدلات المالية المستحقة في هذا المثال: نعم المجموع التكرار التكرار النسبي 4 = 0.67 4 6 2 = 0.33 2 6 6 1 Ση n = C = n + n = 4 + 2 = 6 C ويلاحظ أن مجموع التكرارات النسبية لمتغير معين دائمًا يساوي 1 (تمثل %100). وزارة التعليم Ministry of Education 2024-1446

56 رقم الموظف ساعات العمل الإضافية نسبة الإنجاز رقم المنشأة 24 30.2 68 1 55 25.1 70 2 35 35.8 82 3 26 47.9 76 4 23 26.4 60 LO 5 52 35.6 76 6 الحصول على البدلات المالية المستحقة لا نعم لا نعم الحل: يوضح الجدول أدناه عدد الموظفين الذين لم يحصلوا على البدلات المالية المستحقة 4 n، وعدد الموظفين الذين حصلوا على تلك البدلات 12 حيث يعني الرقم 1 "لا" أي أنهم لم يحصلوا على البدلات المستحقة، والرقم 2 يعني: "نعم" أي أنهم قد حصلوا عليها. ويوضح الجدول كذلك التكرار النسبي لكل فئة: الحصول على البدلات المالية المستحقة في هذا المثال: نعم المجموع التكرار التكرار النسبي 4 = 0.67 4 6 2 = 0.33 2 6 6 1 Ση n = C = n + n = 4 + 2 = 6 C ويلاحظ أن مجموع التكرارات النسبية لمتغير معين دائمًا يساوي 1 (تمثل %100). وزارة التعليم Ministry of Education 2024-1446