تصنيف المثلثات - رياضيات 1-2 - أول ثانوي

www.ien.edu.sa تصنيف المثلثات Classifying triangles 3-1 فيما سبق: درست قياس الزوايا وتصنيفها. (مهارة سابقة) والآن أستعمل تصنيف المثلثات وفقًا لأضلاعها أو زواياها في إيجاد قيم مجهولة. المفردات: المثلث الحاد الزوايا acute triangle المثلث المنفرج الزاوية obtuse triangle المثلث القائم الزاوية right triangle لماذا؟ يعد المثلث عنصرًا زخرفيًا مميزا في العمارة التقليدية في المملكة العربية السعودية، كما يلاحظ ذلك في صالات المسافرين بمطار الملك خالد الدولي بمدينة الرياض. تصنيف المثلثات وفقًا لزواياها يكتب المثلث ABC على الصورة AABC ، وتُسمى عناصره باستعمال الأحرف A B C كما يلي: أضلاع ABC هي : AB, C, CA . الرؤوس هي : ABC الزوايا هي: LA أو BAC أو BBC أو ABC C B وتُصنف المثلثات بطريقتين وفقًا لزواياها أو أضلاعها. وتحتوي جميع المثلثات على زاويتين حادتين على المثلث المتطابق الأضلاع الأقل، وتُستعمل الزاوية الثالثة لتصنيف المثلث. equilateral triangle ل مفهوم أساسي المثلث المتطابق الضلعين isosceles triangle المثلث المختلف الأضلاع أضف إلى مطويتك تصنيف المثلثات وفقًا لزواياها مثلث حاد الزوايا مثلث منفرج الزاوية مثلث قائم الزاوية A 3 زوايا حادة إحدى الزوايا منفرجة إحدى الزوايا قائمة يمكن تصنيف أي مثلث وفقًا لزواياه إلى أحد التصنيفات السابقة، بمعرفة قياسات زواياه. مثال 1 تصنيف المثلثات وفقًا لزواياها صنف كلا من المثلثين الآتيين وفقا لزواياه: 90° 30° 60° 70 40° 70° زوايا المثلث الثلاث حادة؛ لذا فالمثلث حاد الزوايا. قياس إحدى زوايا هذا المثلث 90 ، وبما أن إحدى زواياه قائمة، فإنه مثلث قائم الزاوية. وزارة التعليم Ministry of Education 2024-1446 scalene triangle الفصل 3 المثلثات المتطابقة 12 12

تصنيف المثلثات وفقاً لزواياها

صنف كلا من المثلثين الآتيين وفقا لزواياه

أستعمل تصنيف المثلثات وفقا لأضلاعها أو زواياها في إيجاد قيم مجهولة

(18) 60° 60° 60° تحقق من فهمك صنف كلا من المثلثين الآتيين وفقا لزواياه: 97° 49° 34° (1A مثال 2 تصنيف المثلثات ضمن أشكال مختلفة وفقًا لزواياها صنف APQR إلى حاد الزوايا أو متطابق الزوايا أو منفرج الزاوية أو قائم الزاوية: النقطة S داخل PQR ، وحسب مسلّمة جمع قياسات الزوايا تقع يكون : mZPQR = mZPQS + m2SQR بالتعويض : 104 = 59 + 45 = mZPQR وبما أن إحدى زوايا APQR منفرجة، فإنه منفرج الزاوية. تحقق من فهمك Q 45° 59° 45° 31° P S R (2) استعمل الشكل أعلاه لتصنيف APQS إلى حاد الزوايا أو متطابق الزوايا أو منفرج الزاوية أو قائم الزاوية. تصنيف المثلثات وفقًا لأضلاعها يمكن كذلك تصنيف المثلثات بحسب عدد الأضلاع المتطابقة فيها. وللدلالة على تطابق ضلعين في مثلث، يوضع عدد متساو من الشرطات الصغيرة على الضلعين المتطابقين. مفهوم أساسي مثلث متطابق الأضلاع تصنيف المثلثات وفقا لأضلاعها مثلث متطابق الضلعين أضف إلى مطويتك مثلث مختلف الأضلاع مراجعة المفردات الزاوية الحادة: زاوية يقل قياسها عن 90 الزاوية القائمة: زاوية قياسها 90 الزاوية المنفرجة : زاوية قياسها أكبر من 90 2cm 2cm 2cm الربط مع الحياة في العديد من السيارات تشغل أضواء الخطر بالضغط على زر صغير قرب المقود يكون شكل هذا الزر عادة مثلثا أحمر أو برتقاليا صغيرا كما في الشكل أعلاه. 3 أضلاع متطابقة ضلعان على الأقل متطابقان لا توجد أضلاع متطابقة إن المثلث المتطابق الأضلاع حالة خاصة من المثلث المتطابق الضلعين. مثال 3 من واقع الحياة تصنيف المثلثات وفقًا لأضلاعها فن العمارة: صنّف المثلث في الشكل المجاور وفقا لأضلاعه. عندما يشغل هذا الزر تضيء في المثلث ضلعان قياس كل منهما 55cm ؛ أي أنه في المثلث ضلعين متطابقين. فيكون المثلث متطابق الضلعين أضواء إشارات الانعطاف بطريقة تحذيرية وبنمط خاص يسهل رؤية السيارة من قبل السائقين الآخرين. تحقق من فهمك 55cm 55cm 45cm 3) قيادة السيارة والسلامة صنف شكل زرّ ضوء الخطر في الهامش يمين الصفحة وفقًا لأضلاعه. الدرس 1-3 - تصنيف المثلثات الت13 Ministry of E 2024-1446

تحقق من فهمك1 صنف كلا من المثلثين الآتيين وفقاً لزواياه

تصنيف المثلثات ضمن أشكال مختلفة وفقاً لزواياها

تصنيف المثلثات وفقاً لأضلاعها

صنف المثلث في الشكل المجاور وفقا لأضلاعه

الزاوية الحادة، الزاوية القائمة، الزاوية المنفرجة

استعمل الشكل اعلاه لتصنيف المثلث PQS إلى حاد الزوايا او متطابق الزوايا او منفرج الزوايا او قائم الزاوية

صنف شكل زر ضوء الخطر في الهامش يمين الصفحة وفقا لأضلاعه

في العديد من السيارات تشغل اضواء الخطر بالضغط على زر صغير قرب المقود

K 1.3. L 0.75 M مثال 4 تصنيف المثلثات ضمن أشكال مختلفة وفقًا لأضلاعها إذا كانت M نقطة منتصف JL ، فصنف AJKM إلى متطابق الأضلاع أو متطابق الضلعين أو مختلف الأضلاع. ووضّح إجابتك. من تعريف نقطة المنتصف JM = ML مسلمة جمع قياسات القطع المستقيمة عوض بسط اقسم الطرفين على 2 JM + ML = JL ML + ML = 1.5 2ML = 1.5 ML = 0.75 JM = ML = 0.75 وبما أن KM = ML ، فإن 0.75 = KM = ML وهكذا تكون قياسات أضلاع المثلث الثلاثة متساوية، أي أن الأضلاع الثلاثة متطابقة؛ لذا فإن المثلث متطابق الأضلاع. تحقق من فهمك 4) صنف AKML إلى متطابق الأضلاع أو متطابق الضلعين أو مختلف الأضلاع. ووضّح إجابتك. يمكنك استعمال خصائص المثلثات المتطابقة الأضلاع والمتطابقة الضلعين؛ لإيجاد قيم مجهولة كما في المثال الآتي : مثال 5 إيجاد قيم مجهولة جبر أوجد قياسات أضلاع المثلث المتطابق الضلعين ABC في الشكل المجاور. الخطوة 1 أوجد قيمة X. 9x - 1 A B 4x+1 5x−0.5 C وزارة التعليم Ministry of Education 2024-1446 F 2y+5 5y-19 G H 3y-3 معطى عوض اطرح 4x من الطرفين اجمع 0.5 إلى الطرفين AC = CB 4x + 1 = 5x - 0.5 1 = x - 0.5 1.5 = x إرشادات للدراسة تحقق للتحقق من الإجابة في المثال 5 ، اختبر ما إذا كانت CB = AC عندما نعوض بـ 1.5 مكان x في العبارة 0.5 - 5x التي تمثل CB الخطوة 2 عوّض لإيجاد طول كل ضلع من أضلاع المثلث : معطى معطى x = 1.5 AC = 7 x = 1.5 AC = 4x + 1 4(1.5)+17 CB = AC AB = 9x - 1 = 7 9(1.5) 1 = 12.5 معطى مسطر تحقق من فهمك 5) أوجد قياسات أضلاع المثلث المتطابق الأضلاع FGH CB = 5x - 0.5 5(1.5) 0.5 =7✓ الفصل 3 المثلثات المتطابقة 14

تصنيف المثلثات ضمن أشكال مختلفة وفقا لأضلاعها

إيجاد قيم مجهولة

صنف المثلث KML إلى متطابق الأضلاع او متطابق الضلعين او مختلف الاضلاع ووضح اجابتك

للتحقق من الاجابة في المثال 5 اختبر ما إذا كانت CB=AC عندما نعوض ب 1.5 مكان x

أوجد قياسات أضلاع المثلث المتطابق الأضلاع FGH

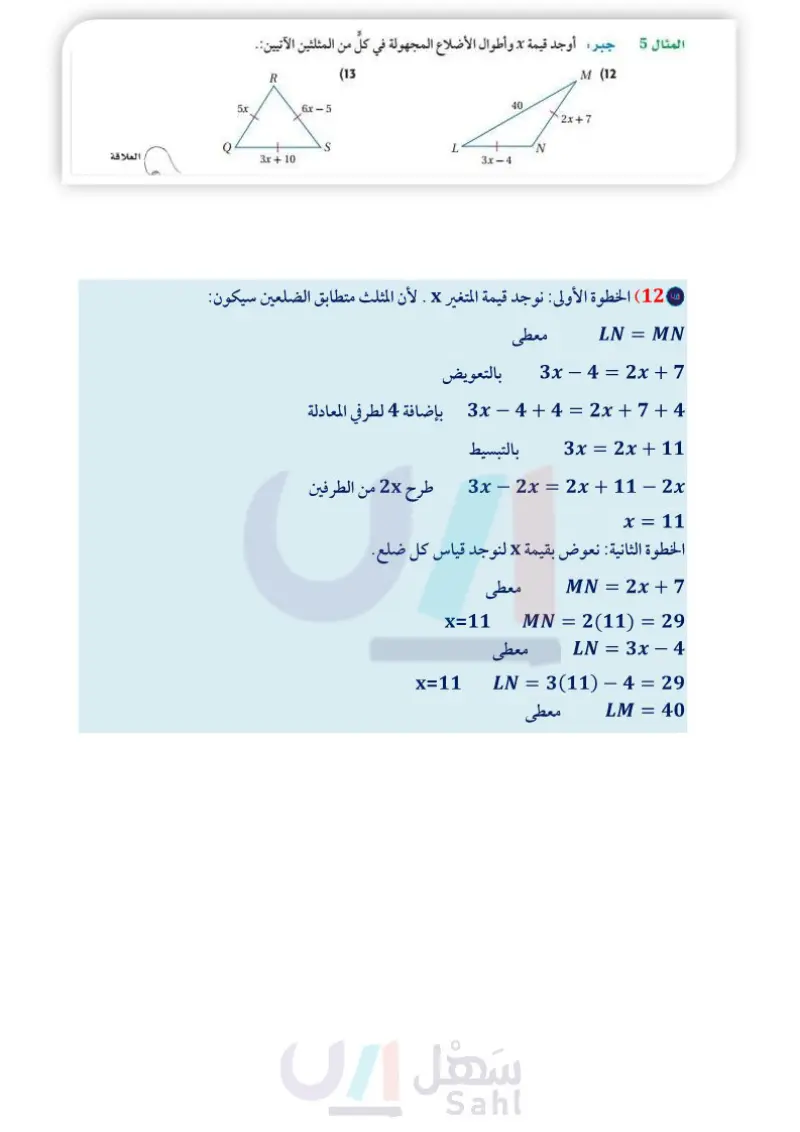
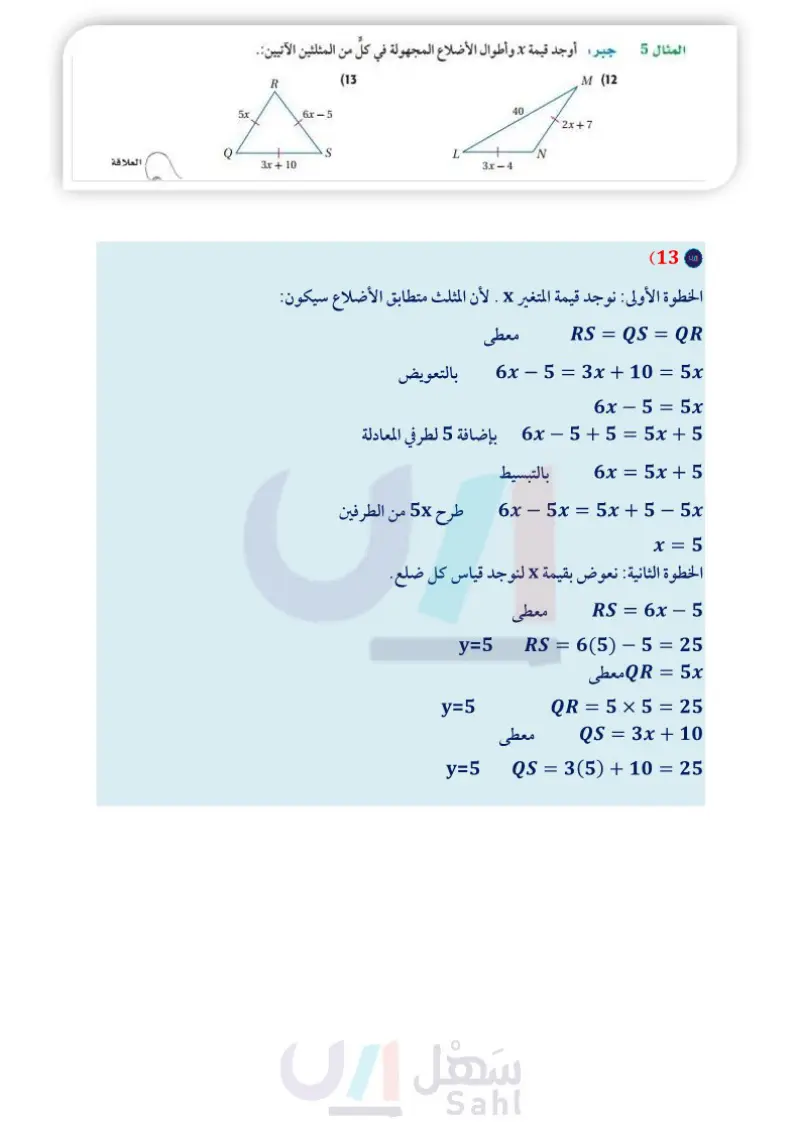
60° (3 130° المثال 1 فن العمارة : صنف كلا من المثلثات الآتية وفقا لزواياه. (2 60° 25 25° 60° 90° 60' D 60/120' 30 5 60% 30 B G 8 12 cm K 2.5 H 5 3 7 L العلاقة 4.x-0.8 3x+0.2 2x+0.1 13 cm 5.x .5cm (8 (1 المثال 2 صنف كلا من المثلثات الآتية وفقا لزواياه. AABD 4 ABDC (5 AABC (6 المثال 3 صنف كلا من المثلثين الآتيين وفقا لأضلاعه. (7 المثال 4 إذا كانت النقطة K هي منتصف FH ، فصنف كلا من المثلثات الآتية في الشكل المجاور إلى متطابق الأضلاع أو متطابق الضلعين أو مختلف الأضلاع R AFGH (9 AGIL (10 AFHL (11 جبر أوجد قيمة x وأطوال الأضلاع المجهولة في كلِّ من المثلثين الآتي 6x-5 S 3x + 10 (13) M (12 40 2x+7 L N 3x-4 (14) مجوهرات افترض أن لديك سلكا مرنا من الفولاذ غير قابل للصدأ، وتريد أن تُشكّله لتعمل قرطًا. إذا كان الجزء المثلث من القرط متطابق الضلعين، وأبعاده كما في الصورة، وطول جزء العلاقة cm 1.5، فكم سنتمترًا من السلك تحتاج لعمل القرط ؟ برر إجابتك. الدرس 1-3 - تصنيف المثلثات الت15 Ministry of Ed 2024-1446 المثال 5 تأكد

تأكد مثال 1 صنف كل من المثلثات الآتية وفقاً لزواياه

تاكد مثال2 صنف كلاً من المثلثات الآتية وفقا لزواياه

تأكد مثال 3 صنف كلاً من المثلثين الآتيين وفقاً لأضلاعه

صنف كلاً من المثلثات الآتية في الشكل المجاور الى متطابق الاضلاع او متطابق الضلعين او مختلف الأضلاع

أوجد قيمة x وأطوال الأضلاع المجهولة في كل من المثلثين الآتيين

كم سنتمترا من السلك تحتاج لعمل القرط؟ برر اجابتك

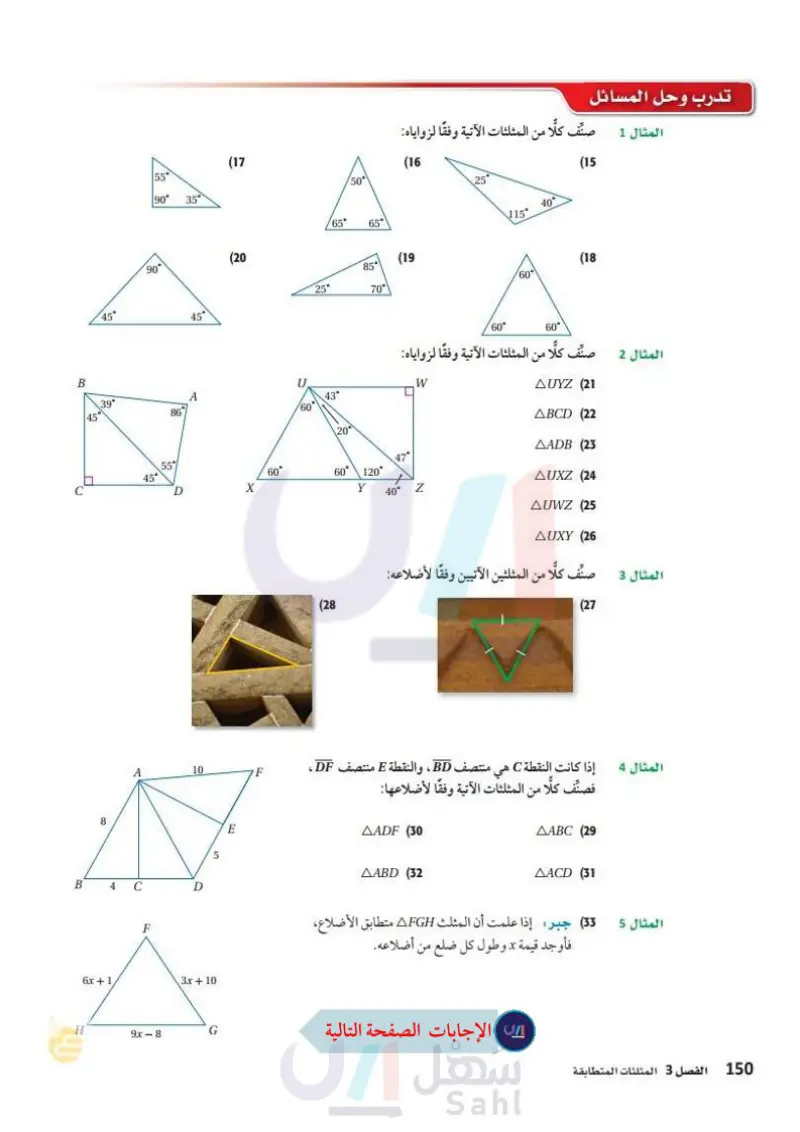
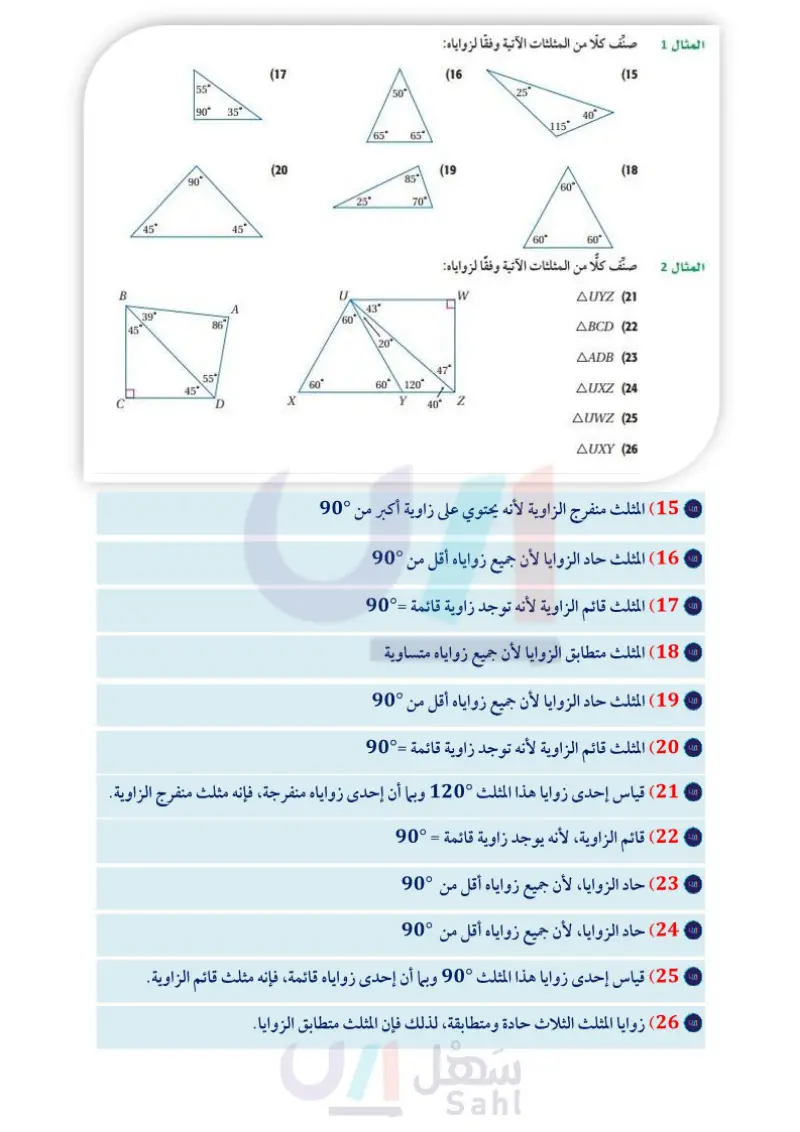
B B 45 55' 90° 35° تدرب وحل المسائل صنف كلا من المثلثات الآتية وفقا لزواياه: المثال 1 (17 (16 /50° 25' (15 40° 115 /65° 65° (20 90° 85° (19 (18 60° 25° 70° 45° 60° 60° صنف كلًا من المثلثات الآتية وفقا لزواياه: المثال 2 U .W A 43° 39 60° 45° 86 20° AUYZ (21 ABCD 22 AADB (23 47° 55 60° 60° 120° 45 AUXZ (24 D X Y 40° Z AUWZ (25 AUXY (26) 8 4 10 F C D 5 6x+1. F 3x + 10 A ...H 9x-8 G وزارة التعليم Ministry of Education 2024-1446 (28 المثال 3 صنف كلا من المثلثين الآتيين وفقا لأضلاعه: (27 المثال 4 إذا كانت النقطة C . اهي منتصف BD ، والنقطة E منتصف DF، فصنف كلا من المثلثات الآتية وفقا لأضلاعها : AADF (30) ABD 32 AABC (29 AACD 31 (33) جبر إذا علمت أن المثلث AFGH متطابق الأضلاع، فأوجد قيمة x وطول كل ضلع من أضلاعه. المثال 5 الفصل 3 المثلثات المتطابقة 16

تدرب مثال 1 صنف كل من المثلثات الآتية وفقاً لزواياه

تدرب مثال2 صنف كلاً من المثلثات الآتية وفقا لزواياه

تدرب مثال 3 صنف كلاً من المثلثين الآتيين وفقاً لأضلاعه

تدرب مثال4 صنف كلاً من المثلثات الآتية وفقاً لأضلاعها

أوجد قيمة x وطول كل ضلع من أضلاعه

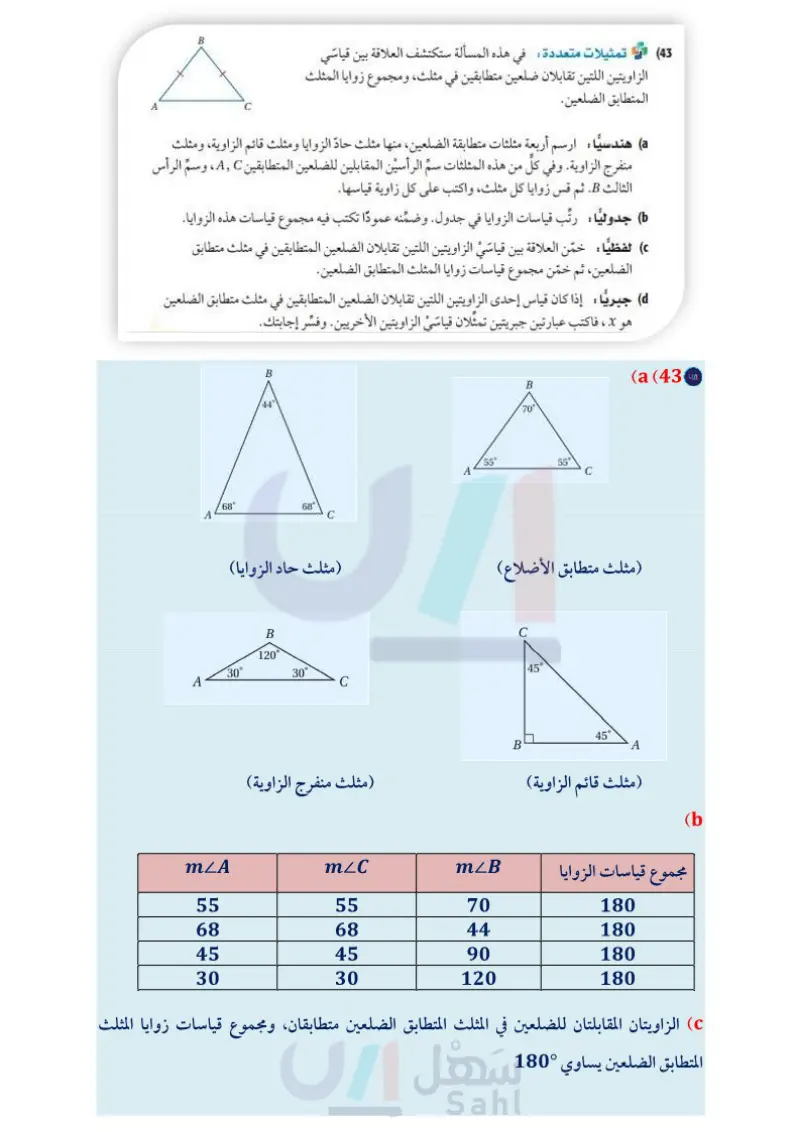
5 A B 75° 34) فن تشكيلي: صنف كلا من المثلثات المرقمة في الشكل وفق زواياه ثم وفق أضلاعه، استعمل المثلث القائم الزاوية لتصنيف الزوايا، والمسطرة لقياس الأضلاع صنف كلا من المثلثات الظاهرة في الشكل المجاور وفق زواياه، 75 ABDC (37 AEBC (36 C E D 15° 15° ثم وفق أضلاعه AABE (35 هندسة إحداثية : أوجد أطوال أضلاع AXYZ في كلُّ من السؤالين الآتيين، وصنفه وفق أضلاعه: X(-5, 9), (2, 1), Z(-8, 3) (38 X(7, 6), Y(5, 1), Z(9, 1) (39 (40) برهان اكتب برهانا ذا عمودين تبين فيه أنّ ABCD متطابق الزوايا، إذا كان AACE متطابق الزوايا، وكانت BD || AE . C B D E جبر أوجد قيمة x وأطوال أضلاع المثلث في كل مما يأتي: 41) AFGH مثلث متطابق الأضلاع فيه : 120 + FG = 3x – 10, GH = 2x + 15 HF = x . (42) ARST متطابق الأضلاع. ويزيد RS ثلاثة على أربعة أمثال x ، ويزيد ST سبعة على مثلي x ، ويزيد TR واحدًا على خمسة أمثال x . (43) تمثيلات متعددة في هذه المسألة ستكتشف العلاقة بين قياسي الزاويتين اللتين تقابلان ضلعين متطابقين في مثلث، ومجموع زوايا المثلث المتطابق الضلعين. C B A هندسيا : ارسم أربعة مثلثات متطابقة الضلعين، منها مثلث حادّ الزوايا ومثلث قائم الزاوية، ومثلث منفرج الزاوية. وفي كل من هذه المثلثات سم الرأسين المقابلين للضلعين المتطابقين ، وسم الرأس الثالث .B. ثم قس زوايا كل مثلث، واكتب على كل زاوية قياسها. جدوليا : رتب قياسات الزوايا في جدول وضمنه عمودًا تكتب فيه مجموع قياسات هذه الزوايا. لفظيا : خمّن العلاقة بين قياسي الزاويتين اللتين تقابلان الضلعين المتطابقين في مثلث متطابق الضلعين، ثم خمّن مجموع قياسات زوايا المثلث المتطابق الضلعين. جبريًا : إذا كان قياس إحدى الزاويتين اللتين تقابلان الضلعين المتطابقين في مثلث متطابق الضلعين هو X ، فاكتب عبارتين جبريتين تمثلان قياسي الزاويتين الأخريين. وفسّر إجابتك. الدرس 1-3- تصنيف المثلثات الت17 Ministry of Educat 2024-1446

استعمل المثلث القائم الزاوية لتصنيف الزوايا والمسطرة لقياس الاضلاع

صنف كلا من المثلثات الظاهرة في الشكل المجاور وفق زواياه ثم وفق اضلاعه

اوجد أطوال أضلاع المثلث XYZ في كل من السؤاليين الآتيين وصنفه وفق أضلاعه

اكتب برهانا ذا عمودين تبين فيه ان المثلث BCD متطابق الزوايا

أوجد قيمة x وأطوال أضلاع المثلث في كل مما يأتي

أرسم اربعة مثلثات متطابقة الضلعين منها مثلث حاد الزوايا ومثلث قائم الزاوية ومثلث منفرج الزاوية

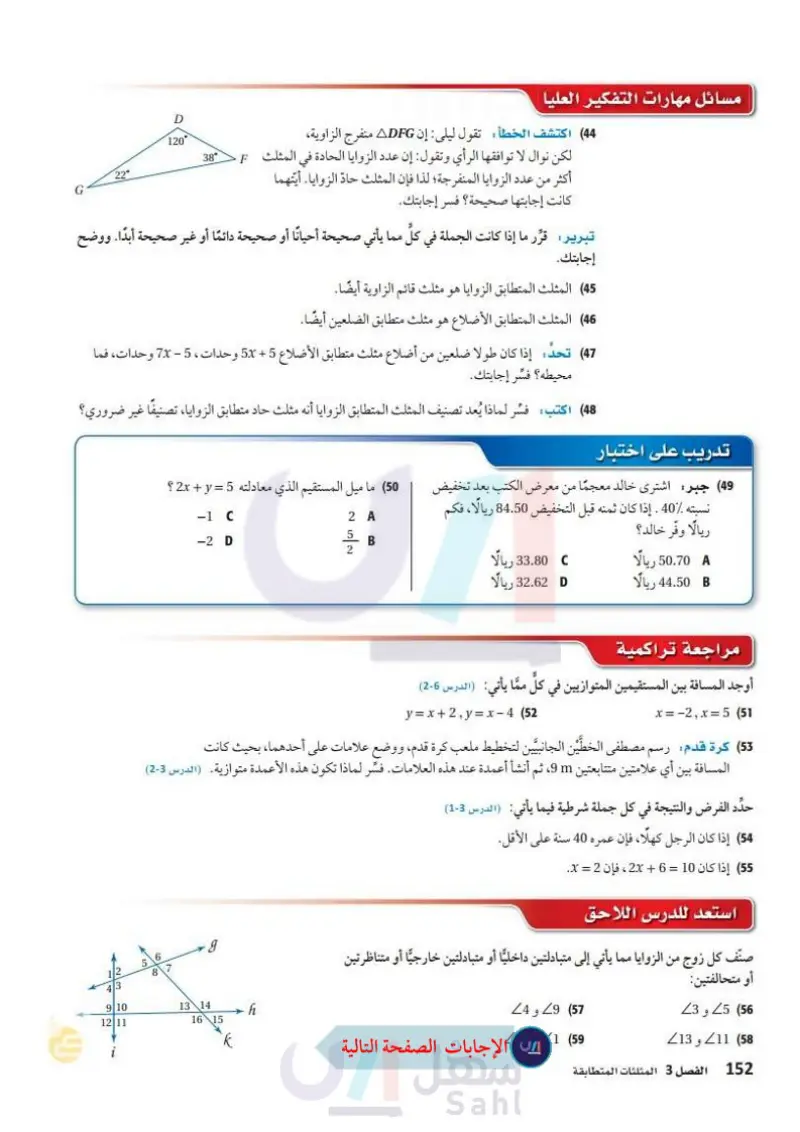
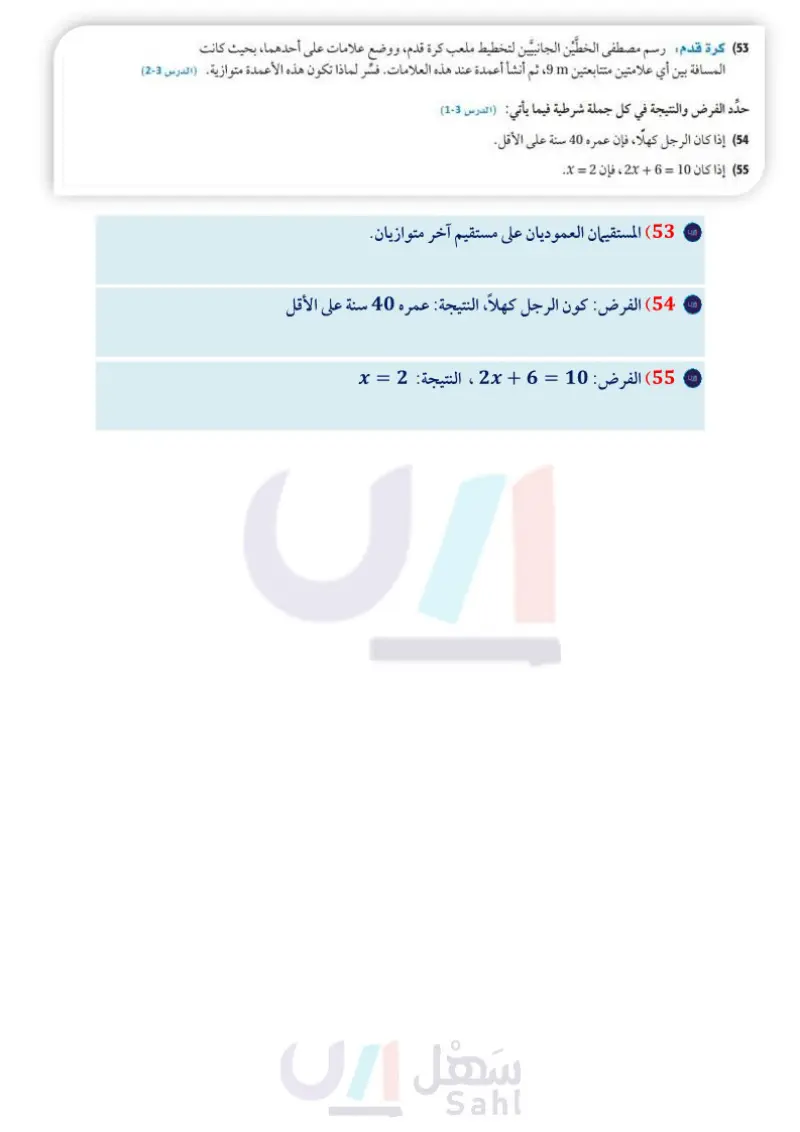
مسائل مهارات التفكير العليا F 38° (44) اكتشف الخطأ : تقول ليلى : إن ADFG منفرج الزاوية لكن نوال لا توافقها الرأي وتقول: إن عدد الزوايا الحادة في المثلث أكثر من عدد الزوايا المنفرجة؛ لذا فإن المثلث حاد الزوايا. أيتهما كانت إجابتها صحيحة ؟ فسر إجابتك. D 120° 22° G تبرير قرر ما إذا كانت الجملة في كل مما يأتي صحيحة أحيانًا أو صحيحة دائمًا أو غير صحيحة أبدًا. ووضح إجابتك. (45) المثلث المتطابق الزوايا هو مثلث قائم الزاوية أيضًا. (46) المثلث المتطابق الأضلاع هو مثلث متطابق الضلعين أيضًا. (47) تحد: إذا كان طولا ضلعين من أضلاع مثلث متطابق الأضلاع 5 + 5x وحدات ، 5 - 7x وحدات، فما محيطه؟ فسّر إجابتك. (48) اكتب فسر لماذا يعد تصنيف المثلث المتطابق الزوايا أنه مثلث حاد متطابق الزوايا، تصنيفا غير ضروري؟ تدريب على اختبار 49 جبر اشتری خالد معجمًا من معرض الكتب بعد تخفيض (50) ما ميل المستقيم الذي معادلته 5 = 2x + y ؟ نسبته 40 . إذا كان ثمنه قبل التخفيض 84.50 ريالا، فكم ريالًا وفّر خالد؟ 50.70 ريالا 33.80 ريالا 44.50 ريالا 32.62 ريالا مراجعة تراكمية 2 A B -1 C -2 D أوجد المسافة بين المستقيمين المتوازيين في كل مما يأتي: (مهارة سابقة) x= -2, x = 5 (51 y=x+2,y=x-4 (52 ا، بحيث كانت 53) كرة قدم : رسم مصطفى الخطَّين الجانبيين لتخطيط ملعب كرة قدم، ووضع علامات على أحدهما، بـ المسافة بين أي علامتين متتابعتين ، ثم أنشأ أعمدة عند هذه العلامات فسِّر لماذا تكون هذه الأعمدة متوازية. (مهارة سابقة) ، حدد الفرض والنتيجة في كل جملة شرطية فيما يأتي: (مهارة سابقة) (54) إذا كان الرجل كهلا، فإن عمره 40 سنة على الأقل. 55 إذا كان 10 = 6 + 2 ، فإن 2 = x . استعد للدرس اللاحق صنف كل زوج من الزوايا مما يأتي إلى متبادلتين داخليا أو متبادلتين خارجيًا أو متناظرتين أو متحالفتين Z3, Z5 (56 13, 211 (58 18 الفصل 3 المثلثات المتطابقة Z4,Z9 (57 (59) 1 و 11 10 12 11 56 8 7 13 14 .9 16 15 k ➤ h وزارة التعليم Ministry of Education 2024-1446

أيهما كانت إجابته صحيحة ؟ فسر اجابتك

كم ريالا وفر خالد؟

أوجد المسافة بين المستقيمين المتوازيين في كل مما يأتي

صنف كل زوج من الزوايا مما يأتي إلى متبادلتين داخليا أو متبادلتين خارجيا أو متناظرتين أو متحالفتين

قرر ما إذا كانت الجملة في كل مما يأتي صحيحة أحيانا أو صحيحة دائما أو غير صحيحة أبدا ووضح إجابتك

ما محيطه؟ فسر اجابتك

فسر لماذا يعد تصنيف المثلث المتطابق الزوايا انه مثلث حاد متطابق الزوايا، تصنيفا غير ضروري؟

ما ميل المستقيم الذي معادلته 2x+y=5 ؟

فسر لماذا تكون هذه الاعمدة متوازية؟

حدد الفرض والنتيجة في كل جملة شرطية فيما يأتي