المنصفات في المثلث - الرياضيات 1-1 - أول ثانوي
الفصل1: التبرير والبرهان
الفصل2: التوازي والتعامد
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
نشاط الفصل 1: التبرير والبرهان
نشاط الفصل 2: التوازي والتعامد
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
www.ien.edu.sa المنصفات في المثلث Bisectors of Triangle 4-1 فيما سبق درست منصف القطعة المستقيمة ومنصف الزاوية. والان الماذا؟ إن تصميم منطقة العمل على شكل مثلث كما في الصورة المجاورة يجعل إعداد الطعام أسرع؛ وذلك بتقليل عدد الخطوات التي تخطوها سيدة البيت. ولتعيين النقطة المتساوية البعد عن كل من الفرن ومصدر الماء والثلاجة، يمكنك استعمال أتعرف الأعمدة المنصفة في المثلثات وأستعملها. الأعمدة المنصفة لأضلاع المثلث. أتعرف منصفات الزوايا في المثلثات وأستعملها. المفردات: العمود المنصف perpendicular bisector المستقيمات المتلاقية مصدر انام الثلاجة الأعمدة المنصفة : تعلمت سابقا أن منصف قطعة مستقيمة هو أي قطعة أو مستقيم أو مستوى يقطع القطعة عند نقطة منتصفها، وإذا كان المنصف عمودياً على القطعة سُمِّي عمودًا منصفًا . A R B concurrent lines نقطة التلاقي point of concurrency مركز الدائرة الخارجية للمثلث circumcenter مركز الدائرة الداخلية للمثلث incenter PO منصف 3 AB RS عمود منصف لـ JK تذكر أن المحل الهندسي هو مجموعة من النقاط تحقق شرطًا معينا، فالعمود المنصف لقطعة مستقيمة هو المحل الهندسي لمجموعة نقاط في المستوى، تقع كلِّ منها على بعدين متساويين من طرفي القطعة المستقيمة، وهذا يقود إلى النظريتين الآتيتين: أضف إلى A + E D C D الأعمدة المنصفة نظريتان 4.1 نظرية العمود المنصف كل نقطة على العمود المنصف لقطعة مستقيمة تكون على بعدين متساويين من طرفي القطعة المستقيمة مثال: إذا كان CD عمودًا منصفا لـ AB ، فإن AC = BC . 4.2 عكس نظرية العمود المنصف كل نقطة على بعدين متساويين من طرفي قطعة مستقيمة تقع على العمود المنصف لتلك القطعة. مثال إذا كان AE = BE ، و CD هو العمود المنصف لـ AB فإن E تقع على CD . .B سوف تبرهن النظريتين 4.2 4.1 في السؤالين 2927 الدرس 1-4 - المنصفات في المثلث الت 81 Ministry of Edu 2024-1446

B 4.1 D 9 9 W Y 3 Z 2x +3 S R 4x 7 T إرشادات للدراسة المعلومة WX = ZX لوحدها لا تعد كافية لاستنتاج أن XY منصف ل WZ. Xi عمود مثال 1 استعمال نظريات العمود المنصف أوجد كل قياس مما يأتي : AB (a من المعطيات في الشكل المجاور ، نعلم أن CA عمود منصف لـ BD AB = AD AB = 4.1 WY (b نظرية العمود المنصف عوض WX=ZX,XY WZ معطيات عمود منصف لـ WZ عكس نظرية العمود المنصف W y WY = YZ تعريف منصف قطعة مستقيمة عوض نظرية العمود المنصف عوض اطرح 2x من الطرفين اجمع 7 إلى الطرفين اقسم الطرفين على 2 WY = 3 RT SR عمود منصف QT RT = RQ 4x - 7 = 2x + 3 2x-7=3 2x = 10 x=5 إرشادات للدراسة العمود المنصف إذن 13 = 7 - (5)4 = RT. تحقق من فهمك (14) إذا كان 25.3 = 22.42 = WX = 25.3, YZ ، فأوجد طول XY. (13) إذا كان 112 عمودًا منصفا لـ WZ = 14.9 ، XZ، فأوجد طول WX. IC إذا كان 11 عمودًا منصفا لـ WX = 4a - 15, WZ = a + 12 ، XZ فأوجد طول WX. عندما تتقاطع ثلاثة مستقيمات أو أكثر في نقطة مشتركة، فإن هذه المستقيمات تُسمى مستقيمات متلاقية. والنقطة التي تلتقي فيها المستقيمات تسمى نقطة التلاقي. ليس من الضروري أن وبما أن لكل مثلث ثلاثة أضلاع، فإنّ له ثلاثة أعمدة منصفة. وهذه الأعمدة يمر العمود المنصف المنصفة هي مستقيمات متلاقية. وتسمى نقطة تلاقي الأعمدة المنصفة لضلع مثلث برأس المثلث المقابل . فمثلا في AXYZ أدناه العمود المنصف ل XY لا يمر بالرأس Z. مركز الدائرة الخارجية للمثلث. نظرية 4.3 نظرية مركز الدائرة الخارجية للمثلث. التعبير اللفظي تلتقي الأعمدة المنصفة لأضلاع مثلث في نقطة تُسمى مركز الدائرة الخارجية للمثلث، وهي دائرة تمر برؤوس المثلث وهي على أبعاد متساوية من الرؤوس 141 X Z a W 6+ P c تتلاقى المستقيمات abc في النقطة P. A أضف إلى مطويتك D وزارة التعليم Ministry of Education 2024-1446 B F مثال : إذا كانت P مركز الدائرة الخارجية للمثلث AABC ، فإن PB = PA = PC الفصل 4 العلاقات في المثلث 82

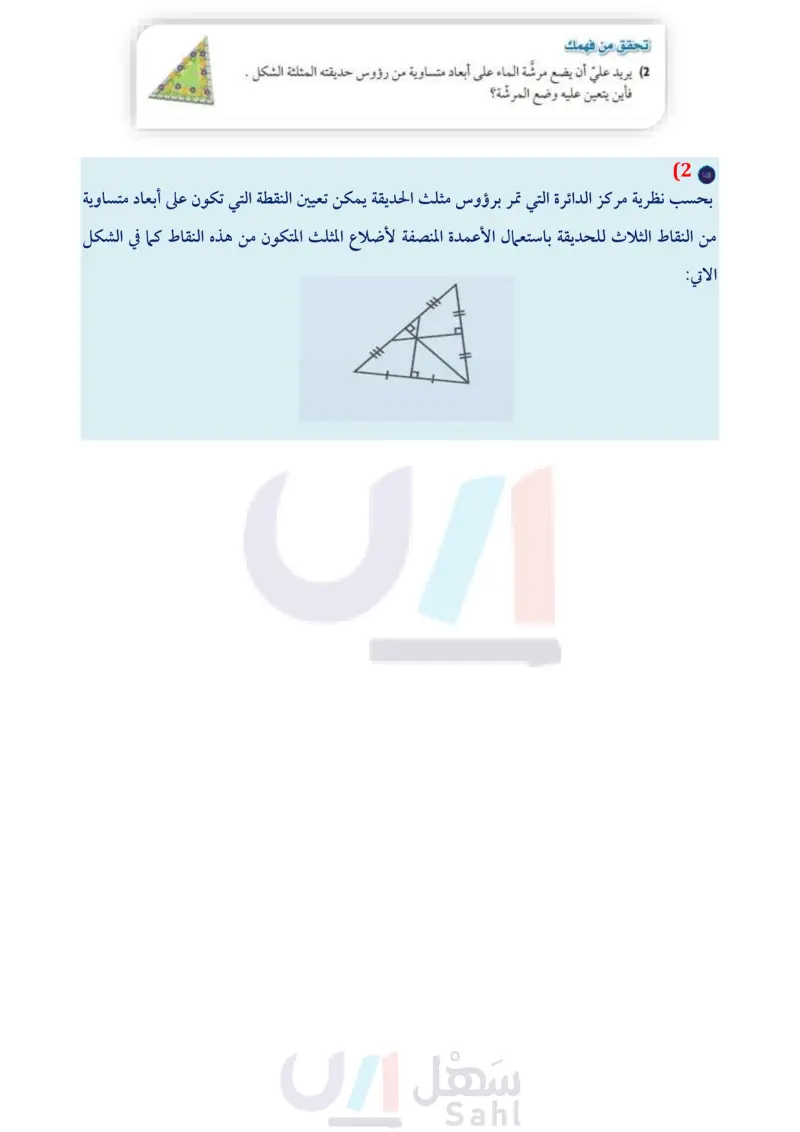
إرشادات للدراسة مركز الدائرة الخارجية للمثلث هو مركز الدائرة التي تمر برؤوس هذا المثلث برهان نظرية مركز الدائرة الخارجية للمثلث المعطيات: PD, PF, PE أعمدة منصفة للأضلاع AB, C, B على الترتيب. المطلوب : AP = CP = BP برهان حر A F C بما أن P تقع على العمود المنصف لـ AC، فإنها متساوية البعد عن . أي أن AP = CP . والعمود المنصف لـ BC يمر أيضًا بالنقطة .P . لذلك يكون CP = BP ، وتبعا لخاصية التعدي لعلاقة المساواة يكون AP = BP ؛ إذن AP = CP = BP. يمكن أن يقع مركز الدائرة الخارجية للمثلث داخل المثلث أو خارجه أو على أحد أضلاعه. P مثلث حاد الزوايا الربط مع الحياة يتركز معظم النشاط داخل المطبخ حول ثلاث مناطق عمل أساسية هي مصدر الماء، الثلاجة فرن الطبخ ويجب ألا يزيد مجموع أطوال مثلث قائم الزاوية مثلث منفرج الزاوية مثال 2 من واقع الحياة استعمال نظرية مركز الدائرة الخارجية للمثلث تصميم داخلي تطبيقًا للفكرة التي وردت في فقرة (لماذا؟)، إذا وضع فرن الطبخ ، ومصدر الماءK والثلاجة R في مطبخ كما في الشكل المجاور أوجد النقطة التي تكون على أبعاد متساوية من النقاط . بحسب نظرية مركز الدائرة الخارجية للمثلث، يمكن تعيين النقطة التي تكون على أبعاد متساوية من النقاط الثلاث باستعمال الأعمدة المنصفة لأضلاع المثلث المتكون من هذه النقاط. انسخ ASKR واستعمل المسطرة والمنقلة لرسم الأعمدة المنصفة لأضلاعه، فتكون النقطة C مركز الدائرة الخارجية للمثلث SKR . وهي النقطة المطلوبة. C Γ الأضلاع الثلاثة لمثلث منطقة العمل على سبعة أمتار. تحقق من فهمك 2) يريد علي أن يضع مرشّة الماء على أبعاد متساوية من رؤوس حديقته المثلثة الشكل . فأين يتعين عليه وضع المرشّة؟ منصفات الزوايا تعلم أ أنّ منصف الزاوية يقسمها إلى زاويتين متطابقتين كما يمكن أن يوصف منصف الزاوية بأنّه المحل الهندسي للنقاط الواقعة داخل الزاوية، وتكون على أبعاد متساوية من ضلعيها. ويقود هذا الوصف إلى النظريتين الآتيتين: B BD منصف لـ ABC الدرس 1-4 المنصفات في المثلث الت 83 Ministry of Edu 2024-1446

يتركز معظم النشاك داخل المطبخ حول ثلاث مناطق عمل اساسية هي : الماء، الثلاجة، فرن المطبخ
أضف إلى طويتك نظريتان 4.4 نظرية منصف الزاوية منصفات الزوايا كل نقطة تقع على منصف زاوية تكون على بعدين متساويين من ضلعيها. DA FD 1 BD, FE 1 BE B E DF B E 7 W X 41° Y 41° Z M 37 M 3x+57 J S'P A وزارة التعليم Ministry of Education 2024-1446 D مثال: إذا كان منصفا لـ DBE، وكان فإن DF = FE. 4.5 عكس نظرية منصف الزاوية كل نقطة تقع داخل الزاوية وتكون على بعدين متساويين من ضلعيها فإنها تكون واقعة على منصف الزاوية. مثال: إذا كان FD 1 BD, FE 1 BE F = FE ، فإن BF ينصف DBE ستبرهن النظريتين 4.5 ,4.4 في السؤالين 32,30 مثال 3 استعمال نظريتي منصفات الزاويا أوجد كل قياس مما يأتي : XY (a XY = XW XY = 7 mZJKL (b نظرية منصف الزاوية عوض إرشادات للدراسة. منصف الزاوية لا تعد المعلومة JL = LM في الفرع b لوحدها كافية لاستنتاج أن KL ينصف LJKM. بما أن KIM KM, L = LM ، فإن على بعدين متساويين من ضلعي LIKM. وبحسب عكس نظرية منصف الزاوية، فإن KL ينصف JKM ZJKL ZLKM mZJKL=mZLKM mZJKL = 37° SP (c SP=SM تعريف منصف الزاوية تعريف الزوايا المتطابقة عوض نظرية منصف الزاوية عوض اطرح 3x من الطرفين اجمع 7 إلى الطرفين اقسم الطرفين على 3 6x - 7 = 3 x +5 3x - 7 = 5 3x = 12 x= 4 إذن 17 = 7 - (4)6 = SP. تحقق من فهمك إذا كان 5 = mLBAC = 38, BC = 5, DC ، فأوجد mLDAC (3) إذا كان : 10 = mBAC = 40°, mLDAC = 40°, DC ، فأوجد BC (3) إذا كان AC ينصف DAB ، و 7 - BC = 4x + 8, DC = 9 x فأوجد BC الفصل 4 العلاقات في المثلث 84

منصف الزاوية
قراءة الرياضيات وكما هو الحال في الأعمدة المنصفة، بما أن للمثلث ثلاث زوايا، فإنّ له ثلاثة منصفات للزوايا تتلاقى في نقطة أضف إلى مطويتك 28° A F P D 15 12 F B 25 تُسمّى مركز الدائرة الداخلية للمثلث. مركز الدائرة الداخلية للمثلث نظرية 4.6 نظرية مركز الدائرة الداخلية للمثلث هو مركز الدائرة التي التعبير اللفظي: تتقاطع منصفات زوايا أي مثلث عند نقطة تُسمّى مركز تقطع (تتماس مع كل ضلع من أضلاع المثلث الدائرة الداخلية للمثلث، وهي على أبعاد متساوية من أضلاعه. في نقطة واحدة. ولهذا السبب فإن مركز هذه الدائرة يقع داخل المثلث دائما . مثال: إذا كانت P مركز الدائرة الداخلية للمثلث ABC ، فإن PD = PE = PF ستبرهن النظرية 4.6 في السؤال 28 مثال 4 استعمال نظرية مركز الدائرة الداخلية للمثلث أوجد كلا من القياسين الآتيين ، إذا كانت مركز الدائرة الداخلية لـ AABC . JF (a بما أن / على أبعاد متساوية من أضلاع AABC، بحسب نظرية مركز الدائرة الداخلية للمثلث، فإن JF = JE ؛ لذا أوجد JE باستعمال نظرية فيثاغورس نظرية فيثاغورس a2 + b2 = 2 عوض 122 144, 152 225 JE2 + 122 = 152 JE2 + 144 = 225 JE2 = 81 JE = ±9 اطرح 144 من الطرفين خذ الجذر التربيعي للطرفين وبما أن الطول لا يمكن أن يكون سالبا؛ إذن نأخذ الجذر التربيعي الموجب فقط. وبما أن JE = JF فإن 9 = JF mZJAC (b بما أن B ينصف CBE ، فإن MCBE = 2m JBE ؛ إذن 56 = (28)2 = mLCBE . وبالمثل ؛ MDCF = 2m DCJ ؛ إذن 50 = (25) 2 = mZDCF. 180° = LCBE + mZDCF + mLFAE نظرية مجموع قياسات زوايا المثلث mZCBE = 56°; mZDCF = 50 بسط. 56° + 50° + mZFAE = 180° 106° + mLFAE = 180° mZFAE = 740 اطرح 106 من الطرفين. وبما أن AJ ينصف LFAE، فإنّ 2mLJAC = mLFAE . وهذا يعني أن mLJAC = = mLFAE ، 30 24 P .mZJAC= إذن °37 = (74) 1 = تحقق من فهمك إذا كانت P مركز الدائرة الداخلية لـ AXYZ ، فأوجد القياسين الآتيين: الدرس 1-4 - المنصفات في المثلث الـ 85 Ministry of Edu 2024-1446 PK (4A ZLZP (4B

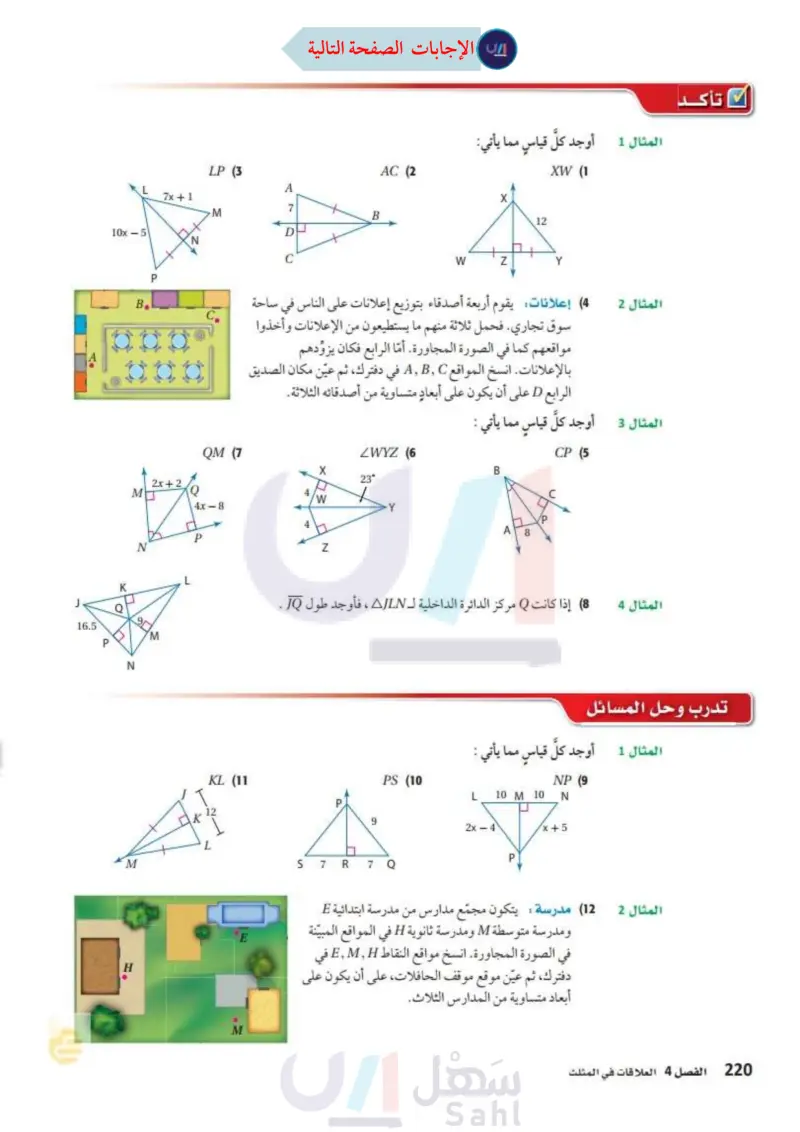
LP (3 L _7x + 1 7 M B 10x - 5 DH N K P B. MO C المثال 1 أوجد كل قياس مما يأتي: AC (2 X 12 XW (1 W Z Y المثال 2 (4) إعلانات يقوم أربعة أصدقاء بتوزيع إعلانات على الناس في ساحة سوق تجاري فحمل ثلاثة منهم ما يستطيعون من الإعلانات وأخذوا مواقعهم كما في الصورة المجاورة. أما الرابع فكان يزودهم بالإعلانات. انسخ المواقع في دفترك، ثم عين مكان الصديق الرابع D على أن يكون على أبعاد متساوية من أصدقائه الثلاثة. المثال 3 أوجد كل قياس مما يأتي : QM (7 ZWYZ (6 X 23° Q 4x-8 P N J 16.5 P O 9 وزارة التعليم Ministry of Education 2024-1446 M N M H KL (11 M 4 W Z Y B /p 8 CP (5 المثال 4 (8) إذا كانت Q مركز الدائرة الداخلية لـ AJLN ، فأوجد طول JQ. 9 تأكد تدرب وحل المسائل المثال 1 أوجد كل قياس مما يأتي : PS (10 L 10 M 10 ☐ NP (9 N 2x 4 x+5 S 7 R 7 Q المثال 2 (12) مدرسة : يتكون مجمّع مدارس من مدرسة ابتدائية E ومدرسة متوسطة M ومدرسة ثانوية H في المواقع المبينة في الصورة المجاورة. انسخ مواقع النقاط H, في دفترك، ثم عيّن موقع موقف الحافلات، على أن يكون على أبعاد متساوية من المدارس الثلاث. الفصل 4 العلاقات في المثلث 86

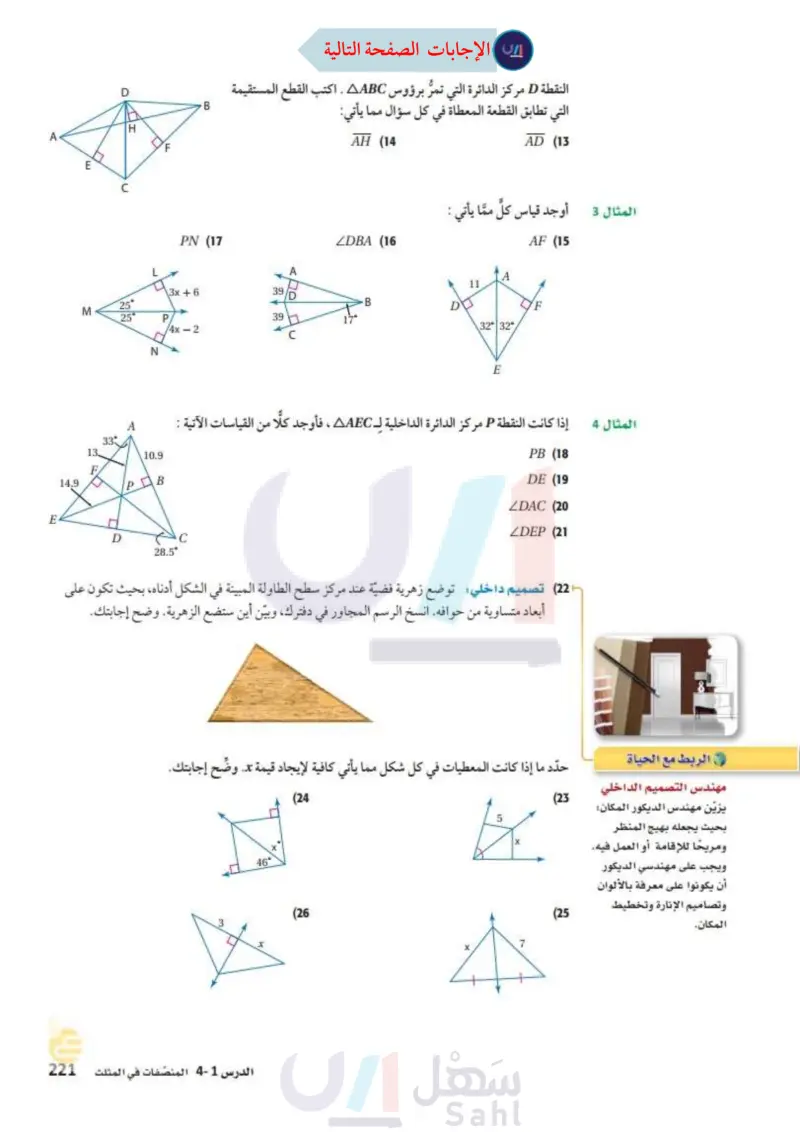
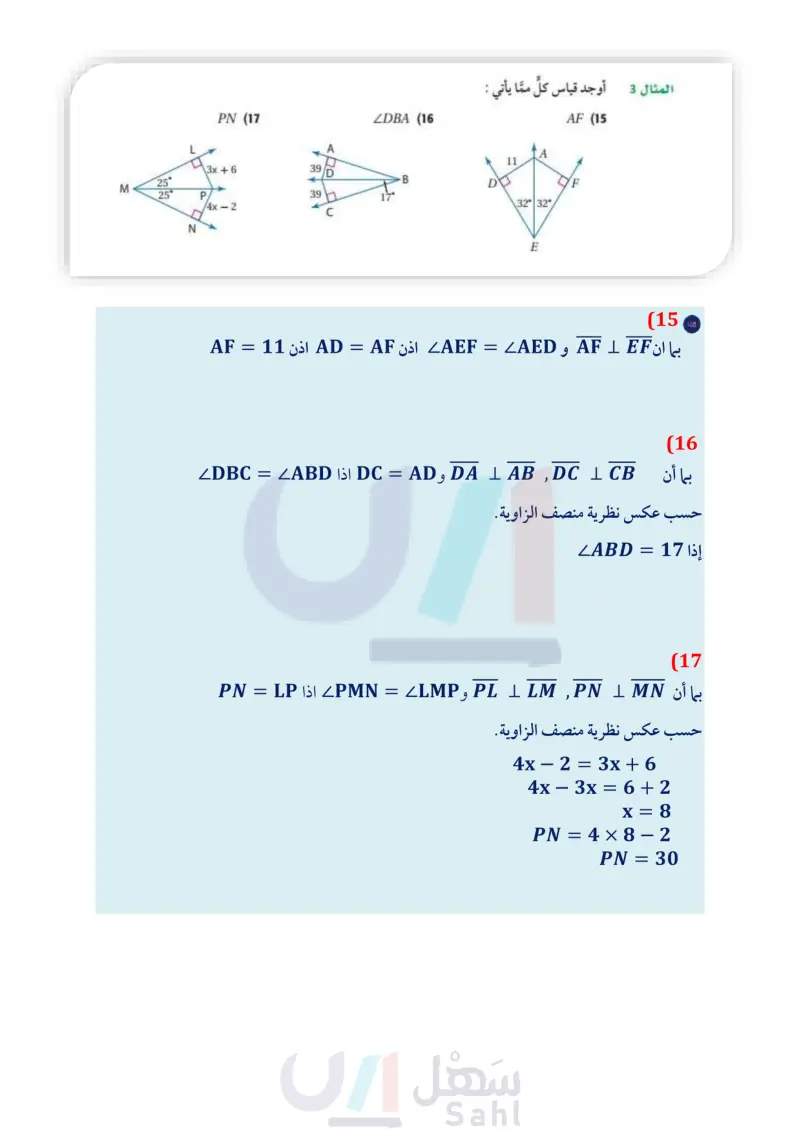
D A E C 14.9 H B PN (17 النقطة D مركز الدائرة التي تمرُّ برؤوس AABC . اكتب القطع المستقيمة التي تطابق القطعة المعطاة في كل سؤال مما يأتي: AH (14 DBA (16 AD (13 المثال 3 أوجد قياس كل مما يأتي : AF (15 A A 11 3x+6 39 /D 25° B M D F 25 P 396 4x-2 32° 32° N 33 13. 10.9 F PDB E المثال 4 إذا كانت النقطة P مركز الدائرة الداخلية لـ AAEC ، فأوجد كلا من القياسات الآتية : E D C 28.5° PB (18 DE (19 ZDAC (20 ZDEP (21 22) تصميم داخلي توضع زهرية فضية عند مركز سطح الطاولة المبينة في الشكل أدناه، بحيث تكون على أبعاد متساوية من حوافه. انسخ الرسم المجاور في دفترك ، وبين أين ستضع الزهرية. وضح إجابتك. Π الربط مع الحياة مهندس التصميم الداخلي يزين مهندس الديكور المكان بحيث يجعله بهيج المنظر ومريحا للإقامة أو العمل فيه. ويجب على مهندسي الديكور أن يكونوا على معرفة بالألوان وتصاميم الإنارة وتخطيط المكان. حدد ما إذا كانت المعطيات في كل شكل مما يأتي كافية لإيجاد قيمة تد. وضّح إجابتك. (23 (25 (24 46° (26 3 الدرس 1-4 المنصفات في المثلث الت - 87 Ministry of Education 2024-1446 7 X

مهندس التصميم الداخلي
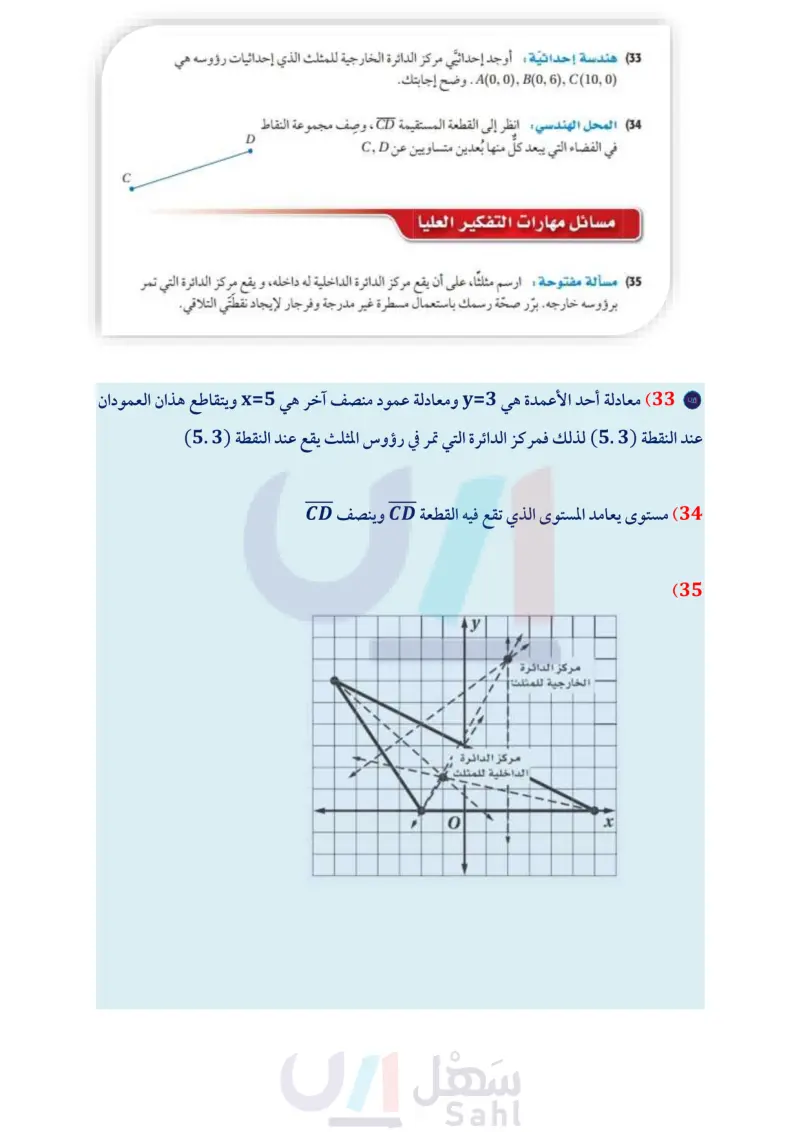
برهان اكتب برهانا ذا عمودين لكل من النظريتين الآتيتين: (27) النظرية 4.2 المعطيات CA = CB, AD = BD المطلوب : النقطتان تقعان على العمود المنصف لـ AB (28) النظرية 4.6 المعطيات AD, E, CF منصفات لزوايا AABC KP LAB, KQBC KR 1 AC المطلوب : KP = KQ = KR C P A R E K B QD (30) النظرية 4.5 E A B D مراجعة المفردات برهان اكتب برهانا حرا لكل من النظريتين الآتيتين: المحل الهندسي مجموعة من النقاط (29) النظرية 4.1 تحقق شرطا معينا. 31) اكتب بصيغة الميل والمقطع معادلة العمود المنصف للقطعة المستقيمة التي إحداثيا نقطتي طرفيها هما (43) (31). ووضح إجابتك. (32) برهان اكتب برهانا ذا عمودين للنظرية 4.4. (33) هندسة إحداثية: أوجد إحداثيَّي مركز الدائرة الخارجية للمثلث الذي إحداثيات رؤوسه هي (0 ,10)B(0, 6), C ,(0). وضح إجابتك . 34 المحل الهندسي: انظر إلى القطعة المستقيمة ،CD ، وصف مجموعة النقاط في الفضاء التي : يبعد كل منها بعدين متساويين عن CD D مسائل مهارات التفكير العليا (35) مسألة مفتوحة ارسم مثلثا على أن يقع مركز الدائرة الداخلية له داخله، و يقع مركز الدائرة التي تمر برؤوسه خارجه. برّر صحة رسمك باستعمال مسطرة غير مدرجة وفرجار لإيجاد نقطتي التلاقي. تبرير: حدد ما إذا كانت كل عبارة من العبارتين الآتيتين صحيحة دائمًا، أو صحيحة أحيانًا أو ليست صحيحة أبدًا. وبرّر إجابتك. (36) تتقاطع منصفات زوايا المثلث عند نقطة تكون على أبعاد متساوية من رؤوسه. (37 في المثلث المتطابق الضلعين، يكون العمود المنصف للقاعدة منصّفًا لزاوية الرأس المقابلة للقاعدة. 38 اكتب قارن بين الأعمدة المنصفة لأضلاع المثلث ومنصفات زواياه مبينا أوجه الشبه وأوجه الاختلاف. وزارة التعليم Ministry of Education 2024-1446 وقارن بين نقطتي التلاقي. الفصل 4 العلاقات في المثلث 88

حدد ما إذا كانت كل عبارة من العبارتين الآتيتين صحيحة دائما أو صحيحة احيانا أو ليست صحيحة أبدا وبرر إجابتك

قارن بين الأعمدة المنصفة لأضلاع المثلث ومنصفات زواياه مبينا أوجه الشبه وأوجه الاختلاف وقارن بين نقطتي التلاقي

المحل الهندسي مجموعة من النقاط تحقق شرطا معينا
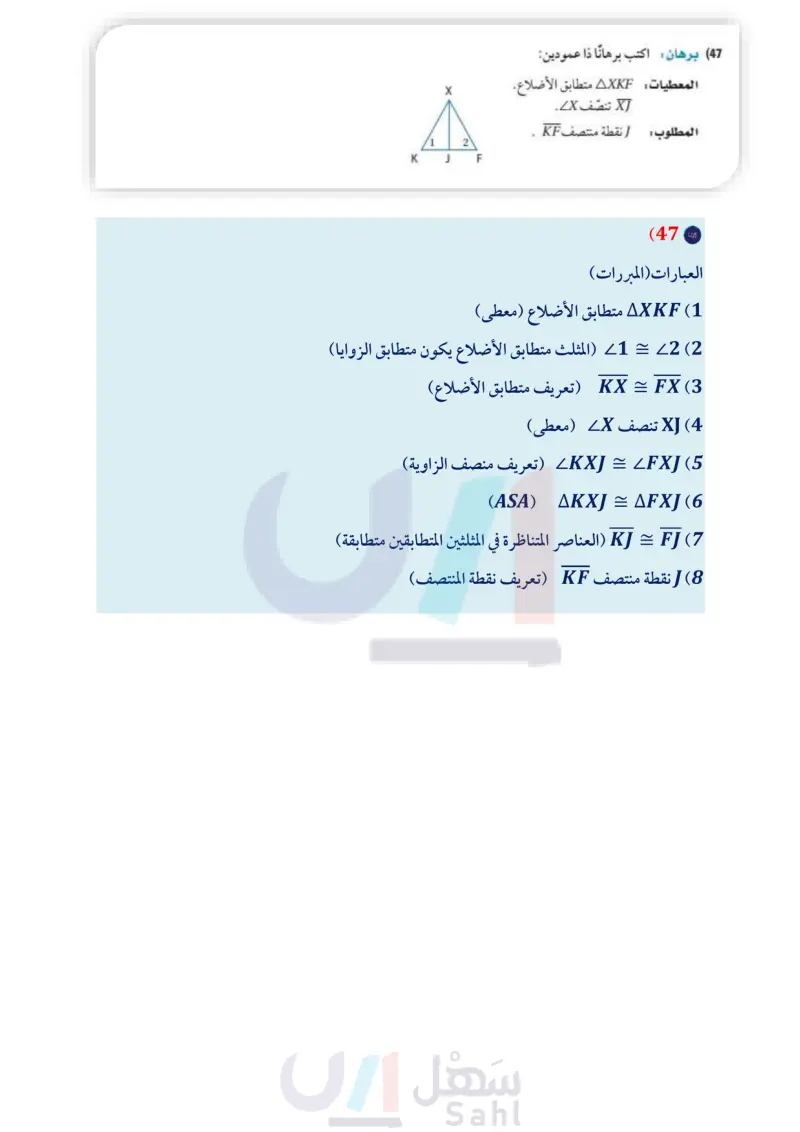
تدريب على اختبار 39) بأي نقطتين يمر العمود المنصف للضلع IL في AJKL؟ 3x+9 x+3 يساوي: (40) إذا كانت 3 x ، فإن ! | (?, c S(?, ?) OT(2b, 0) الدرس 1-4 - المنصفات في المثلث الت89 Ministry of Ex 2024-1446 x+9 A x + 3 B x C Q 3D (43 УА B(0, a) K R J, R C T.K A S, K D L, Q B مراجعة تراكمية عين الإحداثي المجهول في كل من المثلثات الآتية : ( الدرس 7-3) OA(0,0) C(?, ?) (42 L(?, b) y OJ(0, 0) K(6a, 0) (41 أوجد البعد بين المستقيم والنقطة المعطاة في كل مما يأتي : (مهارة سابقة) K J F y=5, (-2, 4) (44 y=2x+2, (-1,-5) (45 2x-3y=-9, (2, 0) (46 استعد للدرس اللاحق (47) برهان اكتب برهانا ذا عمودين: المعطيات AXKF متطابق الأضلاع XJ تنصف X. ا نقطة منتصف KF . المطلوب :