خصائص اللوغاريتمات - رياضيات1-3 - ثالث ثانوي

2-4 خصائص اللوغاريتمات Properties of Logarithms رابط الدرس الرقمي www.ien.edu.sa فيما سبق درستُ إيجاد قيم عبارات لماذا؟ لوغاريتمية . (الدرس (3-2) يُعد الاحتفاظ بمستوى معين من الحموضة في الأطعمة أمرًا مهما لبعض الأشخاص الذين يعانون حساسية في المعدة. إذ تحتوي بعض الأطعمة على أحماض أكثر مما تحتوي عليه من القواعد. ويستعمل تدريج pH لقياس درجة الحموضة أو القاعدية، فانخفاضه يدل على حمضية الوسط، وارتفاعه يدل على قاعديته. ويُعد هذا المقياس مثالًا والآن : أطبق خاصية المساواة للدوال اللوغاريتمية آخر على المقاييس اللوغاريتمية التي تعتمد على قوة العدد 10. فقيمة pH أبسط عبارات وأجد قيمها للقهوة تساوي 5 بينما تساوي 7 للماء النقي؛ لذا فإن تركيز أيون القهوة الهيدروجيني ( يعادل 100 مرة تركيزه في الماء النقي. باستعمال خصائص اللوغاريتمات. لأن [+] 10810 = pH، فإنه يمكنك كتابة المعادلة الآتية: المادة مستوى pH عصير الليمون المخلل الطماطم القهوة الحليب قهوة الماء النقي البيض 2.1 3.5 4.2 5.0 6.4 7.0 7.8 للقهوة + log 10 [H+] للماء النقي = 10810 = == – log10 [H+] pH. للقهوة pH - للماء النقي pH والتي تكتب بالشكل : للقهوة PH - للماء النقي pH، وذلك باستعمال خاصية القسمة في اللوغاريتمات التي للقهوة (H) ة(+H) للماء النقي (+H) ستتعلمها في هذا الدرس. وبتحويل هذه الصيغة اللوغاريتمية إلى الصيغة الأسية، ثم التعويض، تجد أن: = 107-5102 100 = للقهوة (+H) للماء النقي (+H) خصائص اللوغاريتمات تتحقق خاصية المساواة في الدوال اللوغاريتمية كما هو الحال في الدوال الأسية. مفهوم أساسي خاصية المساواة في الدوال اللوغاريتمية التعبير اللفظي : إذا كان 6 عددًا موجبًا حيث 1 ، فإن 10gx = 10g إذا وفقط إذا كان x = y. مثال : إذا كان 10858 = logsx، فإن 8 = x ، وإذا كان 8 = x فإن 10858 = logsx وبما أن اللوغاريتمات ترتبط بالأسس ، فيمكنك اشتقاق خصائصها من خصائص الأسس ، ويمكنك اشتقاق خاصية الضرب في اللوغاريتمات من خاصية الضرب في الأسس. مفهوم أساسي خاصية الضرب في اللوغاريتمات التعبير اللفظي: لوغاريتم حاصل الضرب هو مجموع لوغاريتمات عوامله. الرموز إذا كانت x, y, b أعدادًا حقيقية ،موجبة، حيث 1 # b فإن: مثال : .log₁ xy = log₁ x + log₁ y log₂ [(5)(6)] = log2 5 + log2 6 6 لإثبات صحة هذه الخاصية افترض أن b = x و b = y ، وباستعمال تعريف اللوغاريتمات، فإن m = logb x, n = logy . bmbn = xy = xy bm + n log₁ bm + n = log₁ xy : m+n=log, xy logy x + logb y = log xy عوض خاصية ضرب القوى خاصية المساواة للدوال اللوغاريتمية الخصائص الأساسية للوغاريتمات n عوض عن , بالقيمتين 18 10gx على الترن ' يمكنك استعمال خاصية الضرب في اللوغاريتمات لتقريب قيم عبارات لوغاريتمية. وزارة التعليم الدرس 4-2- خصائص اللوغاريتمات M103 Ed 2024-1446

104 مثال 1 استعمال خاصية الضرب في اللوغاريتمات استعمل 30.7925 108 لتقريب قيمة 108192 . 192 = 64 × 3 = 4³× 3 log4 192 = log4 (4³ × 3) خاصية الضرب في اللوغاريتمات الخصائص الأساسية للوغاريتمات = = 1084 43 + 1084 3 = 3 + log4 3 log4 3≈ 0.7925 ≈3+0.7925 ≈ 3.7925 تحقق من فهمك 1) استعمل 0.5 = 10842 لإيجاد قيمة 108432. تذكّر أن قسمة القوى ذات الأساس نفسه تكون بطرح الأسس وخاصية القسمة في اللوغاريتمات شبيهة بها. . افترض أن bm = x, b = y ، إذن logb x = m, logb y = n bm = bn bm - n n = x y X log b bm ― = log b X m ― n = log b y x log₁ x = log y = log b y خاصية قسمة القوى خاصية المساواة للدوال اللوغاريتمية الخصائص الأساسية للوغاريتمات عوض عن , m بالقيمتين 10 10gb x على الترتيب خاصية القسمة في اللوغاريتمات مفهوم أساسي التعبير اللفظي : لوغاريتم ناتج القسمة يساوي لوغاريتم المقسوم مطروحًا منه لوغاريتم المقسوم عليه. الرموز إذا كانت x y b أعدادًا حقيقية موجبة، حيث 1 6 فإن : مثال: x - log₁₁ = log₁ x = log y 1082 5 6 = = log₂ 5 — log2 6 - مثال 2 استعمال خاصية القسمة في اللوغاريتمات استعمل 0.8982 ~ 5 108، لتقريب قيمة 7.2 1086. 72 = 36 = 6² log6 7.2 = 7.2 = 10 5 5 log6 1086 (3) خاصية القسمة في اللوغاريتمات الخصائص الأساسية للوغاريتمات = 1086 62 - 1086 5 = = 2 - 0.8982 108 5 ~ 0.8982 = 1.1018 تحقق من فهمك (2) استعمل 108320.63 لتقريب قيمة 4.5 1083. الفصل 2 العلاقات والدوال الأسية واللوغاريتمية وزارة التعليم Ministry of Education 2024-1446

الربط مع الحياة المطر الحمضي أكثر حمضية من المطر الطبيعي، حيث يتكون من اختلاط الدخان، وأبخرة المشتقات النفطية وغيرها برطوبة الجو. والمطر الحمضي مسؤول عن التعرية، كما يظهر في الصورة أعلاه. مثال 3 من واقع الحياة استعمال خاصية القسمة في اللوغاريتمات 1 [H+] :علوم : يُعطى الأس الهيدروجيني للمحلول pH بالعلاقة: 10810 = pH حيث [+H] يمثل تركيز أيون الهيدروجين بوحدة مول لكل لتر أوجد تركيز أيون الهيدروجين في لتر من المطر الحمضي قيمة pH له 4.2. افهم : أُعطى في المسألة صيغة إيجاد pH، وقيمة pH للمطر الحمضي. والمطلوب معرفة تركيز أيون الهيدروجين في لتر من المطر الحمضي. خطط اكتب المعادلة وحلها لإيجاد [H] . حل تحقق المعادلة الأصلية pH = log10 [H+] pH = 4.2 4.2 = log10 [H+] خاصية القسمة في اللوغاريتمات 4.2 = log 10 1 log10 [H+] – log10 1=0 4.2 = 0 - 10810 [+] بسط 4.2 = -log10 [H+] اضرب كلا الطرفين في 1 تعريف اللوغاريتم -4.2 = log10 [H+] 10–4.2 = [H+] إذن يوجد 4.2-10 أو 0.000063 مول من الهيدروجين تقريبًا في اللتر الواحد من المطر الحمضي. 1 4.2 = log10 [H+] 1 4.2 = 10810 1 10-4.2 4.2 = 108101 - 10810104.2 4.20 - (−4.2) تحقق من فهمك 4.2 = 4.2 ✓ pH = 4.2 عوض 4.2-10 = [H] خاصية القسمة في اللوغاريتمات الخصائص الأساسية للوغاريتمات 3) استعمل الجدول الوارد في فقرة "لماذا؟" وأوجد تركيز أيون الهيدروجين في عصير الليمون . تذكر أن قوة القوة توجد بضرب ،الأسس ، وخاصية لوغاريتم القوة شبيهة بها. مفهوم أساسي خاصية لوغاريتم القوة التعبير اللفظي : لوغاريتم القوة يساوي حاصل ضرب الأس في لوغاريتم أساسها. الرموز لأي عدد حقيقي m، وأي عددين موجبين xb ، حيث 1 b، فإن مثال : m logb x = m log x 10g2 65 = 5 10g2 6 ستبرهن خاصية لوغاريتم القوة في السؤال 48 وزارة التعليم تعليم الدرس 4-2 خصائص اللوغاريتمات M105 Ed 2024-1446

إرشادات للدراسة التحقق من الإجابة يمكنك التحقق من إجابة مثال 4 بإيجاد قيمة 4.6438 24 مستعملا الحاسبة والإجابة التي ستحصل عليها هي 25 تقريبًا، ولكون log2 25 4.6438 4.6438 .2 فهذا يعني أن 25 ~ 106 مثال 4 استعمال خاصية لوغاريتم القوة إذا كان 2.3219 5 1082 ، فقرّب قيمة 25 1082 5² = 25 log2 25 = log2 52 خاصية لوغاريتم القوة = 2 log₂ 5 log 25 = 2.3219 ≈2(2.3219) 4.6438 1 تحقق من فهمك (4) إذا كان 108371.7712 ، فقرّب قيمة 49 1083. يمكنك استعمال خصائص اللوغاريتمات لتبسيط العبارات اللوغاريتمية. مثال 5 تبسيط العبارات اللوغاريتمية دون استعمال الآلة الحاسبة، احسب قيمة 108464 . بما أن أساس اللوغاريتم 4 عبّر عن 64 على صورة قوة 4 . 5/64 = 645 log4√√64 = log4 645 43 = 64 = 1084 (43) = log4 3 45 3 = log44 خاصية قوة القوة خاصية لوغاريتم القوة log b = 1 = 3 (1) - = 5 تحقق من فهمك log√36 (5A log 7 √49 (5B يمكنك استعمال خصائص اللوغاريتمات لإعادة كتابة العبارات اللوغاريتمية من الصورة المختصرة إلى الصورة المطولة، إذ يمكنك تحويل الضرب إلى جمع، والقسمة إلى طرح، والقوى والجذور إلى ضرب. الفصل 2 العلاقات والدوال الأسية واللوغاريتمية وزارة التعليم Ministry of Education 2024-1446

مثال 6 كتابة العبارات اللوغاريتمية بالصورة المطولة اكتب كل عبارة لوغاريتمية فيما يأتي بالصورة المطولة: log 1082 12x5y-2 (a العبارة المعطاة هى لوغاريتم حاصل ضرب 1,125,22 خاصية الضرب في اللوغاريتمات خاصية لوغاريتم القوة خاصية الضرب في اللوغاريتمات خاصية لوغاريتم القوة خاصية القسمة في اللوغاريتمات 1 √3-2x=(3-2x)5 log2 12x5y-² = log2 12 + log2x5 + log2 y¯ - = log2 12 + 5 log2 x - 2 log2 y log 2 a2b-3 c-2 (b log 2 a² b −³ c −² = log 2 a² + log 2 b−3 + log 2 c −2 = 2 log2 a 3 log2b - 2 log 2 c log 3 1083 x-1 √3-2x (c x-1 √√3-2x = log 3 (x-1) - log 3 √3 - 2x = log 3 (x − 1) — log 3 (3 — 2x) 5/5 - - = 1083 (x - 1) - - 1083 (3 - 2x ) ― 10g 4 3/1-x 2x + 1 (6 log 65x3y7z0.5 (6B تحقق من فهمك 10813 6a3bc4 (6A ويمكنك استعمال خصائص اللوغاريتمات السابقة في إعادة كتابة العبارات اللوغاريتمية من الصورة المطولة إلى خاصية لوغاريتم القوة 1 (x + 6) 3 = x + 6 خاصية القسمة في اللوغاريتمات بإنطاق المقام تنبيه لوغاريتم المجموع لو غاريتم المجموع أو الفرق لا يساوي مجموع أو فرق اللوغاريتمات. الصورة المختصرة. مثال 7 كتابة العبارات اللوغاريتمية بالصورة المختصرة اكتب كل عبارة لوغاريتمية فيما يأتي بالصورة المختصرة: 4 log3 x - 1 ½ log3 (x + 6) (a - 3 1083 4 log3 x − 1½-½ log3 (x + 6) = log3 x4 – log3 (x + 6)³ - = 1083 x4 - 1083 x + 6 x4 = 1083 = log3 x + 6 (x+6)² x + 6 0.5 log 7 (x + 2) + 6 log72x (b 6(x + 2 + 610g7 2x = log ( x + 20.5 + log 7 (2x ) 0.51087 خاصية لوغاريتم القوة (x+2) 0.5= √√√x+2,26 = 64 خاصية الضرب في اللوغاريتمات • log 3 (2x-1)-log 3 (x + 1) (7B وزارة التعليم الدرس 4-2 خصائص اللوغاريتمات Mi107 Ed 2024-1446 = log 7 √√x + 2 + log764x6 = log7 64x6 Vx + 2 تحقق من فهمك -5 log2 (x + 1) + 3 log2 (6x) (7A loga (x+4) loga x + loga 4.

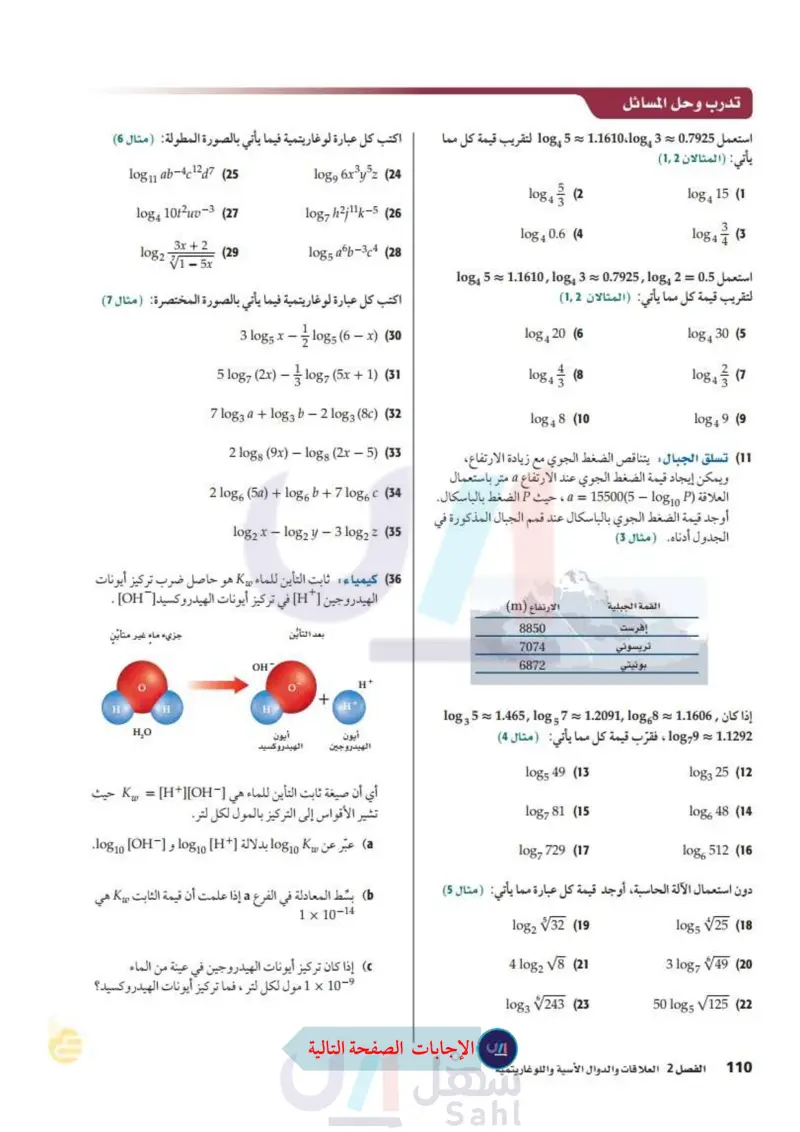
تدرب وحل المسائل اكتب كل عبارة لوغاريتمية فيما يأتي بالصورة المطولة : ( مثال (6) استعمل 0.7925 ~ 3 log،1.1610 ~ 5 108 لتقريب قيمة كل مما يأتي: المثالان (12) log11 ab-4c12d7 (25) log4 10t²uv-3 (27 log, 6x³y5z (24 log7h2j11k-5 (26 log2 3x + 2 V1 – 5x (29 log5 a6b-3c4 (28 5 log4 3 (2 log 4 0.6 (4 log4 15 (1 log4 4 (3 ' استعمل 0.5 = 10842 0.7925 ~ 3 log4 5 ~ 1.1610 ,log4 لتقريب قيمة كل مما يأتي: (المثالان (12) اكتب كل عبارة لوغاريتمية فيما يأتي بالصورة المختصرة: (مثال (7) 3 log5 x 1½ log5 (6 - x) (30 - 5 log7 (2x) - 1 ½ log7 (5x + 1) (31 7 log3 a + log3 b - 210g3 (8) (32 2 logg (9x) — logg (2x — 5) (33 2 log 6 (5a) + log6 b + 7 log6 c (34 log2 x - log2 y — 3 log2 z (35 (36 كيمياء ثابت التأين للماء Ko هو حاصل ضرب تركيز أيونات الهيدروجين [H] في تركيز أيونات الهيدروكسيد[ OH] . جزيء ماء غير متأين OH بعد التأين H + H H H Но + H+ أيون الهيدروجين أيون الهيدروكسيد log420 (6 log4 30 (5 log4 (8 log4 1387) (7 log48 (10 log49 (9 (11) تسلق الجبال : يتناقص الضغط الجوي مع زيادة الارتفاع ويمكن إيجاد قيمة الضغط الجوي عند الارتفاع a متر باستعمال العلاقة ) 1010 - (5)15500 = a ، حيث P الضغط بالباسكال. أوجد قيمة الضغط الجوي بالباسكال عند قمم الجبال المذكورة في الجدول أدناه (مثال (3) القمة الجبلية الارتفاع (m) إفرست تريسوني بونيتي 8850 7074 6872 إذا كان, 1.1606 ~ 1.2091,10g68 × 7 5 108 ,1.465 ~ 5 1083 1.1292 10g79، فقرّب قيمة كل مما يأتي: (مثال (4) log5 49 (13 log3 25 (12 log781 (15 log 48 (14 log7 729 (17 logo 512 (16 دون استعمال الآلة الحاسبة، أوجد قيمة كل عبارة مما يأتي: (مثال (5) أي أن صيغة ثابت التأين للماء هي [-K = [H+][OH حيث تشير الأقواس إلى التركيز بالمول لكل لتر. .log10 [OH-], log10 [H+] ¿Y log 10 Kw a عبّر عن Kw بسط المعادلة في الفرع a إذا علمت أن قيمة الثابت Kw هي وزارة التعليم Ministry of Education 2024-1446 1 × 10-14 إذا كان تركيز أيونات الهيدروجين في عينة من الماء 10-9 × 1 مول لكل لتر ، فما تركيز أيونات الهيدروكسيد؟ log2 √32 (19 log5 √25 (18 4 log2 √8 (21 3 log7 √49 (20 log3 √243 (23 50 log5 125 (22 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 108

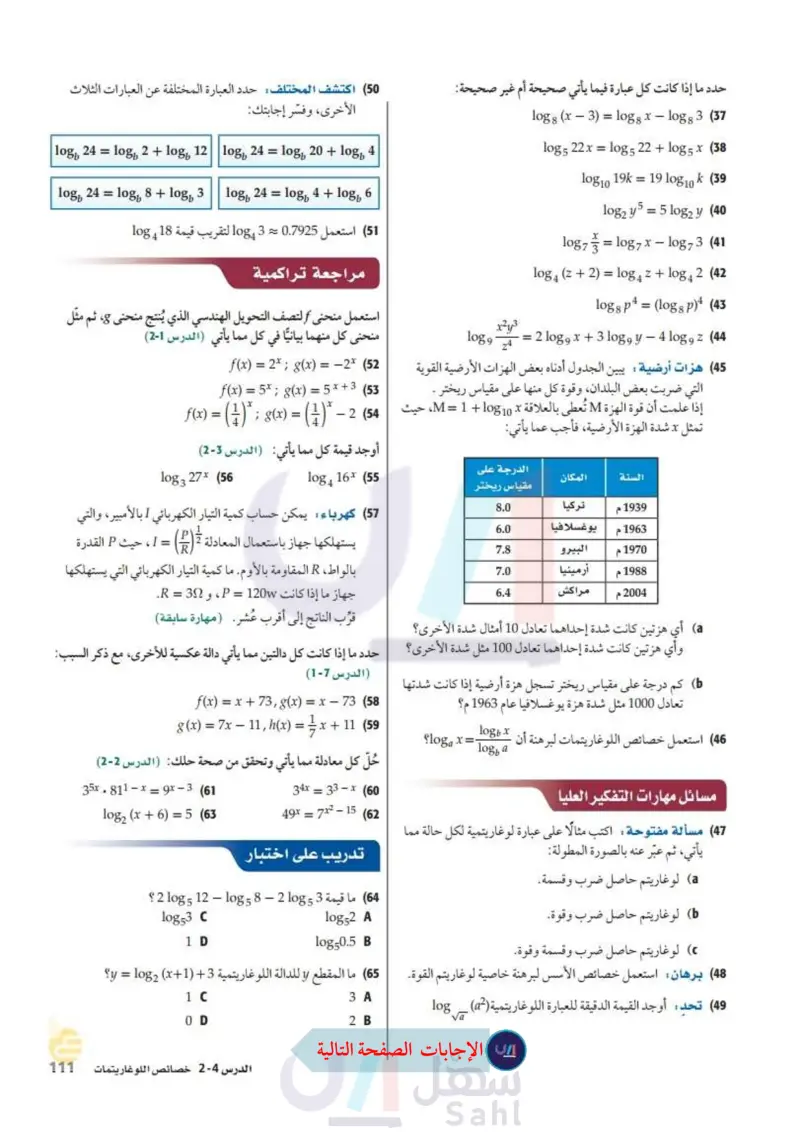
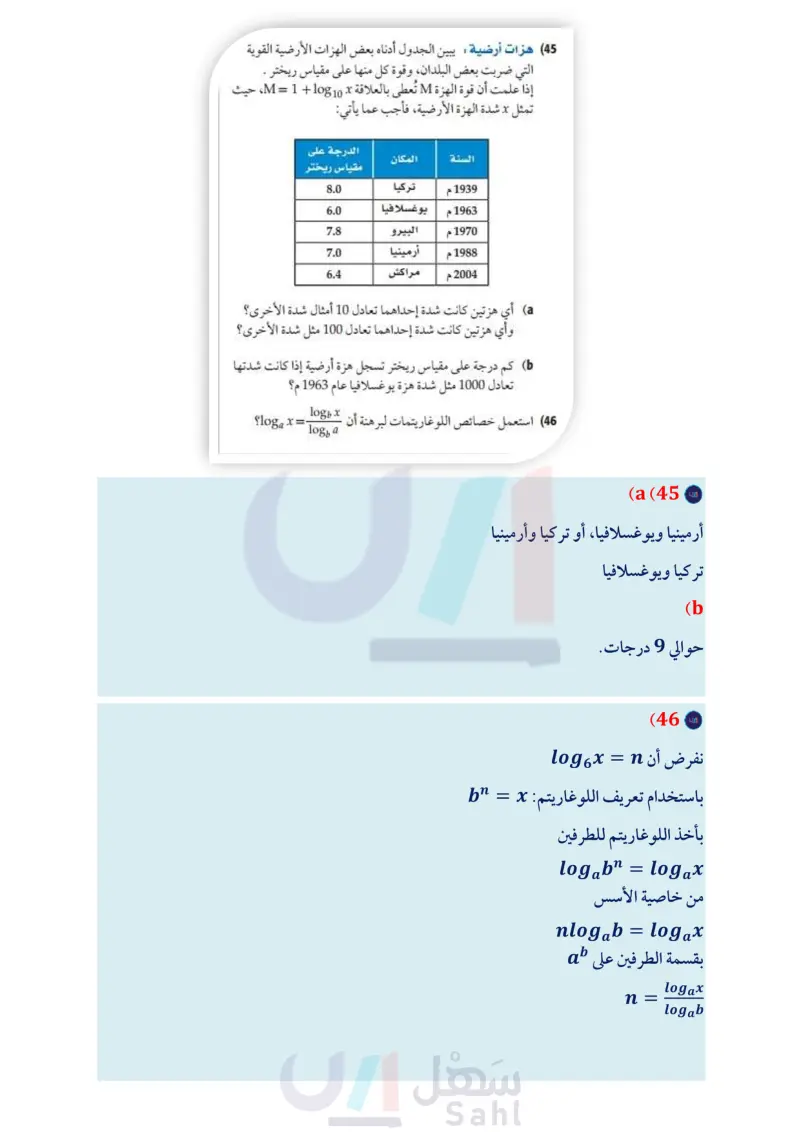
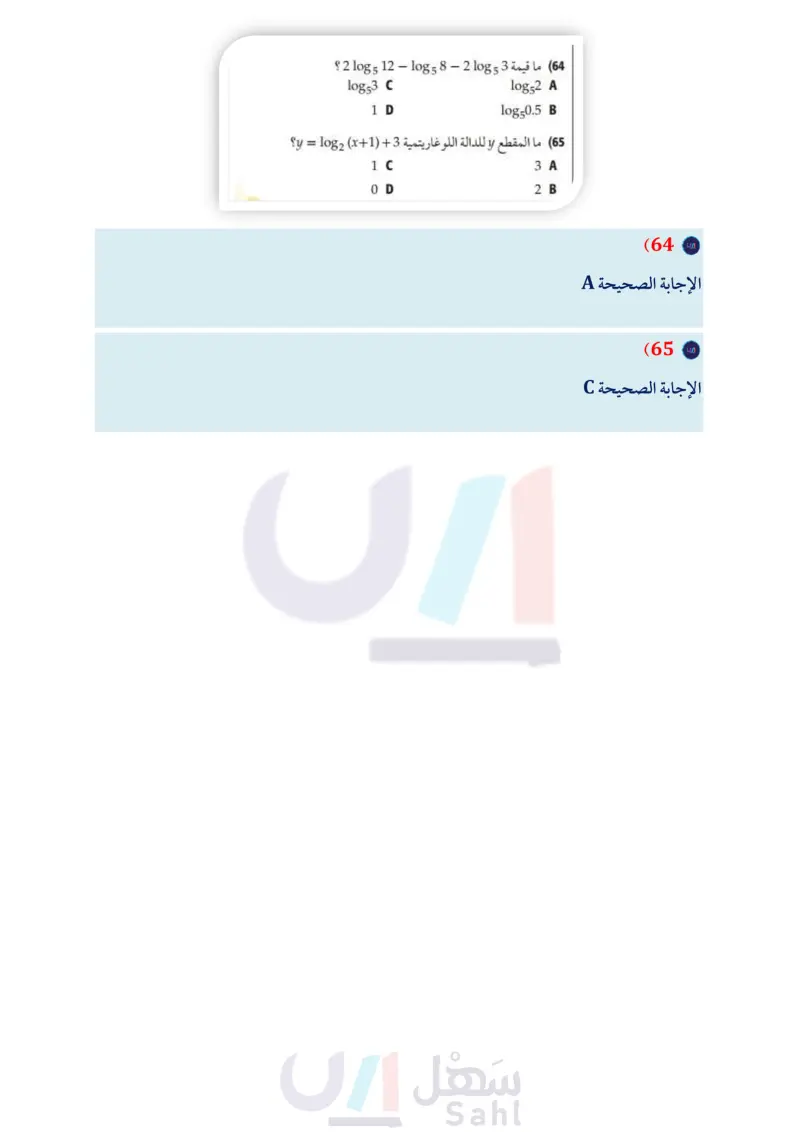
حدد ما إذا كانت كل عبارة فيما يأتي صحيحة أم غير صحيحة: logg (x-3)= log 8 x - logg 3 (37 g 1085 22x = 10g522 + 10g5 x 38 log10 19k = 19 log10k (39 log2 y5 = 5 log2 y (40 1=log7x-log73 (41 10873 log 4 (z + 2) = log 4 z + log 42 (42 logs p4 = (logsp)4 (43) x23 log9 z4 = 2 log, x + 3 log, y - 4 log, z (44 (45 هزات أرضية : يبين الجدول أدناه بعض الهزات الأرضية القوية التي ضربت بعض البلدان، وقوة كل منها على مقياس ريختر إذا علمت أن قوة الهزة تُعطى بالعلاقة : 10810 + 1 = M، حيث M x تمثل x شدة الهزة الأرضية، فأجب عما يأتي: (50) اكتشف المختلف: حدد العبارة المختلفة عن العبارات الثلاث الأخرى، وفسّر إجابتك: 108 24 = 1080 2 + 1080 12 108 24 = 10g 20 + 10gb 4 log 24 = log 8 + 10gb 3 log 24 = log 4 + log₁ 6 (51) استعمل 0.7925 10843 لتقريب قيمة 108418 مراجعة تراكمية استعمل منحنى التصف التحويل الهندسي الذي يُنتج منحنى 8، ثم مثل منحنى كل منهما بيانيا في كل مما يأتي (الدرس 1-2) f(x) = 2x ; g(x) = -2x (52 f(x) = 5* ; g(x) =5x+3 (53 ƒ(x) = (1-1)* ; 8(x) = ( 1 )* −2 (54 1939 1963 الدرجة على السنة المكان مقياس ريختر تركيا م 1م يوغسلافيا 1970 م البيرو 1988 م أرمينيا 2004 م مراکش 8.0 6.0 7.8 7.0 6.4 a أي هزتين كانت شدة إحداهما تعادل 10 أمثال شدة الأخرى؟ أوجد قيمة كل مما يأتي: (الدرس (3-2) log4 16x (55 log 3 27% (56 (57) كهرباء يمكن حساب كمية التيار الكهربائي I بالأمبير، والتي يستهلكها جهاز باستعمال المعادلة (R) = I ، حيث P القدرة بالواط، R المقاومة بالأوم. ما كمية التيار الكهربائي التي يستهلكها جهاز ما إذا كانت P = 120w ، و 3 = R. قرب الناتج إلى أقرب عُشر. (مهارة سابقة) وأي هزتين كانت شدة إحداهما تعادل 100 مثل شدة الأخرى؟ حدد ما إذا كانت كل دالتين مما يأتي دالة عكسية للأخرى، مع ذكر السبب: الدرس (17) ) كم درجة على مقياس ريختر تسجل هزة أرضية إذا كانت شدتها تعادل 1000 مثل شدة هزة يوغسلافيا عام 1963م؟ f(x) = x+73, g(x) = x - 73 (58 1 (46) استعمل خصائص اللوغاريتمات لبرهنة أن مسائل مهارات التفكير العليا - 8 (x) = 7x − 11, h(x) = ½-½ x + 11 (59 floga x= logb x logb a (47) مسألة مفتوحة : اكتب مثالًا على عبارة لوغاريتمية لكل حالة مما يأتي، ثم عبّر عنه بالصورة المطولة: (a لوغاريتم حاصل ضرب وقسمة. لوغاريتم حاصل ضرب وقوة. حُلّ كل معادلة مما يأتي وتحقق من صحة حلك (الدرس (2-2) 35x . 811 - x = 9x - 3 (61 log2 (x + 6) = 5 (63 49x = 34x=33-x (60 7x²-15 (62 تدريب على اختبار 2 log 5 12-log 58 - 2 log 5 3 (64 ما قيمة log 53 C 1 D log52 A log50.5 B ؟ لوغاريتم حاصل ضرب وقسمة وقوة. (48) برهان: استعمل خصائص الأسس لبرهنة خاصية لوغاريتم القوة. (65) ما المقطع لا للدالة اللوغاريتمية 3 + (1+y = log2 (x؟ (49) تحد أوجد القيمة الدقيقة للعبارة اللوغاريتمية (2) log Va 3A 2B 1C O D وزارة التعليم الدرس 4- خصائص اللوغاريتمات Ed - 109 2024-1446