المستطيل - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
رابط الدرس الرقمي www.ien.edu.sa A L D L ## المستطيل ABCD أضف إلى مطويتك وزارة التعليم Ministry of Education 2024-1446 M B C Q Ꭱ المستطيل Rectangle 5-4 فيما سبق الماذا؟ أحمد هو الطالب المسؤول عن عرض لوحات الرياضيات في يوم النشاط درست استعمال خصائص المدرسي. ولعمل خلفية مميزة يعرض عليها لوحات الرياضيات، قام بطلاء جزء متوازي الأضلاع وتحديد من جدار على شكل مستطيل يبدأ طوله من أسفل الجدار ويمتد للأعلى، وكان ما إذا كان الشكل الرباعي متوازي أضلاع (الدرس (2-5) والان . أتعرف خصائص المستطيل وأطبقها. أحدد ما إذا كان متوازي الأضلاع مستطيلا. المفردات: المستطيل rectangle طوله 80in ، وعرضه 36in. كيف يمكنه أن يتحقق من أن الجزء الذي قام بطلائه مستطيل ؟ خصائص المستطيل : المستطيل هو متوازي أضلاع زواياه الأربع قوائم. ونجد من ذلك أن للمستطيل الخصائص الآتية : الزوايا الأربع قوائم. . كل ضلعين متقابلين متوازيان ومتطابقان. . كل زاويتين متقابلتين متطابقتان. . كل زاويتين متحالفتين متكاملتان. . القطران ينصف كل منهما الآخر. وبالإضافة إلى ذلك، قطرا المستطيل متطابقان، كما توضح النظرية الآتية: نظرية 5.13 قطرا المستطيل إذا كان متوازي الأضلاع مستطيلا ، فإن قطريه متطابقان. مثال : إذا كان JKLM مستطيلا ، فإن JL = MK . K سوف تبرهن النظرية 5.13 في السؤال 33 . مثال 1 من واقع الحياة استعمال خصائص المستطيل حدائق حديقة مستطيلة الشكل تحتوي على ممرين كما في الشكل المجاور. إذا كان PR = 200m، فأوجد QT قطرا المستطيل متطابقان تعريف تطابق القطع المستقيمة بالتعويض QS = PR QS = PR QS = 200 وبما أن PQRS مستطيل، لذا فإن قطريه ينصف كل منهما الآخر؛ لذا بالتعويض QT= =QS QT = { (200) = 100 تحقق من فهمك استعن بالشكل في المثال 1. (1) إذا كان 120 = TS ، فأوجد PR. (13) إذا كان 64 = mPRS، فأوجد mLSQR. الفصل 5 الأشكال الرباعية 166

إرشادات للدراسة الزوايا القوائم تذكر من النظرية 5.6 أنه إذا كانت إحدى زوايا متوازي الأضلاع قائمة يمكنك استعمال خصائص المستطيل والجبر لإيجاد قيم مجهولة. مثال 2 استعمال خصائص المستطيل والجبر جبر: الشكل الرباعي JKLM مستطيل. إذا كان " (4 + mKJL = (2x و " (5 + mJLK = (7x، فأوجد قيمة x. فإن زواياه الأربع قوائم بما أن JKLM مستطيل، فإن زواياه الأربع قوائم؛ إذن °90 = mZMLK. إرشادات للدراسة الزاويتان المتبادلتان داخليا بالنسبة لقطر: درست سابقا في نظرية الزاويتان المتبادلتان داخليا أنه إذا قطع قاطع مستقيمين متوازيين فإن كل زاويتين متبادلتين داخليا متطابقتان، وينطبق هذا على الزاويتين المتبادلتين بالنسبة لقطر متوازي الأضلاع مثال: 31 21 = 2, 3 = 24 وبما أن JKLM المستطيل متوازي أضلاع، فإن الأضلاع المتقابلة متوازية، والزوايا المتبادلة داخليا بالنسبة للقطر متطابقة. لذا فإن KIL = ، ومن ذلك mZILM = mZKJL. mZJLM+mZJLK=mZMLK mZKJL+mZJLK = 90° مسلمة جمع الزوايا بالتعويض 90° = 5° + 7x) + 24° بالتعويض (9x + 9° = 90° 9x° = 81° x=9 تحقق من فهمك بجمع الحدود المتشابهة بطرح 9 من كلا الطرفين بقسمة كلا الطرفين على 9 K 2) استعن بالشكل في المثال 2. إذا كان 1 + 5 = JP = 3y - 5, MK، فأوجد قيمة y. إثبات أن متوازي أضلاع يكون مستطيلا عكس النظرية 5.13 صحيح أيضًا. نظرية 5.14 إذا كان قطرا متوازي أضلاع متطابقين فإنه مستطيل. W مثال في DWXYZ ، إذا كان WY = XZ أضف إلى مطويتك M AMAJRASH 17 الربط مع الحياة كرة الطائرة هي رياضة جماعية يتنافس فيها فريقان، لكل منهما ستة لاعبين، أما الكرة المستخدمة في هذه اللعبة، فهي متوسطة الحجم وأصغر من كرة القدم وأخف منها وزنًا. فإن DWXYZ مستطيل. سوف تبرهن هذه النظرية في السؤال 34. Z Y مثال 3 من واقع الحياة إثبات علاقات في المستطيل كرة طائرة : أنشأ نادٍ رياضي ملعبا لكرة الطائرة، وللتأكد من أنه يحقق المواصفات المطلوبة، قاس المشرفون أطوال أضلاع الملعب وقطريه، فإذا كان AB = 60 ft, BC = 30 ft, CD = 60 ft, AD = 30 ft ، BD = 67 ft ، AC = 67 ft ، فكيف يمكنهم التحقق من أنه مستطيل. B LAB = CD, BC = AD, AC = BD AB = CD, BC = AD, AC = BD AB CD, BC = AD، فإن ABCD متوازي أضلاع. ولأن AC, BD قطران متطابقان في ABCD، فإنّ ABCD مستطيل. الدرس 4-5 المستطيلة الت167يم Ministry of Education: 2024-1446

كرة الطائرة هي رياضة جماعية يتنافس فيها فريقان
تحقق من فهمك 3) تصميم بالرجوع إلى فقرة "لماذا؟ " بداية الدرس. قاس أحمد أبعاد المنطقة التي قام بطلائها كما في الشكل أدناه. وباستعمال زاوية النجارين تحقق من أن الزاوية عند الركن الأيسر السفلي قائمة. فهل يمكنه استنتاج أن المنطقة مستطيلة الشكل ؟ وضّح إجابتك. 36 in الربط مع الحياة زاوية النجارين عبارة عن ضلع خشبي سميك ومسطرة معدنية مثبتة معه بحيث يصنعان زاوية 90 ، وتصنع من المعدن أو الخشب وتستخدم لقياس 80 in 80 in 36 in وتحديد الزوايا القائمة يمكنك أيضًا استعمال خصائص المستطيل لإثبات أن شكلاً رباعيًا مرسوما في المستوى الإحداثي عُلمت ورسم خطوط عمودية على إحداثيات رؤوسه هو مستطيل. الأحرف. مثال 4 المستطيل والهندسة الإحداثية هندسة إحداثية: إذا كانت إحداثيات رؤوس الشكل الرباعي PQRS هي 170-R ,1 ,1 ,(53). فهل PQRS مستطيل ؟ استعمل صيغة المسافة بين نقطتين. الخطوة 1: استعمل صيغة المسافة بين نقطتين لتحدد ما إذا كان PQRS متوازي أضلاع، وذلك بالتحقق من أن أضلاعه المتقابلة متطابقة. 10 Ay R إرشادات للدراسة المستطيل ومتوازي الأضلاع كل مستطيل متوازي أضلاع، ولكن ليس كل متوازي أضلاع مستطيلا. PQ=√(-51)²+ [3-(-1)]² = √52 RS = V[-1 - (-7) 2 + ( -4 - 02 = √52 PS = [-5-(-7)]² + (3-0)² = √13 QR = 1 [1-(-1)]² + [-1-(-4)]² = √√13 بما أن أضلاع PQRS المتقابلة متساوية الطول، فإنّها متطابقة؛ لذا فإن PQRS متوازي أضلاع. الخطوة 2 هل قطرا PQRS متطابقان؟ 168 الفصل 5 الأشكال الرباعية PR = V[-5 - (-1) 2 + [3 - (4) 2 QS = = √65 1-(-7)]2+(-1-0)² = √√65 بما أن للقطرين الطول نفسه، فإنّهما متطابقان؛ لذا فإن PQRS مستطيل. تحقق من فهمك 4) إذا كانت إحداثيات رؤوس الشكل الرباعي هي (25) 33 ,25 ,8-) ,(2 ,10). فهل JKLM مستطيل ؟ استعمل صيغة الميل. S وزارة التعليم Ministry of Education 2024-1446

زاوية النجارين
MX F D E المثال 1 زراعة الشكل المجاور يبيّن بوّابة مخزن حبوب مستطيلة الشكل فيها الدعامتان المتقاطعتان تقويان دفة البوابة، وتحفظانها من الالتواء مع مرور الزمن. 13 ،PS = 7 ft, ST = 3 إذا كان °67 = ft, mPTQ 3 SQ (2 mZTSR (4 فأوجد كلًا مما يأتي : QR (1) mZTQR (3 المثال 2 جبر: استعن بالمستطيل DEFG المبين جانبًا. إذا كان 5 + FD = 3x - , EG = x، فأوجد EG. (6) إذا كان " (12) + (m/EFD = (2x - 3) ", mLDFG = (x، فأوجد mLEFD. المثال 3 (7) برهان : إذا كان ABDE مستطيلا، و BC = DC، فأثبت أن AC = EC . هندسة إحداثية: مثل في المستوى الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه في كل من السؤالين الآتيين، وحدد ما إذا كان مستطيلا أم لا . برر إجابتك باستعمال الطريقة المحددة في السؤال. Y P W X all W(-4, 3), X(1, 5), Y(3, 1), Z(-2, -2) (8 A(4, 3), B(4, -2), C(-4, -2), D(-4, 3) (9 المثال 4 تأكد تدرب وحل المسائل المثال 1 سياج سياج مستطيل الشكل تُستعمل فيه دعائم متقاطعة لتقوية السياج. إذا كان 65 = AB = 6ft, AC = 2 ft, mL CAE CB (11 mZECD (13 فأوجد كلا مما يأتي : BD (10 mZDEB 12 المثال 2 جبر: استعن بالمستطيل WXYZ المبيَّن جانبًا. (14) إذا كان 4 + ZY = 2x + 3 + WX = x، فأوجد WX . (15) إذا كان 11 + PY = 3x - 5, WP = 2x، فأوجد ZP. mZZYW= (2x-7), mZWYX = (2x+5)° 35 13 (16 فأوجد mZZYW. (17) إذا كان 5 + ZP = 4x - , PY = 2x، فأوجد ZX. 18) إذا كان 12 - mXZY = (3x + (6°, mXZW = (5x، فأوجد mYXZ. 19) إذا كان (9) - mZZXW = (x-11)°, mWZX = ( x، فأوجد mZZXY. الدرس 4-5- المستطيلة الـ169يم Ministry of Education 2024-1446

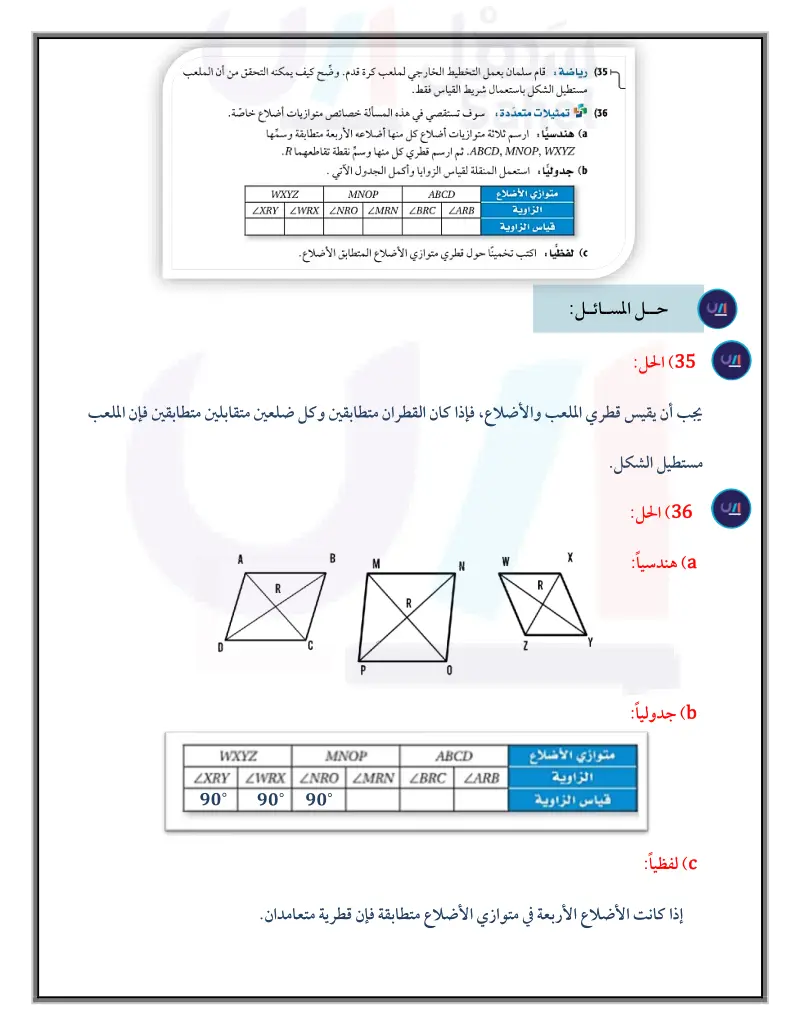
الشكل المجاور يبين بوابة مخزن حبوب مستطيلة الشكل فيها الدعامتان المتقاطعتان تقويان دفة البوابة وتحفظها من الالتواء مع مرور الزمن، أوجد كلا مما يأتي


B المثال 3 برهان اكتب برهانا ذا عمودين في كل مما يأتي: (20) المعطيات ABCD مستطيل. المطلوب AADC = ABCD (21) المعطيات QTVW مستطيل. QR = ST المطلوب ASWQ = ARVT W R S A T V D B C المثال 4 هندسة إحداثية : مثل في المستوى الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه في كل مما يأتي، وحدد ما إذا كان مستطيلا أم لا . برر إجابتك باستعمال الطريقة المحددة في السؤال. 8 6 M N JW(-2, 4), X(5, 5), Y(6, -2), Z(-1,-3) (22 • juke joiden J(3, 3), K(−5, 2), L(-4, -4), M(4, -3) (23 15 in. P 0 15 in. Q R 3 ft 24) (45) ,(56,1 ,2 ,R1 ,2 ,2 - ) ، صيغة المسافة بين نقطتين. m23 (28) mZ8 (31 G(1, 8), H(-7, 7), J(-6, 1), K(2, 2) (25 في المستطيل ABCD ، إذا كان 40 = m2 ، فأوجد كلا مما يأتي : m27 (27 mZ6 (30 m21 (26 m25 (29 (32) مكتبات أضاف زيد رقًا جديدًا لمكتبته ودعائم معدنية متقاطعة كما في الشكل المجاور . كم يجب أن يكون طول كل من الدعائم المعدنية بحيث تكون الرفوف عمودية على الجانبين؟ وضح إجابتك. إرشاد: 12in = 1ft) برهان اكتب برهانا ذا عمودين لإثبات النظرية في كل من (34) النظرية 5.14 السؤالين الآتيين : (33) النظرية 5.13 الربط مع الحياة 35) رياضة : قام سلمان بعمل التخطيط الخارجي لملعب كرة قدم. وضّح كيف يمكنه التحقق من أن الملعب مستطيل الشكل باستعمال شريط القياس فقط. حددت رابطة كرة القدم (36) تمثيلات متعددة : سوف تستقصي في هذه المسألة خصائص متوازيات أضلاع خاصة. الدولية (IFAP) الأبعاد القياسية لملعب كرة القدم في البطولات الرسمية الدولية فكانت 105m طولا، و 68m عرضًا. a) هندسيا : ارسم ثلاثة متوازيات أضلاع كل منها أضلاعه الأربعة متطابقة وسمها ABCD, MNOP, WXYZ. ثم ارسم قطري كل منها وسم نقطة تقاطعهما .R. جدوليًا: استعمل المنقلة لقياس الزوايا وأكمل الجدول الآتي . وزارة التعليم Ministry of Education 2024-1446 متوازي الأضلاع الزاوية قياس الزاوية ABCD ZARB MNOP WXYZ ZXRY ZWRX ZNRO ZMRN ZBRC لفظيا : اكتب تخمينا حول قطري متوازي الأضلاع المتطابق الأضلاع الفصل 5 الأشكال الرباعية 170

تدرب مثل في المستوى الاحداثي الشكل الرباعي المعطاة احداثيات رؤوسه في كل من السؤالين الآتيين. وحدد ما إذا كان مستطيلا ام لا. برر اجابتك باستعمال الطريقة المحددة في السؤال


حددت رابطة كرة القدم الدولية الأبعاد القياسية لملعب كرة القدم في البطولات الرسمية الدولية فكانت 105m طولا و 68m عرضا
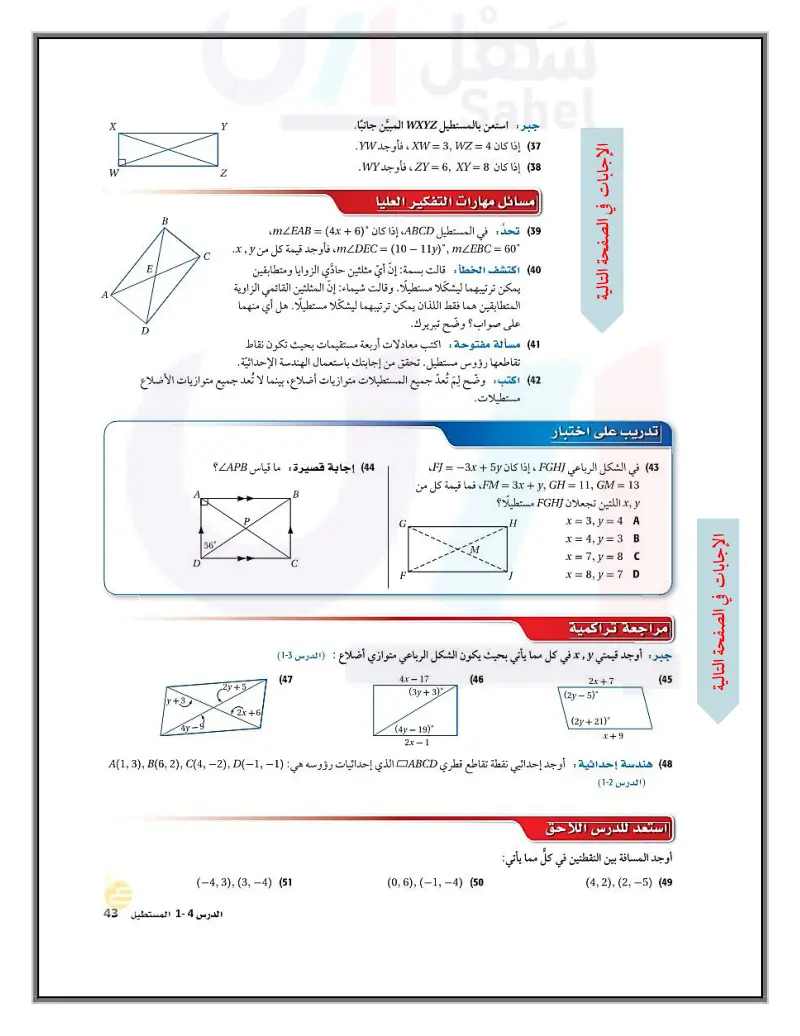
جبر: استعن بالمستطيل WXYZ المبيَّن جانبًا. (37) إذا كان 4 = XW = 3, WZ ، فأوجد YW. (38) إذا كان 8 = ZY = 6 XY ، فأوجد WY. مسائل مهارات التفكير العليا (39) تحد في المستطيل ABCD ، إذا كان (6 + mEAB = (4x، "60 = mDEC = (10) - 11y) ", mLEBC ، فأوجد قيمة كل من x (40) اكتشف الخطأ : قالت بسمة: إنّ أيّ مثلثين حادي الزوايا ومتطابقين يمكن ترتيبهما ليشكّلا مستطيلا . وقالت شيماء: إنّ المثلثين القائمي الزاوية المتطابقين هما فقط اللذان يمكن ترتيبهما ليشكلا مستطيلا. هل أي منهما على صواب؟ وضح تبريرك. (41) مسألة مفتوحة : اكتب معادلات أربعة مستقيمات بحيث تكون نقاط تقاطعها رؤوس مستطيل. تحقق من إجابتك باستعمال الهندسة الإحداثية. X Y Z B E C D 42) اكتب: وضح لِمَ تُعدّ جميع المستطيلات متوازيات أضلاع، بينما لا تُعد . . جميع متوازيات الأضلاع مستطيلات. W A D تدريب على اختبار 43) في الشكل الرباعي (FGH ، إذا كان 5 + FJ = 3x 13 = FM = 3x + y, GH = 11, GM، فما قيمة كل من , اللتين تجعلان FGHJ مستطيلا؟ 44 إجابة قصيرة: ما قياس LAPB؟ B 56% P C H x = 3, y = 4 A x = 4, y = 3 B x = 7, y = 8 x = 8, y = 7 D مراجعة تراكمية جبر أوجد قيمتي , x في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع : ( الدرس 3-5) (47 2y+5 y+3 2x+6 4x - 17 (3y+3) (4y-19)° 2x - 1 (46 2x+7 (2y-5)° (2y+21)° x+9 (45 (48) هندسة إحداثية: أوجد إحداثيي نقطة تقاطع قطري ABCD الذي إحداثيات رؤوسه هي: (2011 ,4)A(1,3), B(6, 2), C (الدرس (2-5) (-4, 3), (3,-4) (51) (0, 6), (-1,-4) (50 الدرس 4-5- المستطيلة الت171يم Ministry of Education 2024-1446 استعد للدرس اللاحق أوجد المسافة بين النقطتين في كل مما يأتي: (4,2), (2,-5) (49