المتباينات في المثلث - رياضيات 1-2 - أول ثانوي

4-3 المتباينات في المثلث Inequalities in One Triangle الماذا؟ فيما سبق درست العلاقة بين قياسات يستعمل المصممون طريقة تُسمى التثليث؛ لإعطاء زوايا المثلث. الغرفة مظهرًا يُوحي بالاتساع، ومن الأمثلة على هذه الطريقة وضع طاولة صغيرة عند كل طرف من طرفي وانان - أتعرف خصائص أريكة مع وضع لوحة فوقها. على أن يكون قياس كل زاوية من زاويتي قاعدة المثلث أقل من قياس الزاوية المتباينات، وأطبقها على قياسات زوايا المثلث. الثالثة. " www.ien.edu.sa أطبق خصائص المتباينات على العلاقة متباينات الزوايا : تعلمت في الجبر المتباينة بوصفها علاقة بين عددين حقيقيين، وتُستعمل هذه العلاقة عادة في البراهين. بين زوايا مثلث وأضلاعه. مفهوم أساسي تعريف المتباينة التعبير اللفظي لأي عددين حقيقيين مثل يكون a b ، إذا وفقط إذا وجد عدد حقيقي أضف إلى طويتك موجب C على أن يكون a = b + c مثال إذا كان 3 + 2 = 5 ، فإن 52 وفي الجدول أدناه قائمة ببعض خصائص المتباينات التي درستها. مفهوم أساسي أضف إلى خصائص المتباينة على الأعداد الحقيقية الخصائص الآتية صحيحة لأي ثلاثة أعداد حقيقية abc خاصية المقارنة a<bia=bia > b خاصية التعدي 1) إذا كان abb ، فإن a خاصية الجمع (1) إذا كان a c . (2) إذا كان a b ، فإن a c . b ، فإن a b c . (2) إذا كان a b ، فإن a + cbc . خاصية الطرح 1) إذا كان a (2) إذا كان a b ، فإن a - b - c b ، فإن a - b - c يمكن أن يطبق تعريف المتباينة وخصائصها على قياسات الزوايا وأطوال القطع المستقيمة؛ لأنها أعداد حقيقية. تأمل 123 في الشكل المجاور. من نظرية الزاوية الخارجيّة، تعلم أنّ m1 = m2 + m3 وبما أن قياسات الزوايا أعداد موجبة، إذن نستنتج أن: mZ1 > m23 وهذه النتيجة تقود إلى النظرية الآتية: و mZ1 > m2 طويتك الدرس 3-4 المتباينات في المثلث الت99 2024-1446

مراجعة المفردات الزاويتان الداخليتان البعيدتان نظرية 4.8 متباينة الزاوية الخارجية قياس الزاوية الخارجية لمثلث أكبر من قياس أي من الزاويتين الداخليتين البعيدتين عنها. لكل زاوية خارجية لمثلث زاويتان داخليتان بعيدتان وهما الزاويتان مثال: غير المجاورتين لها. m1 > mZA mZ1 > mZB أضف إلى طوبتك C 1 B A ستبرهن هذه النظرية في الدرس 4-4 مثال 1 استعمال نظرية متباينة الزاوية الخارجية استعمل نظرية متباينة الزاوية الخارجية؛ لكتابة جميع الزوايا المرقمة التي تحقق الشرط المعطى في كل مما يأتي: a) قياساتها أقل من m27 7 زاوية خارجية لـ AKML ، والزاويتان 45 هما الزاويتان الداخليتان البعيدتان عنها، وبناءً على نظرية متباينة الزاوية الخارجية يكون .m27 m24, mZ7> mZ5 K 28 3 5 M وكذلك 27 زاوية خارجية لـ AJKL ، والزاويتان 1KL هما الزاويتان الداخليتان البعيدتان عنها؛ لذا فإن m27 > m1 m7 > mJKL . وبما أنّ mJKL = m2 + m4 ، وبالتعويض يكون 4 + m2 < 7 ؛ إذن m27 > m2. لذا فالزوايا التي قياساتها أقل من m27 هي 1245 قياساتها أكبر من m6 3 زاوية خارجية لـ AKLM . وبناءً على نظرية متباينة الزاوية الخارجية يكون m3 > m6 . وبما أن 8 زاوية خارجية لـ AJKL ، فإن m8 m6 ؛ لذا فقياس كل من 38 أكبر من m6 . تحقق من فهمك 1) قياساتها أقل من m1 (13) قياساتها أكبر من m28 R 1 8 P تنبيه ! العلاقات بين زوايا المثلث وأضلاعه في الدرس ، تعلمت أنه إذا تطابق ضلعان في مثلث، فإن الزاويتين المقابلتين لهذين الضلعين متطابقتان . ولكن كيف تكون العلاقة إذا كان الضلعان غير متطابقين. وللإجابة عن هذا السؤال افحص أطول الأضلاع وأقصرها وأصغر الزوايا وأكبرها لمثلث منفرج الزاوية تحديد الضلع المقابل ومختلف الأضلاع. انتبه عند تحديد الضلع المقابل لزاوية بصورة صحيحة، فالضلعان اللذان يشكلان الزاوية لا يمكن أن يكون أحدهما مقابلا لها. أطول ضلع B C أقصر ضلع B أصغر زاوية - A 100 أكبر زاوية لاحظ أن أطول ضلع في AABC يقابل أكبر زاوية، وبالمثل فإن أقصر ضلع يقابل أصغر زاوية أيضًا . وزارة التعليم الفصل 4 العلاقات في المثلث Ministry of Education 2024-1446

تنبيه ! رمزا الزاوية والمتباينة يبدو رمز الزاوية (2) مشابها لرمز أقل من >)، وخاصة عند الكتابة باليد؛ لذا كن دقيقا في كتابة الرموز بصورة صحيحة عندما يُستعمل الرمزان معا. إن العلاقات بين الزوايا والأضلاع في المثلث المنفرج الزاوية والمختلف الأضلاع تكون صحيحة لجميع المثلثات، ويمكن صياغتها باستعمال المتباينات في النظريتين الآتيتين: نظريتان 4.9 4.10 العلاقات بين زوايا المثلث وأضلاعه متباينة ضلع - زاوية : إذا كان أحد أضلاع مثلث أطول من ضلع آخر، فإن قياس الزاوية المقابلة للضلع الأطول يكون أكبر من قياس الزاوية المقابلة للضلع الأقصر. مثال بما أن X Y Z ، فإن mZZ > mz. متباينة زاوية - ضلع : إذا كان قياس إحدى زوايا مثلث أكبر من قياس زاوية أخرى، فإن الضلع المقابل للزاوية الكبرى يكون أطول من الضلع المقابل للزاوية الصغرى. مثال بما أن mJ> mK ، فإن KL L . Y أضف إلى مطويتك L /110° K 45° D B برهان النظرية 4.9 المعطيات : AABC ، فيه AB BC . المطلوب : mZBCA > mLA. البرهان : بما أن AB > BC في AABC ، فإنه توجد نقطة D على AB بحيث BD - BC ؛ لذا ارسم CD لتشكل ABCD المتطابق الضلعين، وبناءً على نظرية المثلث المتطابق الضلعين تكون 2 = 1 ، واستنادًا إلى تعريف تطابق الزوايا يكون m1 = m2 A واعتمادًا على مسلمة جمع قياسات الزوايا يكون mBCA = m2 + m3 ، إذن MBCA > m2 بحسب تعريف المتباينة. وبالتعويض ينتج أن MBCA > m1 . وبناءً على نظرية متباينة الزاوية الخارجية يكون m1 > mLA . وبما أن MBCA > m1, m1 > mZA ، فإن BCAA MA بحسب خاصية التعدي للمتباينة. P 8.8 Q 7.5 9.1 R 3.7 ستبرهن النظرية 4.10 في الدرس 4-4 مثال 2 ترتيب زوايا المثلث وفقًا لقياساتها اكتب زوايا APQR مرتبةً من الأصغر إلى الأكبر. الأضلاع مرتبة من الأقصر إلى الأطول هي : PR, PQQ. والزوايا المقابلة لهذه الأضلاع هي : على الترتيب؛ لذا فالزوايا مرتبةً من الأصغر إلى الأكبر تكون على النحو الآتي: A 4.8 B 7 C الدرس 3-4 المتباينات في المثلثات ال101م Ministry of Ex 2024-1446 تحقق من فهمك (2) اكتب زوايا AABC مرتبةً من الأصغر إلى الأكبر.

F مثال 3 ترتيب أضلاع المثلث وفقًا لأطوالها اكتب أضلاع AFGH مرتبةً من الأقصر إلى الأطول. أوجد قياس الزاوية المجهولة باستعمال نظرية مجموع قياسات زوايا المثلث. mZF = 180 - (45° + 56) = 79° لذا فالزوايا مرتبة من الأصغر إلى الأكبر هي : GF والأضلاع المقابلة لهذه الزوايا هي: FH ,FGH على الترتيب. إذن فالأضلاع مرتبة من الأقصر إلى الأطول تكون على النحو التالي: FH FG GH. 45° 56 G H W 51 Y X تحقق من فهمك (3) اكتب زوايا AWXY وأضلاعه، مرتبةً من الأصغر إلى الأكبر. ويمكنك استعمال العلاقات بين الزوايا والأضلاع في المثلثات لحل مسائل من واقع الحياة. مثال 4 من واقع الحياة العلاقات بين الزوايا والأضلاع C تصميم داخلي : يستعمل مصمّم فكرة التثليث الواردة في فقرة لماذا؟ لترتيب غرفة الاستقبال. فإذا أراد المصمّم أن يكون mB أقل من mA ، فأي مسافة يجب أن تكون أطول المسافة بين المصباحين أم المسافة بين النقطتين A ,C؟ فسر إجابتك. A بحسب نظرية متباينة زاوية - ضلع ، لكي يكون MB < mLA ، يجب أن يكون طول الضلع المقابل لـ B أقصر من طول الضلع المقابل لـ A . وبما أن AC يقابل B و BC يقابل A ، فإن AC < BC ؛ لذا فالمسافة BC بين المصباحين ستكون أكبر من المسافة بين النقطتين A,C وزارة التعليم Ministry of Education 2024-1446 المدرب /60° 59° المتدرب الثاني المتدرب الأول الربط مع الحياة برامج إعداد المنقذين في السباحة تتضمن تدريبا على المراقبة والإنقاذ والإسعافات الأولية، وتتراوح مدة البرنامج عادة ما بين 30 إلى 37 ساعة تبعا لطبيعة الوسط المائي مثل البرك أو شواطئ البحار. تحقق من فهمك (4) سباحو الإنقاذ : في أثناء التدريب يُمثل المدرب دور شخص في خطر ليتمكن المتدربان من تطبيق مهارات الإنقاذ. إذا كان المدرّب والمتدربان الأول والثاني في المواقع المبينة في الشكل، فأي المتدربين أقرب إلى المدرب ؟ الفصل 4 العلاقات في المثلث 102

34 65 8 9 المثال 1 استعمل نظرية متباينة الزاوية الخارجيّة، لكتابة جميع الزوايا المرقمة التي تحقق الشرط المعطى في كل مما يأتي : (1) قياساتها أقل من m4 . 2) قياساتها أكبر من m27 (3) قياساتها أكبر من m22 (4) قياساتها أقل من m29 . المثالان 23 اكتب زوايا كل مثلث مرتبةً من الأصغر إلى الأكبر في السؤالين الآتيين : (6) 46 K 87 L A 3.1 2.8. (5 B 1.7 C المثال 4 (7) طيران شراعي: تشكل دعائم الطائرة الشراعية مثلثات كالمثلث الظاهر في الصورة . فأي دعامة تكون أطول: AC أم BC ؟ وضح إجابتك. تأكد تدرب وحل المسائل المثال 1 استعمل نظرية متباينة الزاوية الخارجية؛ لكتابة جميع الزوايا المرقمة التي تحقق الشرط المُعطَى في كل مما يأتي: 8 قياساتها أكبر من m2 . 9) قياساتها أقل من m4 . 10) قياساتها أقل من m29 . 27 8 9 A B (14 \51° الدرس 3-4 - المتباينات في المثلثات ال103 Ministry of E 2024-1446 11) قياساتها أكبر من m28 . المثالان 2 اكتب زوايا كل مثلث مرتبةً من الأصغر إلى الأكبر في كل مما يأتي: H 57° 62' K 61° (13 Y (12 2.3 W 3.4 Z

المثال 4 (15) كرة قدم يقف أحمد وخالد وماهر في ملعب (16 منحدرات يمثل المنحدر طريقا للدراجات كرة قدم كما في الشكل أدناه، ويريد ماهر أن يمرر الهوائية. فأيهما أطول؛ طول المنحدر XZ أم طول الكرة إلى أحد زميليه، على أن تكون مسافة التمرير السطح العلوي للمنحدر YZ ؟ وضح إجابتك أقصر. أيهما يختار خالدًا أم أحمد؟ برر إجابتك. باستعمال النظرية 4.9. خالدي X X Y (2x+9) (2x + 1) 5 4 10 12 13 9 1114 A 3 B 14 C 15 13 12 11 D 5 F M P 70° 30° 148° 8 الربط مع الحياة بينت إحدى الدراسات أن فريق كرة القدم يصبح في حالة الهجوم ما بين 45-65 مرة في المباراة الواحدة. 17 اكتب زوايا المثلث المجاور مرتبةً من الأصغر إلى الأكبر : استعمل الشكل المجاور؛ لتحدّد الزاوية ذات القياس الأكبر والفريق المتميز هو الذي يتميز بقدرته على تنفيذ الهجمات بشكل جيد وفي الوقت نفسه يستطيع الاحتفاظ بدفاع متماسك. في كل مجموعة مما يأتي : Z2, 24, 26 (19 23, 211, Z12 (21 Z8, 210, Z11 (23 21, 25, 26 (18 27, 24, 25 (20 Z3, Z9, Z14 (22 استعمل الشكل المجاور؛ لتحدد العلاقة بين قياسات الزوايا المعطاة في كل من الأسئلة الآتية : ZBCF, ZCFB (25 ZABD, ZBDA (24 ZDBF, ZBFD (27 ZBFD, ZBDF (26 استعمل الشكل المجاور؛ لتحدد العلاقة بين أطوال الأضلاع المعطاة 60° 1107 85 RQ, PQ (30 RP, MP (29 V S R Q A B 62° 71° وزارة التعليم Ministry of Education 2024-1446 10 C 83° 42° 12 D في كل من الأسئلة الآتية: SM, MR (28) (31) اكتب أضلاع كل مثلث في الشكل المجاور مرتبة من الأقصر إلى الأطول. ووضح إجابتك. الفصل 4 العلاقات في المثلث 104

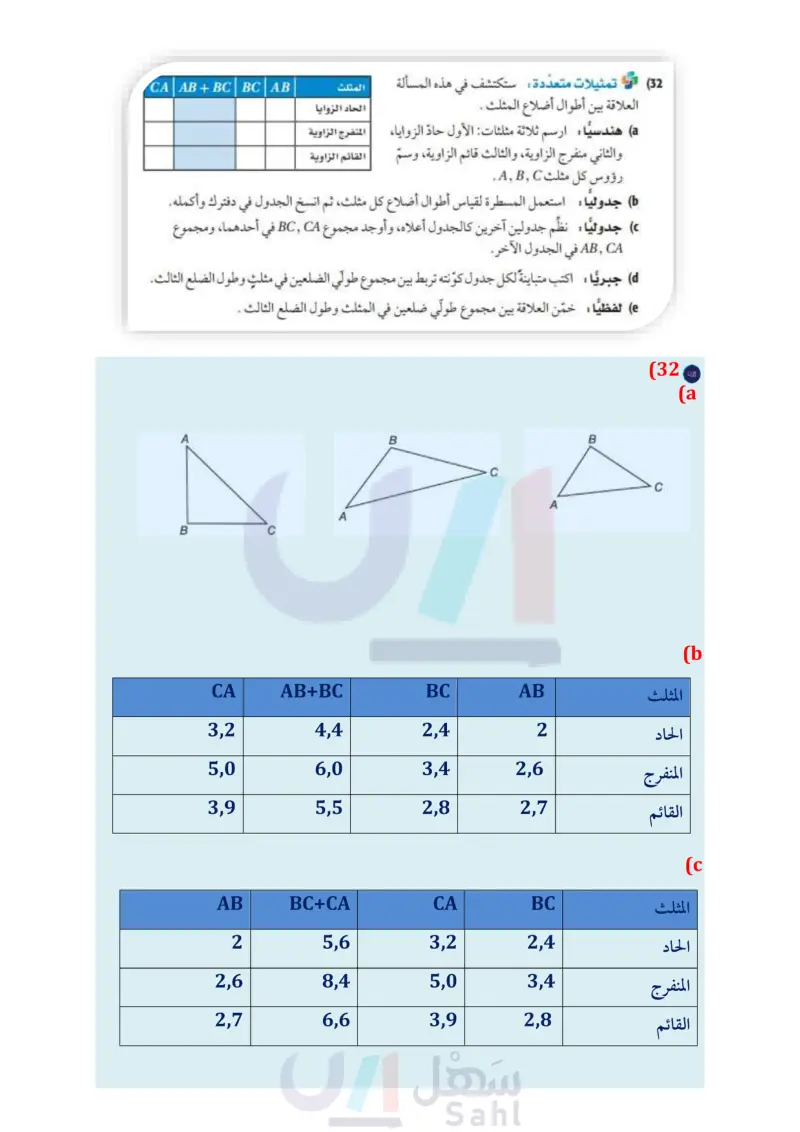
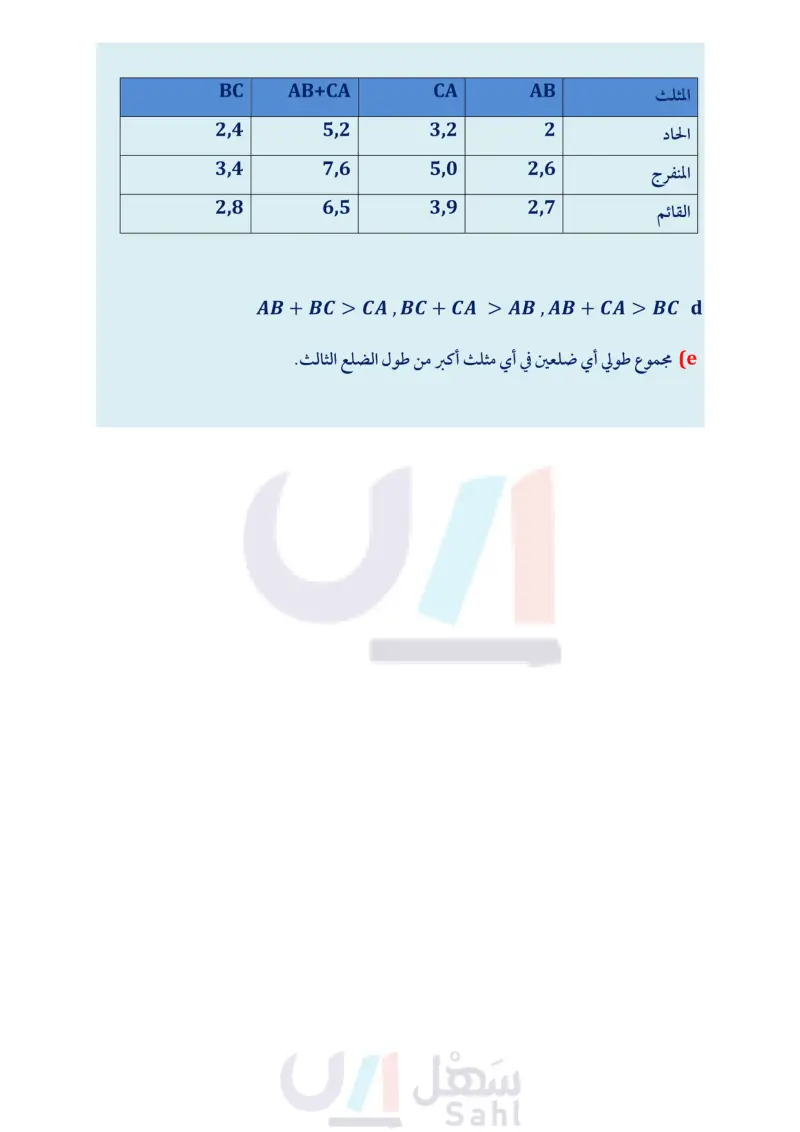
تدريب على اختبار (32) تمثيلات متعددة ستكتشف في هذه المسألة العلاقة بين أطوال أضلاع المثلث . المثلث الحاد الزوايا (a) هندسيا : ارسم ثلاثة مثلثات: الأول حاد الزوايا، المنفرج الزاوية والثاني منفرج الزاوية، والثالث قائم الزاوية، وسمّ القائم الزاوية رؤوس کل مثلث . CA | AB + BCBC | AB جدوليا: استعمل المسطرة لقياس أطوال أضلاع كل مثلث، ثم انسخ الجدول في دفترك وأكمله. جدوليا : نظم جدولين آخرين كالجدول أعلاه، وأوجد مجموع BCCA في أ ، أحدهما، ومجموع ABCA في الجدول الآخر. d جبريًا : اكتب متباينة لكل جدول كوّنته تربط بين مجموع طولي الضلعين في مثلث وطول الضلع الثالث. e لفظيا : خمّن العلاقة بين مجموع طولي ضلعين في المثلث وطول الضلع الثالث . مسائل مهارات التفكير العليا (33) تبرير: هل تكون قاعدة المثلث المتطابق الضلعين هي الضلع الأطول في المثلث دائمًا أم أحيانًا أم لا تكون أبدًا؟ وضح إجابتك. (34) تحد: استعمل أطوال الأضلاع في الشكل المجاور؛ لترتب قياسات الزوايا المرقمة من الأصغر إلى الأكبر، إذا علمت أن m2 = m25 . ووضح إجابتك. 10 cm 5 17 cm 2 8 cm 35) اكتب وضح لماذا يكون الوتر في المثلث القائم الزاوية هو الضلع الأطول دائما ؟ 11 cm. 3/4 12 cm (36) إذا كان قياسا زاويتين في مثلث هما "925، فما نوع هذا المثلث؟ (37) أي عبارة عددية مما يأتي لها أصغر قيمة؟ منفرج الزاوية ومختلف الأضلاع. حاد الزوايا ومختلف الأضلاع. منفرج الزاوية ومتطابق الضلعين. حاد الزوايا ومتطابق الضلعين. مراجعة تراكمية 45 A |15 B (38) هندسة إحداثية بصيغة الميل والمقطع اكتب معادلة العمود المنصف للقطعة المستقيمة التي إحداثيات طرفيها (2) الدرس (1-4) (39) طائرات يطير سرب من الطائرات على هيئة مثلثين بينهما ضلع مشترك. اكتب برهانا ذا عمودين " ASRT = AQRT ، إذا كانت النقطة T منتصف SR QR SQ (الدرس (3) الإثبات أن: 1-28 C |-39 D استعد للدرس اللاحق إذا كان 3 = 2 ,2 = x = 8, y ، فحدد ما إذا كانت كل عبارة مما يأتي صحيحةً أم خاطئةً: (x - y = 13 (40) 2x=3yz (41 x+ y> z+y (42) الدرس 3-4 المتباينات في المثلثات ال105 Ministry of Edu 2024-1446

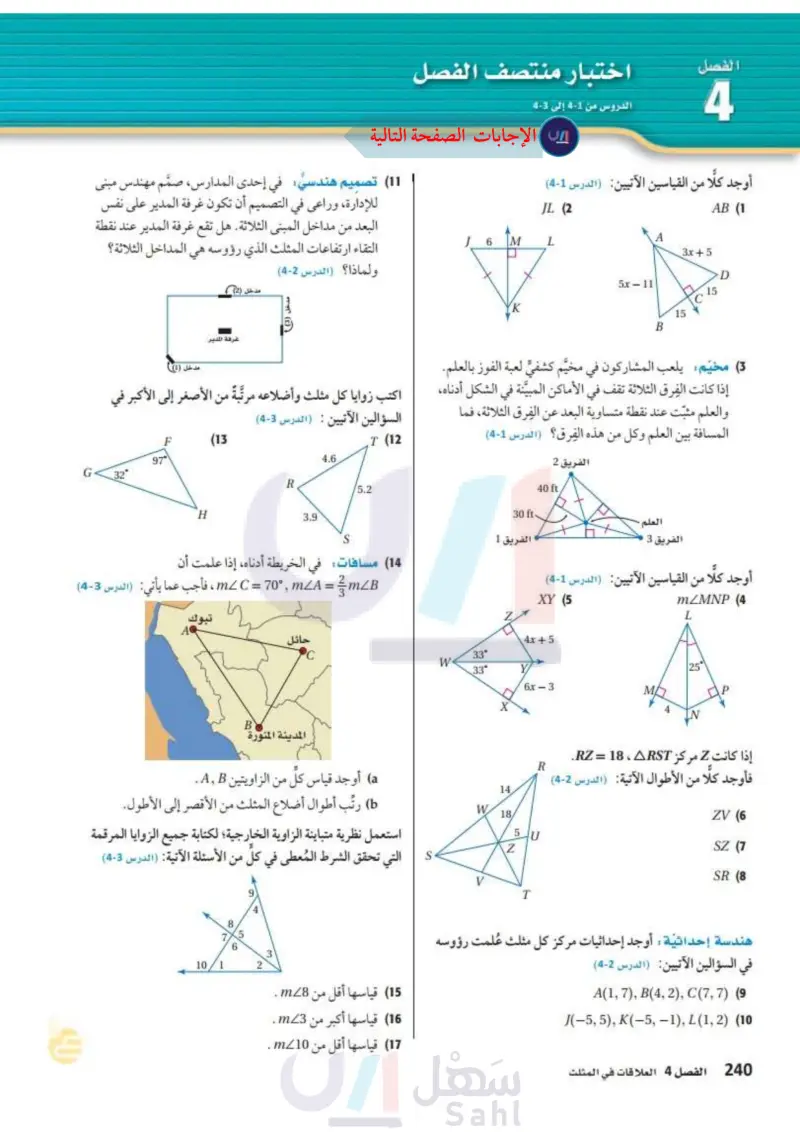
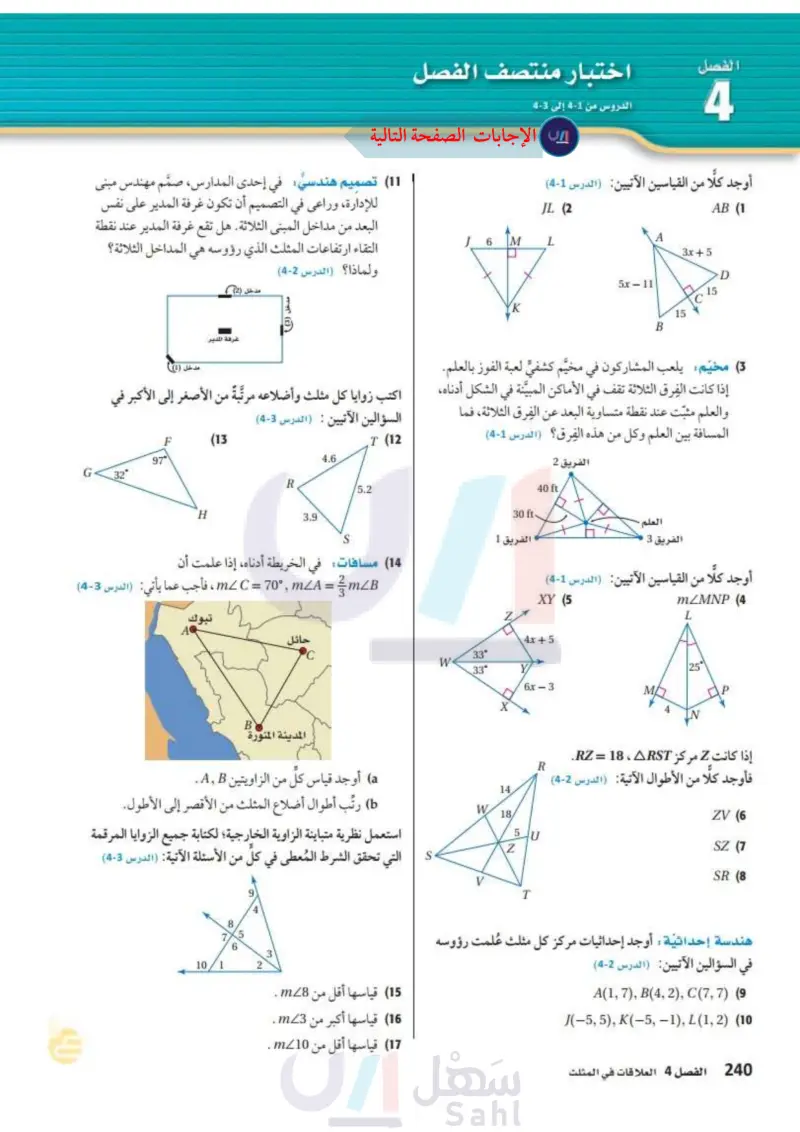
11) تصميم هندسي في إحدى المدارس، صمم مهندس مبنی للإدارة، وراعى في التصميم أن تكون غرفة المدير على نفس البعد من مداخل المبنى الثلاثة هل تقع غرفة المدير عند نقطة التقاء ارتفاعات المثلث الذي رؤوسه هي المداخل الثلاثة؟ ولماذا ؟ (الدرس (2-4) مدخل (2) غرفة المدير اختبار منتصف الفصل الدروس من 1-4 إلى 3-4 الفصل 4 أوجد كلًا من القياسين الآتيين: (الدرس 1-4) JL (2 6 M L AB (1 3x+5 D 50–11 B 15 (3) مخيم يلعب المشاركون في مخيم كشفي لعبة الفوز بالعلم. مدخل (1)) إذا كانت الفرق الثلاثة تقف في الأماكن المبينة في الشكل أدناه، اكتب زوايا كل مثلث وأضلاعه مرتبةً من الأصغر إلى الأكبر في والعلم مثبت عند نقطة متساوية البعد عن الفرق الثلاثة، فما المسافة بين العلم وكل من هذه الفرق؟ (الدرس 1-4) العلم . الفريق 3 الفريق 2 40 ft 30 ft- الفريق 1 السؤالين الآتيين : (الدرس (3-4) T (12 4.6 R /5.2 3.9 S F (13 97° G 32° H 14 مسافات في الخريطة أدناه، إذا علمت أن mL C = 70°, mLA = mB ، فأجب عما يأتي: (الدرس 3-4) وزارة التعليم Ministry of Education 2024-1446 تبوك AQ B أوجد كلا من القياسين الآتيين: (الدرس 1-4) XY (5 21 mZMNP (4 L حائل 4x+5 C W 33° 33° 25° 6x - 3 M X N المدينة المنورة a أوجد قياس كل من الزاويتين A,B. b) رتب أطوال أضلاع المثلث من الأقصر إلى الأطول. استعمل نظرية متباينة الزاوية الخارجية لكتابة جميع الزوايا المرقمة التي تحقق الشرط المُعطى في كل من الأسئلة الآتية: (الدرس (3-4) 5 6 10. إذا كانت 2 مركز RZ = 18 ، RST . فأوجد كلا من الأطوال الآتية: (الدرس (2-4) R 14. W 18/ 5 U Z S V T ZV (6 SZ (7) SR (8 هندسة إحداثية : أوجد إحداثيات مركز كل مثلث عُلمت رؤوسه في السؤالين الآتيين (الدرس (2-4) A(1, 7), B(4, 2), C(7, 7) (9 (-5, 5), K(-5, -1), L(1, 2) (10 (15) قياسها أقل من m8 . (16) قياسها أكبر من m3 . (17) قياسها أقل من m10 . الفصل 4 العلاقات في المثلث 106