المثلثات المتطابقة - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
3-3 المثلثات المتطابقة Congruent triangles فيما سبق درست الزوايا المتطابقة واستعمالاتها. (مهارة سابقة) والان . أُسمي العناصر المتناظرة في المضلعات المتطابقة وأستعملها. . أثبت تطابق مثلثين باستعمال تعريف التطابق ا لماذا؟ تقوم عدة مصانع بصنع مسجلات سيارات بواجهات متحركة يصعب نزعها لحمايتها من السرقة، علما بأن شكل هذه الواجهات وأبعادها تطابق شكل المكان الذي تثبت فيه وأبعاده تمامًا؛ وذلك لتثبيتها في لوحة أجهزة السيارة بدقة. التطابق والعناصر المتناظرة : إذا كان لشكلين هندسيين الشكل نفسه والقياسات نفسها فإنهما متطابقان. المفردات التطابق Congruent المضلعات المتطابقة Congruent Polygons العناصر المتناظرة Corresponding Parts 28 متطابقة الأشكال لها الشكل نفسه والقياسات نفسها، على الرغم من أنها في أوضاع مختلفة. غير متطابقة 4 الشكلان لهما الشكل نفسه، لكنهما مختلفان في القياسات. في أي مضلعين متطابقين تتطابق العناصر المتناظرة، والعناصر المتناظرة تتضمن الزوايا والأضلاع. مفهوم أساسي تعريف المضلعات المتطابقة التعبير اللفظي : يتطابق مضلعان إذا وفقط إذا كانت عناصرهما المتناظرة متطابقة. مثال: الزوايا المتناظرة ZAZH الأضلاع المتناظرة AB = HJ عبارة التطابق C أضف إلى مطويتك نموذج : H ZCZK ZBZJ K CA = KH BC= JK AABC= AHJK B هناك عبارات تطابق أخرى للمثلثين أعلاه، وعبارات التطابق الصحيحة للمضلعات المتطابقة تظهر الرؤوس المتناظرة بالترتيب نفسه. عبارة صحيحة عبارة غير صحيحة الفصل 3 المثلثات المتطابقة ABCA = AJKH 444 44 AABC = AHKJ وزارة التعليم Ministry of Education 2024-1446

S مثال 1 تعرف العناصر المتناظرة المتطابقة بين أن المضلعين المجاورين متطابقان، بتعيين جميع العناصر المتناظرة المتطابقة. ثم اكتب عبارة التطابق. P Q R E D G F (18) J M 39 78° 40 50 52 39 52° 50° P /50° 78° 50 Q 40 L K ZPZG, ZQ=ZF, ZRZE, ZS ZD PQ = GE, QR = FE, RS = ED, SP = DG الزوايا : الأضلاع : تاريخ الرياضيات جوهان كارل فردريك جاوس (1777م - 1855م) قدم جاوس رمز التطابق ليبين أن طرفي المعادلة متساويان حتى ولو كانا مختلفين شكلا. وقد حقق إنجازات عديدة في الرياضيات والفيزياء تتضمن برهانا للنظرية الأساسية في الجبر وبما أن جميع العناصر المتناظرة للمضلعين متطابقة، فإنّ المضلع PQRS = المضلع GFED . تحقق من فهمك B W أداة الربط "إذا وفقط إذا التي وردت في تعريف المضلعات المتطابقة تعني أن كلا من العبارة الشرطية وعكسها صحیحتان؛ لذا إذا كان المضلعان متطابقين، فإن عناصرهما المتناظرة متطابقة. وإذا كانت العناصر المتناظرة متطابقة فإن المضلعين متطابقان. B 99° 32.1 38.4 45" 36° A 54 E 2y+x D (8y-5)% F مثال 2 تعيين العناصر المتناظرة المتطابقة في الشكل المجاور إذا كان ABC = ADFE ، ، فأوجد قيمة كل من x ZF = ZB العناصر المتناظرة متطابقة تعريف التطابق 2y-1 S R 24.5 x° T 78 V 24 الدرس - المثلثات المتطابقة الت29 Ministry of Education 2024-1446 عوض اجمع 5 إلى الطرفين اقسم الطرفين على 8 العناصر المتناظرة متطابقة تعريف التطابق عوض عوض بسط mZF=mZB 8y-5=99 8y = 104 y= 13 FE = BC FE = BC 2y + x = 38.4 2(13) + x = 38.4 26 + x = 38.4 إرشادات للدراسة استعمال عبارة التطابق يمكنك استعمال عبارة التطابق لمساعدتك على معرفة الأضلاع المتناظرة. AABC = ADFE BC=FE x = 12.4 تحقق من فهمك اطرح 26 من الطرفين (2) في الشكل المجاور إذا كان ARSV = ATVS، فأوجد قيمة كل من x

1A: بين أن المضلعين المجاورين متطابقان، بتعيين جميع العناصر المتناظرة المتطابقة، ثم اكتب عبارة التطابق


جوهان كارل فردريك جاوس
استعمال عبارة التطابق
إثبات تطابق المثلثات إن نظرية مجموع قياسات زوايا المثلث التي تعلمتها في الدرس 2-3 تقود إلى نظرية أخرى حول الزوايا في مثلثين. نظرية 3.3 نظرية الزاوية الثالثة التعبير اللفظي : إذا تطابقت زاويتان في مثلث مع زاويتين في مثلث آخر، مثال: فإن الزاوية الثالثة في المثلث الأول تطابق الزاوية الثالثة في المثلث الثاني إذا كانت: CK, BE LI فإن: ALL ستبرهن هذه النظرية في السؤال 17 L B K الربط مع الحياة استعمال بعض المهارات الأساسية عند طي مناديل المائدة يُضفي لمسة من مثال 3 من واقع الحياة استعمال نظرية الزاوية الثالثة تنظيم الحفلات قرّر منظمو حفلة مدرسية أن يطووا مناديل الطعام على صورة جيب مثلثي حتى يتمكنوا من وضع هدية بسيطة فيه. إذا كانت: °40 = NPQ = LRST, mZNPQ ، فأوجد mLSRT . بما أن NPQRST ، ولأن جميع الزوايا القائمة متطابقة (NQP = LRTS) ، فإنّ QNP = SRT بحسب نظرية الزاوية الثالثة؛ إذن mLQNP = mLSRT. mZQNP+mZNPQ = 90° mZQNP+40° = 90° mZQNP = 50 R الزاويتان الحادتان في المثلث القائم الزاوية متتامتان عوض W الجمال والأناقة على أي حفلة وكثير من هذه الطيات تأخذ شكل المثلث اطرح 40 من الطرفين وبالتعويض فإن : 50 = mZSRT = mZQNP. تحقق من فهمك (3) في الشكل أعلاه ، إذا كانت WNX = WRX، وكان WX منصفا لـ NXR ، وكان 49 = mWNX = 88, mZNXW ، فأوجد mZNWR. وفسّر إجابتك. مثال 4 إثبات تطابق مثلثين اكتب برهانا ذا عمودين. المعطيات DE = GE , DF = GF DE LG LDFE = ZGFE المطلوب: ADEF = AGEF البرهان إرشادات للدراسة خاصية الانعكاس عندما يشترك مثلثان 30 في ضلع، استعمل خاصية الانعكاس للتطابق؛ لتثبت أن الضلع المشترك يطابق نفسه. الفصل 3 المثلثات المتطابقة العبارات DE = GE, DF = GF (1 EF = EF (2 ZD ZG, ZDFE = ZGFE (3 LDEF = LGEF (4) ADEF AGEF (5 المبررات 1) معطيات F أضف إلى مطويتك E N 2) خاصية الانعكاس للتطابق (3) معطيات (4) نظرية الزاوية الثالثة (5) تعريف المضلعات المتطابقة وزارة التعليم Ministry of Education 2024-1446

استعمال بعض المهارات الاساسية عند طي المناديل العائدة يضفي لمسة من الجمال والأناقة على أي حفلة
تحقق من فهمك (4) اكتب برهانا ذا عمودين. المعطيات J = LP, JK = PM L ، JL = PL تنصف KM المطلوب : AJLK = APLM M L # P علاقة تطابق المثلثات علاقة انعكاس وتماثل وتعد كما في تطابق القطع المستقيمة والزوايا. النظرية 3.4 خصائص تطابق المثلثات خاصية الانعكاس للتطابق K أضف إلى تك مطويب B C E F G K AABC = AABC خاصية التماثل للتطابق إذا كان ABC = EFG ، فإن AEFG = ABC . خاصية التعدي للتطابق إذا كان ABC = EFG, EFG = AJKL ، فإن AABC = AJKL . ستبرهن عناصر هذه النظرية في الأسئلة 182021 1 تأكـ المثال 1 في كل من السؤالين الآتيين بيّن أن المضلعين متطابقان بتعيين جميع العناصر المتناظرة المتطابقة، ثم اكتب D A B E F (2 L S (2y-40)% R 3x 9 2x + 11 W Q M H L (y + (10) ° M X L 65A 51° N \(4x)° X R Z عبارة التطابق : S (1 المثال 2 في الشكلين المجاورين، إذا كان ALMN = AQRS فأوجد: Y (6 (3) قيمة . (4) قيمة . المثال 3 في كلُّ من السؤالين الآتيين، أوجد قيمة x، وفسّر إجابتك. (5 B G F (2x)° 80° A C H المثال 4 (7) برهان اكتب برهانا حرا. المعطيات WXZ = YXZ, XZW = LXZY, WX = YX, WZ = YZ الدرس - المثلثات المتطابقة الت31 ry of Educat 2024-1446 المطلوب : AWXZ = AYXZ

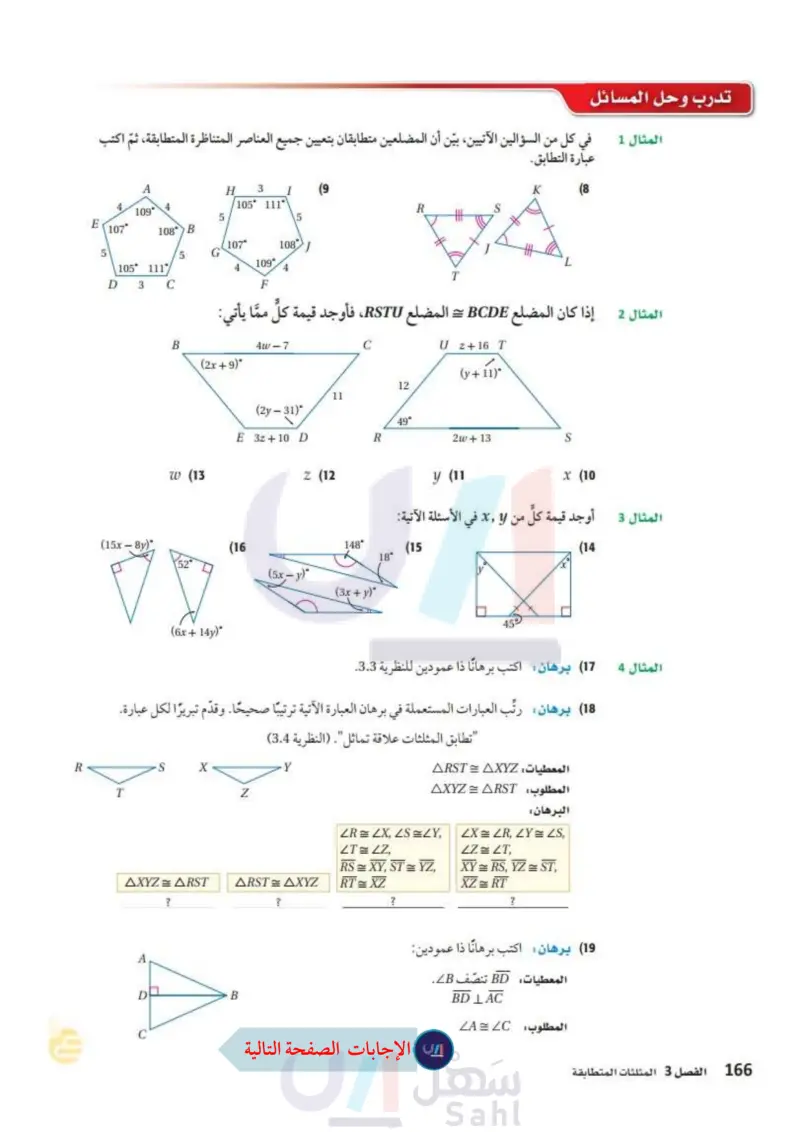
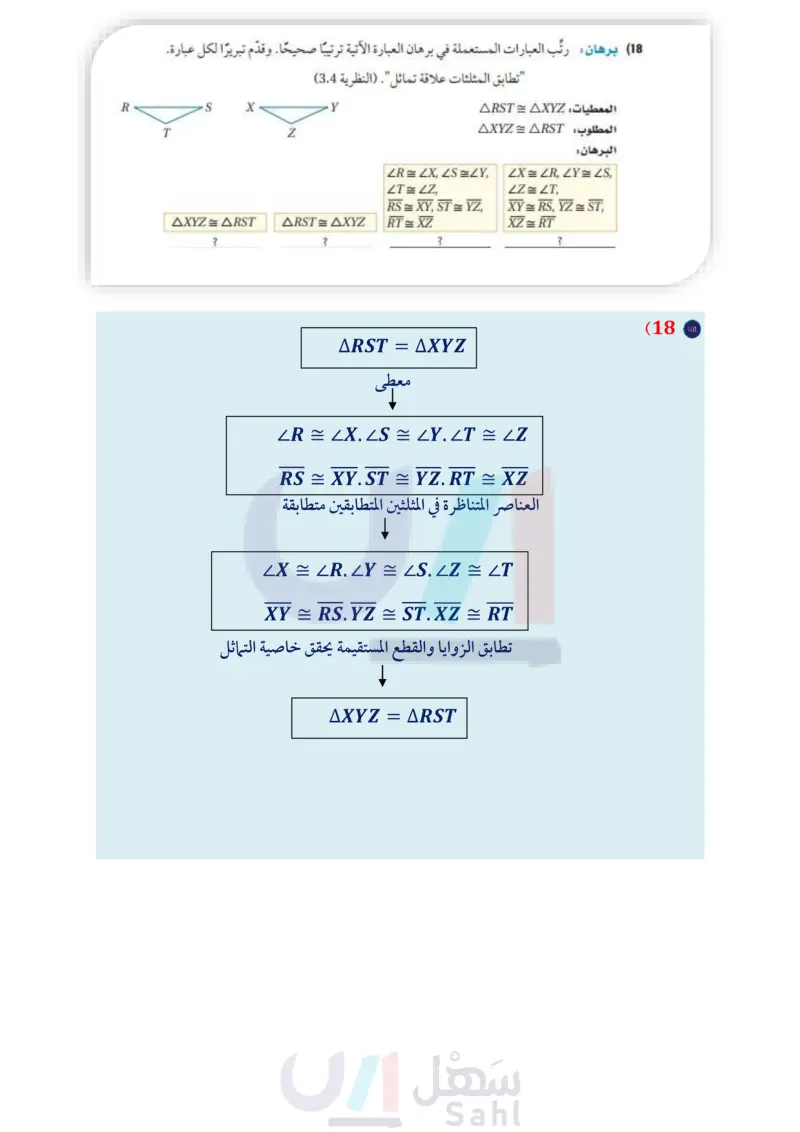
تدرب وحل المسائل في كل من السؤالين الآتيين، بيّن أن المضلعين متطابقان بتعيين جميع العناصر المتناظرة المتطابقة، ثم اكتب المثال 1 عبارة التطابق. H 3 I (9 4 105° 111° 109° E 107° 5 5 108° B 107° 108 J 5 5 G 109° 105° 111 4 4 D 3 C F T K (8 S إذا كان المضلع BCDE = المضلع RSTU، فأوجد قيمة كل مما يأتي: المثال 2 B (2x+9)° 4w-7 C U 2 + 16 T (y+11) 12 11 (2y-31)° 49° E 3z+10 D R 2w+13 S 20 (13 2 (12) y (11 x (10 أوجد قيمة كل من x في الأسئلة الآتية: المثال 3 (15x-8y) (16) 148° 18° (15 (14 (5x- 5x-y) (3x+y) (6x+14y)° 45° 17 برهان اكتب برهانا ذا عمودين للنظرية 3.3. المثال 4 18) برهان رتب العبارات المستعملة في برهان العبارة الآتية ترتيبًا صحيحًا. وقدم تبريرا لكل عبارة. "تطابق المثلثات علاقة تماثل". (النظرية (3.4) المعطيات: ARST = AXYZ المطلوب : AXYZ = ARST البرهان : R X T Z وزارة التعليم Ministry of Education 2024-1446 AXYZ = ARST ? ARST = AXYZ ? A D B ZR ZX, ZSZY, ZTZZ, RS = XY, ST = YZ, RT = XZ ? XER, YES, LZ = LT XY = RS, YZ = ST, XZ = RT ? (19) برهان اكتب برهانا ذا عمودين: المعطيات BD تنصف B. BD LAC المطلوب : LA C الفصل 3 المثلثات المتطابقة 32

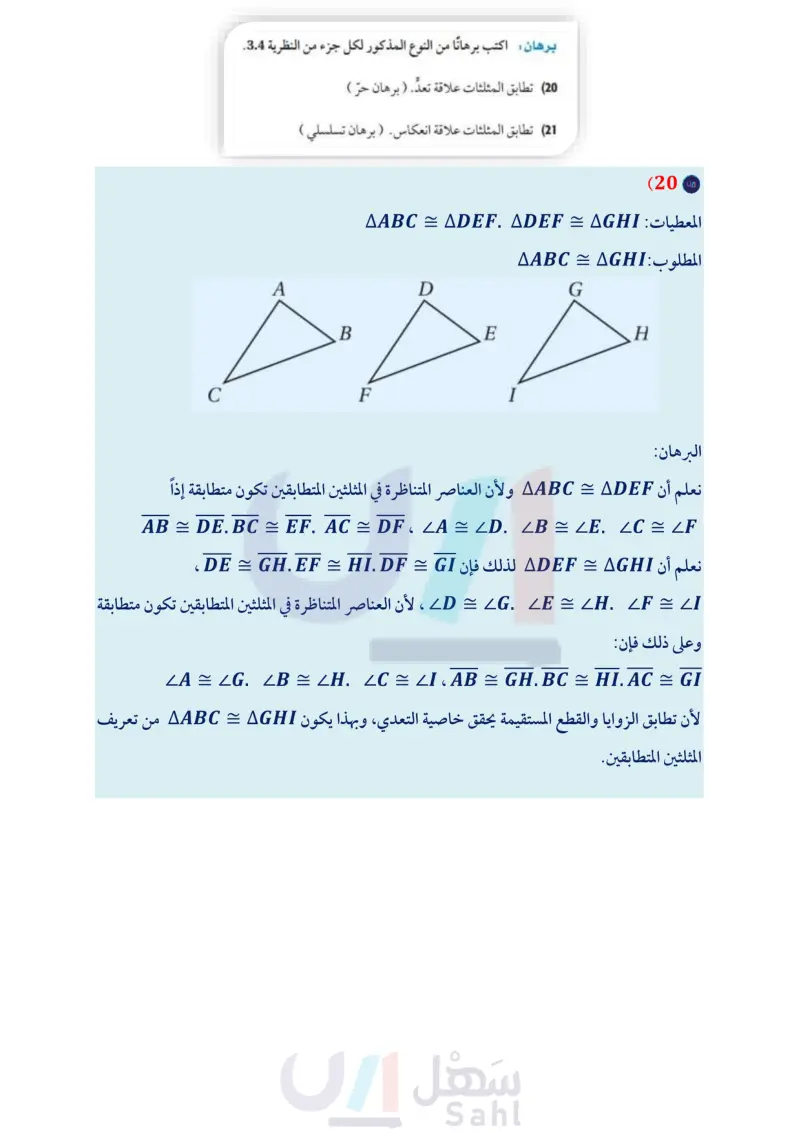
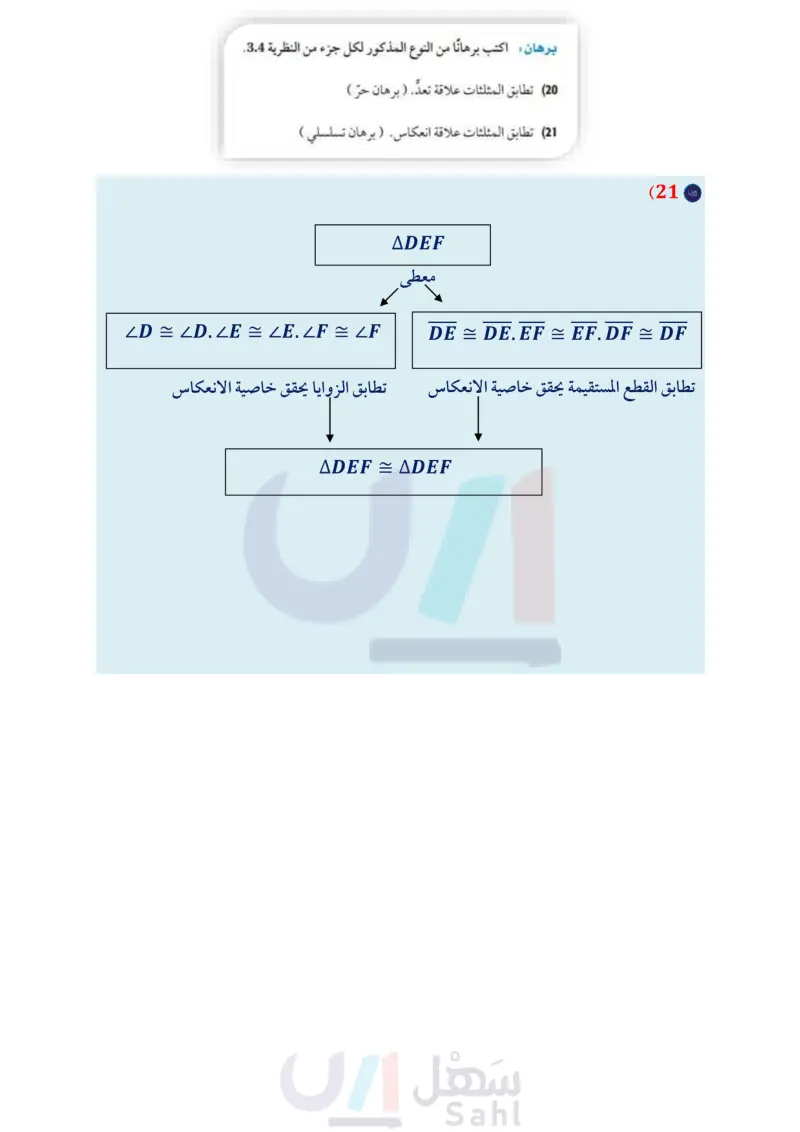
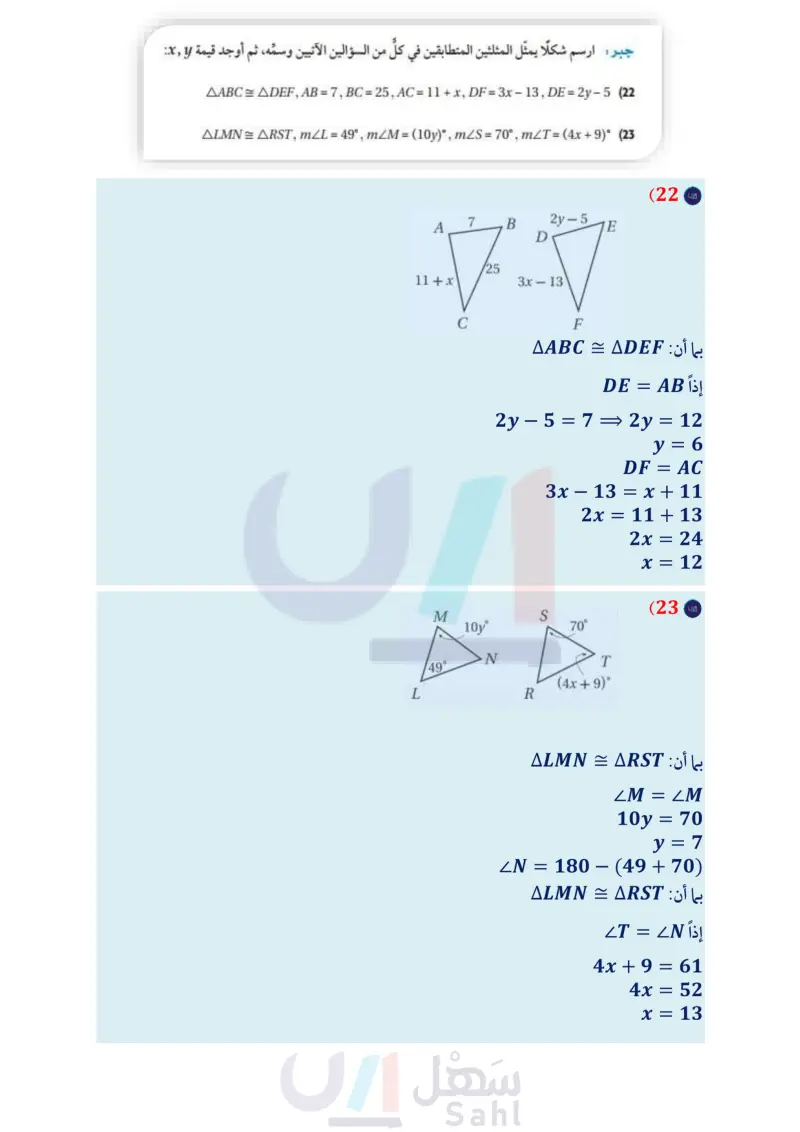
برهان اكتب برهانا من النوع المذكور لكل جزء من النظرية 3.4. (20) تطابق المثلثات علاقة تعد. (برهان حرّ ) (21) تطابق المثلثات علاقة انعكاس. (برهان تسلسلي ) جبر: ارسم شكلا يمثل المثلثين المتطابقين في كلٌّ من السؤالين الآتيين وسمه، ثم أوجد قيمة x: AABC = ADEF, AB - , BC = 25, AC = 11 + x, DF = 3x - 13, DE = 2y - 5 (22) ALMN = ARST, mL = 49°, mM = (10y), mLS = 70°, mLT = (4x + 9° (23) 24 رايات في مهرجان رياضي، كان سعيد مسؤولًا عن إحاطة منطقة مساحتها 2 ft 100 مخصصة لجلوس المعلقين والإعلاميين، فاستعمل حبلًا وثبت عليه رايات على شكل مثلثات متطابقة، كلّ منها متطابق الضلعين. إرشاد: 1ft = 12in 4 in. 6 in. B ) اكتب سبعة أزواج من القطع المستقيمة المتطابقة في الصورة. إذا كانت المنطقة التي حوطها سعيد بحبل الرايات مربعة الشكل، فكم سيكون طول الحبل ؟ ما عدد الرايات المثبتة بالحبل ؟ تمثيلات متعددة في هذه المسألة ستكتشف العلاقة بين مساحات المضلعات المتطابقة: لفظيا : اكتب عبارة شرطية تمثل العلاقة بين مساحتي مثلثين متطابقين. لفظيا : اكتب عكس عبارتك الشرطية. وهل العبارة العكسية صحيحة أم خطأ؟ وضح تبريرك. هندسيًا : ارسم - إن أمكن - مستطيلين لهما المساحة نفسها، ولكنهما غير متطابقين، وإذا كان ذلك غير ممكن فوضح السبب. d) هندسيا : ارسم - إن أمكن - مربعين لهما المساحة نفسها، ولكنهما غير متطابقين، وإذا كان ذلك غير ممكن فوضح السبب. الدرس - المثلثات المتطابقة الـ 33 Ministry of Education 2024-1446 (25

برهان اكتب برهانا من النوع المذكور لكل جزء من النظرية 3.4. (20) تطابق المثلثات علاقة تعد. (برهان حرّ ) (21) تطابق المثلثات علاقة انعكاس. (برهان تسلسلي ) جبر: ارسم شكلا يمثل المثلثين المتطابقين في كلٌّ من السؤالين الآتيين وسمه، ثم أوجد قيمة x: AABC = ADEF, AB - , BC = 25, AC = 11 + x, DF = 3x - 13, DE = 2y - 5 (22) ALMN = ARST, mL = 49°, mM = (10y), mLS = 70°, mLT = (4x + 9° (23) 24 رايات في مهرجان رياضي، كان سعيد مسؤولًا عن إحاطة منطقة مساحتها 2 ft 100 مخصصة لجلوس المعلقين والإعلاميين، فاستعمل حبلًا وثبت عليه رايات على شكل مثلثات متطابقة، كلّ منها متطابق الضلعين. إرشاد: 1ft = 12in 4 in. 6 in. B ) اكتب سبعة أزواج من القطع المستقيمة المتطابقة في الصورة. إذا كانت المنطقة التي حوطها سعيد بحبل الرايات مربعة الشكل، فكم سيكون طول الحبل ؟ ما عدد الرايات المثبتة بالحبل ؟ تمثيلات متعددة في هذه المسألة ستكتشف العلاقة بين مساحات المضلعات المتطابقة: لفظيا : اكتب عبارة شرطية تمثل العلاقة بين مساحتي مثلثين متطابقين. لفظيا : اكتب عكس عبارتك الشرطية. وهل العبارة العكسية صحيحة أم خطأ؟ وضح تبريرك. هندسيًا : ارسم - إن أمكن - مستطيلين لهما المساحة نفسها، ولكنهما غير متطابقين، وإذا كان ذلك غير ممكن فوضح السبب. d) هندسيا : ارسم - إن أمكن - مربعين لهما المساحة نفسها، ولكنهما غير متطابقين، وإذا كان ذلك غير ممكن فوضح السبب. الدرس - المثلثات المتطابقة الـ 33 Ministry of Education 2024-1446 (25

2 74' 15" 3 مراجعة تراكمية في الشكل المجاور أوجد كلًا من القياسات الآتية: (الدرس (2-3) mz2 (34 m21 (35 mZ3 (36 (37) هندسة إحداثية: أوجد أطوال أضلاع JKL) الذي رؤوسه هي (--) ,0 ,15)K ,(10 ,7-) ، وصنفه وفقا لأطوال أضلاعه. (الدرس 1-3) حدد ما إذا كانت كل عبارة مما يأتي صحيحةً دائمًا أو أحيانًا أو ليست صحيحة أبدًا: (مهارة سابقة) (38) تكون الزاويتان المتجاورتان على خط مستقيم متكاملتين. (39) إذا كانت الزاويتان متكاملتين فإن إحداهما تكون منفرجة. MR. الدرس - المثلثات المتطابقة الـ 35 Ministry of Education 2024-1446 N P SQ المبررات (a) معطيات ؟ ؟ تعريف القطع المستقيمة المتطابقة استعد للدرس اللاحق 40) انقل البرهان الآتي وأكمله : المعطيات MN = PQ, PQ = RS المطلوب : MN = RS العبارات البرهان : (b MN PQ, PQ = RS (b MN RS (d