حل المعادلات والمتباينات الأسية - رياضيات1-3 - ثالث ثانوي

رابط الدرس الرقمي حل المعادلات والمتباينات الأسية www.ien.edu.sa Solving Exponential Equations and Inequalities وزارة التعليم Ministry of Education 2024-1446 2-2 فيما سبق: درست تمثيل الدوال الأسية بيانيا. (الدرس 1-2) والآن : أحل معادلات أسية. أحل متباينات أسية أحل مسائل تتضمن نموا أسيا واضمحلالا أسيًا. المفردات: المعادلة الأسية exponential equation الربح المركب compound interest المتباينة الأسية exponential inequality لماذا؟ تتزايد اشتراكات مواقع الإنترنت بطريقة سريعة، فتأخذ شكل دالة أسية. فإذا كان عدد الاشتراكات في أحد المواقع يُعطى بالمعادلة y = 2.2(1.37) x حيث x عدد السنوات منذ عام 1435هـ ، و لا عدد المشتركين بالملايين فيمكنك استعمال المعادلة * (1.37)2.2 = y لتحديد عدد المشتركين في سنة معينة، أو تحديد السنة التي يكون فيها عدد المشتركين عند مستوى معين. حل المعادلات الأسية تظهر المتغيرات في المعادلة الأسية في موقع الأسس. مفهوم أساسي خاصية المساواة للدوال الأسية التعبير اللفظي: إذا كان 01 b، فإن b = by إذا وفقط إذا كان x = y. إذا كان 35 = 3 ، فإن 5 = x . و إذا كان 5 = x ، فإن 35 = x 3 . مثال : يمكنك استعمال خاصية المساواة للدوال الأسية لحل معادلات أسية. مثال 1 حُلّ كل معادلة مما يأتي: حل المعادلات الأسية 55x = 125x + 2 (1B المعادلة الأصلية 8 = 23 خاصية قوة القوة خاصية المساواة للدوال الأسية المعادلة الأصلية 9 = 32 خاصية قوة القوة خاصية المساواة للدوال الأسية بطرح 4x من كلا الطرفين بقسمة كلا الطرفين على 2 2x = 83 (a 2x = 83 2x = (23)3 2x = 29 x = 9 92x-136x (b 92x - 1 = 36x (32) 2x - 1 = 36x 34x - 2 = 36x 4x-2=6x -2 = 2x -1 = x تحقق من فهمك 421 - 1 = 641A 42n-1 : الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 90

يمكنك استعمال معلومات عن النمو أو الاضمحلال لكتابة دالة أسية. مثال 2 من واقع الحياة كتابة دالة أسية علوم بدأ سلطان تجربة مخبرية بـ 7500 خلية بكتيرية. وبعد أربع ساعات أصبح عدد الخلايا البكتيرية 23000 خلية. a اكتب دالة أسية على الصورة * y = ab تمثل عدد الخلايا البكتيرية بعد x ساعة إذا استمر تغير عدد الخلايا البكتيرية بالمعدل نفسه مقربًا الناتج إلى أقرب ثلاث منازل عشرية. في بداية التجربة كان الزمن (x) صفر ساعة ، وعدد الخلايا (y) يساوي 7500 خلية بكتيرية، لذا عوّض هذه القيم لإيجاد المقطع y أو قيمة a . y = abx 7500 = a b 0 7500 = a وعندما 4 = x، يصبح . الدالة الأس دسية بالتعويض عن x بالعدد 0 ، وعن 4 بالعدد 7500 60 = 1 عدد الخلايا البكتيرية 23000 ، عوّض هذه القيم في الدالة الأسية لتحديد قيمة b. 23000 = 7500.64 3.067b4 √3.067 ≈ b 1.323 ~ b بالتعويض عن x بالعدد 4، وعن y بالعدد 23000، وعن a بالعدد 7500 بقسمة كلا الطرفين على 7500 بإيجاد الجذر الرابع للطرفين باستعمال الحاسبة الدالة التي تمثل عدد الخلايا البكتيرية هي (1.323)7500 = y . ما العدد المتوقع للخلايا البكتيرية بعد 12 ساعة؟ أوراق RE-US RECYCLE بلاستيك RE-USE RECYCLE الربط مع الحياة EDUCE زجاج RE-USE 63 RECYCLE قبل إعادة تدوير البلاستيك يتم غسله بمادة الصودا الكاوية المضاف إليها الماء الساخن. ولا ينصح باستعمال العبوات المعاد تدويرها للمواد الغذائية. y = 7500(1.323)* = 7500(1.323)12 ≈ 215664 المعادلة التي تمثل عدد الخلايا البكتيرية بالتعويض عن x بالعدد 12 باستعمال الحاسبة سيكون هنالك 215664 خلية بكتيرية تقريبًا بعد 12 ساعة. تحقق من فهمك 2 إعادة تصنيع : أنتج مصنع 3.2 ملايين عبوة بلاستيكية عام 1436هـ ، وفي عام 1440 هـ أنتج 420000 عبوة بإعادة تصنيع العبوات التي أنتجها عام 1436هـ. 2 مفترضًا أن إعادة التصنيع استمرت بالمعدل نفسه اكتب دالة أسية على الصورة * y = ab تمثل عدد العبوات المعاد تصنيعها ل بعد x سنة مقربًا الناتج إلى أقرب منزلتين عشريتين. (2B كم تتوقع أن يكون عدد العبوات المُعادة التصنيع عام 1481هـ ؟ تستعمل الدوال الأسية في مسائل تتضمن الربح المركب ؛ وهو الربح الذي يحسب المبلغ المستثمر (رأس المال) مضافًا إليه أي أرباح سابقة، وليس فقط عن رأس المال كما هو في الربح البسيط . مفهوم أساسي الربح المركب يمكنك حساب الربح المركب باستعمال الصيغة A = P(1 + ) " nt n حيث A المبلغ الكلي بعد t سنة، P المبلغ الأصلي الذي تم استثماره أو رأس المال ، r معدل الربح السنوي المتوقع، 1 عدد مرات إضافة الأرباح إلى رأس المال في السنة. وزارة التعليم الدرس 2-2 حل المعادلات والمتباينات الأسية of 91 2024-1446

مثال 3 الربح المركب تنبيه نسب مئوية : تذكر تحويل جميع النسب المئوية إلى كسور عشرية، مثل : 0.042 = %4.2 مال استثمر حمد مبلغ 25000 ريال في مشروع تجاري متوقعًا ربحًا سنويًّا نسبته %4.2 ، بحيث تُضاف الأرباح إلى رأس المال كل شهر . ما المبلغ الكلي المتوقع بعد 15 سنة مقربًا إلى أقرب منزلتين عشريتين؟ افهم : أوجد المبلغ الكلي المتوقع بعد 15 سنة. خطط بما أنه تتم إضافة الأرباح إلى رأس المال، إذن استعمل صيغة الربح المركب. : تنبيه! تقريب الأعداد : يمكنك تقريب الأعداد الظاهرة على الشاشة، بحيث تظهر على الرسم بالشكل المناسب وذلك بالضغط على مفتاح on 5 الإعدادات ثم اختيار 2: اعدادات المستند تحقق P = 25000, r = = 0.042, n = r\nt A = P(1 + 7/7) "* n = 25000 1 + 25000(1 ≈ 46888.66 12, t = 15 0.042 12.15 12 قل المعادلة المناظرة بيانيا صيغة الربح المركب P = 25000, r = 0.042, n = 12, t = 15 f(x) = 25000(1.0035)12x ، ثم أوجد قيمة y عندما = x 6 15 على الرسم بالضغط على مفتاح. واختيار 8 : الهندسة ومنها واختيار التقريب المناسب، وستظهر الأعداد اد بحسب عدد المنازل المطلوبة. menu ثم اختر واختر منها 1 : النقاط والمستقيمات 2 نقطة على المستقيم ثم اضغط على الرسم البياني لتحدد نقطة يظهر الزوج المرتب الذي يمثلها . اضغط esc ثم حدد الإحداثي x للنقطة واكتب 15، سيظهر الإحداثي y المقابل 46888.66 إذن الإجابة صحيحة. تحقق من فهمك باستعمال الحاسبة 18 区 192 1.3 1.2 1.1 $53000 y (15,46888.66) f1(x)=25000 (1.0035) 12. x (3) استثمر علي مبلغ 100000 ريال في مشروع تجاري متوقعًا ربحًا سنويًا نسبته 12 ، بحيث تُضاف الأرباح إلى رأس المال مرتين شهريا ما المبلغ الكلي المتوقع بعد 5 سنواتٍ مقربًا الناتج إلى أقرب منزلتين عشريتين؟ حل المتباينات الأسية : المتباينة الأسية هى متباينة تتضمن عبارة أسية أو أكثر. مفهوم أساسي خاصية التباين لدالة النمو التعبير اللفظي : إذا كان 1 b ، فإن b> by إذا وفقط إذا كان x > y مثال: إذا كان 26 < 2 ، فإن 6 < x ، و إذا كان ؛ 6 < x ، فإن 26 < 2 . تتحقق هذه الخاصية أيضًا مع رمز التباين < مفهوم أساسي خاصية التباين لدالة الاضمحلال x مثال: > التعبير اللفظي : إذا كان 1 > > 0 ، فإن b> by إذا وفقط إذا كان x < y إذا كان (1) < ) ، فإن 5 > x ، وإذا كان ؛ 5 > x ، فإن (1) < (1) . X > تتحقق هذه الخاصية أيضًا مع رمز التباين < مثال 4 حل المتباينات الأسية إرشادات للدراسة دالتا النمو والاضحلال الأسي: لاحظ أن خاصية التباين لدالة النمو تبين أن هذه الدالة متزايدة على مجالها وأن خاصية التباين لدالة الاضمحلال تبين أن هذه الدالة متناقصة على مجالها. 162x-3 < 8 (24)2x-3 <23 28x1223 8x - 12 < 3 8x < 15 15 8 x< حُلّ المتباينة 8 > 3-162x المتباينة الأصلية 16 = 24,8=23 خاصية قوة القوة خاصية التباين لدالة النمو بجمع 12 للطرفين بقسمة الطرفين على 8 92 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية وزارة التعليم Ministry of Education 2024-1446

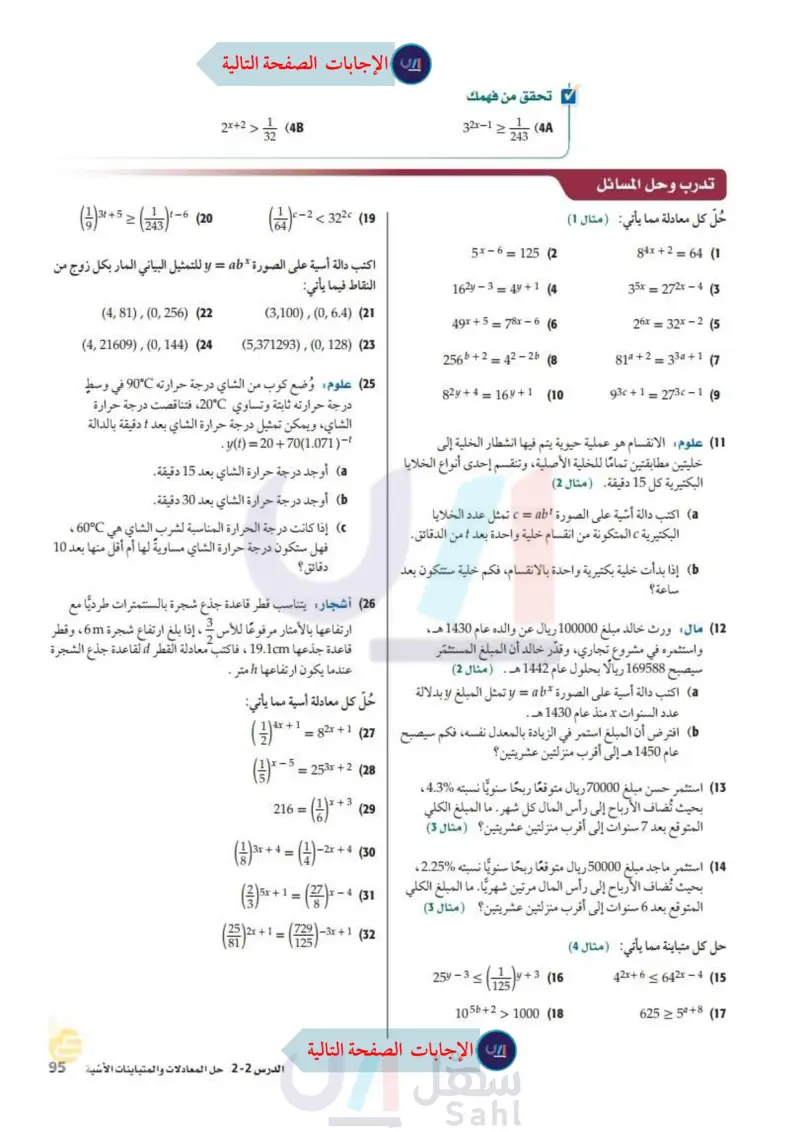
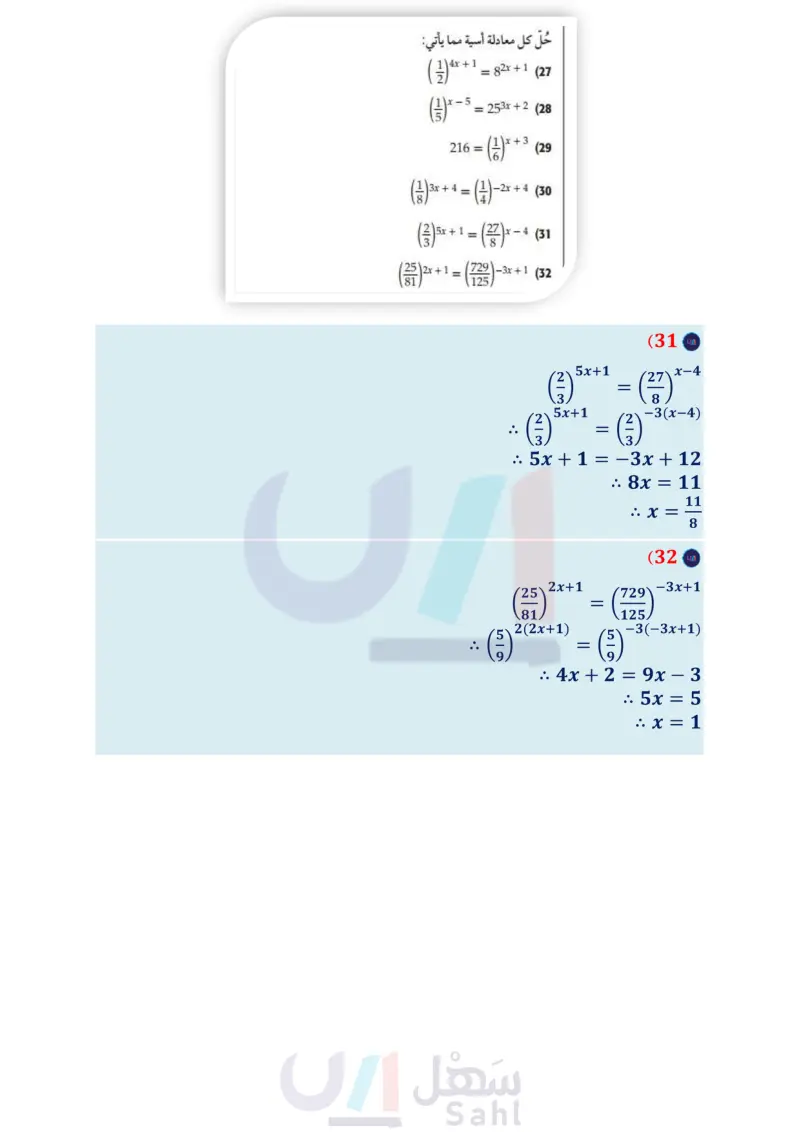
2x+2> 18 (4B 32 تحقق من فهمك 32x-1 > 1 243 (4A تدرب وحل المسائل (1) ³+ + 5 31 3t+5 1 > (243) -6 (20 64 (114) c-2 -2322c (19 حلّ كل معادلة مما يأتي: (مثال (1) 51-6 = 125 (2 84x + 2 = 64 (1 اكتب دالة أسية على الصورة * y = ab للتمثيل البياني المار بكل زوج من النقاط فيما يأتي: 1624 - 3 = 40 + 1 (4) 4y+1 (4,81), (0,256) (22 (4, 21609), (0, 144) (24 (3,100), (0,6.4) (21 (5,371293), (0, 128) (23 78x-6 (6 49x+578x 6 256b+2 42-2b = 35x = 272x - 4 (3) 26x=32x-2 (5 81a233a+1 (7 (8 82y+4= = 16y+1 (10 93 + 1 = 2730 - 1 273c-1 (9 (11) علوم الانقسام هو عملية حيوية يتم فيها انشطار الخلية إلى خليتين مطابقتين تمامًا للخلية الأصلية، وتنقسم إحدى أنواع الخلايا البكتيرية كل 15 دقيقة. ( مثال (2) a اكتب دالة أسية على الصورة c = ab تمثل عدد الخلايا البكتيرية ، المتكونة من انقسام خلية واحدة بعد t من الدقائق. إذا بدأت خلية بكتيرية واحدة بالانقسام، فكم خلية ستتكون بعد ساعة؟ (12) مال ورث خالد مبلغ 100000 ريال عن والده عام 1430هـ ، واستثمره في مشروع تجاري، وقدّر خالد أن المبلغ المستثمر 169588 ريالًا بحلول عام 1442هـ . (مثال (2) سيصبح (25) علوم وضع كوب من الشاي درجة حرارته 90°C في وسط درجة حرارته ثابتة وتساوي 20°C ، فتناقصت درجة حرارة الشاي، ويمكن تمثيل درجة حرارة الشاي بعد t دقيقة بالدالة . y(t)=20+70(1.071)-t a أوجد درجة حرارة الشاي بعد 15 دقيقة. أوجد درجة حرارة الشاي بعد 30 دقيقة. €60°C إذا كانت درجة الحرارة المناسبة لشرب الشاي هي فهل ستكون درجة حرارة الشاي مساويةً لها أم أقل منها بعد 10 دقائق؟ (26) أشجار يتناسب قطر قاعدة جذع شجرة بالسنتمترات طرديا مع ارتفاعها بالأمتار مرفوعًا للأس 3 ، إذا بلغ ارتفاع شجرة 6m، وقطر قاعدة جذعها 19.1cm ، فاكتب معادلة القطر d لقاعدة جذع الشجرة عندما يكون ارتفاعها h متر اكتب دالة أسية على الصورة * y = ab تمثل المبلغ y بدلالة حُلّ كل معادلة أسية مما يأتي: . عدد السنوات x منذ عام 1430هـ افترض أن المبلغ استمر في الزيادة بالمعدل نفسه، فكم سيصبح عام 1450 هـ إلى أقرب منزلتين عشريتين؟ (13) استثمر حسن مبلغ 70000 ريال متوقعًا ربحًا سنويًّا نسبته %4.3 ، بحيث تُضاف الأرباح إلى رأس المال كل شهر. ما المبلغ الكلي المتوقع بعد 7 سنوات إلى أقرب منزلتين عشريتين؟ (مثال (3) (14) استثمر ماجد مبلغ 50000 ريال متوقعًا ربحًا سنويًّا نسبته %2.25 ، بحيث تُضاف الأرباح إلى رأس المال مرتين شهريا. ما المبلغ الكلي المتوقع بعد 6 سنوات إلى أقرب منزلتين عشريتين؟ (مثال (3) حل كل متباينة مما يأتي: (مثال (4) (3) 3 - 5 = ( 3 ) 4x + 1 = 82x + 1 (27 253x + 2 (28 1x + 3 216 = (1) 3x + 4 5x+1 = = (41) 27 - 2x + 4 (2) 8 '729 -3x + 1 (29 (30 X (31 (32 = 125 23 • ( 252x + 1 81 2 وزارة التعليم الدرس 2- حل المعادلات والمتباينات الأسية M93 of 2024-1446 254-3 (25) + (16 105b+2>1000 (18 42x+ 6 = 642x - 4 (15 6255a+8 (17

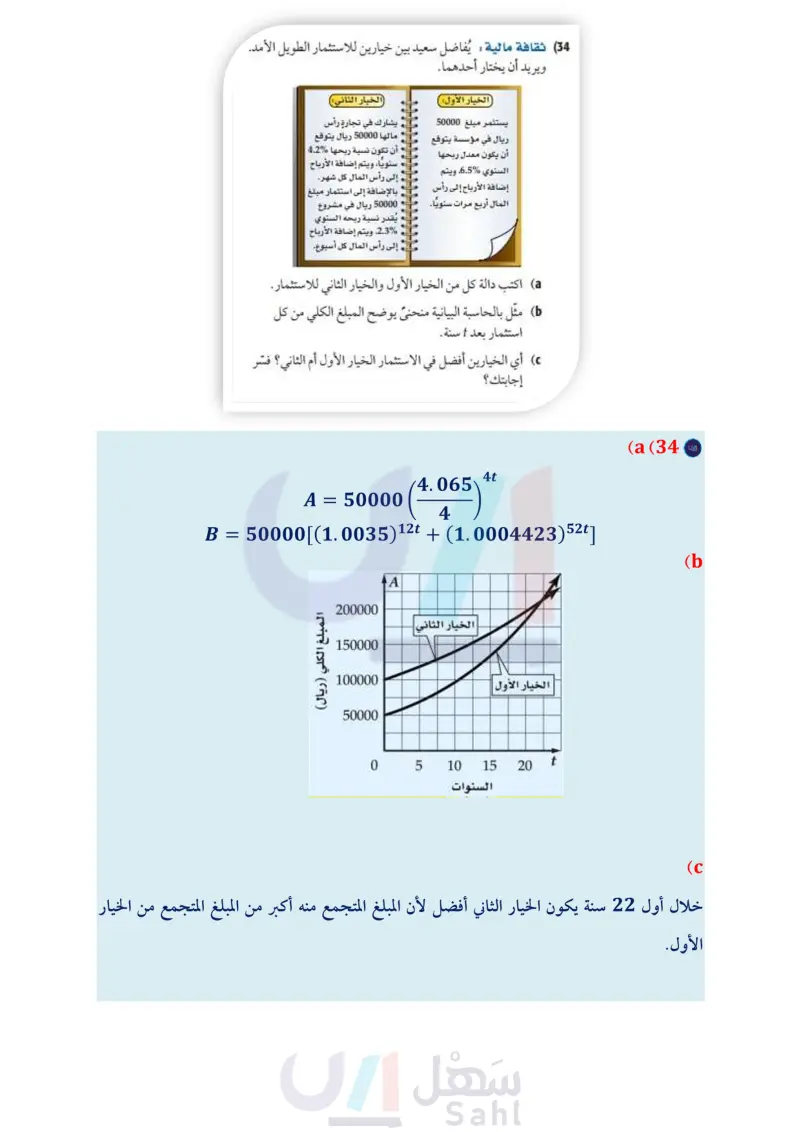
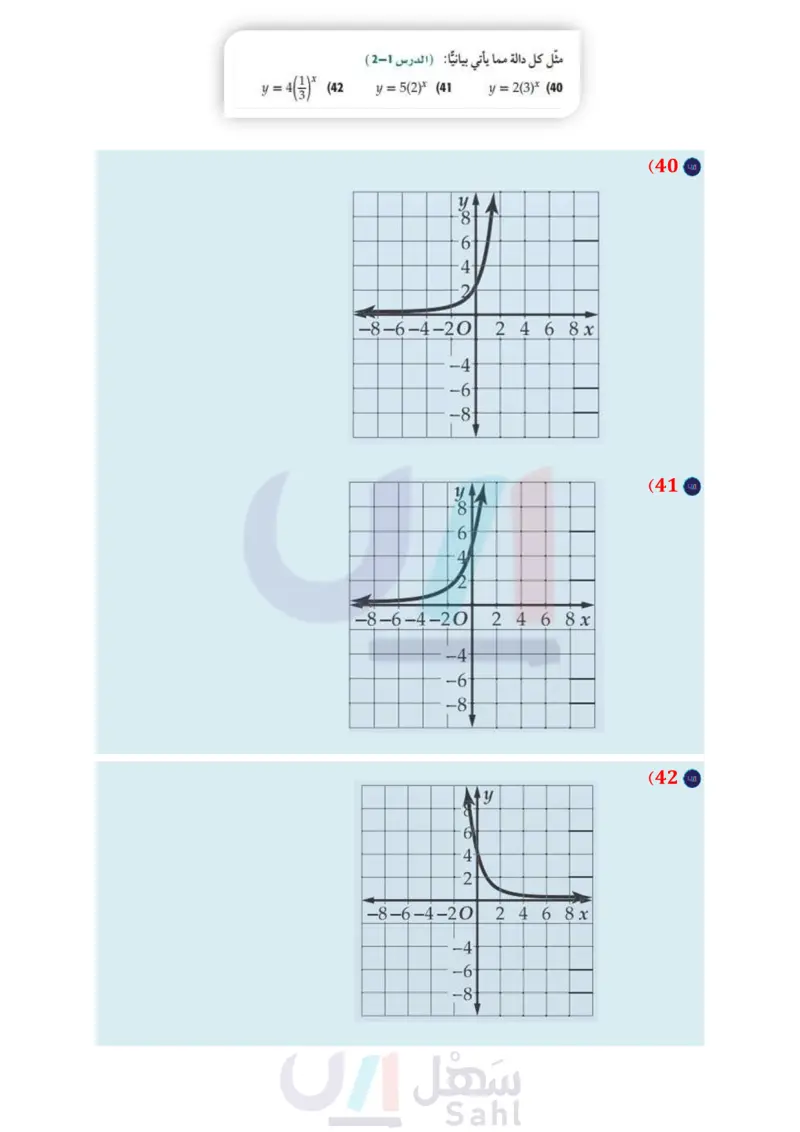
(33) سكان بلغ عدد سكان العالم عام 1950م ، 2.556 مليار نسمة، وبحلول عام 1980م أصبح 4.458 مليارات نسمة. b) مسائل مهارات التفكير العليا (36) تحد : حُلّ المعادلة الأسية 4 = 1618 + 1618 + 1618 + 1618. اكتب دالة أسية على صورة y = ab x يمكن أن تمثل تزايد عدد (37) مسألة مفتوحة : اكتب معادلة أسية يكون حلها 2 = x . سكان العالم من عام 1950م إلى عام 1980م بالمليار ، حيث x عدد السنوات منذ عام 1950م (قرّب قيمة b إلى أقرب جزء من (38 برهان أثبت أن 1 + 272x . 81 x + 1 = 32x + 2 . 4x . عشرة آلاف) افترض أن تزايد عدد السكان استمر بالمعدل نفسه، فقدّر عدد سكان العالم عام 2000 . إذا كان عدد سكان العالم عام 2000م هو 6.08 مليارات نسمة تقريبًا، فقارن بين تقديرك والعدد الحقيقي للسكان. d استعمل الدالة التي توصلت إليها في فرع a لتقدير عدد سكان العالم عام 2020م. ما دقة تقديرك؟ وضح إجابتك. (39) تبرير حدد ما إذا كانت العبارة الآتية صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. وضح إجابتك (820x) - < 2 لجميع قيم x . مراجعة تراكمية (34) ثقافة مالية : يُفاضل سعيد بين خيارين للاستثمار الطويل الأمد، مثل كل دالة مما يأتي بيانيا (الدرس 1-2 ) ويريد أن يختار أحدهما. الخيار الأول: يستثمر مبلغ 50000 ريال في مؤسسة يتوقع أن يكون معدل ربحها السنوي 6.5%، ويتم إضافة الأرباح إلى رأس المال أربع مرات سنويا. الخيار الثاني يشارك في تجارة رأس مالها 50000 ريال يتوقع أن تكون نسبة ربحها %4.2 سنويا، ويتم إضافة الأرباح إلى رأس المال كل شهر. بالإضافة إلى استثمار مبلغ 50000 ريال في مشروع يقدر نسبة ربحه السنوي 2.3%، ويتم إضافة الأرباح إلى رأس المال كل أسبوع. اكتب دالة كل من الخيار الأول والخيار الثاني للاستثمار. ( مثل بالحاسبة البيانية منحنى يوضح المبلغ الكلي من كل استثمار بعد أ سنة. أي الخيارين أفضل في الاستثمار الخيار الأول أم الثاني؟ فسّر إجابتك ؟ (35) تمثيلات متعددة ستستكشف في هذا التمرين الزيادة : المتسارعة في الدوال الأسية . قصَّ ورقة إلى نصفين، وضع بعضهما فوق بعض، ثم قصَّهما معًا إلى نصفين وضع بعضهما فوق بعض، وكرّر هذه العملية عدة مرات. (a حسيًّا : عُدّ قطع الورق الناتجة بعد القص الأول، ثم بعد القص الثاني والثالث والرابع جدوليًّا دون نتائجك في جدول. رمزيا: استعمل النمط في الجدول لكتابة معادلة تمثل عدد قطع الورق بعد القص x مرة. d تحليليًا يُقدر سُمك الورقة الاعتيادية بنحو 0.003in ، اكتب معادلة تمثل سُمك رزمة الورق بعد قصها x مرة. e تحليليا : ما سُمك رزمة من الورق بعد قصها 30 مرة؟ Y: = 4(13) * (42 y = 5(2)* (41 y = 2(3)* (40 حُلّ كل معادلة مما يأتي: (مهارة سابقة ) Vx + 5 – 3 = 0 (43 12x - 1 = 2 (45) − V3 - 5 - 3 = 4 (44 (5x+75 +3= 5 (46 1 (7x1)3+4=2 (48 (3x – 2) 5 + 6 = 5 (47 أوجد ( x ) لكل زوج من الدوال الآتية: (الدرس 6-1 ) (x) = 2x - 1 (49) g(x)=3x+4 O h(x) = x +4 (50 g(x) = |x| (51) أوجد الدالة العكسية للدالة: 1 + f(x) = 2x (الدرس 17 ) تدريب على اختبار (52) ما قيمة x التي تحقق المعادلة 8 = 7 + 1-7x ؟ -1 A 0 B 1C 2 D (53) إذا كانت f(x) = 5x ، فما قيمة [(1-)f[f؟ -25 A -5 B 5 C 25 D 94 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية وزارة التعليم Ministry of Education 2024-1446