متباينة المثلث - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
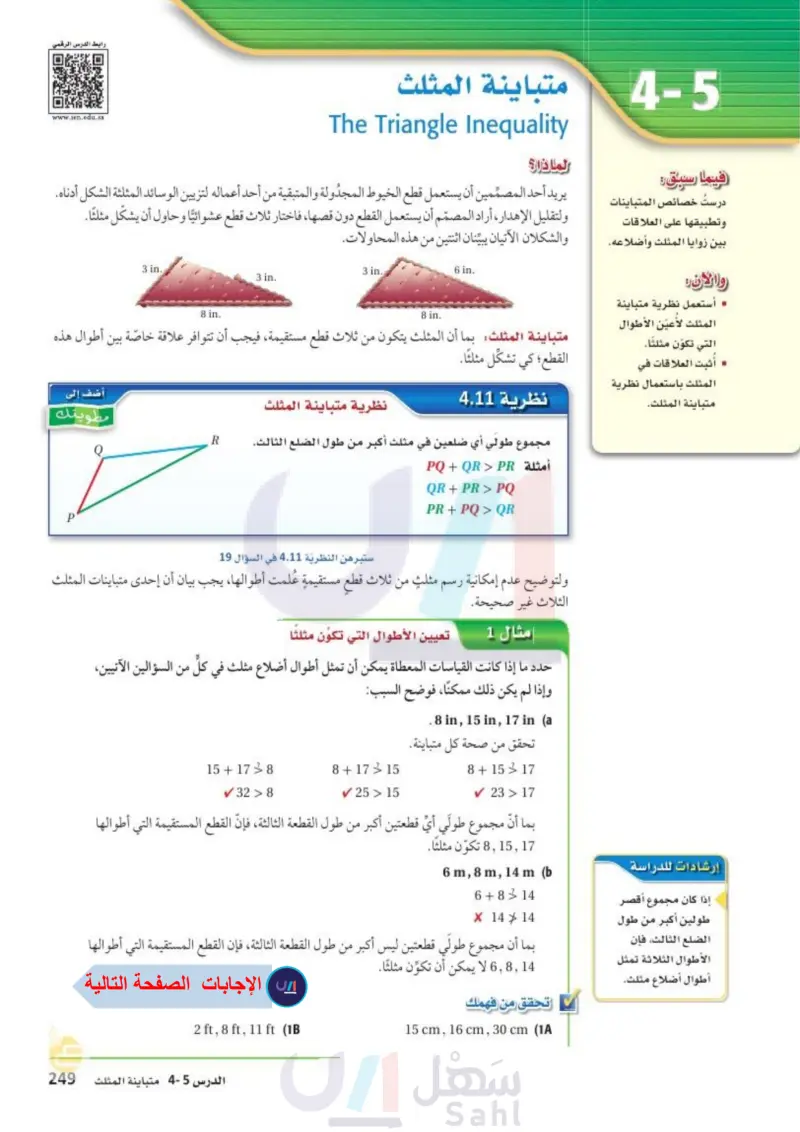
www.ien.edu.sa متباينة المثلث The Triangle Inequality الماذا؟ 4-5 فيما سبق درست خصائص المتباينات يريد أحد المصممين أن يستعمل قطع الخيوط المجدولة والمتبقية من أحد أعماله لتزيين الوسائد المثلثة الشكل أدناه. وتطبيقها على العلاقات ولتقليل الإهدار ، أراد المصمم أن يستعمل القطع دون قصها، فاختار ثلاث قطع عشوائيا وحاول أن يشكل مثلثا. بين زوايا المثلث وأضلاعه والشكلان الآتيان يبينان اثنتين من هذه المحاولات. 3 in.. 3 in. 3 in. 6 in. والان أستعمل نظرية متباينة 8 in. 8 in. المثلث لأعين الأطوال متباينة المثلث بما أن المثلث يتكون من ثلاث قطع مستقيمة، فيجب أن تتوافر علاقة خاصة بين أطوال هذه التي تكون مثلثا. أثبت العلاقات في المثلث باستعمال نظرية متباينة المثلث. القطع؛ كي تشكل مثلثا. نظرية 4.11 نظرية متباينة المثلث مجموع طولي أي ضلعين في مثلث أكبر من طول الضلع الثالث. أمثلة PQ + QR > PR R أضف إلى مطويتك QR + PR > PQ PR + PQ > QR ستبرهن النظرية 4.11 في السؤال 19 ولتوضيح عدم إمكانية رسم مثلث من ثلاث قطع مستقيمةٍ عُلمت أطوالها، يجب بيان أن إحدى متباينات المثلث الثلاث غير صحيحة. مثال 1 تعيين الأطوال التي تكون مثلثا حدد ما إذا كانت القياسات المعطاة يمكن أن تمثل أطوال أضلاع مثلث في كل من السؤالين الآتيين، وإذا لم يكن ذلك ممكنا، فوضح السبب: 15+178 8+ 1715 ✓ 32 8 25 > 15 .8 in, 15 in, 17 in (a تحقق من صحة كل متباينة. 8+ 1517 V 23 > 17 بما أن مجموع طولي أي قطعتين أكبر من طول القطعة الثالثة، فإنّ القطع المستقيمة التي أطوالها تكون مثلثا . 6 m, 8 m, 14 m (b 6+814 X 147 14 إرشادات للدراسة إذا كان مجموع أقصر طولين أكبر من طول الضلع الثالث، فإن الأطوال الثلاثة تمثل أطوال أضلاع مثلث. بما أن مجموع طولي قطعتين ليس أكبر من طول القطعة الثالثة، فإن القطع المستقيمة التي أطوالها 6,814 لا يمكن أن تكون مثلثا. تحقق من فهمك 2 ft, 8 ft, 11 ft (1B الدرس 5-4 متباينة المثلثة ال115 Ministry of E 2024-1446 15 cm, 16 cm, 30 cm (1A "

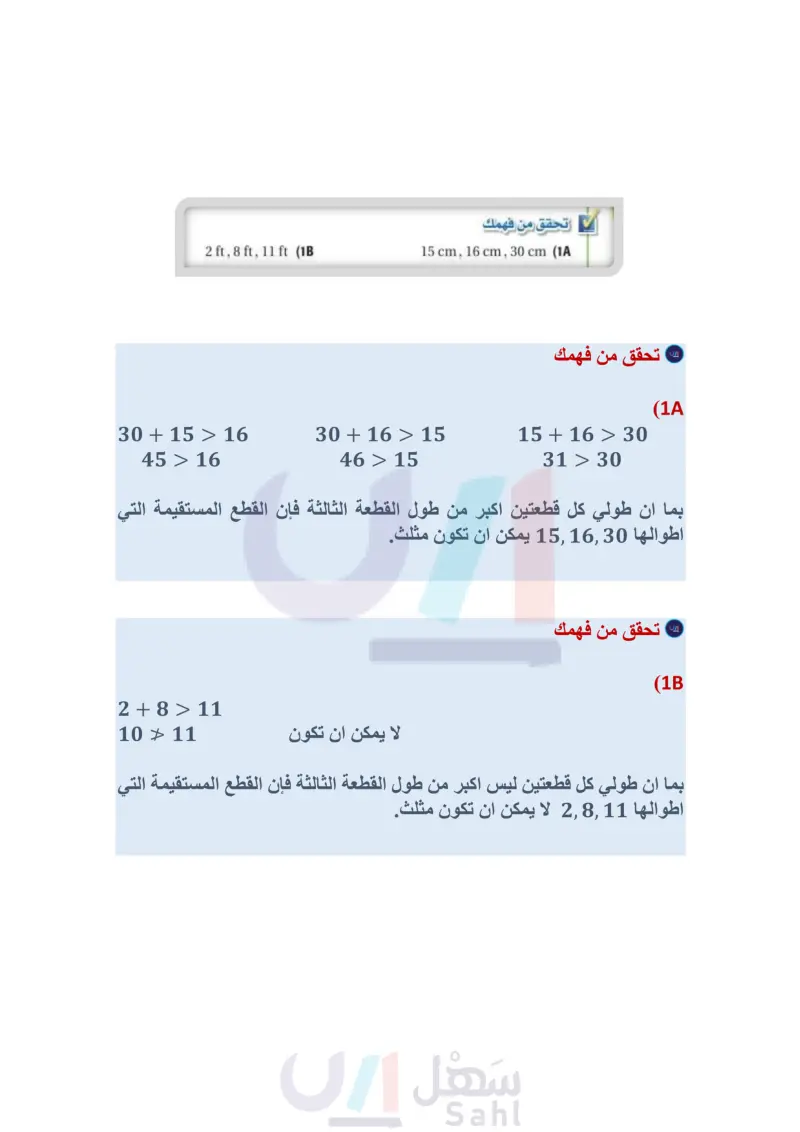
1A- حدد ما إذا كانت القياسات المعطاة يمكن أن تمثل أطوال أضلاع مثلث في كل من السؤالين الآتيين، وإذا لم يكن ذلك ممكنا، فوضح السبب:


إذا كان مجموع أقصر طولين أكبر من الضلع الثالث، فإن الأطوال الثلاثة تمثل أطوال أضلاع مثلث
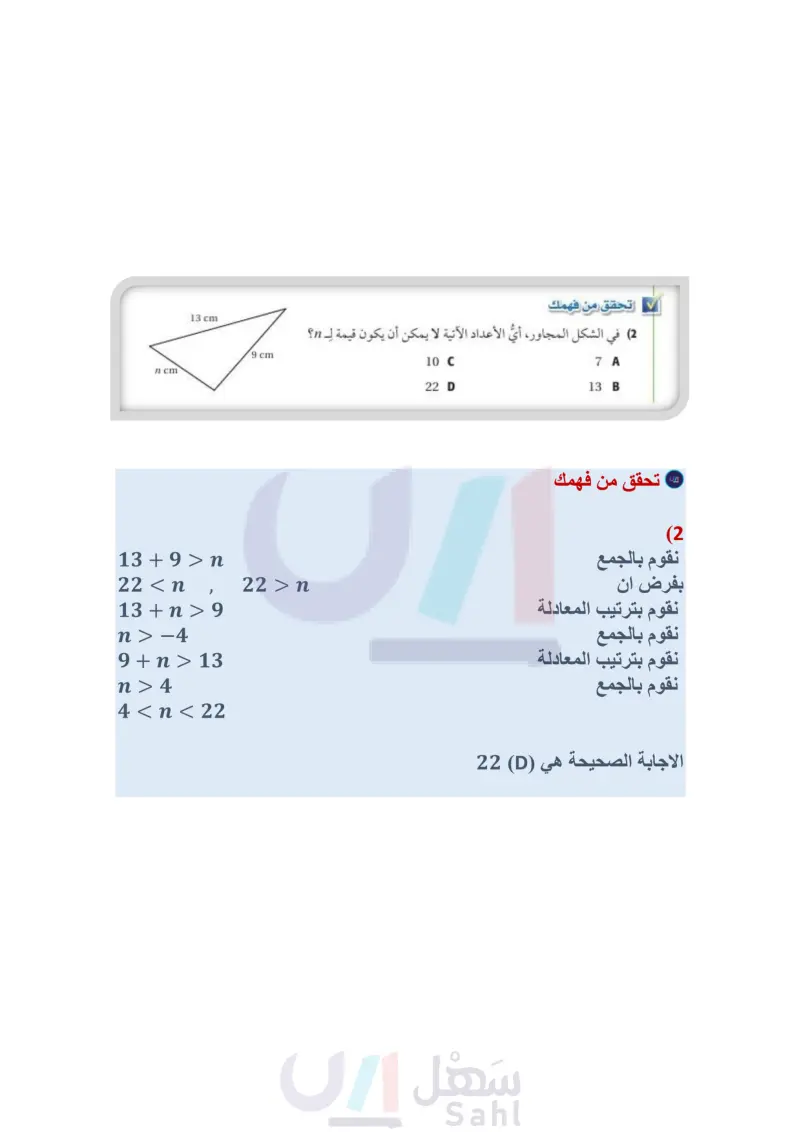
عندما يُعلم طولا ضلعين في مثلث، يمكن تحديد مدى القيم الممكنة لطول الضلع الثالث باستعمال نظرية متباينة المثلث. 5 3 مثال 2 من الاختبار إرشادات للاختبار اختبار البدائل إذا كان الوقت غير كاف يمكنك اختبار كل بديل لإيجاد الإجابة الصحيحة واستبعاد البدائل الأخرى. إذا كان طولا ضلعين في مثلث هما 3cm cm ، فما أصغر عدد طبيعي يمكن أن يمثل طول الضلع الثالث؟ 3 cm A 5 cm 4cm B C 10 cm D اقرأ فقرة الاختبار المطلوب هو تحديد أصغر قيمة ممكنة لطول الضلع الثالث في مثلث طولا ضلعين من أضلاعه 3 cm 7 cm xcm 3 cm, 7 cm حل فقرة الاختبار لتحديد أصغر طول ممكن من بين البدائل المعطاة، حدد مدى القيم الممكنة لطول الضلع الثالث أولا؛ لذا ارسم شكلا وافترض أن طول الضلع الثالث يساوي x ، ثم اكتب متباينات المثلث الثلاث، وحل كل واحدة منها. قراءة الرياضيات المتباينة المركبة تقرأ المتباينة المركبة التالي: تقع بين 3+ 7 > x 10 > x أو x < 10 3 + x 7 x> 4 x+7>3 x> -4 10 > x > 4 على النحو لاحظ أن 4 < تد تكون صحيحةً دائمًا لأي قيمةٍ صحيحة موجبة لـ x ، وبربط المتباينتين المتبقيتين، يكون مدى القيم التي تحقق كلتا المتباينتين هو 4 < x و 10 > x، والذي يمكن كتابته في الصورة 10 > x > 4 وأقل . عدد صحیح موجب بين 4 و 10 هو 5 ؛ لذا فالإجابة الصحيحة هي C. 4 و 10 أو x أكبر من 4 وأقل من 10 تحقق من فهمك (2) في الشكل المجاور ، أيُّ الأعداد الآتية لا يمكن أن يكون قيمة لـ n؟ 13 cm وزارة التعليم Ministry of Education 2024-1446 n cm 9 cm 10 C 22 D 7A 13 B الفصل 4 العلاقات في المثلث 116

اختيار البدائل
المتباينة المركبة
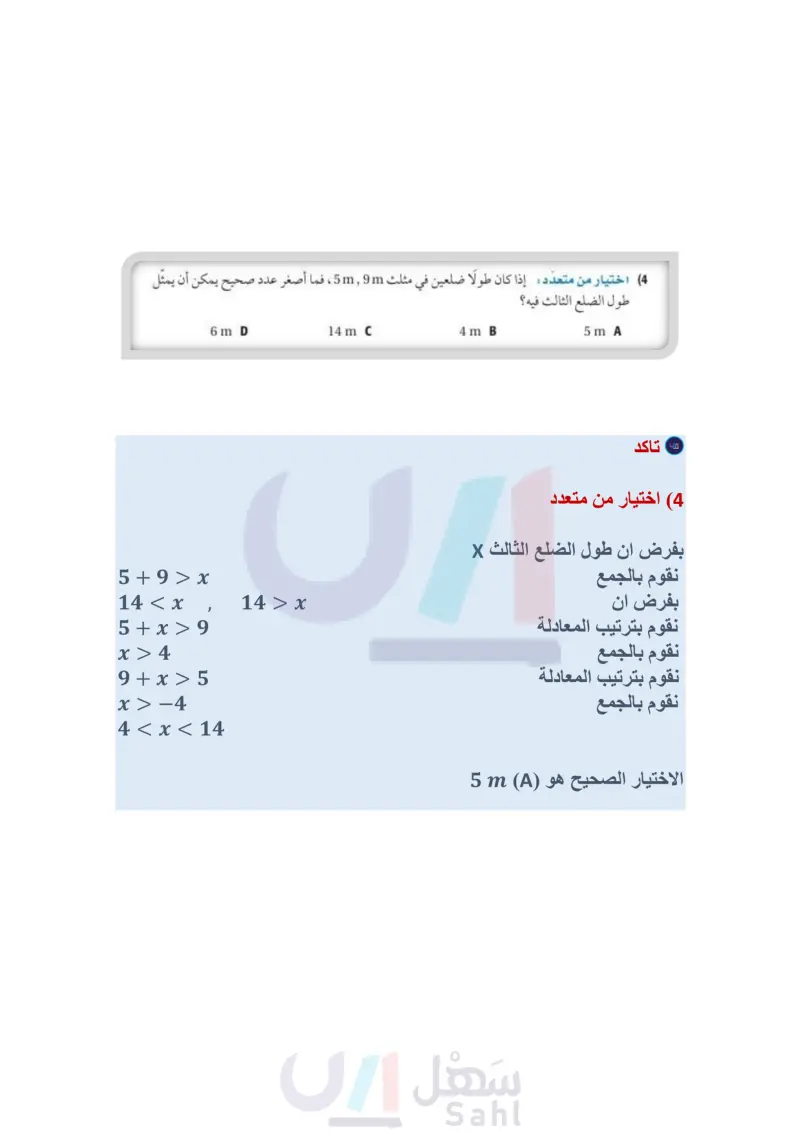
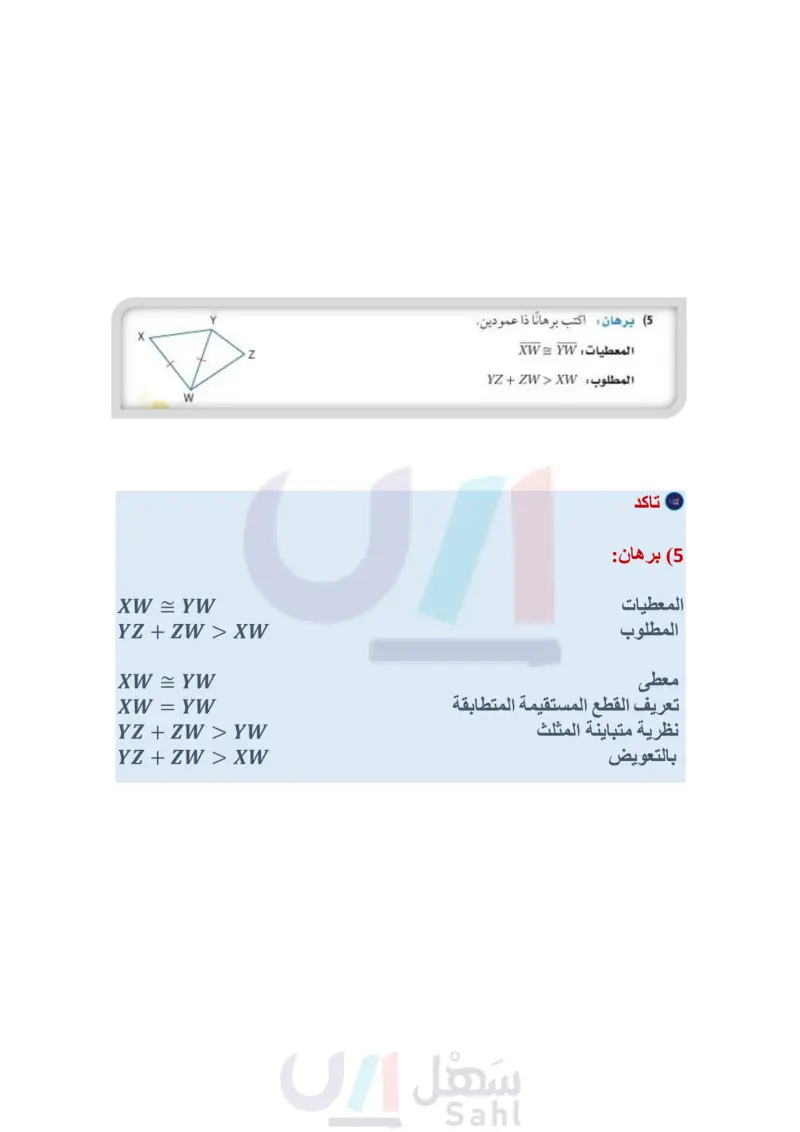
الربط مع الحياة يختلف الطيران المباشر عن الطيران من دون توقف، ففي حالة الطيران المباشر لا يغير المسافرون الطائرة، ولكن قد تحط الطائرة في مطار واحد أو أكثر قبل وصولها لغايتها. استعمال نظرية متباينة المثلث في البراهين: يمكنك استعمال نظرية متباينة المثلث في البراهين المختلفة. مثال 3 من واقع الحياة استعمال نظرية متباينة المثلث في البرهان طيران المسافة الجوية من الرياض إلى ينبع تساوي المسافة الجوية من الرياض إلى أبها، أثبت أن الطيران المباشر من الرياض إلى ينبع مرورًا بمدينة بريدة يقطع مسافة أكبر من المسافة المقطوعة عند الطيران من الرياض إلى أبها دون توقف. ارسم شكلًا تقريبياً يمثل المسألة، وضع عليه رموز أسماء المدن، وارسم القطعة YA لتشكّل AYRA . المعطيات RY = RA المطلوب : RB + BY > RA البرهان : العبارات 1) معطى B Y + R المبررات R الرياض بريدة B ° G H K (2) نظرية متباينة المثلث (3) بالتعويض RY = RA (1 RB + BY > RY (2) RB + BY > RA (3) تحقق من فهمك (3) اكتب برهانا ذا عمودين. المعطيات: GL = LK المطلوب : JH + GH > JK المثال 1 حدد ما إذا كانت القياسات المعطاة يمكن أن تمثل أطوال أضلاع مثلث في كل مما يأتي، وإن لم يكن ذلك ممكنا فوضّح السبب. 6 m, 14 m, 10 m (3) 3 in, 4 in, 8 in (2 5 cm, 7 cm, 10 cm (1) المثال 2 (4) اختيار من متعدّد إذا كان طولا ضلعين في مثلث 5mm ، فما أصغر عدد . صحيح يمكن أن يمثل طول الضلع الثالث فيه؟ X Y W 6m D 14 m C الدرس 5-4 متباينة المثلثات ال117 Ministry of E 2024-1446 4m B 5 m A المثال 3 (5) برهان اكتب برهانا ذا عمودين. المعطيات XW = YW المطلوب : YZ + ZW > XW تأكـ

حدد ما إذا كانت القياسات المعطاة يمكن أن تمثل أطوال أضلاع مثلث في كل مما يأتي، وإن لم يكن ذلك ممكنا فوضح السبب


يختلف الطيران المباشر عن الطيران من دون توقف ففي حالة الطيران المباشر لا يغير المسافرون الطائرة، ولكن قد تحط الطاشرة في مطار واحد أو أكثر قبل وصولها لغايتها
A وزارة التعليم Ministry of Education 2024-1446 تدرب وحل المسائل المثال 1 حدد ما إذا كانت كلّ من القياسات الآتية تمثل أطوال أضلاع مثلث في كل مما يأتي، وإن لم يكن ذلك ممكنا فوضح السبب. 11 mm, 21 mm, 16 mm (7) 2¹m, 1²m, 5¹¹m (9 4 ft, 9 ft, 15 ft (6 9.9 cm, 1.1 cm, 8.2 cm (8 المثال 2 اكتب متباينة تمثل مدى طول الضلع الثالث في مثلث عُلم طولا ضلعين من أضلاعه في كل مما يأتي: 5 m, 11 m (11 km, 3 km (13 4 ft, 8 ft (10 2.7 cm, 4.2 cm (12 المثال 3 برهان اكتب برهانا ذا عمودين لكل مما يأتي : 14 المعطيات: BCD = CDB المطلوب : AB + AD > BC (15) المعطيات : JL = LM المطلوب : KJ + KL > LM K M X x + 13 Z 4x-1 2x+7 A B D C جبر حدد القيم الممكنة لـد في كل من السؤالين الآتيين: (17 A (16 2x + 22 x+5 B 5x-7 C 18 قيادة يُريد توفيق أن يسلك المسار الأقصر من بيته إلى المجمع الرياضي و يمكنه أن يسلك الطريق 1 أو الطريق 2 ثم الطريق 3 . أيُّ المسارين أقصر من بيت توفيق إلى المجمع الرياضي؟ وضح إجابتك. بيت توفيق الطريق 2 الطريق 1 60km 35km افترض أن توفيقا يقود سيارته بسرعةٍ قريبة جدا من السرعة القصوى المجمع الرياضي الطريق 3 المسموح بها ولا تتعداها. إذا كانت السرعة القصوى على الطريق 1 تساوي 60km/h ، وعلى كل من الطريقين 23 تساوي 100km/h ، فأي المسارين سيستغرق وقتا أقل؟ وضح إجابتك. (19) برهان اكتب برهانا ذا عمودين. المعطيات : AABC المطلوب : AC + BATMA (نظرية متباينة المثلث) إرشاد : ارسم قطعة مستقيمة مساعدة CD ، على أن تكون C بين BD ويكون CD = AC ) . 50km C B الفصل 4 العلاقات في المثلث 118

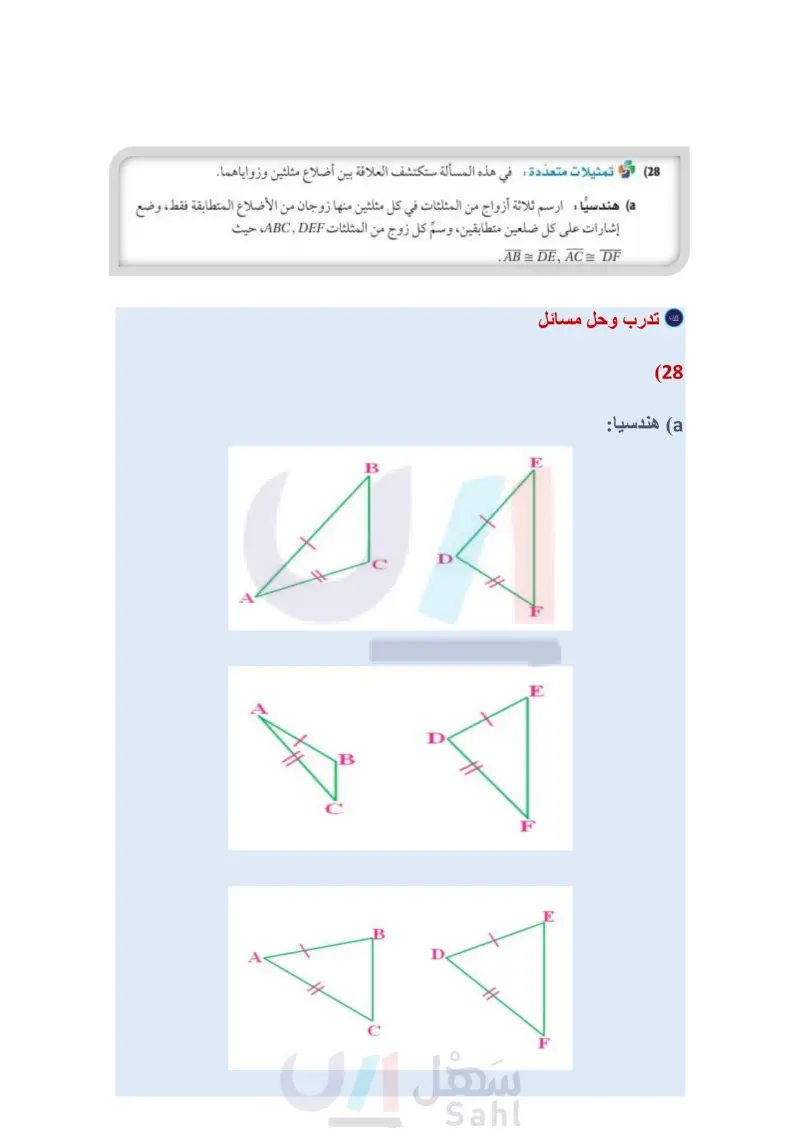
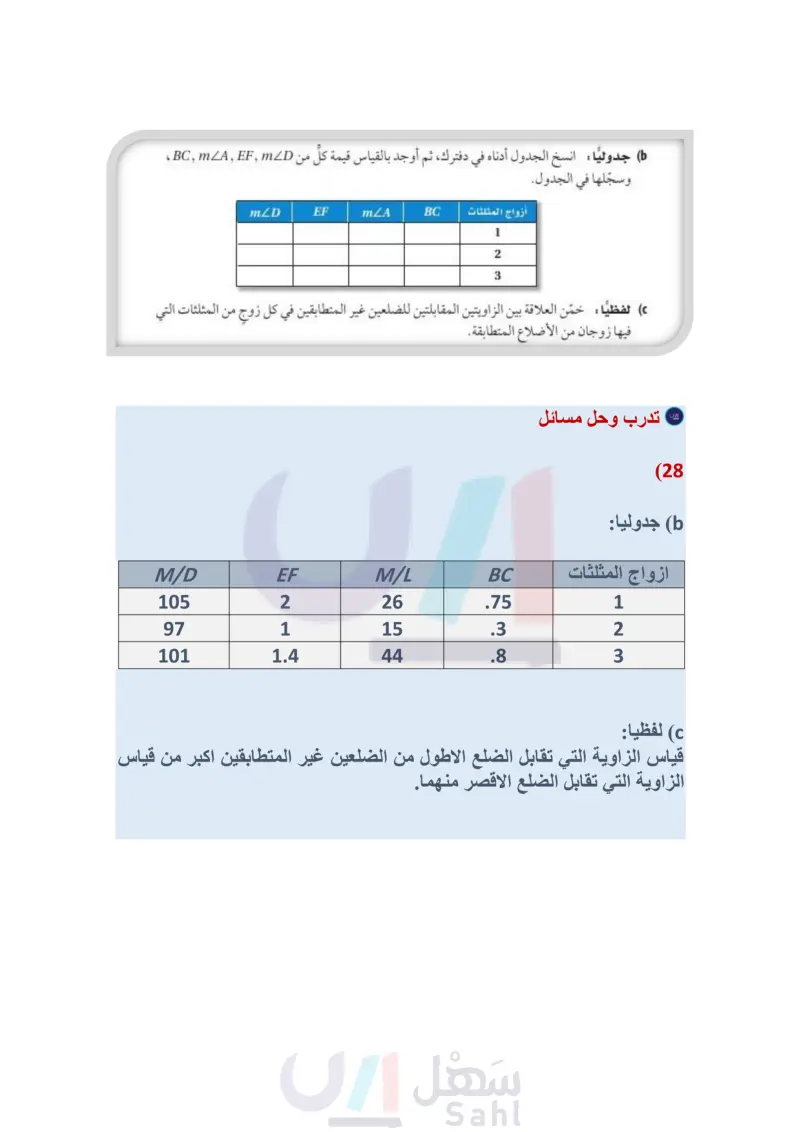
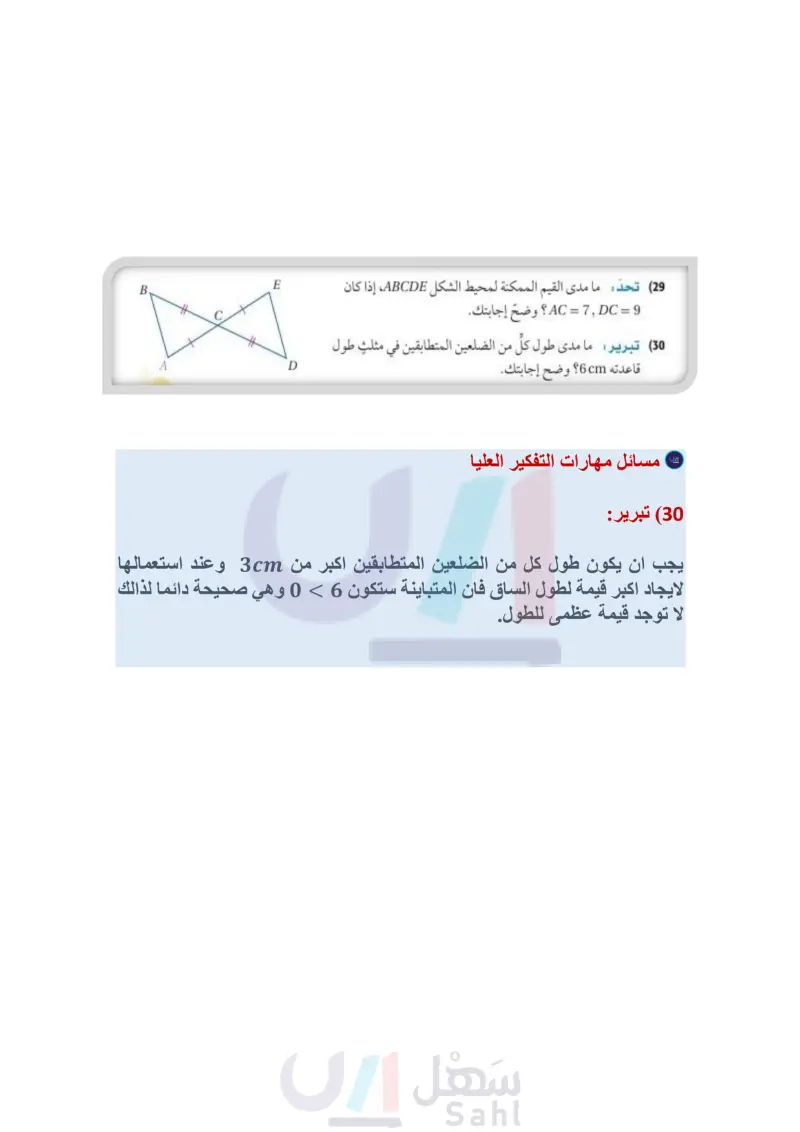
الربط مع الحياة إذا كانت كل مجموعة تمثل أطوال أضلاع مثلث، فاكتب متباينةً تمثل مدى القيم الممكنة لـ في كل من الأسئلة الآتية: x, 4, 6 (20 x + 1,5,7 (22) 8, x, 12 (21 x+2, x+4, x+6 (23 (24) مسرح يصمم عبد الرحمن وخليل منحدرا للصعود إلى منصة المسرح . فخطط عبد الرحمن المنحدر كما في الشكل أدناه، ولكن خليلا كان قلقًا بشأن القياسات ويريد أن يتحقق منها قبل البدء في قص الخشب، فهل يوجد ما يبرر هذا القلق ؟ وضح إجابتك. المنصة تصمم المسارح وفق نظام هندسي دقيق يراعى فيه إمكانية مشاهدة جميع الحضور للمنصة، وسماع الصوت بوضوح دون صدى . 75° 1 ft. تقدير: حدد ما إذا كانت القياسات المعطاة يمكن أن تمثل أطوال أضلاع مثلث في كل مما يأتي، وذلك دون استعمال الآلة الحاسبة. وضح إجابتك. √√8 ft, √2 ft, √√35 ft (25 √99 cm, √48 cm, √65 cm (26 (27) حدد ما إذا كانت النقاط (22) (1) تمثل رؤوس مثلث وضح إجابتك. (28) تمثيلات متعددة في هذه المسألة ستكتشف العلاقة بين أضلاع مثلثين وزواياهما. (a) هندسيا : ارسم ثلاثة أزواج من المثلثات في كل مثلثين منها زوجان من الأضلاع المتطابقة فقط، وضع إشارات على كل ضلعين متطابقين، وسمّ كل زوج من المثلثات ABCDEF، حيث .AB = DE, AC = DF ) جدوليا : انسخ الجدول أدناه في دفترك، ثم أوجد بالقياس قيمة كل من BC, A, EF, D ، وسجلها في الجدول. أزواج المثلثات 1 2 3 mZD EF mZA BC لفظيا : خمّن العلاقة بين الزاويتين المقابلتين للضلعين غير المتطابقين في كل زوج من المثلثات التي فيها زوجان من الأضلاع المتطابقة. مسائل مهارات التفكير العليا (29) تحد ما مدى القيم الممكنة لمحيط الشكل ABCDE، إذا كان 9 = AC = 7, DC وضح إجابتك. 30) تبرير ما مدى طول كلّ من الضلعين المتطابقين في مثلث طول قاعدته cm 6؟ وضح إجابتك. E B A الدرس 5-4 متباينة المثلثات ال119 Ministry of E 2024-1446

تصمم المسارح وفق نظام هندسي دقيق يراعي فيه إمكانية مشاهدة جميع الحضور للمنصة وسماع الصوت بوضوح دون صدى
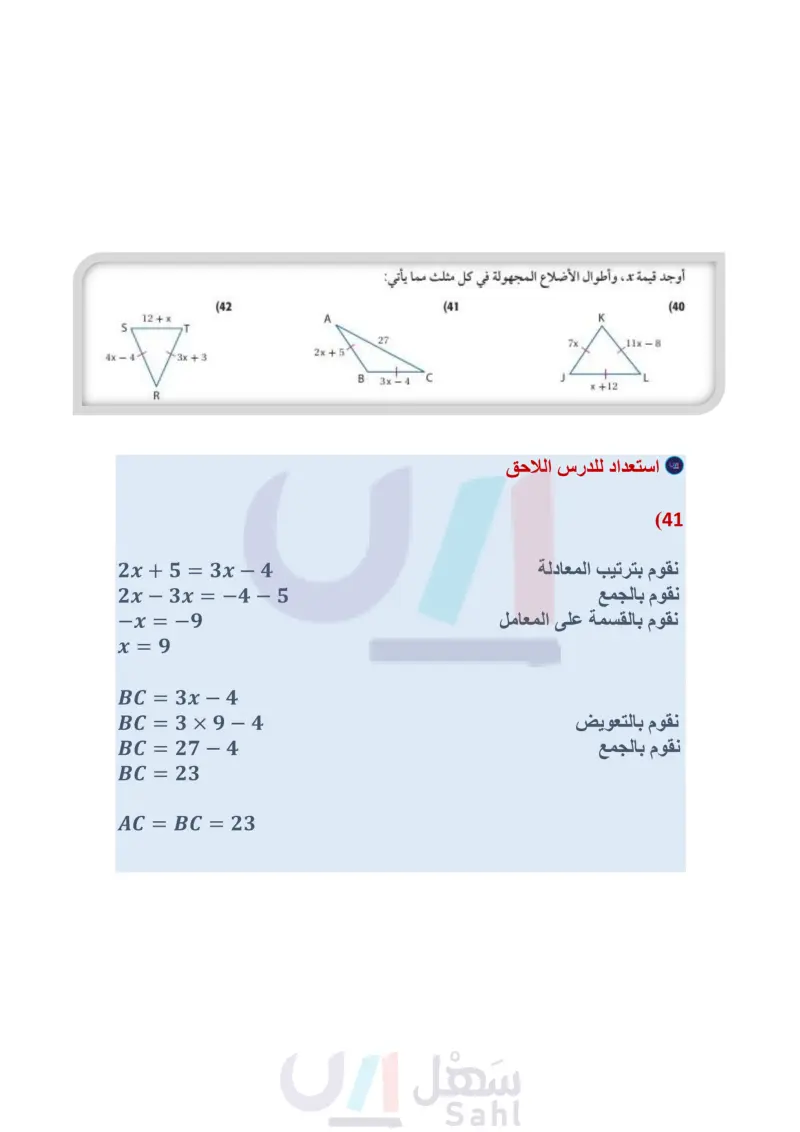
وزارة التعليم Ministry of Education 2024-1446 (31) مسألة مفتوحة : طول أحد أضلاع مثلث 5سم ارسم . مثلثًا يكون الضلع الذي طوله 5 سم أقصر أضلاعه، ومثلثاً آخر يكون الضلع الذي طوله 5 سم أطول أضلاعه مضمنًا رسمَكَ أطوال أضلاع المثلث وقياسات زواياه. (32) اكتب اشرح الطريقة التي تستعملها لإيجاد أصغر قيمة وأكبر قيمة لطول ضلع مثلث إذا علمت طولي الضلعين الآخرين. تدريب على اختبار (33) إذا كانت DC قطعةً متوسطة في AABC وكان m1 > m2 ، فأي عبارة مما يأتي غير صحيحة؟ (34) أي معادلة مما يأتي تمثل العبارة: "ناتج طرح 7 من 140 يساوي z" ؟ (7x-1) 7 - 140 = 2 A 2 = 14w + 7 B 7 z 14w C 2 = 140 - 7D 1/2 A D B AC > BC C AD = BD A mZ1mZB D mZADC=mZBCD B مراجعة تراكمية اكتب الافتراض الضروري الذي تبدأ به برهانا غير مباشر لكل عبارة مما يأتي : (الدرس 4-4) (35) إذا كان 41 = 17 + 4y، فإن 6 = y (36) إذا قطع مستقيم مستقيمين آخرين، وكانت الزاويتان المتبادلتان داخليا متطابقتين، فإنّ المستقيمين متوازيان. أوجد قيمة x ، على أن يكون 11 | 17 في كل مما يأتي، واذكر المسلّمة أو النظرية التي استعملتها : (مهارة سابقة) (39 m Y (8x+4) (9x-11)° m 1 (38 (92-51) " m n (7x-100) (37 استعد للدرس اللاحق أوجد قيمة x ، وأطوال الأضلاع المجهولة في كل مثلث مما يأتي: (42 12 + x A S 27 4x-4 3x+3 2x+5 B 3x 4 C R (41 K 7x 11x - 8 x +12 الفصل 4 العلاقات في المثلث L (40 120




 0
0 

 4
4