القطع المتوسطة والارتفاعات في المثلث - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
C القطع المتوسطة والارتفاعات في المثلث B CD قطعة متوسطة في AABC. أضف إلى مطويتك. A L B B P K F D 10 A E الت91 Medians and Altitudes of Triangle 4-2 الماذا؟ فيما سبق: درست الأعمدة المنصفة صمم مهندس طاولة خاصة لأحد الزبائن، يتكون سطحها ومنصفات الزوايا في المثلث واستعمالها والان أتعرف القطع المتوسطة في المثلث وأستعملها. أتعرف الارتفاعات في المثلث وأستعملها. المفردات: القطعة المتوسطة median من لوح زجاجي مثلث الشكل يرتكز على دعامة واحدة، ولتحقيق ذلك فهو في حاجة إلى إيجاد النقطة التي يضع عندها الدعامة لكي يحافظ على اتزانها، ويمكن إيجاد هذه النقطة بر برسم القطع المتوسطة، وتعيين نقطة تقاطعها. القطع المتوسطة: القطعة المتوسطة لمثلث قطعة مستقيمة طرفاها أحد رؤوس المثلث ونقطة منتصف الضلع المقابل لذلك الرأس. ولكل مثلث ثلاث قطع متوسطة تتلاقى في نقطة تُسـ تسمى مركز المثلث وتقع داخله دائما. نظرية مركز المثلث نظرية 4.7 يبعد مركز المثلث عن كل رأس من رؤوس المثلث ثلثي طول القطعة المستقيمة الواصلة بين ذلك الرأس ومنتصف الضلع المقابل له. مثال : إذا كانت P مركز ABC ، فإن AP= = 3 AK, BP = 3 BL CP= P = C مثال 1 استعمال نظرية مركز المثلث إذا كانت النقطة Q مركز BE = 9 ،AABC فأوجد كلا من BQQE . نظرية مركز المثلث BQ = BE BE = 9 = 3 (9) = =6 جمع أطوال القطع المستقيمة BQ + QE = 9 BQ = 6 6+ QE=9 اطرح 6 من الطرفين QE = 3 تحقق من فهمك في ABC أعلاه، إذا كان 15 = FC ، فأوجد طولي القطعتين الآتيتين : QC (1B الدرس 2-4 القطع المتوسطة والارتفاعات في المثلث . Ministry of Edu 2024-1446 FQ (1A مركز المثلث centroid الارتفاع altitude ملتقى ارتفاعات المثلث orthocenter

إرشادات للدراسة مثال 2 استعمال نظرية مركز المثلث استعمال الحسن العددي في AJKL، إذا كان 2 = PT ، فأوجد KP. في المثال 2 ، يمكنك أيضا استعمال الحس العددي لإيجاد KP . بما أن JR = RK ، فإن R نقطة منتصف JK ، وتكون LR قطعة متوسطة L في AJKL ، وبالمثل نستنتج أن ST هما نقطتا منتصفي LL على بما أن KP = KT ، فإن PT = KT وكذلك KP = 2PT ؛ لذا إذا كان 2 = PT فإن 4 = (2)2 = KP. الترتيب؛ لذا فإن SKI قطعتان متوسطتان في AJKL ، لذلك فالنقطة P هي مركز AJKL . نظرية مركز المثلث PT = 2 KP=3 KT KP = (KP + PT) KP=} (KP+2) جمع القطع المستقيمة والتعويض KP = 2 = 3 KP + } KP = KP = 4 تحقق من فهمك خاصية التوزيع اطرح KP من الطرفين اضرب الطرفين في 3 في AJKL أعلاه، إذا كان 9 = RP = 53.5, JP ، فأوجد طولي القطعتين الآتيتين: PL (2A PS (2B S K R P. جميع المضلعات لها نقطة اتزان وهذه النقطة تعتبر مركز ثقل الجسم، وهي النقطة التي يظهر فيها الجسم متوازنًا تحت تأثير الجاذبية الأرضية. مثال 3 من واقع الحياة إيجاد المركز في المستوى الإحداثي الربط مع الحياة نقطة الاتزان (التعليق) يمكن أن تحدد نقطة الاتزان لأي جسم، سواء أكان على شكل مثلث أو غيره كما يأتي: علق الجسم من أي نقطة وعندما يتوقف عن التأرجح. ارسم مستقيما رأسيًا من نقطة التعليق، ثم علقه مرة أخرى من نقطة ثانية وارسم مستقيما رأسيًا منها، فتكون نقطة تقاطع المستقيمين هي نقطة الاتزان. 92 الفصل 4 العلاقات في المثلث فن الأداء : في مهرجان رياضي يُخطط عبدالعزيز لاتزان قطع مثلثية من المعدن كما في الشكل المجاور، وعندما وضع مثلث على مستوى إحداثي كانت رؤوسه عند النقاط (9,5) ,0 ,5) ,(1,10). ما إحداثيات النقطة التي يجب على عبد العزيز أن يثبت المثلث عندها حتى يحفظه متوازنًا؟ وضح إجابتك. افهم تحتاج إلى إيجاد مركز المثلث من خلال الإحداثيات المعطاة، وستكون هذه هي النقطة التي سيتزن عندها المثلث. خطط ارسم المثلث الذي رؤوسه (9) (100)، وبما أن مركز المثلث هو النقطة التي تتلاقى عندها القطع المتوسطة للمثلث؛ إذن استعمل نظرية نقطة المنتصف لإيجاد نقطة منتصف أحد أضلاع المثلث، فيكون مركز المثلث واقعا على القطعة المتوسطة وعلى بعد من الرأس يساوي ثلثي طول القطعة المتوسطة. وزارة التعليم Ministry of Education 2024-1446

نقطة الاتزان ( التعليق)
حل مثل AABC بيانيا . أوجد نقطة المنتصف D للضلع AB الذي طرفاه D .A(1, 10), B(5, 0) 1+5 10+0 | = D(3, 5) y A(1, 10) P C(9.5)- D(3,5) عين النقطة ،D ، ولاحظ أن DC أفقية، والمسافة من (3) إلى (95) تساوي 3 - ، أي 6 وحدات. فإذا كانت P مركز AABC ، فإن PC = 0 B(5, 0) DC ؛ ولذا يقع المركز على بعد (6) ، أو 4 وحدات إلى اليسار من C وتكون إحداثيات P هي ( 4 ) أو (5) إذن يتوازن المثلث عند النقطة (55). تحقق استعمل قطعة متوسطة أخرى للتحقق من صحة إجابتك. بما أن نقطة منتصف الضلع AC 19105) أو (55) ، وأن BF رأسية فإن المسافة من B إلى F تساوي هي 0 - 7.5 ؛ أي 7.5 وحدات، وعلى ذلك يكون PB يساوي (7.5) أي 5 ، إذن P تقع على بعد 5 وحدات إلى أعلى من B. وتكون إحداثيات هي (5) أي (5) تحقق من فهمك 3) تقع رؤوس مثلث آخر عند النقاط (2) 6.5 (04) ، فما إحداثيات النقطة التي يتزن عندها هذا المثلث؟ وضح إجابتك. ارتفاعات المثلث ارتفاع المثلث هو القطعة المستقيمة العمودية النازلة من أحد الرؤوس إلى المستقيم الذي قراءة الرياضيات يحوي الضلع المقابل لذلك الرأس، ويمكن أن يقع الارتفاع داخل المثلث أو خارجه أو على أحد أضلاعه. ارتفاع المثلث يطلق اسم الارتفاع على القطعة وعلى طولها، ويفهم المقصود من سياق المسألة. ويستعمل الارتفاع لحساب مساحة المثلث. B A A A DC BD هو الارتفاع من B إلى AC B AB هو الارتفاع إلى CB. ولكل مثلث ثلاثة ارتفاعات تتلاقى المستقيمات التي تحويها في نقطة مشتركة. مفهوم أساسي ملتقى الارتفاعات تتقاطع المستقيمات التي تحوي ارتفاعات أي مثلث في نقطة تُسمّى ملتقى الارتفاعات. :مثال تتقاطع المستقيمات التي تحوي الارتفاعات F, CD, G عند النقطة P ، وهي ملتقى الارتفاعات للمثلث ABC . B أضف إلى مطويه ك F D P ப A G الدرس 2- القطع المتوسطة والارتفاعات في المثلث ال93 Ministry of Ede 2024-1446

يطلق اسم ارتفاع المثلث على القطعة وعلى طولها، ويفهم المقصود من سياق المسألة
P يمكن أن تلتقي الارتفاعات في مثلث داخله أو خارجه أو على أحد أضلاعه. P مثلث حاد الزوايا مثلث منفرج الزاوية مثال 4 إيجاد ملتقى الارتفاعات في المستوى الإحداثي مثلث قائم الزاوية هندسة إحداثية : إذا كانت رؤوس AFGH هيا (1-2) ,4 ,4 ,4 ,2-F، فأوجد إحداثيات ملتقى ارتفاعاته. الخطوة 1: مثل AFGH بيانيا. ولإيجاد ملتقى الارتفاعات، أوجد نقطة تقاطع ارتفاعين من الارتفاعات الثلاثة الخطوة 2: أوجد معادلة الارتفاع من F إلى GH بما أن ميل GH يساوي 2 4-(-2) 4-1 فإنّ ميل الارتفاع العمودي على GH يساوي - y-y₁m(x-x₁) 1-4 = - [x - (2) صيغة النقطة والميل y F(-2.4) G(4,4) H(1,-2) 0 (x1,y) = F(-2, 4),m= --- بسط خاصية التوزيع y - 4= - = √(x+2) y-4= y =-11x+3 إرشادات للدراسة التحقق من المعقولية استعمل ركن ورقة لرسم ارتفاعات المثلث. اجمع 4 إلى الطرفين ثم أوجد معادلة الارتفاع من G إلى FH. بما أن ميل FH يساوي 2 - = 2 ، فإن ميل الارتفاع العمودي على FH يساوي -2-4 (-2) y-y₁ =m(x-x1) صيغة النقطة والميل (x1,y1) G(4, 4), m= y- 1 - 4 = }(x - 4) خاصية التوزيع اجمع 4 إلى الطرفين لإيجاد نقطة تقاطع الارتفاعات. y - 4 = } X-2 y: y=} x+2 y = y = - x + 3 الخطوة 3: حل نظام المعادلتين الناتج اجمع المعادلتين لتحذف x ، فينتج أن 5 = 2y ، ومن ثم فإن } = y معادلة الارتفاع من G y= = 3 x + 2 5 = = =x + 2 2 1=x اطرح ، أو 2 من الطرفين اضرب الطرفين في 2 إذن إحداثيات ملتقى ارتفاعات AFGH هي (12) أو (12) وزارة التعليم Ministry of Education 2024-1446 y F(-2,4) TG(4,4) نقطة التقاطع تقع تقريبا عند (1,2) لذا فالجواب معقول. الفصل 4 العلاقات في المثلث 94

التحقق من المعقولية
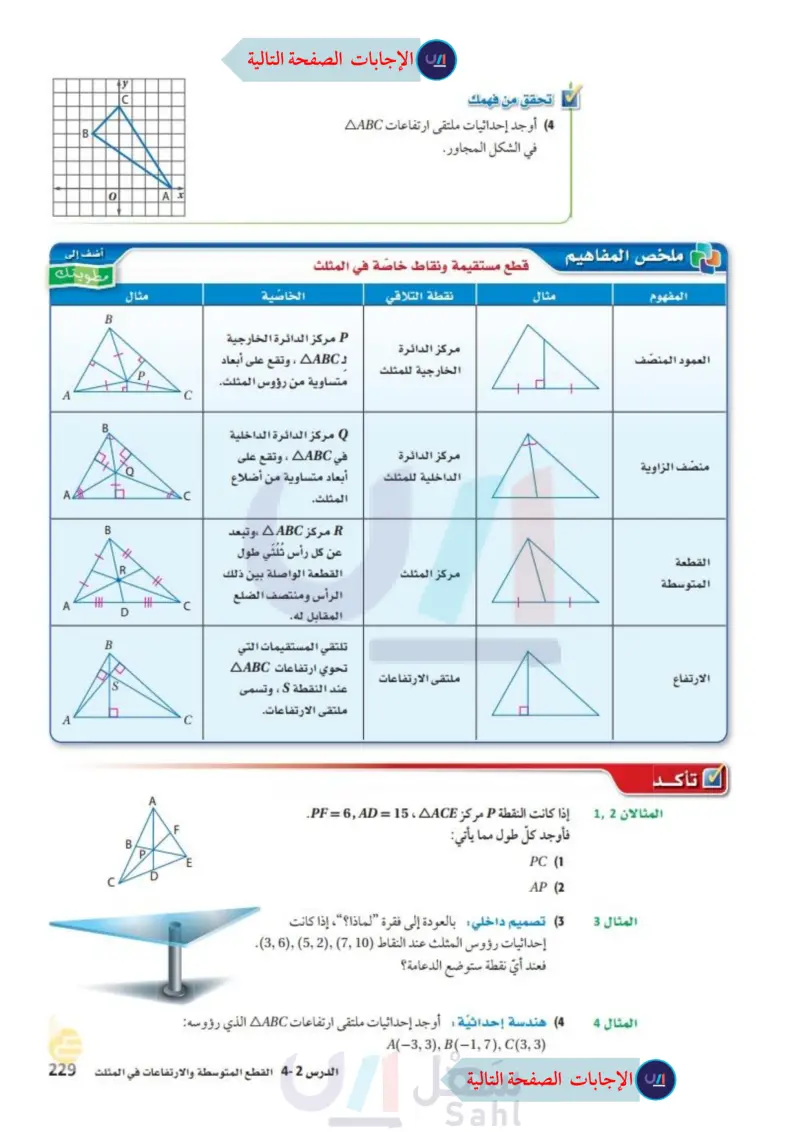
ملخص المفاهيم المفهوم العمود المنصف تحقق من فهمك (4) أوجد إحداثيات ملتقى ارتفاعات AABC في الشكل المجاور. مثال قطع مستقيمة ونقاط خاصة في المثلث نقطة التلاقي الخاصية P مركز الدائرة الخارجية مركز الدائرة الخارجية للمثلث د AABC ، وتقع على أبعاد متساوية من رؤوس المثلث مركز الدائرة منصف الزاوية القطعة المتوسطة مركز الدائرة الداخلية في AABC ، وتقع على الداخلية للمثلث أبعاد متساوية من أضلاع المثلث مركز AABC ، وتبعد عن كل رأس ثلثي طول مركز المثلث القطعة الواصلة بين ذلك الرأس ومنتصف الضلع المقابل له. تلتقي المستقيمات التي تحوي ارتفاعات AABC الارتفاع ملتقى الارتفاعات عند النقطة S ، وتسمى ملتقى الارتفاعات. تأكد المثالان 1 إذا كانت النقطة P مركز PF = 6, AD = 15 ، AACE. فأوجد كل طول مما يأتي: PC (1 AP (2 المثال 3 (3) تصميم داخلي: بالعودة إلى فقرة "لماذا؟"، إذا كانت إحداثيات رؤوس المثلث عند النقاط (710) ,(52) ,(36). فعند أي نقطة . ستوضع | الدعامة؟ Ax 0 أضف إلى مطويتك مثال F B Έ D R D B B B B A المثال 4 (4) هندسة إحداثية: أوجد إحداثيات ملتقى ارتفاعات AABC الذي رؤوسه A(-3, 3), B(-1, 7), C(3, 3) الدرس 2- القطع المتوسطة والارتفاعات في المثلث الت95 2024-1446

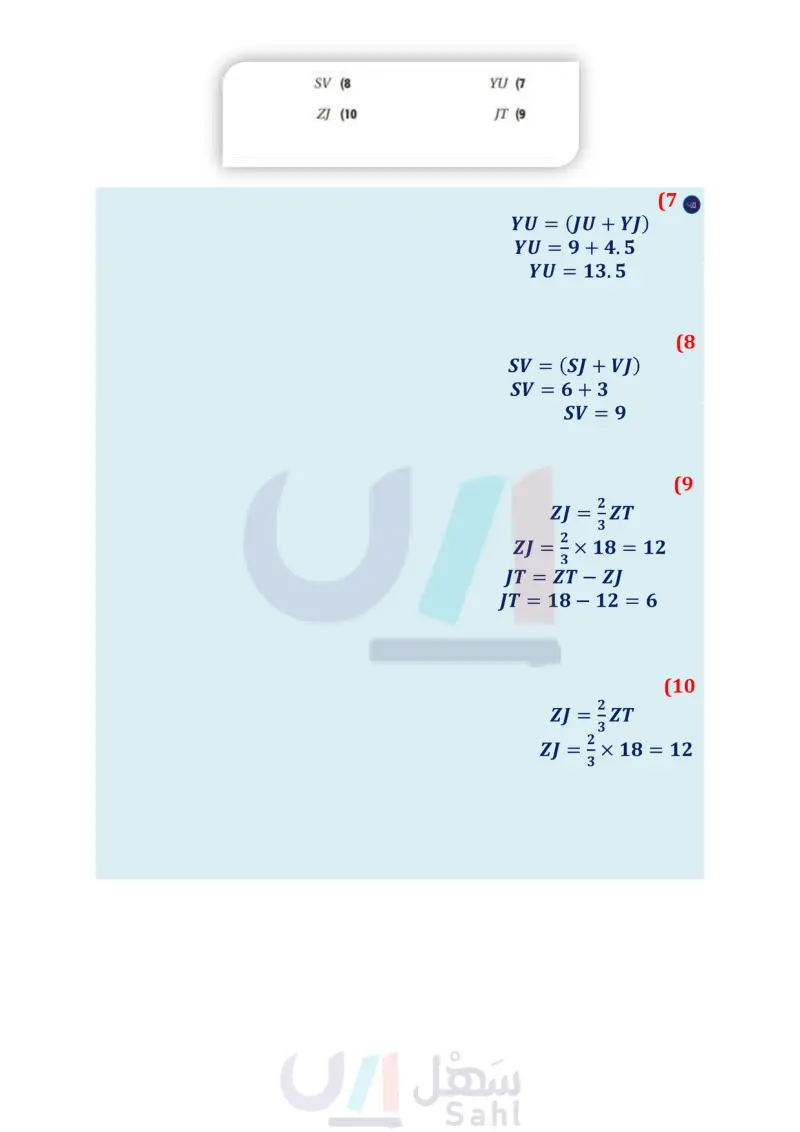
A وزارة التعليم Ministry of Education 2024-1446 9 تدرب وحل المسائل المثالان 1 في ASZU ، إذا كان 18 = ZT ، فأوجد كل طول مما يأتي: SJ (6 YJ (5 SV (8 YU (7 ZJ (10 JT (9 المثال 3 11) تصميم داخلي : صنعت كوثر لوحةً مثلثة الشكل كما في الشكل أدناه لتضع عليها صور معالم مشهورة. وأرادت أن تعلقها في سقف حجرتها على أن تكون موازية له. فعند أي نقطة يجب أن تُثبت الخيط ؟ B E 0 (0,8) (3,0) (6.4) المثال 4 (12) هندسة إحداثية: أوجد إحداثيات ملتقى الارتفاعات للمثلث الذي رؤوسه J(3,-2), K(5, 6), L(9,-2) صنف BD في كلّ من الأسئلة الآتية إلى ارتفاع، أو قطعة متوسطة، أو عمود منصف: H (22 2x-bp M D 15 14 B D C 13 16 جبر في الشكل المجاور ، إذا كانت PL, نقاط منتصفات KH, K على الترتيب، فأوجد قيمة كل من x 17 جبر في الشكل المجاور ، إذا كانت EC ارتفاعًا لـ AAED " (13 + m1 = (2x + 7)", m22 = (3x ، فأوجد كلا من mZ1, mz2 الفصل 4 العلاقات في المثلث 96 96

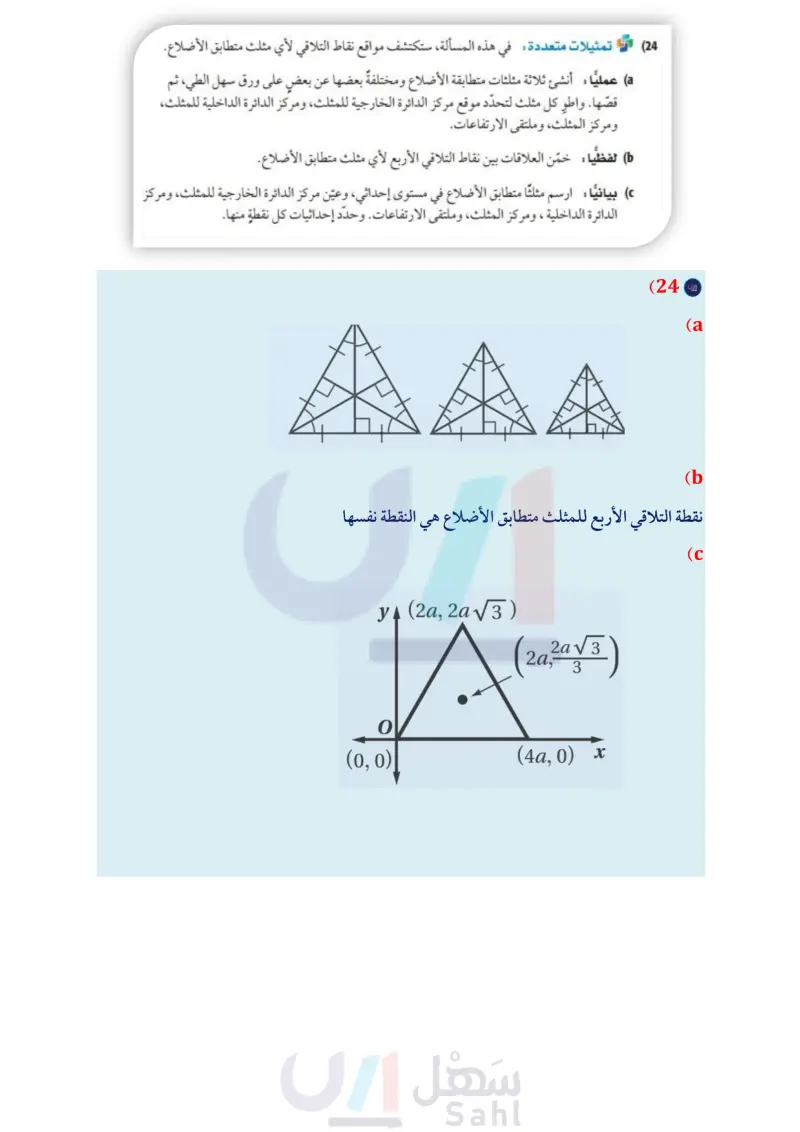
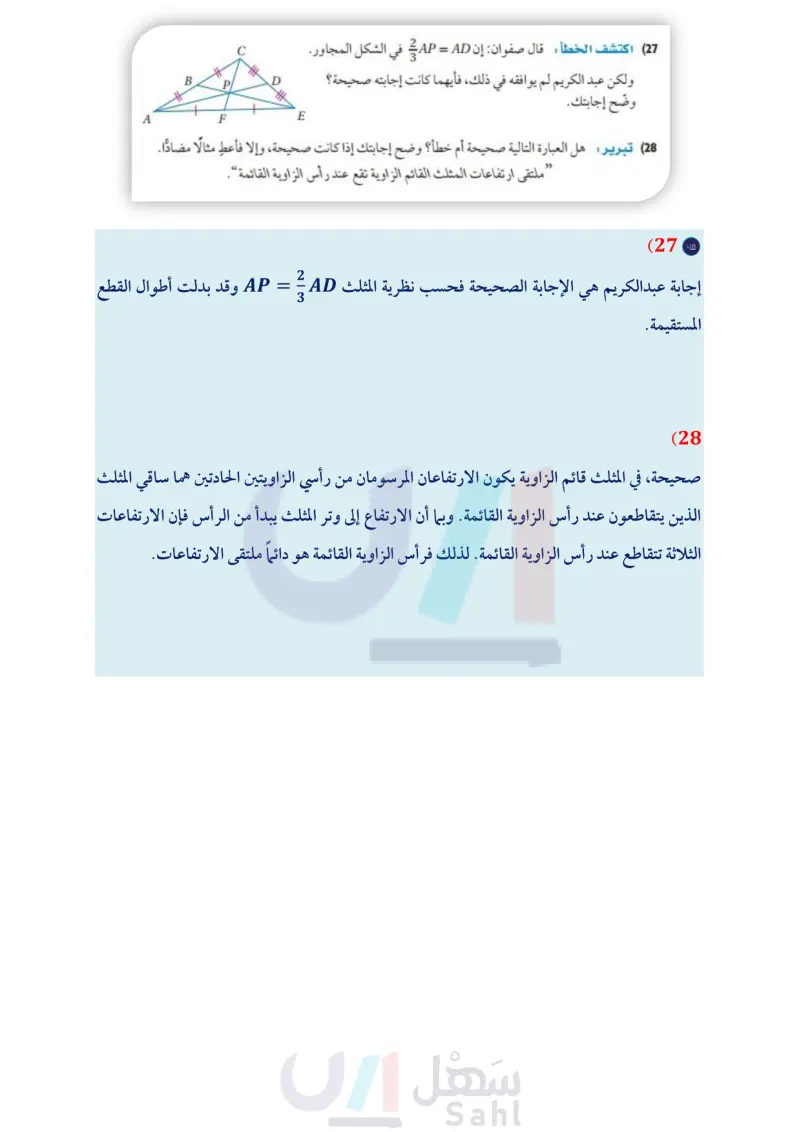
في الشكل المجاور، حدد ما إذا كانت LM عمودًا منصفا، أو قطعة متوسطة ، أو ارتفاعًا لـ AJKL في كل حالة مما يأتي: J M K AJLM = AKLM (19 LMJK, JL KL (21 LMJK (18 JMKM (20 (22) برهان اكتب برهانا حرا. المعطيات: AXYZ متطابق الضلعين فيه (23) برهان اكتب برهانا ذا عمودين. المعطيات: X, Y, ZQ قطع متوسطة لـ AXYZ WY تنصف XY = ZY Y المطلوب : WY قطعة متوسطة. المطلوب : 2 = XP PR ° R P Z X S X W Z (24) التمثيلات متعددة في هذه المسألة، ستكتشف مواقع نقاط التلاقي لأي مثلث متطابق الأضلاع. عمليا: أنشئ ثلاثة مثلثات متطابقة الأضلاع ومختلفةً بعضها عن بعض على ورق سهل الطي، ثم قصها. واطو كل مثلث لتحدّد موقع مركز الدائرة الخارجية للمثلث، ومركز الدائرة الداخلية للمثلث، ومركز المثلث، وملتقى الارتفاعات لفظيا : خمّن العلاقات بين نقاط التلاقي الأربع لأي مثلث متطابق الأضلاع. بيانيا : ارسم مثلثاً متطابق الأضلاع في مستوى إحداثي، وعيّن مركز الدائرة الخارجية للمثلث، ومركز الدائرة الداخلية، ومركز المثلث، وملتقى الارتفاعات. وحدد إحداثيات كل نقطة منها. A M mZJMP = (3x-6)°, JK = 3y-2, LK-5y-8. AJLP (25) إذا كانت M ارتفاعًا لـ AJLP ، فأوجد x . (26) إذا كانت PK قطعة متوسطة، فأوجد LK مسائل مهارات التفكير العليا (27) اكتشف الخطأ قال صفوان: إن AP = AD في الشكل المجاور. ولكن عبد الكريم لم يوافقه في ذلك، فأيهما كانت إجابته صحيحة ؟ وضح إجابتك. E C Pl F B (28) تبرير هل العبارة التالية صحيحة أم خطأ؟ وضح إجابتك إذا كانت صحيحة، وإلا فأعط مثالا مضادًا. ملتقى ارتفاعات المثلث القائم الزاوية تقع عند رأس الزاوية القائمة“. الدرس 2- القطع المتوسطة والارتفاعات في المثلث الت 97 Ministry of Education 2024-1446

اكتب برهانا ذا عمودين
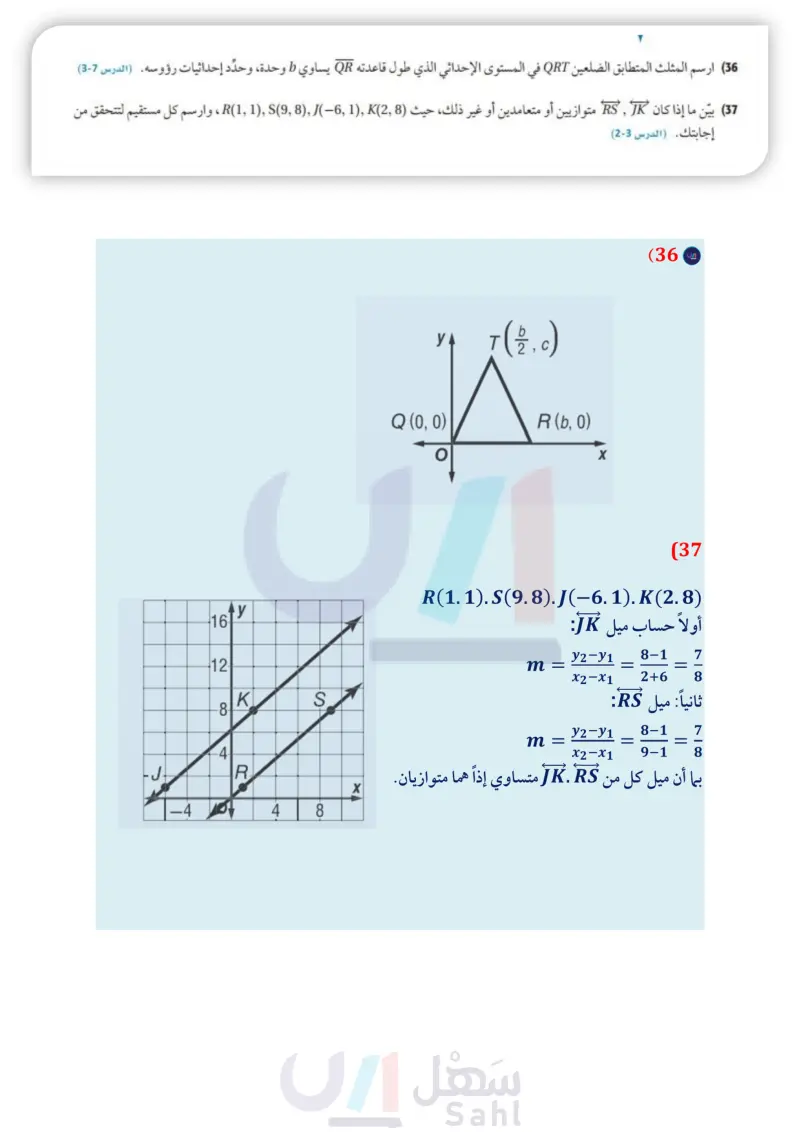
C وزارة التعليم Ministry of Education 2024-1446 B (29) تحد في الشكل المجاور ، إذا كانت ADC قطعتين متوسطتين في AACB ، وكانت 29 = AD I CE, AB 2010 ,CE، فأوجد CA (30) اكتب: استعمل المساحة لتفسر لماذا يكون مركز المثلث هو نقطة اتزانه، ثم استعمل هذا التفسير لوصف موقع نقطة اتزان المستطيل. تدريب على اختبار R x + 3 (32) ما المقطع x للمستقيم 12 = 4x - 6y ؟ -3 C -2 D TQ (35 7 S 7 T 2x-6 3 A 2 B D 10 G H Η (31) في الشكل المجاور، إذا كان GJ = H ، فأي عبارة مما يأتي صحيحة ؟ FA ارتفاع لـ AFGH FB منصف زاوية في AFGH FC قطعة متوسطة في AFGH عمود منصف في AFGH DF (34 مراجعة تراكمية أوجد كل قياس مما يأتي : : ( الدرس (1-4) 8.5 8.5 M 6 E L * LM (33 (36) ارسم المثلث المتطابق الضلعين QRT في المستوى الإحداثي الذي طول قاعدته QR يساوي ط وحدة، وحدد إحداثيات رؤوسه. (الدرس (7-3) 37) بين ما إذا كان متوازيين أو متعامدين أو غير ذلك، حيث (2)(6) ,(98) ,(11) ، وارسم كل مستقيم لتتحقق من إجابتك (مهارة سابقة ) -4.25 -19 (41 2.70 (40 استعد للدرس اللاحق اكتب < أو > داخل لتحصل على عبارة صحيحة. (39 الفصل 4 العلاقات في المثلث (38 98




 0
0 

 0
0