زوايا المثلثات - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
3-2 زوايا المثلثات Angles of Trangles فيما سبق: درست تصنيف المثلثات وفقًا لقياسات أضلاعها وزواياها ( الدرس (1-3) والان أطبق نظرية مجموع قياسات زوايا المثلث أطبق نظرية الزاوية الخارجية للمثلث. المفردات: المستقيم المساعد auxiliary line المادة يرعى أحد معاهد التقنية مسابقة سنوية، حيث يصمم الطلاب روبوتا آليا يؤدّي مهام مختلفة. وقد تمت برمجة هذا الروبوت الآلي في أحد الاختبارات ليتحرك في مسار على شكل مثلث. على أن يكون مجموع قياسات الزوايا التي ينعطف فيها الروبوت الآلي عند نقاط الارتكاز الثلاث ثابتاً دائما. نظرية مجموع قياسات زوايا المثلث : تُعبر نظرية مجموع قياسات زوايا المثلث عن العلاقة بين الزوايا الداخلية لأي مثلث. نظرية 3.1 نقطة ارتكاز 1 نظرية مجموع قياسات زوايا المثلث التعبير اللفظي: مجموع قياسات زوايا المثلث يساوي 180 مثال: mZA + mZB + mLC = 180° نقطة ارتكاز 3 نقطة ارتكاز 2 1 B الزاوية الخارجية exterior angle الزاويتان الداخليتان البعيدتان remote interior angles البرهان التسلسلي flow proof النتيجة corollary 20 20 الفصل 3 المثلثات المتطابقة www.len.edu.sa تشغيل / إنهاء أضف إلى مطوية ـك A يتطلب برهان نظرية مجموع قياسات زوايا المثلث استعمال مستقيم مساعد، والمستقيم المساعد هو مستقيم إضافي ( أو قطعة مستقيمة إضافية ) يتم رسمه للمساعدة على تحليل العلاقات الهندسية، وكما تُبرر العبارات والاستنتاجات المُستعملة في البرهان، فإن خصائص المستقيم المساعد يجب تبريرها. برهان نظرية مجموع قياسات زوايا المثلث المعطيات: AABC المطلوب : 180 = m21 + mZ2 + m23 -> البرهان من النقطة A ارسم المستقيم AD موازيا لـ BC. AABC (1 العبارات 1) معطى A D B C المبررات (2) BAD, زاويتان متجاورتان على مستقيم (2) تعريف الزاويتين المتجاورتين على مستقيم 3 4BAD, متكاملتان. mZ4+mZBAD = 180° (4 mLBAD = m22 + m25 (5 mZ4 + mZ2 + m25 = 180° (6) Z421, 2523 (7 m24 m21, mZ5=mZ3 (8 m1 + mZ2 + m23 = 180° (9 (3) الزاويتان المتجاورتان على مستقیم متكاملتان (4) تعريف الزاويتين المتكاملتين (5) مسلّمة جمع قياسات الزوايا (6) بالتعويض (7) نظرية الزاويتين المتبادلتين داخليا (8) تعريف تطابق الزوايا 9) بالتعويض وزارة التعليم Ministry of Education 2024-1446

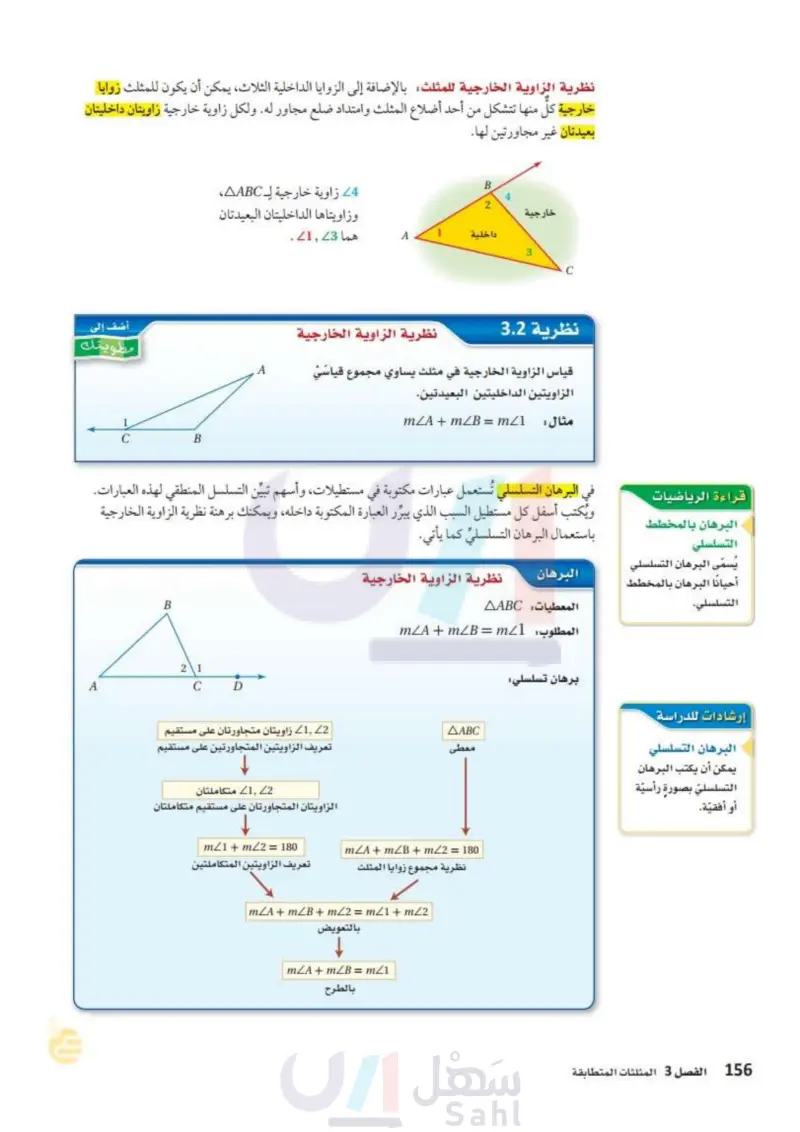
يمكن استعمال نظرية مجموع قياسات زوايا المثلث لإيجاد الزاوية الثالثة في المثلث إذا عُلم قياسا زاويتيه الأخريين. مثال 1 من واقع الحياة استعمال نظرية مجموع زوايا المثلث كرة قدم : يبين الشكل مسار الكرة في تدريب على تمريرات نفذها أربعة لاعبين. أوجد قياسات الزوايا المرقمة. 20 B 78 C 2 الربط مع الحياة يدمج تمرين "مرر وتحرك" في لعبة كرة القدم بين عدة مظاهر أساسية لعملية التمرير، حيث تكون جميع التمريرات في التدريب على 61° E افهم : المعطيات في الشكل أعلاه، قياس الزاويتين في المثلث ABC 208 قياس الزاوية E في المثلث CED يساوي °61 المطلوب إيجاد قياسات الزوايا المرقمة. شكل مثلثات ، وهذا هو الأساس خطط أوجد m3 باستعمال نظرية مجموع زوايا المثلث مستعملا قياسي الزاويتين الأخريين AABC. ثم استعمل نظرية الزاويتين المتقابلتين بالرأس لإيجاد 2 2 m، وعندها يمكنك في جميع حركات الكرة وبالإضافة إلى ذلك، على اللاعب أن يتحرك فورا بعد تمريره الكرة. في إيجاد m1 في ACDE m23 + mZBAC + mLACB = 180° نظرية مجموع زوايا المثلث عوض بسط اطرح 98 من الطرفين m23 + 20° + 78° = 180° m23 + 98° = 180° m23 = 82 ACB متطابقتان؛ لأنهما زاويتان متقابلتان بالرأس؛ لذا فإن "78 = m22. استعمل m2 و MLCED في ACDE لإيجاد m1. إرشادات للدراسة تجزئة المسألة تجزأ المسائل المركبة إلى مسائل يمكن m21+ mZ2 + mZCED = 180° m/178° + 61° = 180° mZ1 + 139° = 180° m1 = 41° نظرية مجموع زوايا المثلث عوض بسط اطرح 139 من الطرفين التعامل مع كل منها تحقق يجب أن يكون مجموع قياسات زوايا كلَّ من ABC, ACDE مساويا لـ 180 بسهولة؛ مما يساعد على حلها. فمثلا في المثال 1: عليك أن تجد m2 أولا قبل أن تحاول إيجاد m21 /AABC: m/3+mZBAC+ mZACB = 82° + 20° + 78° = 180° / ACDE: m21 + m22 + mZCED = 41° + 78° + 61° = 180° تحقق من فهمك أوجد قياسات الزوايا المرقمة فيما يأتي: Y 58° (18) X/7 V 65° Z 5/6 9 W الدرس 2 زوايا المثلثات الت21 2024-1446 1 L 57° 28 71 K (1A M

يدمج تمرين " مرر وتحرك" في لعبة كرة القدم بين عدة مظاهر اساسية لعملية التمرير
تجزئة المسألة
22 22 نظرية الزاوية الخارجية للمثلث بالإضافة إلى الزوايا الداخلية الثلاث، يمكن أن يكون للمثلث زوايا خارجية كل منها تتشكل من أحد أضلاع المثلث وامتداد ضلع مجاور له ولكل زاوية خارجية زاويتان داخليتان بعيدتان غير مجاورتين لها. B 2 خارجية داخلية 3 C 4 زاوية خارجية لـ AABC وزاويتاها الداخليتان البعيدتان . 21, 23 Las A 1 نظرية 3.2 نظرية الزاوية الخارجية قياس الزاوية الخارجية في مثلث يساوي مجموع قياسي الزاويتين الداخليتين البعيدتين مثال : mZA + mZB = mZ1 A أضف إلى مطويتك 1 C B قراءة الرياضيات في البرهان التسلسلي تُستعمل عبارات مكتوبة في مستطيلات، وأسهم تبين التسلسل المنطقي لهذه العبارات. ويُكتب أسفل كل مستطيل السبب الذي يبرّر العبارة المكتوبة داخله، ويمكنك برهنة نظرية الزاوية الخارجية البرهان بالمخطط التسلسلي يُسمى البرهان التسلسلي أحيانا البرهان بالمخطط التسلسلي. باستعمال البرهان التسلسلي كما يأتي. نظرية الزاوية الخارجية البرهان المعطيات: AABC المطلوب : mZA + mZB = m1 B برهان تسلسلي : إرشادات للدراسة البرهان التسلسلي يمكن أن يكتب البرهان التسلسلي بصورة رأسية أو أفقية. الفصل 3 المثلثات المتطابقة AABC معطى mZA+mZB+mZ2 = 180 2 1 A C D زاويتان متجاورتان على مستقيم تعريف الزاويتين المتجاورتين على مستقيم 12 متكاملتان الزاويتان المتجاورتان على مستقيم متكاملتان m/1+ mZ2 = 180 نظرية مجموع زوايا المثلث تعريف الزاويتين المتكاملتين mZA+mZB+ m/2 = m/1+ mz2 بالتعويض mZA+mZB=mZ1 بالطرح وزارة التعليم Ministry of Education 2024-1446

البرهان التسلسلي
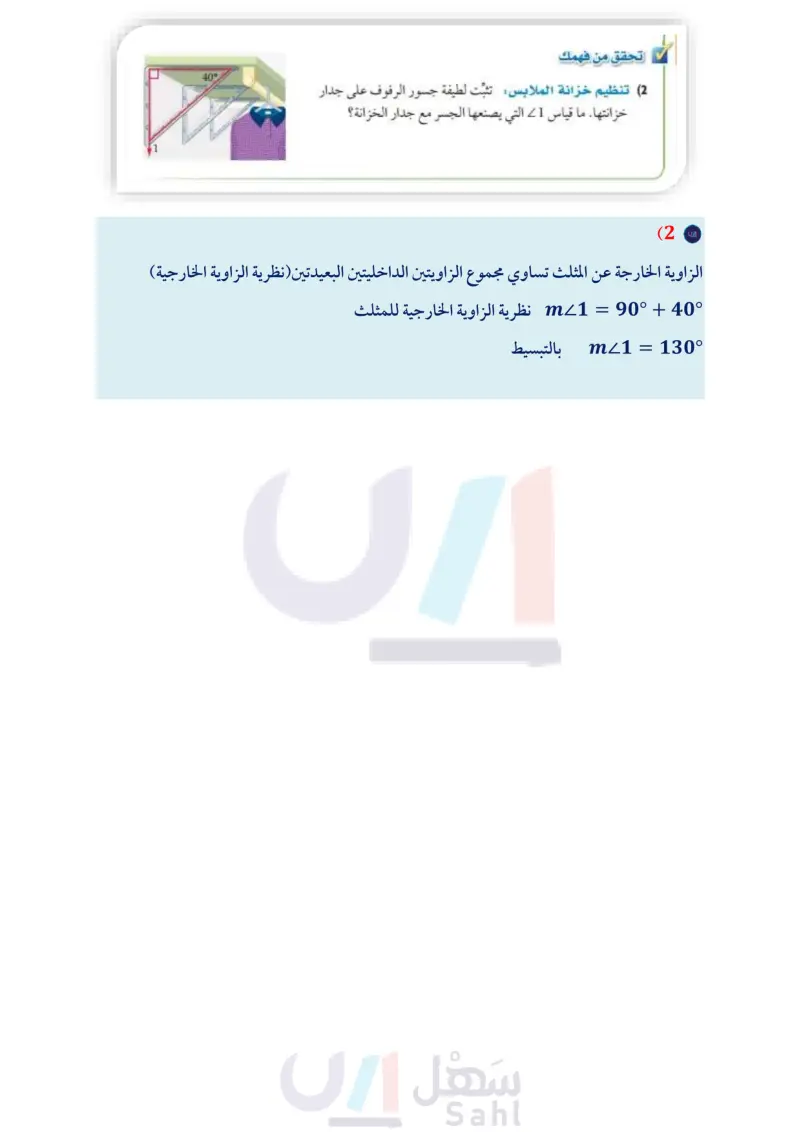
يمكن إيجاد قياسات الزوايا المجهولة باستعمال نظرية الزاوية الخارجية. مثال 2 من واقع الحياة استعمال نظرية الزاوية الخارجية اللياقة البدنية: أوجد قياس JKL في الوضع الذي يظهر فيه المتدرب في الصورة. mZKLM+mZLMK=mZJKL x + 50 = 2x - 15 50 = x - 15 65 = X نظرية الزاوية الخارجية عوض اطرح x من الطرفين اجمع 15 إلى الطرفين الربط مع الحياة المدرب المتخصص يعلم مدربو اللياقة البدنية المتدربين طرائق متنوعة ويحفزونهم على أدائها، ومن المهم أن يحمل هؤلاء المدربون لذا فإن 115 = 15 - (65)2) = mJKL. تحقق من فهمك (2) تنظيم خزانة الملابس : تثبت لطيفة جسور الرفوف على جدار خزانتها. ما قياس 1 التي يصنعها الجسر مع جدار الخزانة؟ M (2x-15) K 50° 40° شهادات تخصص في مجال النتيجة هي نظرية يكون برهانها مبنيا على نظرية أخرى، ويمكن استعمال النتيجة كأي نظرية أخرى لتبرير خطوات برهان آخر، أو حلّ أسئلة ذات علاقة، وفيما يلي نتائج مباشرة لنظرية مجموع زوايا المثلث عملهم. إرشادات للدراسة التحقق من المعقولية عندما تجد قياسات زوايا مثلث تأكد دائما أن نتيجتان مجموع زوايا المثلث 3.1 الزاويتان الحادتان في أي مثلث قائم الزاوية متتامتان. مثال: إذا كانت C قائمة، فإن زاويتان متتامتان 3.2 توجد زاوية قائمة ،واحدة أو زاوية منفرجة واحدة على الأكثر في أي مثلث. مثال: إذا كانت L قائمة، فإن زاويتان حادتان ستبرهن النتيجتين 3.2 3.1 في السؤالين 2324 مثال 3 إيجاد قياسات الزوايا في مثلثات قائمة الزاوية مجموع هذه القياسات أوجد قياس كل من الزوايا المرقمة في الشكل المجاور. يساوي 180. mZ1 + mZTYZ = 90° m21 + 52° = 90° m1 = 38° تحقق من فهمك Z2 (3A زاويتان حادتان في مثلث قائم الزاوية عوض اطرح 52 من الطرفين Z3 (3B W Z4 (3C K B L أضف إلى مطويتك A Z 52° ☑ 38° Y الدرس 2 زوايا المثلثات الت23 Ministry of Ex 2024-1446

المدرب المتخصص
التحقق من المعقولية
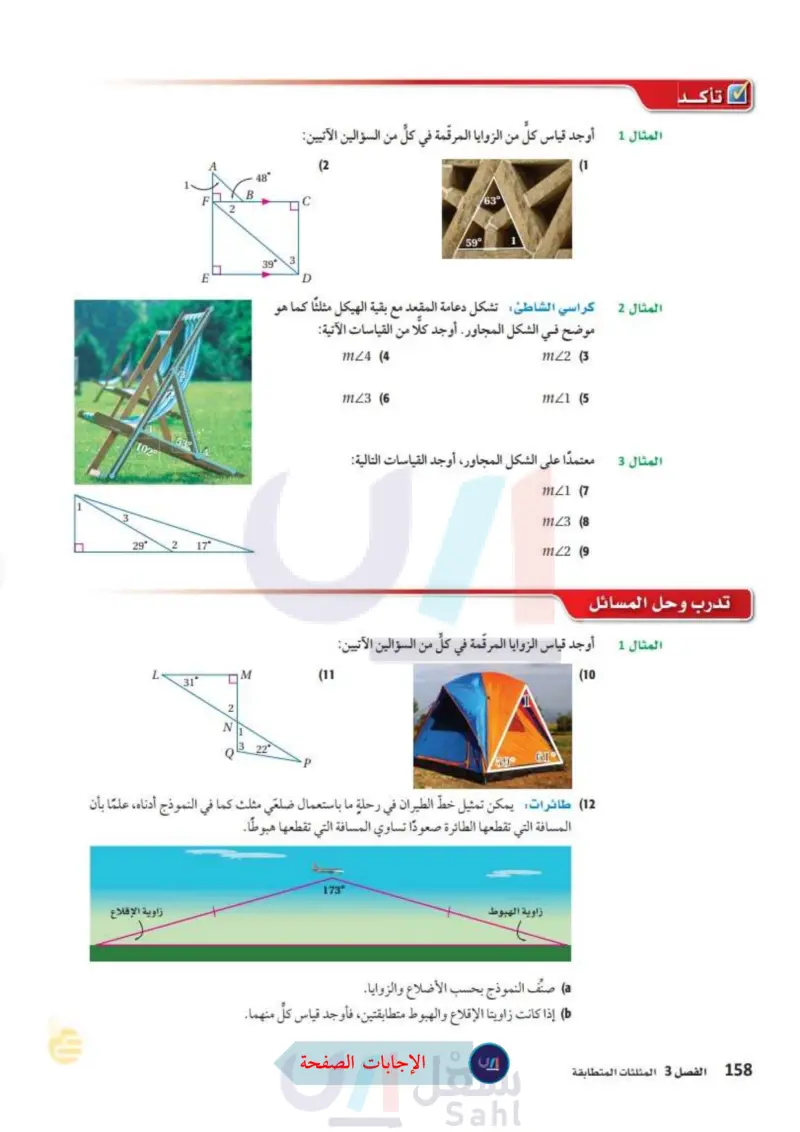
وزارة التعليم Ministry of Education 2024-1446 102° 29 2 17° المثال 1 أوجد قياس كل من الزوايا المرقمة في كل من السؤالين الآتيين: (2 48° 39° D 59° /63° (1 المثال 2 كراسي الشاطئ: تشكل دعامة المقعد مع بقية الهيكل مثلثاً كما ه موضح في الشكل المجاور أوجد كلا من القياسات الآتية: هو M (11 31° 2 N 13 22° Q m24 4 m23 (6 mz2 (3 mz1 (5) المثال 3 معتمدا على الشكل المجاور، أوجد القياسات التالية: mZ1 (7 m23 8 m22 (9 تأكد تدرب وحل المسائل المثال 1 أوجد قياس الزوايا المرقمة في كل من السؤالين الآتيين: 59 (10 (12) طائرات يمكن تمثيل خط الطيران في رحلةٍ ما باستعمال ضلعي مثلث كما في النموذج أدناه، علما بأن المسافة التي تقطعها الطائرة صعودًا تساوي المسافة التي تقطعها هبوطاً. زاوية الإقلاع 173° زاوية الهبوط a) صنف النموذج بحسب الأضلاع والزوايا. ) إذا كانت زاويتا الإقلاع والهبوط متطابقتين، فأوجد قياس كل منهما. الفصل 3 المثلثات المتطابقة 24

mZABC (15 B (2x-15)° (x-5)° AD 25° 51° 148° C 111 35° 2 123° mZ4 (14 mz2 (17 m25 (19 28° mZ6 (21 المثال 2 أوجد كلا من القياسات الآتية: 27° 52° m21 (13 المثال 3 أوجد كلًا من القياسات الآتية: m21 (16 mz3 (18 mZ4 (20 والربط مع الحياة (22) بستنة : استَنْبَتَ مهندس زراعي زهور أقحوان في حوض على شكل مثلث متطابق الضلعين. إذا رغب المهندس في أن يكون قياس A ثلاثة أمثال قياس كل من B، فما قياس كل زاوية في هذا المثلث؟ براهين برهن كلا مما يأتي مستعملًا طريقة البرهان يصل طول ساق زهرة الأقحوان إلى 30in ، وتنقسم هذه النباتات إلى 13 صنفا بحسب أشكال أزهارها. المذكورة. (23) النتيجة 3.1 باستعمال البرهان التسلسلي أوجد قياس كل من الزوايا المرقمة فيما يأتي: (24) النتيجة 3.2 باستعمال البرهان الحر (15x + 1)° (6x+5)° 110° 8 7 5 30° 130 (4x-1) 6 3 (26 4 70° 335 جبر: صنف ال المثلث في الشكل المجاور وفقا لزواياه. وفسر إجابتك. (25 (27 28) قرر ما إذا كانت العبارة الآتية صحيحة أم خطاً، واذكر مثالا مضادا لها إذا كانت خطاً، ودعم استنتاجك إذا كانت صحيحة "إذا كان مجموع زاويتين حادتين في مثلث أكبر من 90 ، فإن المثلث حاد الزوايا ". الدرس 2 زوايا المثلثات الت25 2024-1446

يصل طول ساق زهرة الأقحوان إلى 30in وتنقسم النباتات إلى 13 صنفا بحسب أشكال أزهارها.
وزارة التعليم Ministry of Education 2024-1446 37° 3, B 70° 71° (29) سيارات: انظر إلى الصورة المجاورة أوجد m1, m2. إذا قل ارتفاع غطاء السيارة عن الارتفاع الذي يظهر في الصورة، فما أثر ذلك في m21 ؟ فسّر إجابتك. إذا قل ارتفاع غطاء السيارة عن الارتفاع الذي يظهر في الصورة، فما أثر ذلك في m2؟ فسر إجابتك. برهان برهن كلا مما يأتي باستعمال طريقة البرهان المذكورة: (30) برهان ذو عمودين المعطيات: RSTUV شكل خماسي. المطلوب : 31) برهان تسلسلي المعطيات: 25 = 3 المطلوب : mZ1 + m22 = m6 + m7 3 4 5 mZS+mZSTU+mZTUV+mZV+mZVRS = 540° S R T تنبيه : قياس الزوايا عند استعمال المنقلة لقياس زاوية ما، اجعل خط التدريج 0 منطبقا على أحد ضلعي الزاوية ومركز المنقلة منطبقا على رأس الزاوية. V U (32) تمثيلات متعددة في هذه المسألة ستستكشف مجموع قياسات الزوايا الخارجية للمثلث. a) هندسيا : ارسم خمسة مثلثات مختلفة، ومد الأضلاع وسم الزوايا كما في الشكل المجاور ، على أن يكون ضمن المثلثات التي رسمتها على الأقل مثلث منفرج الزاوية، وآخر قائم الزاوية، ومثلث حاد الزوايا. (6) جدوليًا : قس الزوايا الخارجية لكل مثلث. وسجل القياسات ومجموعها لكل مثلث في جدول. لفظيا : خمّن مجموع الزوايا الخارجية للمثلث، واكتب تخمينك. جبريًا : عبّر عن التخمين الذي وصلت إليه في الجزء C جبريًا. تحليليا اكتب برهانًا حرًّا لإثبات التخمين الذي توصلت إليه. 2 A 93° 130° a/110° مسائل مهارات التفكير العليا (33) اكتشف الخطأ قام خالد بقياس زوايا المثلث وكتبها كما في الشكل. فقال عادل: إن هناك خطاً في هذه القياسات وضّح بطريقتين مختلفتين على الأقل كيف توصل عادل إلى هذه النتيجة. (34) اكتب : فسر كيف يمكنك إيجاد القياسات المجهولة في الشكل المجاور ؟ الفصل 3 المثلثات المتطابقة 26

قياس الزوايا
135° (5y + (5) (4z+9) (9y-2)° 35) تحد أوجد قيمة كل من لا في الشكل المجاور. (36) تبرير: إذا كانت الزاوية الخارجية المجاورة لـ A حادة، فهل ABC حاد الزوايا أم قائم الزاوية أم منفرج الزاوية أم أنه لا يمكن تحديد نوعه؟ وضح إجابتك. (38) أي العبارات التالية تصف العلاقة الصحيحة بين الزاويتين ab تدريب على اختبار 37 جبر أي المعادلات الآتية تكافئ المعادلة في الشكل أدناه ؟ b a + b < 90° A 7x 3(2 5x) = 8x 2x - 6 = 8 A 22x - 6 = 8x B -8x - 6 = 8x 22x + 6 = 8x D a + b = 90° a + b = 45° D a + b > 90° B 44° الدرس 2 زوايا المثلثات الت27 Ministry of Edu 2024-1446 مراجعة تراكمية صنف كلا من المثلثات الآتية إلى حاد الزوايا أو متطابق الزوايا أو منفرج الزاوية أو قائم الزاوية (مهارة سابقة) 46° (41 (40 150° 18°/ 12° 60° 60% 60% (39 هندسة إحداثية : أوجد المسافة بين النقطة P والمستقيم ) في كلّ من السؤالين الآتيين. (مهارة سابقة) (42) المستقيم يمر بالنقطتين (1), (2 ,0) ، وإحداثيا النقطة ( هما (44) (43) المستقيم يمر بالنقطتين (30) (3) ، وإحداثيا النقطة ( هما (43) استعد للدرس اللاحق اكتب الخاصية المستعملة (الانعكاس التماثل التعدي) في كل عبارة مما يلي: AB = AB (44 (45) إذا كان 1 2 ، فإن 22 = 1 . (46) إذا كانت 24 22 23 ، فإن 4 = 3 .




 0
0