المتباينات في مثلثين - رياضيات 1-2 - أول ثانوي

4-6 المتباينات في مثلثين Inequalities in Two Triangles الماذا؟ فيما سبق: درست المتباينات في المثلث الواحد. والان أطبق متباينة SAS أو عكسها لإجراء مقارنات بين عناصر مثلثين أثبت صحة العلاقات باستعمال متباينة SAS أو عكسها. تستعمل الرافعة عند تغيير إطارات السيارات، والرافعة المبينة أدناه واحدة من الرافعات البسيطة التي ما زالت تُستعمل حتى يومنا هذا. لاحظ أنه عندما تُنزَّلُ الرافعة فإنّ ساقي AABC يظلان متطابقين، في حين تزداد الزاوية A اتساعا ويزداد طول الضلع BC المقابل لـ LA متباينة ضلعين والزاوية المحصورة بينهما (SAS) : الملاحظة في المثال أعلاه صحيحة لأي نوع من المثلثات وتوضّح النظريتين الآتيتين: نظريتان المتباينات في مثلثين 4.12 متباينة SAS B إذا طابق ضلعان في مثلث ضلعين مناظرين في مثلث آخر، وكان قياس الزاوية المحصورة في المثلث الأول أكبر من قياس الزاوية المحصورة في المثلث الثاني، فإن الضلع الثالث في المثلث الأول يكون أطول من الضلع الثالث في المثلث الثاني. G C مثال: إذا كان AB = FG, AC = FH, mLA > mLF ، .BC > GHL 4.13 عکس متباينة SSS) SAS) إذا طابق ضلعان في مثلث ضلعين مناظرين في مثلث آخر، وكان الضلع الثالث في المثلث الأول أطول من الضلع الثالث في المثلث الثاني، فإن قياس الزاوية المحصورة في المثلث الأول يكون أكبر من قياس الزاوية المحصورة في المثلث الثاني مثال: إذا كان : PR = JL , QR = KL , JK ، .mZR>mZLU Н 43° Q 12 8 R K ستبرهن النظرية 4.12 في الصفحة التالية ، وستبرهن النظرية 4.13 في السؤال 18 مثال 1 استعمال متباينة SAS وعكسها قارن بين القياسين المحددين في كل من السؤالين الآتيين : L W- X Y WX, XY (a 51 55 في المثلثين WXZYXZ أضف إلى ــك A B 3.6 C mZFCD, mZBFC (b في المثلثين BCF, DFC F 3 D BFDC, FC = CF, BC > FD WZ=YZ, XZXZ, mZYZX> mZWZX وبحسب متباينة SAS فإن WX < XY وبحسب عكس متباينة SAS فإن mZBFCmZDCF الدرس 6-4 المتباينات في مثلثينة ال121م Ministry of Edu 2024-1446

B تحقق من فهمك قارن بين القياسات المعطاة في كلُّ من السؤالين الآتيين : R mSRT, mZVRT (18 8 S 6 15 M T 8 V 11 E 61° JK, MQ (1A P K 12 12 72° J L Q 15 إرشادات للدراسة متباينتا SS SAS تُعرف المتباينة SAS باسم متباينة الرافعة وعكسها يُعرف برهان متباينة SAS المعطيات في المثلثين ABCDEF AC DF, BC EF, mZF > mZC المطلوب : DE > AB البرهان D تعلم أن: AC = PDF , EF ، وتعلم أيضًا أن: mZF > mC . A F ارسم نصف المستقيم FP ، على أن يكون mDFP = m, F = BC ، وهذا سيقودنا إلى حالتين هما : الحالة 1 P تقع على DE، وعندها يكون AFPD = ACBA بحسب SAS ، لذا يكون PD = BA ؛ لأن العناصر المتناظرة في المثلثين المتطابقين تكون متطابقة، وبحسب تعريف تطابق القطع المستقيمة E D B ومسلمة جمع قياسات القطع المستقيمة يكون DE = EP + PD ؛ لذا يكون DE > PD بناءً على تعريف المتباينة، وبالتعويض يكون DE > AB الحالة 2 P لا تقع على DE وعندئذٍ سم نقطة تقاطع FED بالحرف T ، وارسم القطعة المستقيمة المساعدة FQ على أن تكون Q على DE ، وتكون EFQ E QFP ، ثم ارسم القطعتين المستقيمتين المساعدتين PDPQ . وزارة التعليم Ministry of Education 2024-1446 B A F معطى خاصية التعدي للتطابق خاصية الانعكاس للتطابق شرط تحديد النقطة ) مسلمة SAS تطابق العناصر المتناظرة تعريف التطابق شرط تحديد النقطة مسلمة SAS تطابق العناصر المتناظرة تعريف التطابق متباينة المثلث بالتعويض مسلمة جمع أطوال القطع المستقيمة بالتعويض بالتعويض D FP=BC, BCEF, AC = DF FP = EF QF=QF LEFQ = LQFP AEFQ = APFQ EQ = PQ EQ = PQ mZDFP=mZC AFPD = ACBA PD = BA PD = BA QD + PQ > PD QD + EQ > PD ED = QD + EQ ED > PD ED> BA بالمتباينة SSS. الفصل 4 العلاقات في المثلث 122

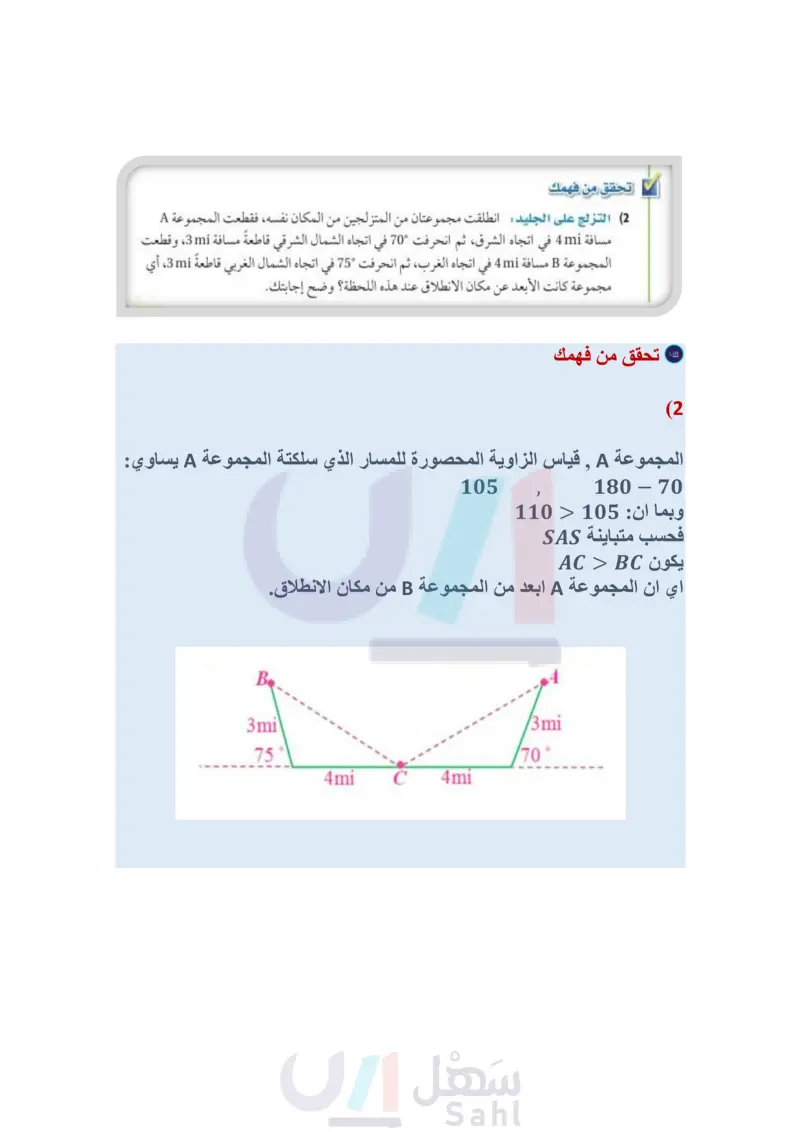
الربط مع الحياة ظهرت رياضة التزلج على الجليد في منتصف القرن التاسع عشر، ونظمت أول بطولة لها عام 1891م وهي رياضة مشهورة في البلاد الباردة، مثل كندا والدول الاسكندنافية. يمكنك استعمال متباينة SAS لحل مسائل من واقع الحياة. مثال 2 من واقع الحياة استعمال متباينة SAS التزلج على الجليد في إحدى صالات التزلج، انطلق اثنان من المتزلجين على الجليد من المكان نفسه، فقطع المتزلج A مسافة 17.5m في اتجاه الغرب، ثم انحرف 35 في اتجاه الشمال الغربي قاطعا 15m، بينما قطع المتزلج B مسافة 17.5m في اتجاه الشرق، ثم انحرف °40 في اتجاه الشمال الشرقي قاطعا 15m ، أيُّهما كان الأبعد عن مكان الانطلاق عند هذه اللحظة؟ وضح إجابتك. افهم المعطيات: قطع المتزلج A مسافة 17.5m في اتجاه الغرب، ثم انحرف 35 في اتجاه الشمال الغربي قاطعا 15m والمتزلج B قطع مسافة 17.5m في اتجاه الشرق، ثم انحرف 40° في اتجاه الشمال الشرقي قاطعا .15m. المطلوب: أيهما كان أبعد عن مكان الانطلاق. خطط : ارسم شكلا لهذا الوضع. شمال B A إرشادات لحل رسم شكل توضيحي ارسم شكلا لمساعدتك على فهم المسألة اللفظية وتوضيحها بصورة صحيحة. 15 m 15 m 35° 40° 17.5 m C 17.5 m المسار الذي اتبعه كل متزلج وبعده عن مكان الانطلاق يشكل مثلثا؛ إذ قطع كل متزلج 17.5m ، ثم انحرف وقطع 15m أخرى. استعمل أزواج الزوايا المستقيمة لإيجاد قياس الزاويتين المحصورتين، ثم طبق متباينة SAS؛ لتقارن بين بعدي المتزلجين عن مكان الانطلاق. حل قياس الزاوية المحصورة لمسار المتزلج A يساوي 35 - 180 أو "145، وقياس الزاوية المحصورة لمسار المتزلج B يساوي 40 - °180 أو 140 بما أن " 140 < "145 ، إذن A B بحسب متباينة SAS؛ لذا فالمتزلج A أبعد عن مكان الانطلاق من المتزلج .B . تحقق المتزلج B انحرف 5 أكثر مما فعل المتزلج A في اتجاه مكان الانطلاق؛ لذا سيكون المتزلج B أقرب إلى مكان الانطلاق من المتزلج A. تحقق من فهمك (2) التزلج على الجليد : انطلقت مجموعتان من المتزلجين من المكان نفسه، فقطعت المجموعة A مسافة 4mi في اتجاه الشرق، ثم انحرفت 70 في اتجاه الشمال الشرقي قاطعةً مسافة 3mi، وقطعت المجموعة B مسافة 4mi في اتجاه الغرب، ثم انحرفت 75 في اتجاه الشمال الغربي قاطعة 3mi، أي مجموعة كانت الأبعد عن مكان الانطلاق عند هذه اللحظة؟ وضح . إجابتك. الدرس - المتباينات في مثلثين 123 Ministry of Edu 2024-1446

إرشادات للدراسة استعمال حقائق إضافية عند إيجاد مدى القيم الممكنة للمتغير x ، قد تحتاج إلى استعمال إحدى الحقائق الآتية: . قياس أي زاوية في المثلث يكون أكبر من 0 وأقل من 180 دائما. . طول أي قطعة لإثبات أن الزاوية المحصورة في مثلث أكبر من الزاوية المحصورة في مثلث آخر ، استعمل عكس متباينة SAS في الحل. مثال 3 استعمال الجبر في العلاقات بين مثلثين جبر أوجد متباينة تمثل مدى القيم الممكنة لـ د. الخطوة 1 من الشكل نعلم أن: . JH = GH, EH = EH, JE > EG إذن، mLJHE > mZEHG 6x + 15 > 65 x > 8 1/ عکس متباينة SAS عوض حل بالنسبة لـ X G 9 65° E 11 (6x+15) H مستقيمة يكون أكبر الخطوة 2: استعمل حقيقة أن قياس أي زاوية في المثلث أقل من 180 لكتابة متباينة أخرى. من 0 دائما. 124 mLJHE < 180° 6x+15180 x < 27.5 عوض حل بالنسبة لـ X الخطوة 3 اكتب المتباينتين 27.5 x ,8 x في صورة متباينة مركّبة بالشكل 27.5 > x > . تحقق من فهمك (3) أوجد متباينة تمثل مدى القيم الممكنة لـ x . 47 50 55 68° 50 5x+2 إثبات العلاقات في مثلثين: يمكنك استعمال متباينة SAS وعكسها لإثبات صحة العلاقات في مثلثين. مثال 4 إثبات علاقات المثلث باستعمال متباينة SAS اكتب برهانا ذا عمودين. المعطيات AB = AD المطلوب : EB ED البرهان : المبررات العبارات (1) معطى AB = AD (1 2) خاصية الانعكاس AE = AE (2) (3) مسلّمة جمع قياسات الزوايا (4) تعريف المتباينة (5) متباينة SAS mZEAB=mZEAD+mZDAB (3 mZEAB > mZEAD (4 EB > ED (5) تحقق من فهمك 4) اكتب برهانا ذا عمودين. المعطيات: RQ = ST المطلوب : RS > TQ الفصل 4 العلاقات في المثلث B A D E R Q T S وزارة التعليم Ministry of Education 2024-1446

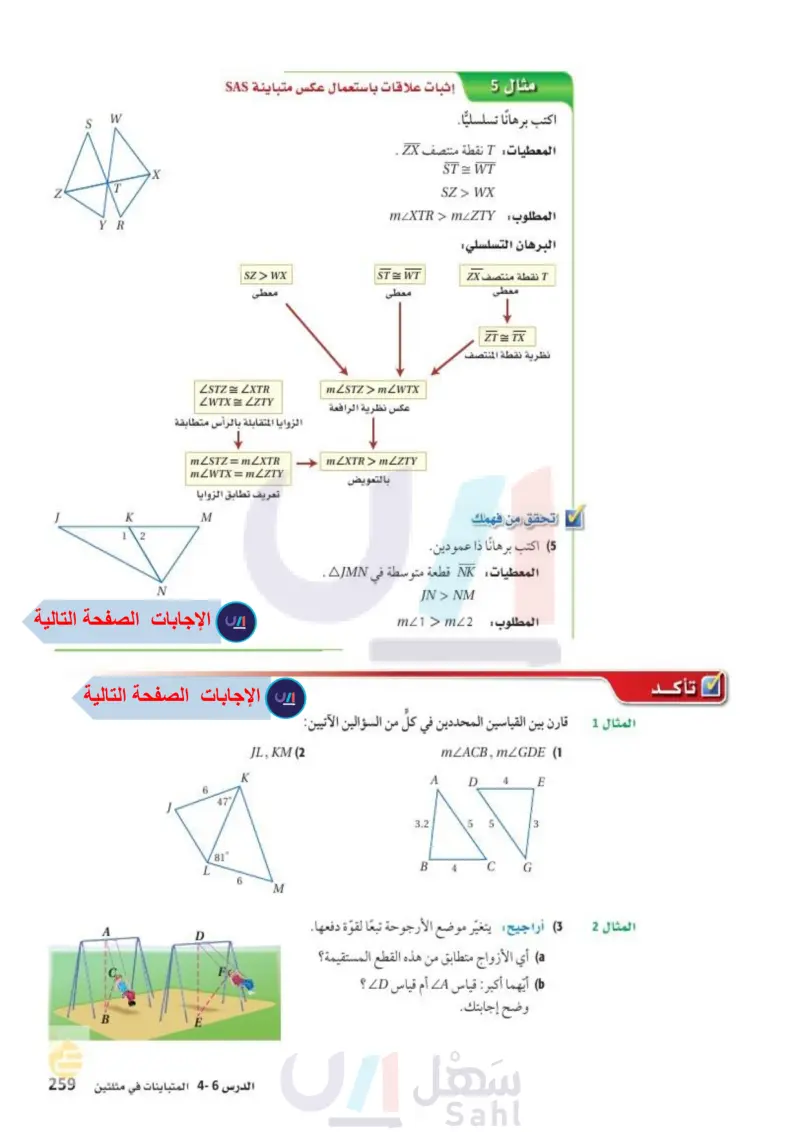
S W T Y R X N مثال 5 إثبات علاقات باستعمال عكس متباينة SAS اكتب برهانا تسلسلييًّا. المعطيات T نقطة منتصف ZX . ST = WT SZ > WX المطلوب : m_XTR > mzZTY البرهان التسلسلي SZ> WX ST = WT معطى LSTZ = LXTR ZWTX=ZZTY معطى mZSTZmZWTX عکس نظرية الرافعة الزوايا المتقابلة بالرأس متطابقة mLSTZ = mZXTR mZWTX = mZZTY mZXTR>mZZTY بالتعويض تعريف تطابق الزوايا M L, KM (2) K 6 47° /81° L 6 M الدرس - المتباينات في مثلثين ال125م Ministry of Edu 2024-1446 T نقطة منتصف ZX معطى ZT=TX نظرية نقطة المنتصف تحقق من فهمك (5) اكتب برهانا ذا عمودين. المعطيات NK قطعة متوسطة في AJMN . JN > NM m1> m2 المطلوب : المثال 1 قارن بين القياسين المحددين في كل من السؤالين الآتيين: mZACB, mZGDE (1 A D 4 E 3.2 5 5 3 B 4 C G المثال 2 (3) أراجيح يتغير موضع الأرجوحة تبعا لقوة دفعها. a أي الأزواج متطابق من هذه القطع المستقيمة؟ ) أيهما أكبر : قياس A أم قياس D ؟ وضح إجابتك.

3x-5/ 27% 37 2x + 3 المثال 3 اكتب متباينة تمثل مدى القيم الممكنة لـ تد في كل مما يأتي: (5 (4) 4 (2x-7)° 41° المثالان 4 برهان اكتب برهانا ذا عمودين في كل من السؤالين 67: (6) المعطيات AYZX YZ=XW المطلوب : ZX > YW (7) المعطيات: AD = CB DC <AB المطلوب : mZCBD < mLADB D C B X Y W Z تدرب وحل المسائل المثال 1 قارن بين القياسين المحددين في كل من الأسئلة الآتية: 10 38° PS, SR (10 ZTUW, ZVUW (9 10 P T 29° U 12 ZBAC, ZDGE (8 A 6 .B E 3. 4 5. C 3 W 11 V R S D 6 G المثال 2 11 رحلة برية : أقام باسم وعثمان مخيّما في الصحراء، وقرّرا أن يقوما برحلة برية، فانطلق باسم من المخيم وسار 5km في اتجاه الشرق، ثم انعطف 15 جهة الجنوب الشرقي وسار 2km أخرى، وانطلق عثمان من المخيم وسار 5km في اتجاه الغرب، ثم انعطف 35 جهة الشمال الغربي وسار 2km أخرى. a) أيهما أقرب إلى المخيم؟ وضح إجابتك، وارسم شكلًا توضيحيا. افترض أن عثمان انعطف 10% في اتجاه الجنوب الغربي بدلا من 35 في اتجاه الشمال الغربي، فأيهما يكون أبعد عن المخيم؟ وضح إجابتك، وارسم شكلًا توضيحيا. المثال 3 اكتب متباينة تمثل مدى القيم الممكنة لـ تد في كل من السؤالين الآتيين: وزارة التعليم Ministry of Education 2024-1446 ماجد 12 in. 17 in. 95° 5x+3 3x + 17 60° (13 57° 12 3.x 6, 41° (12 14) خزائن خزانتا سليم وماجد مفتوحتان كما في الشكل المجاور. أيُّ بابي الخزانتين يشكل زاوية قياسها أكبر ؟ وضح إجابتك. الفصل 4 العلاقات في المثلث 126

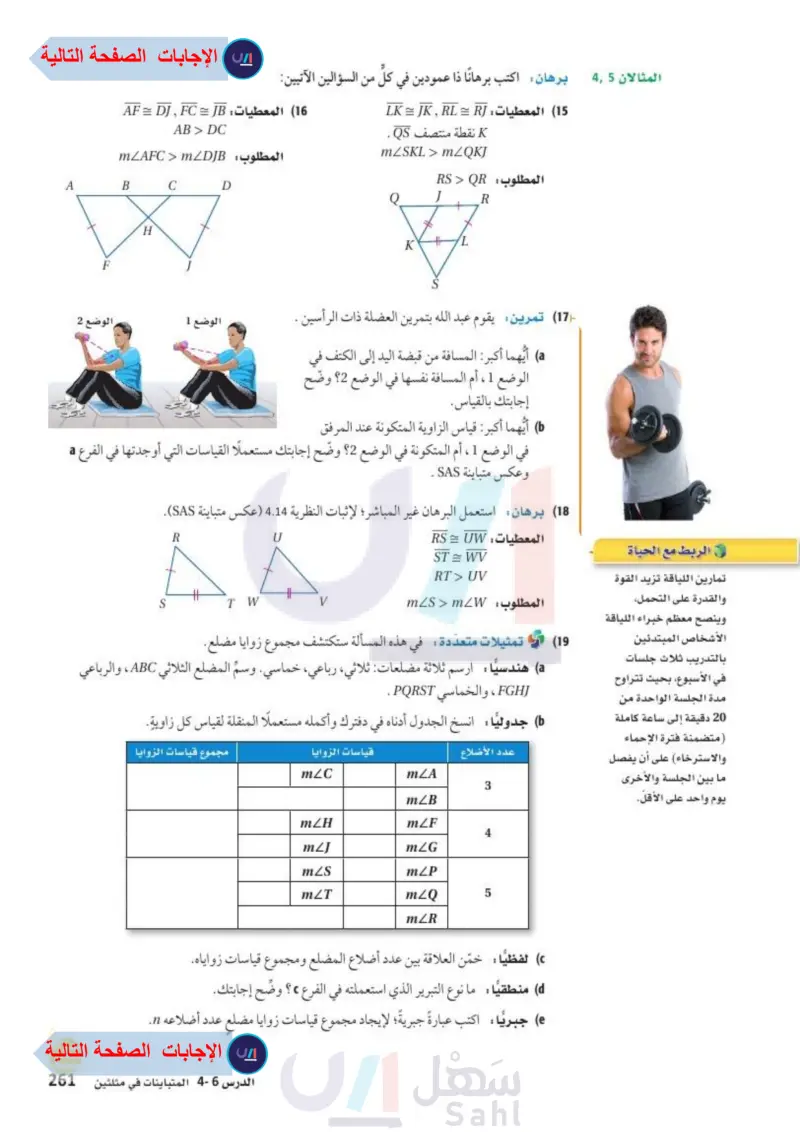
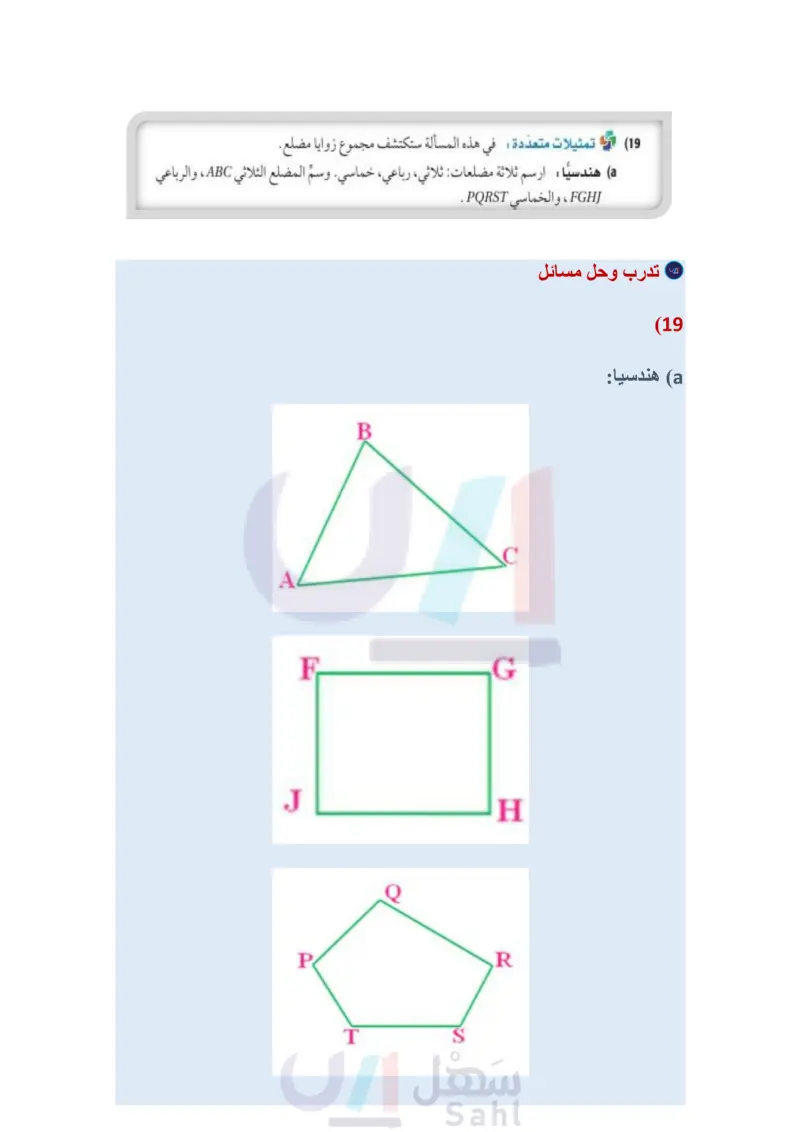
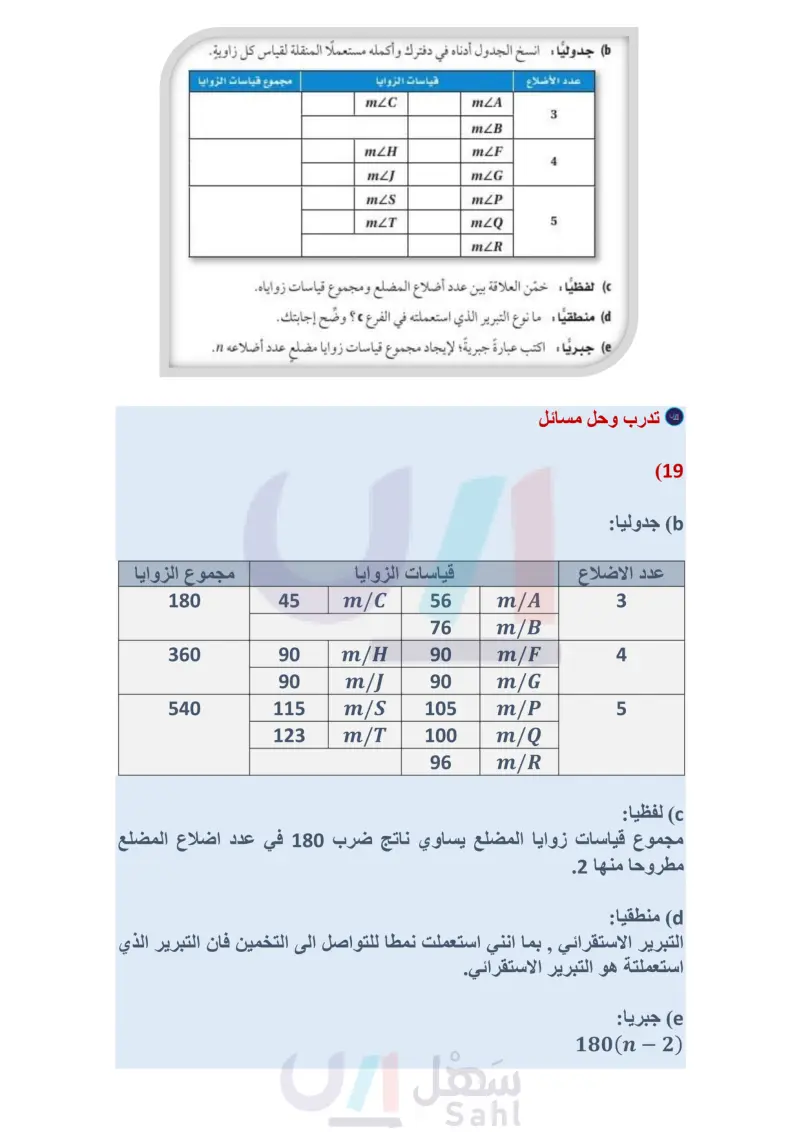
المثالان 4 برهان اكتب برهانا ذا عمودين في كلّ من ا الآتيين: (15) المعطيات LK = JK, RL = RJ نقطة منتصف QS . mZSKL> mZQKJ (16) المعطيات AF = DJ , FC = JB AB > DC المطلوب: mZAFC > mZDJB A B C D F H Q K S المطلوب : RSS QR R الربط مع الحياة تمارين اللياقة تزيد القوة والقدرة على التحمل وينصح معظم خبراء اللياقة الأشخاص المبتدئين بالتدريب ثلاث جلسات في الأسبوع، بحيث تتراوح مدة الجلسة الواحدة من 20 دقيقة إلى ساعة كاملة (متضمنة فترة الإحماء والاسترخاء) على أن يفصل ما بين الجلسة والأخرى يوم واحد على الأقل. (17) تمرين يقوم عبد الله بتمرين العضلة ذات الرأسين . a أيهما أكبر المسافة من قبضة اليد إلى الكتف في الوضع 1، أم المسافة نفسها في الوضع 2؟ وضح إجابتك بالقياس. ) أيهما أكبر قياس الزاوية المتكونة عند المرفق الوضع 1 الوضع 2 في الوضع 1، أم المتكونة في الوضع 2؟ وضح إجابتك مستعملا القياسات التي أوجدتها في الفرع a وعكس متباينة SAS . 18 برهان: استعمل البرهان غير المباشر ؛ لإثبات النظرية 4.13 (عكس متباينة SAS). المعطيات: RS = UW ST=WV RT> UV المطلوب ms > mW AA V T W (19) تمثيلات متعددة: في هذه المسألة ستكتشف مجموع زوايا مضلع. a) هندسيا ارسم ثلاثة مضلعات: ثلاثي، رباعي، خماسي. وسم المضلع الثلاثي ABC ، والرباعي FGH، والخماسي PQRST . جدوليا : انسخ الجدول أدناه في دفترك وأكمله مستعملا المنقلة لقياس كل زاوية. عدد الأضلاع قياسات الزوايا mZC مجموع قياسات الزوايا mZA 3 mZB mZH mZF 4 mZJ mZG mZS mZP mZT mZQ 5 mZR لفظيا خمّن العلاقة بين عدد أضلاع المضلع ومجموع قياسات زواياه. d) منطقيا ما نوع التبرير الذي استعملته في الفرع ، ؟ وضح إجابتك. جبريا: اكتب عبارةً جبرية؛ لإيجاد مجموع قياسات زوايا مضلع عدد أضلاعه n. الدرس - المتباينات في مثلثين ال127 Ministry of Edu 2024-1446

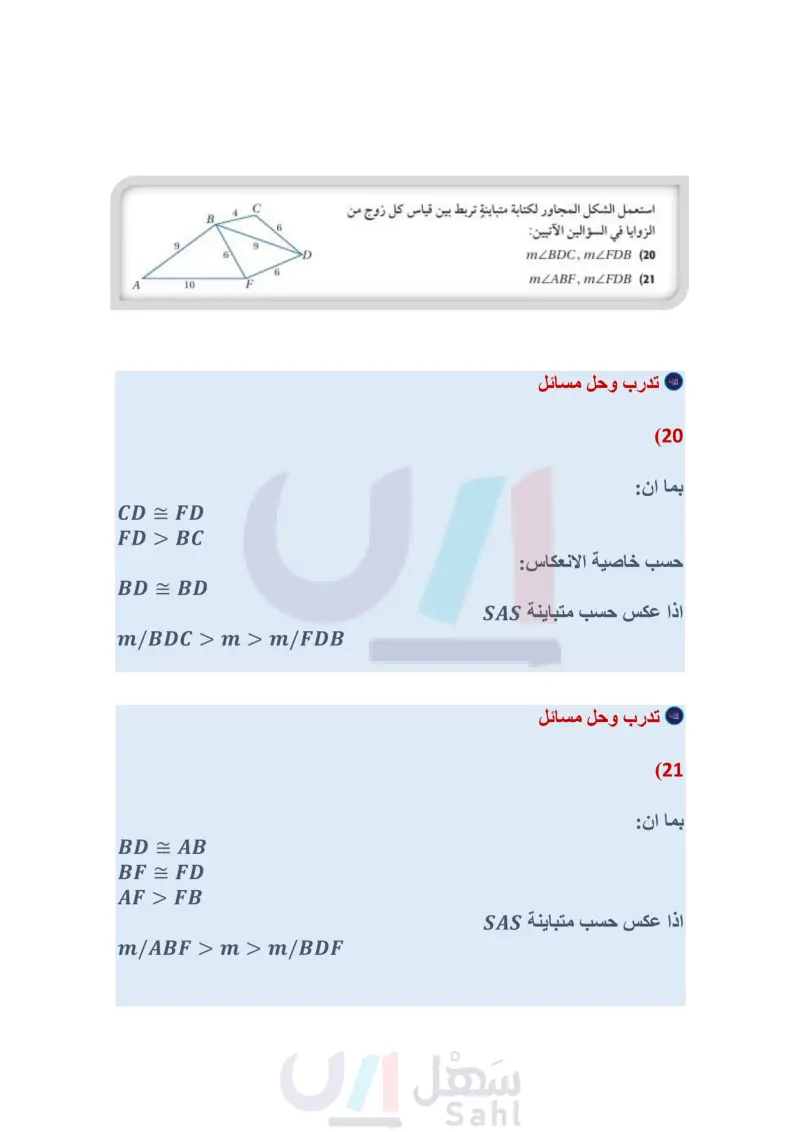
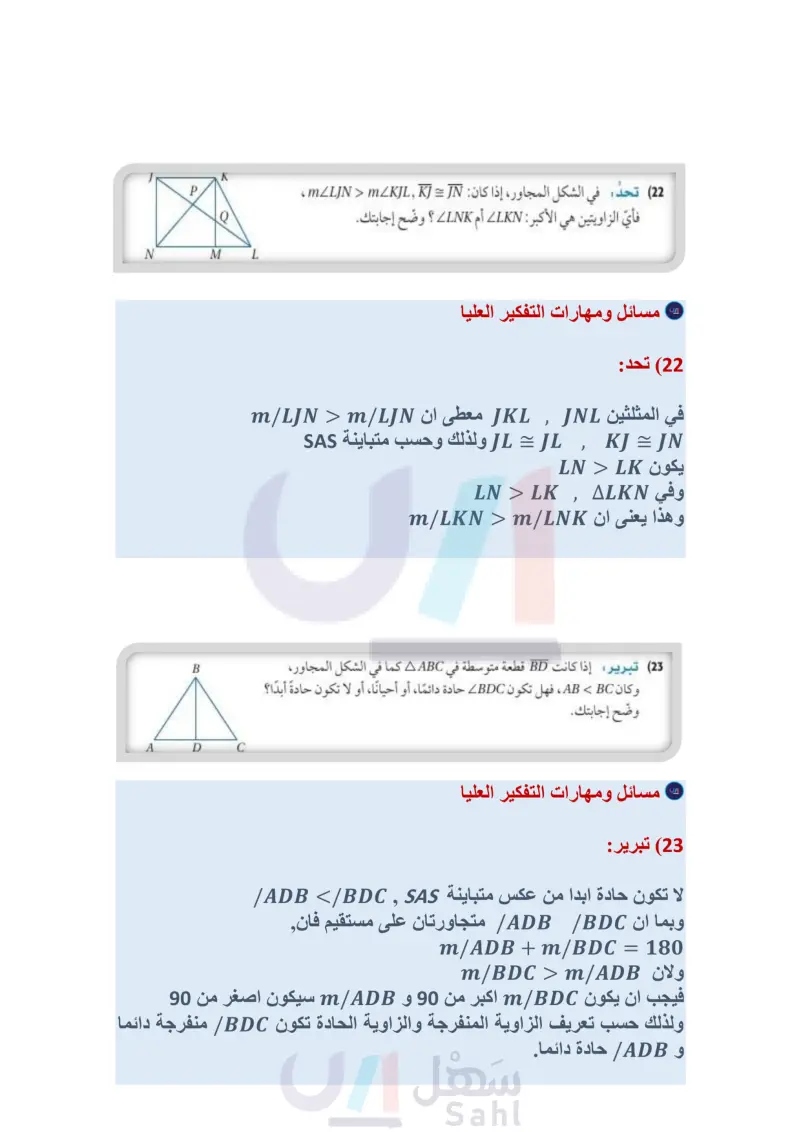
B 4 C 9 6 9 6 D 6 A 10 F N استعمل الشكل المجاور لكتابة متباينة تربط بين قياس كل زوج من الزوايا في السؤالين الآتيين: mZBDC, mZFDB (20 mZABF, mZFDB (21 مسائل مهارات التفكير العليا (22) تحد في الشكل المجاور، إذا كان mZLJN > mZKJL, KJ = IN ، فأي الزاويتين هي الأكبر : LKN أم LNK ؟ وضح إجابتك. (23) تبرير: إذا كانت BD قطعة متوسطة في AABC كما في الشكل المجاور، BC ، فهل تكون BDC حادة دائمًا، أو أحيانًا، أو لا تكون حادةً أبدًا؟ وكان AB P K 0 M L B A D C وزارة التعليم Ministry of Education 2024-1446 وضح إجابتك. تدريب على اختبار (24) اكتب بين أوجه الشبه وأوجه الاختلاف بين متباينة SAS والمسلّمة SAS لتطابق المثلثات. (25) أي متباينة مما يأتي تصف مدى القيم الممكنة لـ x ؟ ,(5r– 14)" 12 46° 12 26 إذا كان طول ضلع مربع +3+ x ، فإن طول قطره يساوي: 2x + 6 C x²√√2+6 D x2 + 1 A xV2 + 32 B 14 x>6 A 0 < x < 14 B 15 2.8 < x < 12 12 < x < 15 D مراجعة تراكمية اكتب متباينة تمثل مدى طول الضلع الثالث في مثلث عُلم طولا ضلعين من أضلاعه في كلّ من الأسئلة الآتية: (الدرس 5-4) 3.2 cm, 4.4 cm (27 5 ft, 10 ft (28 3 m, 9 m (29 30) رحلات سأل عليّ صديقه ماجدا عن تكلفة الرحلة التي قام بها مع صديقه، فلم يتذكر ماجد تكلفة الشخص الواحد، ولكنه تذكر أن التكلفة الكلية كانت أكثر من 500 ريال. استعمل البرهان غير المباشر لتبين أن تكلفة الشخص الواحد كانت أكثر من 250 ريالا. (الدرس 4-4) استعد للدرس اللاحق أوجد قيمة كل من x y في الأسئلة الآتية، موضحًا إجابتك : (33 (32 (4x)° (3y) (2y) 110° 72° 112° 78° (x+36) (2x + 24)° (2y-56) 115 الفصل 4 العلاقات في المثلث (31 128

الفصل 4 دليل الدراسة والمراجعة | ملخص الفصل المفاهيم الأساسية قطع مستقيمة خاصة في المثلثات : الدرسان -1- القطع المستقيمة الخاصة بالمثلثات هي الأعمدة المنصفة ومنصفات الزوايا والقطع المتوسطة والارتفاعات نقاط تقاطع المستقيمات الخاصّة في مثلث تُسمى نقاط التلاقي. نقاط التلاقي في مثلث هي مركز الدائرة الخارجية ومركز الدائرة الداخلية ومركز المثلث ومُلتقى الارتفاعات. البرهان غير المباشر: الدرس (44) كتابة برهان غير مباشر : (1) افترض أن النتيجة غير صحيحة. (2) بيّن أن هذا الافتراض يؤدي إلى تناقض (3) بما أن النتيجة الخطأ تؤدي إلى عبارة غير صحيحة، فإن النتيجة الأصلية ستكون صحيحة. متباينات المثلث : ( الدروس --- المفردات الأساسية العمود المنصف (ص 81) المستقيمات المتلاقية (ص (82) نقطة التلاقي ( ص (82) مركز الدائرة الخارجية للمثلث (ص (82) مركز الدائرة الداخلية للمثلث (ص 85) القطعة المتوسطة (ص 91) مركز المثلث (ص 91) ارتفاع المثلث (ص 93) ملتقى ارتفاعات المثلث (ص (93) التبرير غير المباشر (ص (107) البرهان غير المباشر (ص 107) البرهان بالتناقض (ص 107) اختبار المفردات بين ما إذا كانت كل جملة مما يأتي صحيحةً أو خاطئة، وإذا كانت . متباينة الزاوية الخارجية : قياس الزاوية الخارجية لمثلث خاطئة فاستبدل بالكلمة التي تحتها خط كلمة من القائمة أعلاه؛ لتجعل يكون أكبر من أي من الزاويتين الداخليتين البعيدتين عنها. الزاوية الكبرى في مثلث تقابل الضلع الأطول، والزاوية الصغرى تقابل الضلع الأقصر. الجملة صحيحة: 1) مركز المثلث هو النقطة التي تتقاطع عندها الارتفاعات . . مجموع طولي أي ضلعين في مثلث يكون أكبر من طول الضلع (2) نقطة تلاقي القطع المتوسطة لمثلث تُسمى مركز الدائرة الداخلية. 3) نقطة التلاقي هي النقطة التي تتقاطع عندها ثلاثة خطوط أو • المتباينة SAS (نظرية الرافعة إذا طابق ضلعان في مثلث الثالث. ضلعين مناظرين في مثلث آخر، وكان قياس الزاوية المحصورة في المثلث الأول أكبر من قياس الزاوية المحصورة في المثلث (4) مركز الدائرة الخارجية لمثلث يكون على أبعاد متساوية من رؤوس الثاني، فإن الضلع الثالث في المثلث الأول يكون أطول من الضلع الثالث في المثلث الثاني . المتباينة SSS: عكس نظرية (الرافعة إذا طابق ضلعان في مثلث ضلعين مناظرين في مثلث آخر، وكان الضلع الثالث في المثلث. 5) لإيجاد مركز المثلث، ارسم منصفات الزوايا أولا. المثلث الأول أطول من الضلع الثالث في المثلث الثاني، فإن 6 لتبدأ برهانا بالتناقض، أولا افترض أنّ ما تحاول أن تُثبته صحيح. قياس الزاوية المحصورة في المثلث الأول يكون أكبر من قياس الزاوية المحصورة في المثلث الثاني المطويات | منظم أفكار تأكد من أن المفاهيم الأساسية قد دونت في مطويتك. (7) يستعمل البرهان بالتناقض التبرير غير المباشر. 8) القطعة المتوسطة لمثلث تصل نقطة منتصف ضلع المثلث بمنتصف ضلع آخر للمثلث. 9) مركز الدائرة الداخلية لمثلث هو نقطة تتقاطع عندها منصفات زوايا المثلث. الفصل 4 دليل الدراسة والمراجعة 129 Ministry of Educe 2024-1446

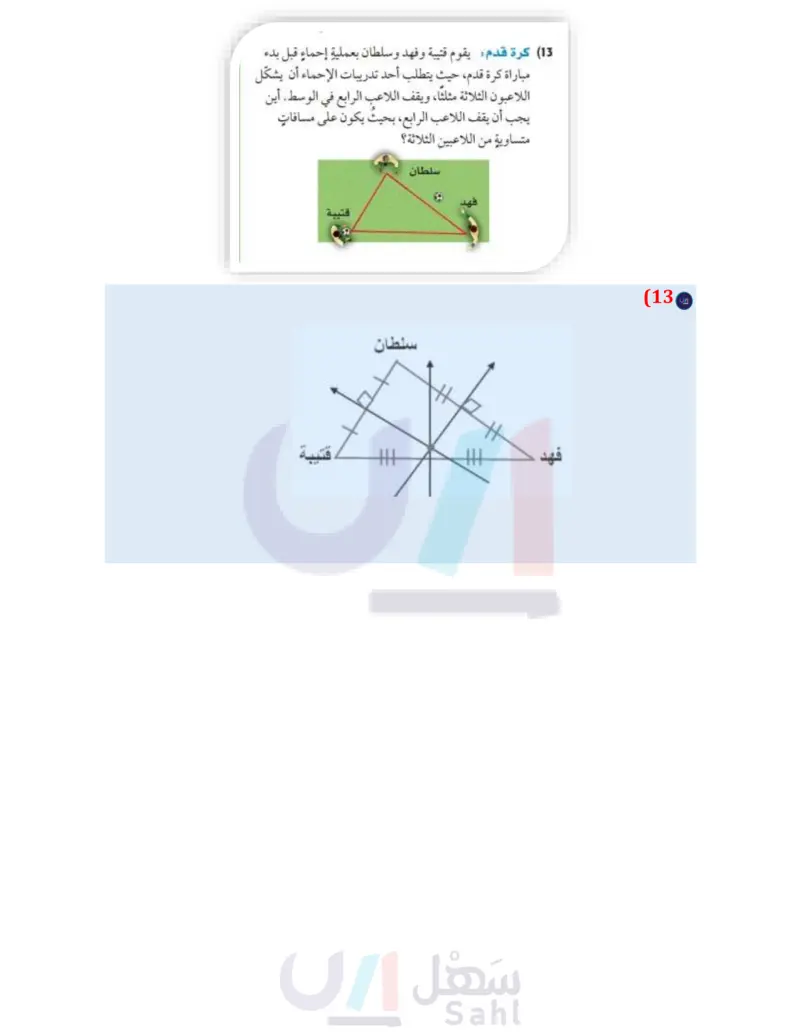
دليل الدراسة والمراجعة مثال 1 إذا كانت Q مركز الدائرة الداخلية لـ AJKL ، فأوجد كلا من القياسين الآتيين: L 25 PA AM 20 0 28° 25 N K mZQJK (a 180° = mKLP + MKN + mZNJP نظرية مجموع قياسات زوايا المثلث 2(25°)+2(28°) + mZNJP = 180° الفصل 4 مراجعة الدروس 4-1 المنصفات في المثلث (ص 81-89) 10 أوجد EG إذا كانت G مركز الدائرة الداخلية في AABC . أوجد كل قياس مما يأتي : B F E H 12 G 13 A XZ (12 R 5y-6 4.5 T RS (11 X 18 + 2y 106° + mZNJP = 180° mZNJP = 74° بسط اطرح 106 من الطرفين (13) كرة قدم: يقوم قتيبة وفهد وسلطان بعملية إحماء قبل بدء مباراة كرة قدم، حيث يتطلب أحد تدريبات الإحماء أن يشكل وبما أن IQ ينصف NJP ، إذن 2mQJK = mZNJP؛ أي أن | اللاعبون الثلاثة مثلثاً، ويقف اللاعب الرابع في الوسط. أين mZQJK = } mZNJP؛ إذن: °37 = °74 × { = mZQJK. يجب أن يقف اللاعب الرابع، بحيث يكون على مسافات متساوية من اللاعبين الثلاثة؟ QP (b وزارة التعليم Ministry of Education 2024-1446 نظرية فيثاغورس عوض 202 400, 252 = 625 اطرح 400 من الطرفين بسط a² + b² = c² (QP)2 + 202 = 25 2 (QP)2 + 400 = 625 (QP)2=225 QP = 15 12/ T 0 #+ قتيبة R سلطان فهد القطع المتوسطة والارتفاعات في المثلث (ص 91-98) مثال 2 4-2 14 رؤوس DEF هي (0 ,0 ,0 ,0). أوجد إحداثيات ملتقى ارتفاعات ADEF . إذا كانت النقطة T مركز المثلث EDF ، 15 احتفالات تُريد حفصة أن تعلّق 4 مثلثات متطابقة في 12 = FT ، فأوجد TQ سقف غرفة الصف، بحيث تكون موازية لأرضية الغرفة. فرسمت نموذجا لأحد المثلثات على مستوى إحداثي، FT= FT = 12 FT = = 3 (FT + TQ) 12 = (12 + TQ) (0, 4), (3, 8), (6,0) فكانت إحداثيات رؤوسه هي ) إذا كان كل مثلث سيُعلق في السقف بخيط، فما إحداثيات النقطة التي سيُربط الخيط عندها بالمثلث؟ D خاصية التوزيع اطرح 8 من الطرفين اضرب الطرفين في 12 = 8 + TQ 4 = 23/3TQ 6 = TQ الفصل 4 العلاقات في المثلث 130

4-3 المتباينات في المثلث (ص 99-105) اكتب زوايا كل مثلث مرتبةً من الأصغر إلى الأكبر في السؤالين الآتيين: مثال 3 اكتب زوايا AABC ، مرتبةً من الأصغر إلى الأكبر. 46° A B 74° C N (17) T (16) M (14x) (9x-10) 5 R (10x+5)° L 6 7 S 18 جيران يسكن سمير ومحمد وسامر عند تقاطعات ثلاثة شوارع تشكل المثلث المبين أدناه، إذا أرادوا الالتقاء عند أحدهم، فأي الطريقين أقصر : اصطحاب سمير لمحمد وذهابهما معًا إلى بيت سامر . أم اصطحاب محمد السامر وذهابهما معا إلى بيت سمير ؟ a أولا أوجد قياس الزاوية المجهولة باستعمال نظرية مجموع قياسات الزوايا. °60 = °74 + °46) - °180 = mLC لذا فالزوايا مرتبةً من الأصغر إلى الأكبر هي : AB والأضلاع مرتبة من الأقصر إلى الأطول هي: BC, AB, AC سامر 53° سمير 4-4 البرهان غير المباشر (ص 107-113) مثال 4 اكتب الافتراض الضروري الذي تبدأ به برهانا غير مباشر لكل عبارة مما يأتي: mZA≥ mZB (19 . AFGH = AMNO (20) اكتب الافتراض الضروري للبدء في برهان غير مباشر لكل عبارة مما يأتي: XYJK (a 21) KM قائم الزاوية. (22) إذا كان 12 > 3 ، فإن 4 > y . 23) اكتب برهانا غير مباشر لتبين أنه إذا كانت الزاويتان متتامتين، فإنه لا يمكن أن تكون أي منهما قائمة. الافتراض هو : XY = JK إذا كان 18 > x 3 ، فإن 6 > x نتيجة هذه العبارة الشرطية هي: 6 x ، ونفيها هو 6 x ؛ لذا فالافتراض هو 26 x (24) مطالعة اشترى محمود كتابين بأكثر من 180 ريالا، استعمل 2 زاوية حادة. البرهان غير المباشر لتبين أن ثمن أحدهما على الأقل أكثر من 90 ريالًا. الافتراض هو : 2 ليست زاوية حادة. الفصل 4 دليل الدراسة والمراجعة ال131 Ministry of Educe 2024-1446

وزارة التعليم Ministry of Education 2024-1446 دليل الدراسة والمراجعة الفصل 4 متباينة المثلث (ص 115-120 4-5 حدد ما إذا كانت القياسات المعطاة يمكن أن تمثل أطوال أضلاع مثال 5 مثلث في كل مما يأتي أم لا، وإذا لم يكن ذلك ممكنا، فوضح السبب. حدد ما إذا كانت القياسات (7) يمكن أن تمثل أطوال 5,6,9 (25 3, 4, 8 (26 أضلاع مثلث أم لا، وإذا لم يكن ذلك ممكنا، فوضح السبب. اكتب متباينة تمثل مدى طول الضلع الثالث في مثلث علم طولا اختبر كل متباينة. ضلعين من أضلاعه في كل من السؤالين الآتيين: 5ft, 7ft (27 10.5 cm, 4 cm (28 (29) دراجات يركب خالد دراجته لزيارة صديقه وليد، وبما أن 10+97 7+9 10 7+ 10 >9 197 16 10 179 الطريق المباشر مغلق، فقد سلك طريقا فرعيا طوله 2km ، ثم بما أن مجموع طولي أي ضلعين أكبر من طول الضلع الثالث، إذن القطع المستقيمة التي أطوالها 10 تشكل مثلثا . انعطف وسلك طريقًا آخر طوله km 3 حتى وصل منزل وليد. إذا كانت الطرق الثلاثة تشكل مثلثا رأسان من رؤوسه هما منزِلَا وليد وخالد ، فاكتب متباينةً تمثل مدى المسافة الممكنة بين منزليهما. 4-6 المتباينات في مثلثين (ص (121-128 (30) مستعملا المثلثين المجاورين قارن بين القياسين مثال 6 قارن بين كل قياسين فيما يأتي : C 3 B 3 E RQ, ST (a 5 D. 3 بما أن: RS = TQ, QS = QS, mLSQT > MLRSQ في المثلثين STORS إذن ، RQ < ST بحسب نظرية المفصلة. R Q 36" /31° T mZKML, mZKMJ (b بما أن : JM = LM, KM = KM K JK إذن (KML > KM . بحسب عكس نظرية المفصلة. 4 K M 4.8 L 3 2 A F mZABC, mZDEF 31) تجديف: يُجدف كل من رضوان وكمال في بركة متجهين إلى نقطة محددة، ولأنه ليس لهما خبرة في التجديف فقد انحرفا عن المسار مدة 4 دقائق، قطع كل منهما فيها مسافة 50m ، ثم استعادا مسارهما الصحيح، كما في الشكل. أيهما أقرب إلى نقطة النهاية عند هذه اللحظة ؟ كمال 50° 30° رضوان نقطة النهاية الفصل 4 العلاقات في المثلث 132

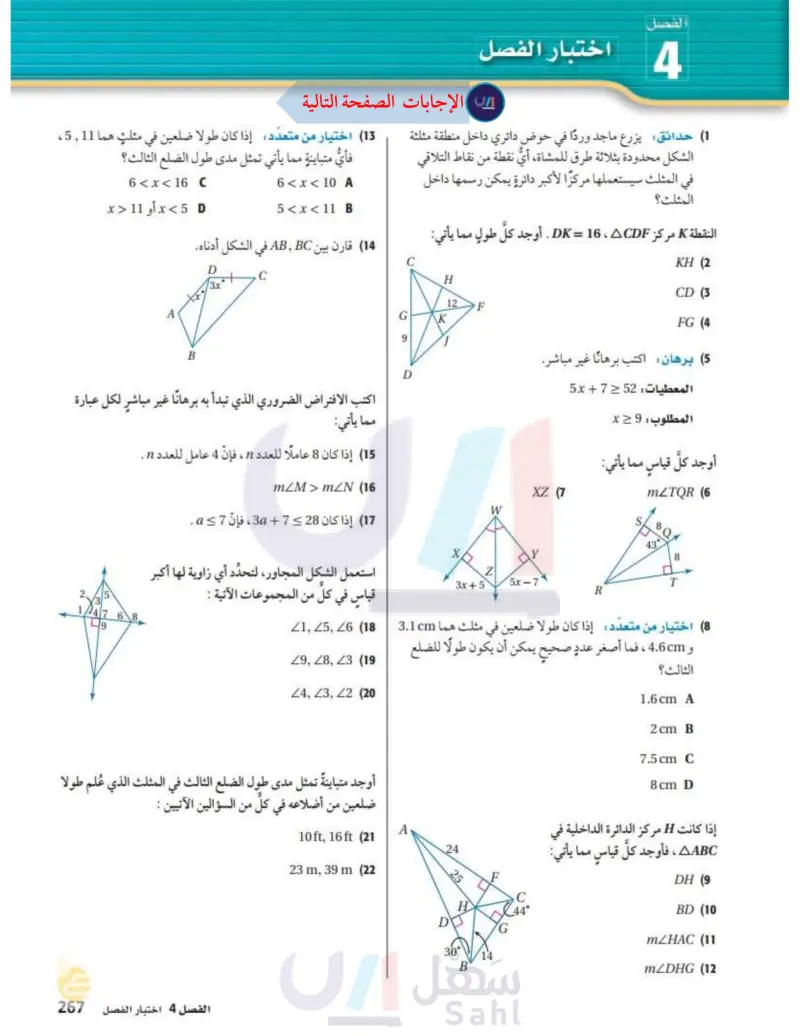
لفصل 4 اختبار الفصل 1) حدائق يزرع ماجد وردّا في حوض دائري داخل منطقة مثلثة (13) اختيار من متعدد: إذا كان طولا ضلعين في مثلث هما 511 الشكل محدودة بثلاثة طرق للمشاة نقطة من نقاط التلاقي في المثلث سيستعملها مركزا لأكبر دائرة يمكن رسمها داخل المثلث؟ النقطة K مركز DK = 16 ، ACDF . أوجد كل طول مما يأتي: فأي متباينة مما يأتي تمثل مدى طول الضلع الثالث؟ 6 < x < 10 A 5 < x < 11 B 6 < x < 16 x < 5 D أو 11 < x (14) قارن بين ABB في الشكل أدناه. A B D 73x C اكتب الافتراض الضروري الذي تبدأ به برهانا غير مباشر لكل عبارة مما يأتي: 15) إذا كان 8 عاملًا للعدد n ، فإن 4 عامل للعدد n . C H 12 F G K 9 D KH (2 CD (3 FG (4 (5) برهان اكتب برهانا غير مباشر المعطيات: 52 7 + 5x المطلوب : 9 = x أوجد كل قياس مما يأتي: mZM> mZN (16 XZ (7 W (17) إذا كان 28 7 + 3 ، فإنّ 7 = a . استعمل الشكل المجاور، لتحدد أي زاوية لها أكبر في كل من المجموعات الآتية : Z1, 25, 26 (18 Z9, 28, Z3 (19 Z4, Z3, Z2 (20 أوجد متباينةً تمثل مدى طول الضلع الثالث في المثلث الذي علم طولا ضلعين من أضلاعه في كل من السؤالين الآتيين : الفصل 4 اختبار الفصلا ال133 Ministry of Edu 2024-1446 mZTQR (6 43° Y Z 3x+5 5x-7 T R اختيار من متعدد: إذا كان طولا ضلعين في مثلث هما cm 3.1 و cm 4.6 ، فما أصغر عددٍ صحيح يمكن أن يكون طولًا للضلع الثالث؟ A 10ft, 16ft (21 24 23 m, 39 m (22 H DJJ 30° B F G 44° 1.6 cm A 2 cm B 7.5 cm C 8 cm D إذا كانت H مركز الدائرة الداخلية في AABC ، فأوجد كل قياس مما يأتي: DH (9 BD (10 mZHAC (11 mZDHG (12

الفصل الإعداد للاختبارات 4 استبعاد البدائل غير المعقولة يمكنك استبعاد البدائل غير المعقولة؛ لتحدّد الإجابة الصحيحة عند حل أسئلة الاختيار من متعدّد. طرائق استبعاد البدائل غير المعقولة الخطوة 1 اقرأ نَصَّ السؤال بعناية؛ لتحدّد المطلوب إيجاده بالضبط. ما المطلوب حله؟ • . هل الجواب عدد صحيح أم كسر اعتيادي أم كسر عشري؟ هل تحتاج إلى استعمال رسم أو جدول ؟ . ما وحدات القياس المطلوبة للإجابة (إن وجدت)؟ الخطوة 2 تفحص كل بديل بعناية وقدر معقوليته. استبعد أي بديل يبدو أنه غير صحيح. . استبعد أي بديل ليس ضمن الصيغة المناسبة للإجابة الصحيحة. استبعد أي بديل لا يتضمن وحدات القياس الصحيحة. الخطوة 3 حل السؤال، واختر الإجابة الصحيحة من بين البدائل المتبقية، ثم تحقق من إجابتك. مثال اقرأ المسألة، وحدّد المطلوب، ثم استعمل المعطيات في حلها. 134 ما قياس KLM ؟ 32° A 44° B 78° C 94° D الفصل 4 العلاقات في المثلث M (6x+8)° (9x-4)° K وزارة التعليم Ministry of Education 2024-1446

اقرأ السؤال وادرس الشكل بعناية. المثلث KLM قائم الزاوية. وبما أن مجموع قياسات الزوايا الداخلية لأي مثلث يساوي 180 ، فإن mKLM + mLMK يجب أن يساوي 90 ، وإلا زاد المجموع على 180 ، وبما أن البديل D هو قياس لزاوية منفرجة، فإنّه يُستبعد لعدم معقوليته؛ وعليه فالجواب الصحيح يكون A أو B أو C . حل المسألة. بحسب عکس نظرية منصف الزاوية التي تنص على أنه : "إذا وقعت نقطة داخل زاوية، وكانت على بعدين متساويين من ضلعيها، فإنّ هذه النقطة تقع على منصف الزاوية ، وبما أنّ النقطة M على بعدين متساويين من ضلعي الزاوية ، فإنّها تقع على منصف ILK ؛ لذا LILM يجب أن تطابق KLM ؛ والآن اكتب معادلة لإيجاد قيمة تد وحلها. 6x + 8 = 9 x 4 -3x=-12 x=4 إذن 32 = 4 - (4)] = KLM ، والبديل A يمثل الإجابة الصحيحة. تمارين ومسائل اقرأ كل سؤال فيما يأتي، ثم اكتب رمز الإجابة الصحيحة: 1 النقطة P مركز المثلث QUS ، إذا كان QP = 14 cm ، (3) ما إحداثيات ملتقى ارتفاعات المثلث أدناه ؟ У R V P (1,5) c (1, 1) D (-1,-1) A (-1, 1) S B 18 cm C 21 cm D فما طول QT ؟ 7 cm A 12 cm B (2) كم وحدةً مربعةً مساحة المثلث . في الشكل أدناه؟ إذا كان AABC متطابق الضلعين، وكان 94 = mLA ، فأي مما يأتي يجب ، أن تكون صحيحة ؟ mZB=94° A (0,7) mZB = 47° B AB = BC C AB = AC D y (9,0)* أي مما يأتي يمكن أن تكون أطوال أضلاع مثلث قائم الزاوية؟ 31.5 C 3, 7.2, 7.5 C 1.9, 3.2, 4 A 63D 2.6, 4.5, 6 D 1.6, 3, 3.4 B الفصل 4 الإعر135 Ministry of Educo 2024-1446 8A 27.4 B

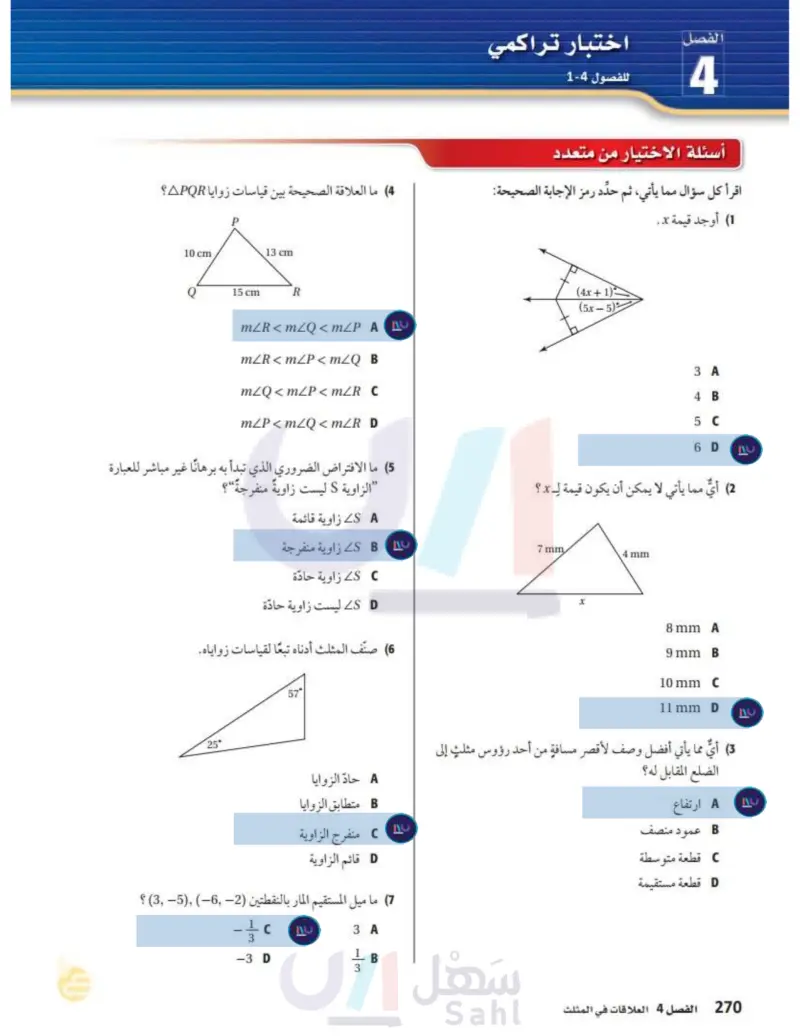
وزارة التعليم Ministry of Education 2024-1446 اختبار تراكمي للفصول 4-1 الفصل 4 أسئلة الاختيار من متعدد اقرأ كل سؤال مما يأتي، ثم حدد رمز الإجابة الصحيحة: (1) أوجد قيمة x . (4) ما العلاقة الصحيحة بين قياسات زوايا APQR؟ 10 cm 13 cm Q 15 cm R mZR<mZQ<mZP A (4x+1) (5x – 5) mZR<mZP<mZQ B mZQ<mZP<mZR C mZP<mZQ<mZR D 3 A 4 B 5 C 6 D (2) أي مما يأتي لا يمكن أن يكون قيمة لـ x ؟ (5) ما الافتراض الضروري الذي تبدأ به برهانا غير مباشر للعبارة الزاوية ليست زاوية منفرجة؟ SA زاوية قائمة SB زاوية منفرجة SC زاوية حادة SD ليست زاوية حادة (6) صنف المثلث أدناه تبعا لقياسات زواياه. 25° 57° 7 mm 4mm 8 mm A 9 mm B 10 mm C 11 mm D (3) أي مما يأتي أفضل وصف لأقصر مسافةٍ من أحد رؤوس مثلث إلى الضلع المقابل له؟ A ارتفاع B عمود منصف C قطعة متوسطة D قطعة مستقيمة حاد الزوايا متطابق الزوايا منفرج الزاوية قائم الزاوية الفصل 4 العلاقات في المثلث 136

أسئلة ذات إجابات قصيرة أجب عن الأسئلة الآتية: (7) إذا كان طولا ضلعين في مثلث هما cm 15cm 9 ، فما أصغر عدد صحيح من السنتمترات يمكن أن يكون طولا للضلع الثالث؟ 8 ما إحداثيات ملتقى ارتفاعات المثلث أدناه ؟ 11) خرج كل من حمزة وهاني مع فرقة الكشافة وخيموا في الصحراء، فترك حمزة المخيم وسار 2km في اتجاه الشرق. ثم انعطف °20 في اتجاه الجنوب الشرقي. وسار 4km أخرى. وأما هاني فسار 2km في اتجاه الغرب، ثم انعطف °30 في اتجاه الشمال الغربي ، وسار 4km أخرى. أيهما أبعد عن المخيم؟ (12) أوجد قيمة x في المثلث أدناه. (3x+25) (4x+5)° (5x − 30)° أسئلة ذات إجابات مطولة +A(−3, 1), B(0, 2), C(3,4) * AABC 99,255 3) (13 فأجب عن الأسئلة التالية مبينا خطوات الحل : a ارسم هذا المثلث في المستوى الإحداثي. أوجد أطوال أضلاعه (قرب إلى أقرب جزء من عشرة). صنفِ المثلث من حيث أضلاعه وزواياه. d قارن بين mam 0 9) اكتب أضلاع المثلث أدناه مرتبة تبعا لأطوالها من الأقصر R /56° 61 S x+5, 13 12 11 10 9 8 7 6 3 2 1 3-1, 3-2 4-6 4-6 4-2 4-3 3-1 4-5 4-4 4-2 4-3 4-5 4-1 4-3 الفصل 4 اختبار تراكم ال 137 Ministry of Educ 2024-1446 إلى الأطول (10) اكتب متباينة تصف قيم x الممكنة. 45° 3x 7 هل تحتاج إلى مساعدة إضافية ؟ إذا لم تستطع الإجابة عن ... فعد إلى الدرس...