الدوال الأسية - رياضيات1-3 - ثالث ثانوي
الفصل الأول: تحليل الدوال
الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
نشاط الفصل الأول: تحليل الدوال
نشاط الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
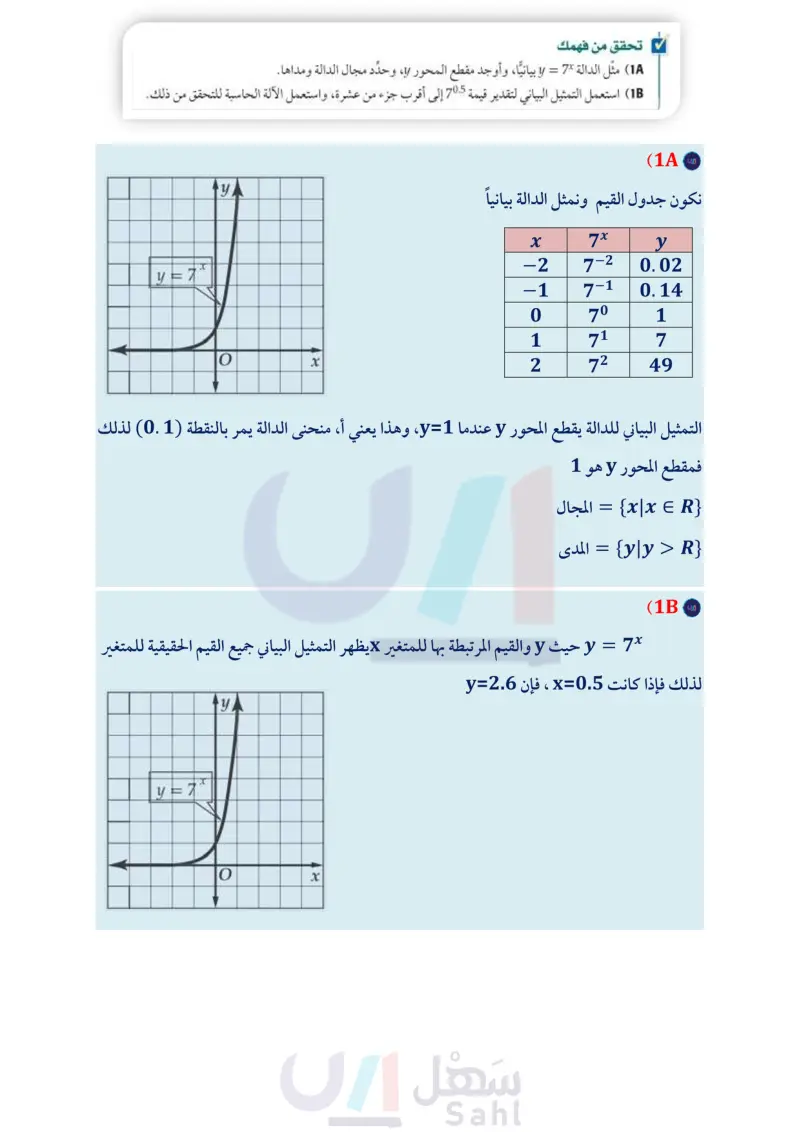
عدد العناكب ) بالمئات) رابط الدرس الرقمي www.ien.edu.sa الدوال الأسية Exponential Functions 2-1 فيما سبق: درست دوال كثيرات الحدود لماذا؟ قد تبدو عناكب الرتيلاء Tarantulas) مخيفة بأجسامها الكبيرة المغطاة بالشعر وتمثيلها بيانيا. الدرس (11) وأرجلها الكبيرة ، ولكنها غير مؤذية للإنسان، ويبيّن التمثيل المجاور الزيادة في والآن : أتعرف الدالة الأسية أمثل الدالة الأسية. أمثل دوال النمو الأسي بيانيا. أمثل دوال الاضمحلال الأسى بيانيا. المفردات: الدالة الأسية exponential function النمو الأسى exponential growth عامل النمو أعدادها عبر الزمن. لاحظ أن هذا التمثيل ليس خطيًّا، وليس تربيعيا أيضًا، وإنما يمثل الدالة 32 = y ، والتي هي مثال على الدالة الأسية. * y، -35- 30 -25- -20- -15- -10- -5- 0 1 2 3 4 5 6x السنوات منذ 2010 تمثيل الدوال الأسية: الدالة الأسية هي دالة مكتوبة على الصورة y = ab حيث 1 , , a . + ± 0, b > 0, b لاحظ أن الأساس في الدالة الأسية ثابت، وأن الأس هو المتغير المستقل. مفهوم أساسي الدالة الأسية التعبير اللفظي : أمثلة : الدالة الأسية هي دالة يمكن وصفها بمعادلة على الصورة y = abx, a ± 0, b > 0, b ± 1 y = 4x y = (-1) x y = 2(3)x growth factor الاضمحلال الأسى exponential decay مثال 1 تمثيل الدالة الأسية عندما 0 < b > 1 ، a a مثل الدالة × 3 = y بيانيًّا، وأوجد مقطع المحور ، وحدد مجال الدالة ومداها. y عامل الاضمحلال decay factor إرشادات للدراسة الدالة y = abx : : تكون الدالة الأسية *y = ab معرفة لجميع قيم x التي تحقق الشرط a0,b>0, b 1 وذلك لأنه : . إذا كانت 0 > b فإن • y = ab x تكون غير معرفة عند بعض القيم فمثلا تكون غير معرفة عند c = } ، x= إذا كانت 1 = b فإن الدالة تصبح على الصورة الدالة y = a وهذه هي الثابتة. جميع x 3x -2 3-2 −1 3-1 V1913 У ㅎ 0 3º 1 1 31 3 2 32 9 X y= 3* هو عيّن الأزواج المرتبة الواردة في الجدول، ثم صل بينها بمنحنى. لاحظ أن التمثيل البياني للدالة يقطع المحور y عندما 1 = y ، وهذا ل ، وهذا يعني أن منحنى الدالة يمر بالنقطة (1 ) ، لذا فمقطع المحور ل هو 1، ومجال الدالة الأعداد الحقيقية، ومداها جميع الأعداد الحقيقية الموجبة. استعمل التمثيل البياني لتقدير قيمة 30.7 إلى أقرب جزء من عشرة. يظهر التمثيل البياني جميع القيم الحقيقية للمتغير x والقيم المرتبطة بها للمتغير ، حيث y = 3 x، لذا فإذا كانت 0.7 = x فإن 2.2 ، ، ، استعمل الآلة الحاسبة للتحقق من أن 2.157669 30.7) . تحقق من فهمك ~ 1A مثل الدالة y = 7x بيانيًّا، وأوجد مقطع المحور ، وحدد مجال الدالة ومداها. IB) استعمل التمثيل البياني لتقدير قيمة 70.5 إلى أقرب جزء من عشرة ، واستعمل الآلة الحاسبة للتحقق من ذلك. يتضح من المثال (1) أعلاه أنه كلما ازدادت قيم x بمقدار ثابت قيمته (1) فإن قيم لا تزداد أيضًا بنسبة ثابتة، فكل قيمة لـ لا تمثل 3 أمثال القيمة السابقة لها مباشرة، لذا فالدالة متزايدة، كما أن المحور x هو خط تقارب أفقي لها. وزارة التعليم Ministry of Education 2024-1446 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 80

إذا كانت b=1 فإن الدالة تصبح على الصورة y=a وهذه هي الدالة الثابتة.
المفردات لدرس الدوال الأسية
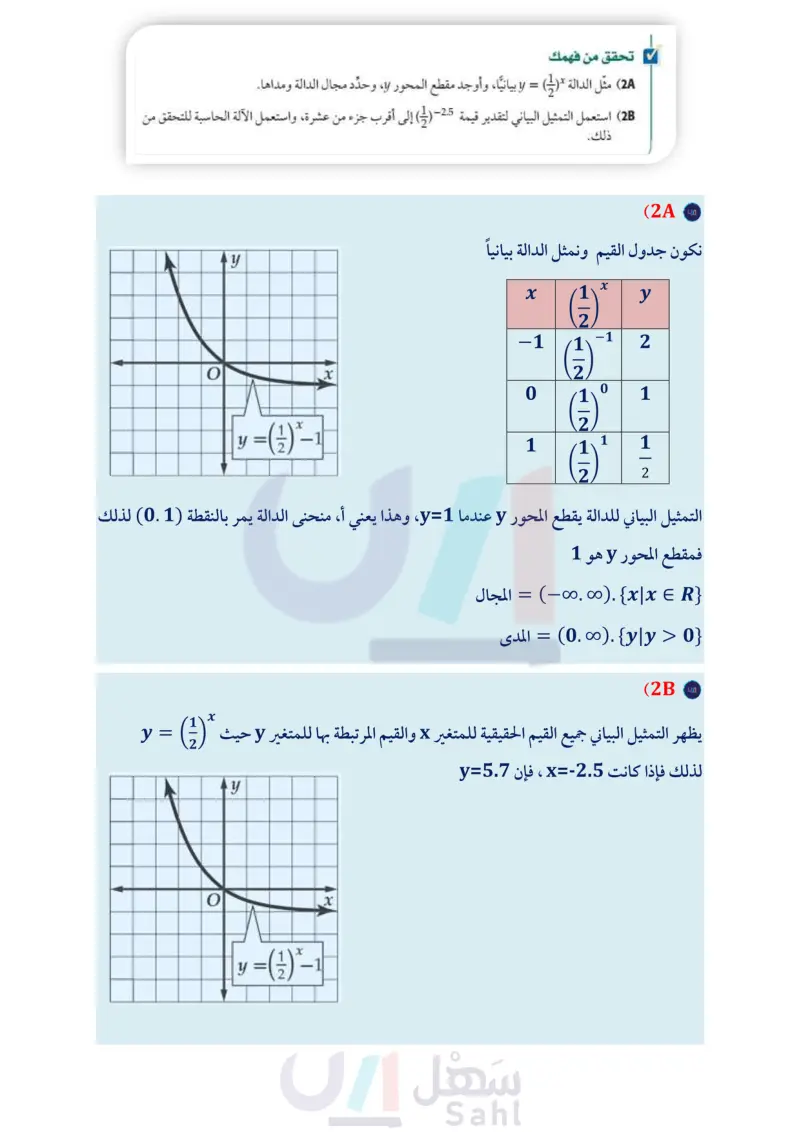
إرشادات للدراسة a < 0 إذا كانت قيمة a سالبة، فإن منحنى الدالة ينعكس حول المحور x . مثال 2 تمثيل الدالة الأسية عندما 0 < b< 1،a> 0 ( مثل الدالة " (3) = y بيانيا، وأوجد مقطع المحور y، وحدد مجال الدالة ومداها. y X x У | y = ( 31 ) * | -2 (1)-2 9 0 1 2 Of x (¹)² 19 عيّن الأزواج المرتبة الواردة في الجدول، ثم صل بينها بمنحنى. لاحظ أن التمثيل البياني للدالة يقطع المحور y عندما 1 = y، أي أن منحنى الدالة يمر بالنقطة (1, 0)، لذا فمقطع المحور لا هو 1، ومجال الدالة هو جميع الأعداد الحقيقية، ومداها جميع الأعداد الحقيقية الموجبة. استعمل التمثيل البياني لتقدير قيمة 1.5- (3) إلى أقرب جزء من عشرة. عندما 1.5 - = x، فإن قيمة 5.2 = y ، استعمل الآلة الحاسبة للتحقق من أن 5.19615 ~ ((¹)-1.55.19615 تحقق من فهمك 2A مثل الدالة * (3) = y بيانيا، وأوجد مقطع المحور y، وحدد مجال الدالة ومداها. 2B) استعمل التمثيل البياني لتقدير قيمة 2.5 - ( ) إلى أقرب جزء من عشرة، واستعمل الآلة الحاسبة للتحقق من ذلك. يتضح من المثال (2) أعلاه أنه كلما ازدادت قيم x بمقدار ثابت قيمته (2) فإن قيم لا تتناقص بنسبة ثابتة، فكل قيمة لـ لا تمثل القيمة السابقة لها مباشرة، لذا فالدالة متناقصة، كما أن المحور x هو خط تقارب أفقي لها. النمو الأسي: تسمى الدالة الأسية * f(x) = b ، حيث 1 دالة النمو الأسي، فالدالة 3 = y الواردة في المثال 1 هي دالة نمو أسي. مفهوم أساسي الدالة الرئيسة (الأم) لدوال النمو الأسي الدالة الرئيسة (الأم) : 1 < f(x) = bx, b خصائص منحنى الدالة : متصل متباين، متزايد المجال : المدى : خط التقارب : مقطع المحور y : النموذج : مجموعة الأعداد الحقيقية (R) مجموعة الأعداد الحقيقية الموجبة (R) المحور x 1 f(x) f(x) = bx, b>1 (-1, 1) (1, b) (0, 1) x يمكنك تمثيل دوال النمو الأسى بيانيًا بنفس طريقة تمثيل الدوال الأسية، كما يمكنك الاستفادة من النقاط : (−1, 1), (0, 1), (1, b) b وزارة التعليم الدرس 1-2 الدوال الأسية 81 2024-1446

إذا كانت قيمة a سالبة فإن منحنى الدالة ينعكس حول المحور x.
الربط مع الحياة تُعد الإحصاءات السكانية أحد أهم مصادر البيانات التي يتطلبها التخطيط التنموي في المجالات الاقتصادية والاجتماعية. وقد أجري أول تعداد سكاني في المملكة عام 1394 هـ ، وكان عدد سكان المملكة حينئذ 7 ملايين نسمة تقريبًا. تنبيه النسبة المئوية تذكر أن جميع أشكال النسب المئوية تتحول إلى كسور عشرية. فمثلا، 0.125 12.5% 6 لاحظ أن قيم (f(x تزداد كلما زادت قيم .. ولذلك نقول: إن (f(xدالة متزايدة. يمكنك تمثيل الزيادة في قيمة ما بنسبة مئوية ثابتة في فترات زمنية متساوية باستعمال دالة النمو الأسي ( 1 ) ، حيث t الفترة الزمنية، a القيمة (1) + a = (A (t الابتدائية ، r النسبة المئوية للنمو في الفترة الزمنية الواحدة. لاحظ أن أساس العبارة الأسية هو (1) + r) ويُسمى عامل النمو. وتستعمل دوال النمو الأسي عادةً لتمثيل النمو السكاني. X مثال 3 من واقع الحياة تمثيل دوال النمو الأسي بيانيًّا تعداد سكاني: بلغ المعدل السنوي للنمو السكاني في المملكة خلال الفترة 1431 - 1425 %3.2 تقريبًا. إذا كان عدد سكان المملكة 22678262 نسمة عام 1425هـ ، فأوجد معادلة أسية تمثل النمو السكاني للمملكة خلال هذه الفترة، ثم مثلها بيانيًا باستعمال الحاسبة البيانية. أوجد دالة النمو الأسي مستعملا 0.032 = a = 22678262, r y = 22678262 (1.032) مثل الدالة بيانيًا باستعمال الحاسبة البيانية TI-nspire لتحصل على الشكل المجاور. تحقق من فهمك : 43 1.1 -82-1 5.55E+7 y f1(x)=22678262 (1.032)* (3) ثقافة مالية يتوقع أن يزداد إنفاق عائلة بما نسبته 8.5% سنويًّا، إذا كان إنفاق العائلة عام 1430هـ هو 80000 ريال، فأوجد معادلة أسية تمثل إنفاق العائلة منذ عام 1430 ثم مثلها بيانيًا باستعمال الحاسبة البيانية. هي هـ ، الاضمحلال الأسي: تُسمى الدالة الأسية ) = (f(x ، حيث 1 > > 0 دالة الاضمحلال الأسي، فالدالة (3) = y الواردة في المثال 2 دالة اضمحلال أسي. مفهوم أساسي الدالة الرئيسة (الأم) لدوال الاضمحلال الأسي الدالة الرئيسة (الأم) : 1 > f(x) = b, 0 < b خصائص منحنى الدالة : متصل متباين متناقص مجموعة الأعداد الحقيقية (R) المجال : المدى : خط التقارب : النموذج : مجموعة الأعداد الحقيقية الموجبة (R) المحور x Af(x) f(x) = bx, 0 <b<1 (11) (1, b) (0, 1) 0 x مقطع المحور y : 1 الربط مع الحياة الشاي الأخضر قليل الأكسدة بخلاف الشاي الأسود، وقد أثبتت بعض الدراسات العلمية والطبية أن الذين يشربون الشاي الأخضر أقل عرضةً للإصابة بأمراض القلب وأنواع معينة من السرطان. يمكنك تمثيل دوال الاضمحلال الأسي بيانيًا بنفس طريقة تمثيل دوال النمو الأسي، ونلاحظ أن قيم (f(x تقل كلما زادت قيم x ، ولذلك نقول: إن (f(xدالة متناقصة. وكما في النمو الأسي، فإنه يمكنك تمثيل النقص في قيمة ما بنسبة مئوية ثابتة في فترات زمنية متساوية باستعمال دالة الاضمحلال الأسي ) (1) (t) ، حيث a القيمة الابتدائية ، r النسبة المئوية للاضمحلال في الفترة الزمنية الواحدة. لاحظ أن أساس العبارة الأسية هو (r) - (1)، ويُسمى عامل الاضمحلال. = 6 وتستعمل دوال الاضمحلال الأسي عادة في التطبيقات المالية. مثال 4 من واقع الحياة تمثيل دوال الاضمحلال الأسي بيانيا شاي: يحتوي كوب من الشاي الأخضر على 35mg من الكافايين، ويمكن للأشخاص اليافعين التخلص من %12.5 تقريبًا من كمية الكافايين من أجسامهم في الساعة. أوجد دالة أسية تمثل كمية الكافايين المتبقية في جسم اليافعين بعد شرب كوب من الشاي الأخضر، ثم مثلها بيانيا باستعمال الحاسبة البيانية. 1.1 *83-1 f1(x)=35 (0.875)* 50 y 82 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية ظهما التعليم Ministry of Education 2024-1446

تعد الإحصائيات السكانية أحد أهم مصادر البيانات التي يتطلبها التخطيط التنموي في المجالات الاقتصادية والاجتماعية .
النسبة المئوية تذكر أن جميع أشكال النسب المئوية تتحول إلى كسور عشرية
الشاي الاخضر قليل الأكسدة، بخلاف الشاي الأسود . وقد أثبتت بعض الدراسات العلمي والطبية أن الذين يشربون الشاي الأخضر أقل عرضة للإصابة بأمراض القلب وأنواع معينة مثل السرطان.
y = a(1 – r)t = 35(1 − 0.125)t = 35(0.875) لاحظ التمثيل البياني للدالة باستعمال الحاسبة البيانية. قدر كمية الكافايين المتبقية في جسم شخص يافع بعد 3 ساعات من شربه كوبًا من الشاي الأخضر . y = 35(0.875)t = 35(0.875)3 المعادلة من الفرع a عوض 3 بدلا من الزمن t استعمل الحاسبة ≈23.45 سيبقى في جسم تحقق من فهمك هذا الشخص 23.45mg من الكافايين تقريبًا بعد 3 ساعات. (4) يحتوي كوب من الشاي الأسود على 68mg من الكافايين. أوجد معادلة أسية تمثل كمية الكافايين المتبقية في جسم شخص يافع بعد شربه كوبًا من الشاي الأسود، ومثلها بيانيًا مستعملا الحاسبة البيانية، ثم قدّر كمية الكافايين المتبقية في جسمه بعد ساعتين من شربه الكوب. التحويلات الهندسية : تؤثر التحويلات الهندسية في شكل منحنى الدالة الرئيسة (الأم) لكلّ من دالتي النمو الأسي والاضمحلال الأسي كما هو الحال في باقي الدوال، وستقتصر دراستنا على بعض التحويلات الهندسية لهاتين الدالتين. مفهوم أساسي الانسحاب الرأسي والانسحاب الأفقي الانسحاب الرأسي الانسحاب الأفقي منحنی g(x) = f(x) + k هو انسحاب لمنحنى (f(x : منحنی ) - (g(x) = f(x هو انسحاب لمنحنى (f(x: • وحدة إلى أعلى عندما 0 < . || من الوحدات إلى أسفل عندما 0 > k . • من الوحدات إلى اليمين عندما 0 <h. || من الوحدات إلى اليسار عندما 0 > h . |y = f(x)| |g(x) = f(x + h) 0 y y |g(x)=f(x-h) x |g(x) = f(x) + k| G y = f(x) | |y = f(x) y = f(x) وزارة التعليم الدرس 1-2 الدوال الأسية 83 2024-1446 |g(x)=f(x)-k x X

y |g(x)= f(x) y=f(x) X مفهوم أساسي الانعكاس حول المحور لا منحنى الدالة ( x) = f ( x) هو انعكاس لمنحنى الدالة (f(x حول المحور لا . إرشادات للدراسة الاضمحلال الأسي: تأكد من عدم الخلط بين تضييق التمثيلات البيانية حيث 1>|a| . والاضمحلال الأسي، حيث 1>b> 0 مفهوم أساسي التمدد الرأسي إذا كان a عددًا حقيقيًا موجبًا، فإن منحنى الدالة ( x) = a f ( x) هو : توسع رأسي لمنحنى (f(x ، إذا كانت 1 < a . g(x) ) = a f(x), a > 1 تضيق رأسي لمنحنى (f(x ، إذا كانت 1 > a > 0 y y= f(x)| X g(x) = a f(x), 0<a<1 y = f(x)| x إرشادات للدراسة سلوك طرفي التمثيل البياني مجال الدالتين في المثال 5 هو مجموعة الأعداد الحقيقية (R). تذكر أن سلوك طرفي التمثيل البياني هو سلوك التمثيل البياني مع اقتراب x من مالانهاية أو سالب مالانهاية. نلاحظ في المثال (5a) أنه مع اقتراب x من مالانهاية، تقترب ل من مالانهاية أيضًا، وأما عندما تقترب x من سالب مالانهاية فإن لا تقترب من 1. وفي المثال (56) عندما تقترب x من مالانهاية فإن لا تقترب من سالب مالانهاية، وأما عندما تقترب x من سالب مالانهاية، فإن لا تقترب من الصفر. مثال 5 تحويلات التمثيلات البيانية لدوال النمو الأسي مثل كل دالة مما يأتي بيانيا، وحدد مجالها، ومداها: 4 = 2x + 1 (a حدد نقاط التمثيل البياني للدالة الأم 2 = y . بما أن 12 فالدالة دالة نمو أسي، لذا استعمل النقاط (1)، (1) ، ( 1 ) أي النقاط (1,2)، (0,1)، (1)، والتمثيل البياني للدالة هو تحويل للتمثيل البياني للدالة 2 = y، بما أن 1 = فإن المعادلة 1+2 = y تمثل انسحابا لمنحنى الدالة الرئيسة (الأم) y = 2x وحدة واحدة إلى أعلى. وبالاستعانة بالأزواج المرتبة الواردة في الجدول أيضًا، فإن التمثيل البياني للدالة 1 + 2 = y يكون كما هو موضح أدناه. 181412 x 21 y -3 2-3 +1 1층 -2 2-2 +1 1. 1 -1 2- +1 11 y = 20 0 20+1 2 1 21+1 3 2 22+1 LO 5 y=2x+1 y 8 7 19 6543 -4-3-2-10 1 2 3 x المجال هو مجموعة الأعداد الحقيقية (R) ، والمدى هو {1 < y | y} وزارة التعليم Ministry of Education 2024-1446 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 84

سلوك طرفي التمثيل البياني
الاضمحلال الأسي
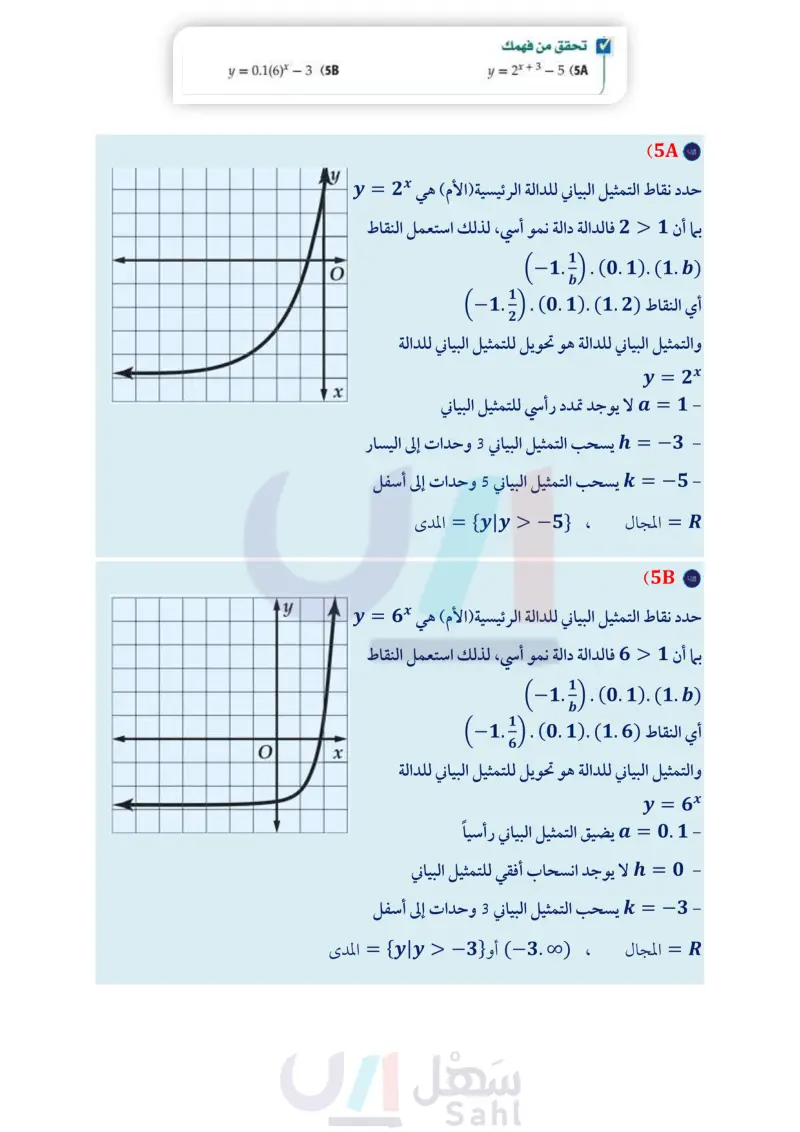
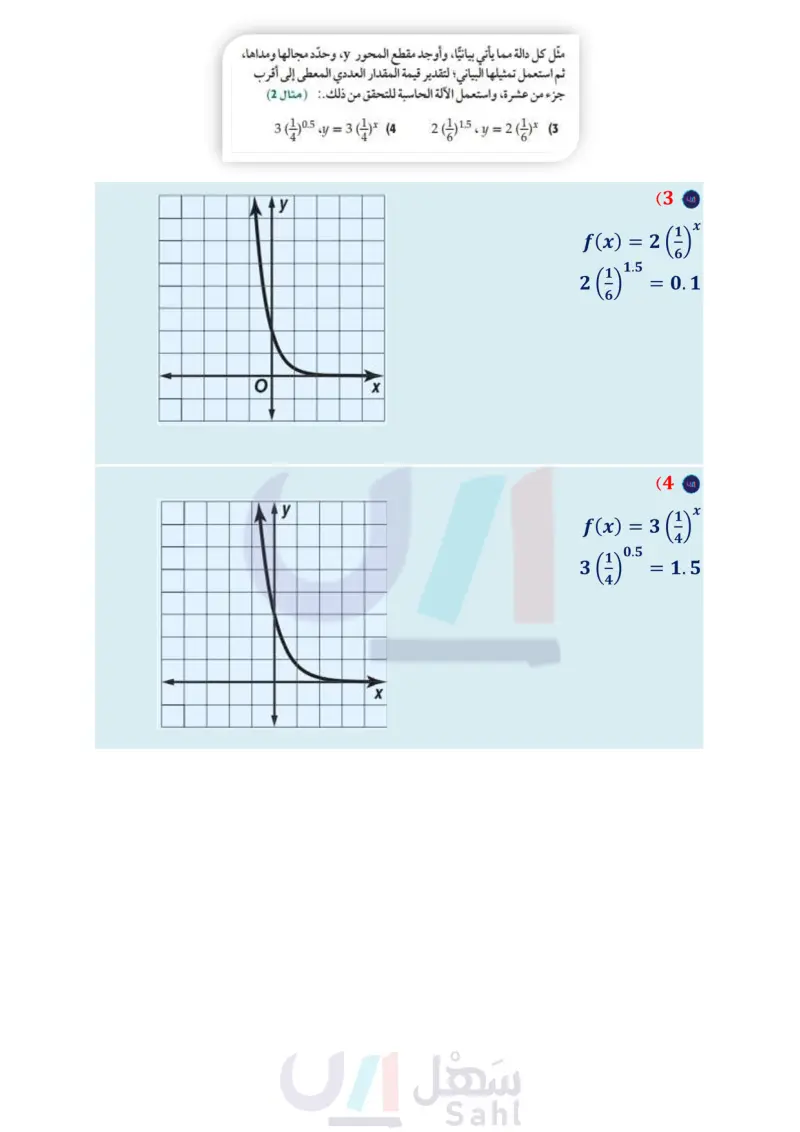
y = 2 6 У 5. 432H 1 5*-2 y = 5x إرشادات للدراسة تمثيل تحويلات الدالة الأسية بيانيا : يمكن استعمال إحدى الطريقتين الآتيتين؛ لتمثيل تحويلات دوال النمو الأسي والاضحلال الأسي بيانيا : استعمال التحويلات الهندسية للدالة الأم، وتعزيز ذلك بجدول لقيم الدالة عندما لا تكون التحويلات الهندسية كافية وواضحة؛ لمزيد من الدقة، كما في المثال y=-5x-2 (b حدد نقاط التمثيل البياني للدالة الأم 5 = y. بما أن 51 فالدالة (-1, دالة نمو أسي، لذا استعمل النقاط (1,0)، (01) ، ( 1 ) أي النقاط (15)، (0,1)، (1) والتمثيل البياني للدالة هو تحويل للتمثيل البياني للدالة y = 5x - 1 2 = a: ينعكس التمثيل البياني حول المحور x ويضيق رأسيًا. • 2 = يسحب التمثيل البياني وحدتين إلى اليمين. • 0 = :: لا يوجد انسحاب رأسي للتمثيل البياني. المجال هو مجموع تحقق من فهمك y = 2x + 3 – 5 (5 رعة الأعداد الحقيقية (R) ، والمدى هو {0 > y | y} 6 y = 0.1(6)x - 3 (5B 3 x 54 استعمال التحويلات الهندسية للدالة الأم فقط، كما في المثالين 5B,6 مثال 6 تمثيل تحويلات دوال الاضمحلال الأسي بيانيًّا مثل الدالة 3 - 2 (1) * +2 x 2 = y بيانيًّا، وحدد مجالها ومداها. حدد نقاط التمثيل البياني للدالة الأم " (1) = y . بما أن 1 > 4 > 0؛ فالدالة دالة اضمحلال أسي، لذا (−1,4). (0,1). (1,141) bläll Jarünl x والتمثيل البياني للدالة هو تحويل للتمثيل البياني للدالة (4) = y . • 2 = a : يتسع التمثيل البياني رأسيا. • 2- = : يسحب التمثيل البياني وحدتين إلى اليسار. • 3- = : يسحب التمثيل البياني 3 وحدات إلى أسفل. y * (4) * -1 012 X x | y = 2(1) *+2 −3 -3 المجال هو مجموعة الأعداد الحقيقية، والمدى هو مجموعة الأعداد الحقيقية الأكبر من 3 . تحقق من فهمك = 3/00 (3) X + 1 (6 تدرب وحل المسائل مثل كل دالة مما يأتي بيانيًا، وأوجد مقطع المحور y، وحدد مجالها ومداها، مثل كل دالة مما يأتي بيانيًا، وأوجد مقطع المحور y، وحدد مجالها ومداها، ثم استعمل تمثيلها البياني؛ لتقدير قيمة المقدار العددي المعطى إلى أقرب ثم استعمل تمثيلها البياني؛ لتقدير قيمة المقدار العددي المعطى إلى أقرب جزء من عشرة ، واستعمل الآلة الحاسبة للتحقق من ذلك. (مثال (1) جزء من عشرة، واستعمل الآلة الحاسبة للتحقق من ذلك. (مثال (2) 3 (4)0.5 y = 3 (4)* (4 2 (1) 1.5 y = 2 (¹) (3 5 حاسوب يزداد انتشار فيروس في شبكة حاسوبية بمعدل %25 كل دقيقة. إذا دخل الفيروس إلى جهاز واحد عند البداية، فأوجد دالة أسية تمثل النمو في انتشار الفيروس منذ البداية، ثم مثلها بيانيا باستعمال الحاسبة البيانية ( مثال (3) وزارة التعليم الدرس 1-2 الدوال الأسية of 85 2024-1446 21.5 ، y = 2* (1 2(8) −0.5. y = 2(8)* (2

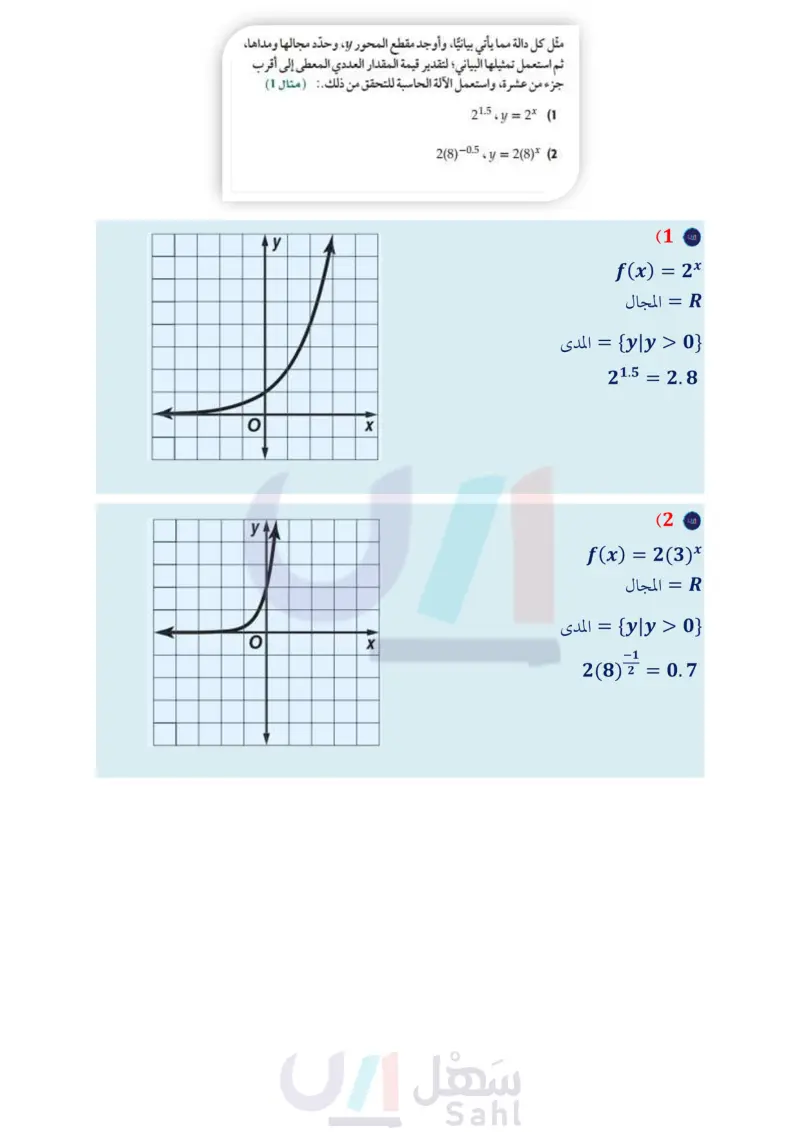
مثل كل دالة مما ياتي بيانيا، وأوجد مقطع المحور y ، وحدد مجالها ومداها، ثم استعمل تمثيلها البياني لتقدير قيمة المقدار العددي المعطى لأقرب جزء من عشرة.


مثل كل دالة مما ياتي بيانيا، وأوجد مقطع المحور y ، وحدد مجالها ومداها، ثم استعمل تمثيلها البياني لتقدير قيمة المقدار العددي المعطى لأقرب جزء من عشرة.

تمثيل تحويلات الدالة الاسية بيانيا
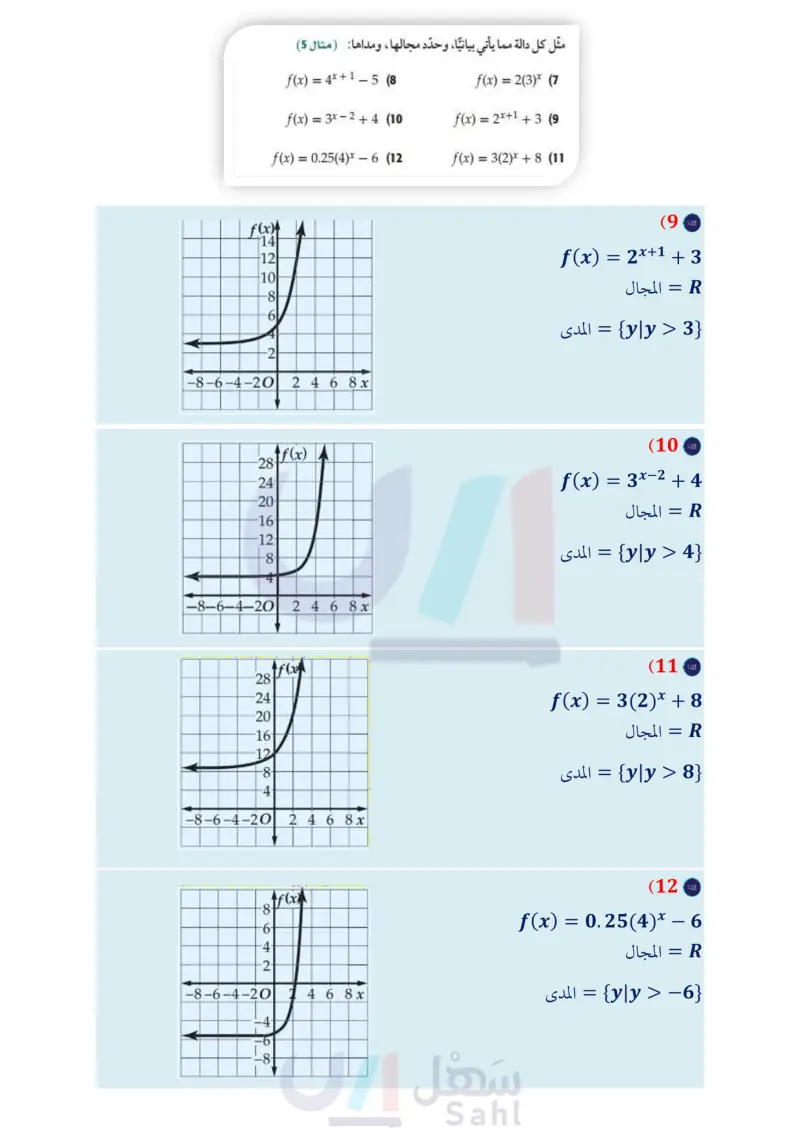
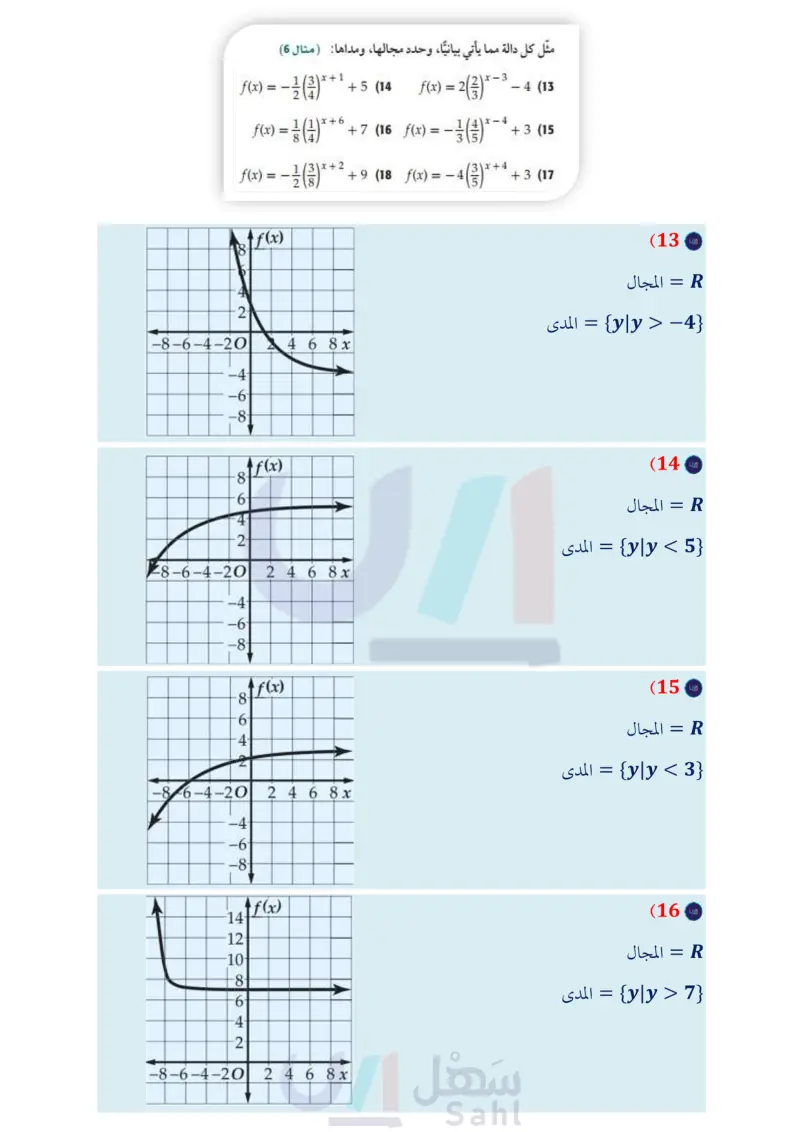
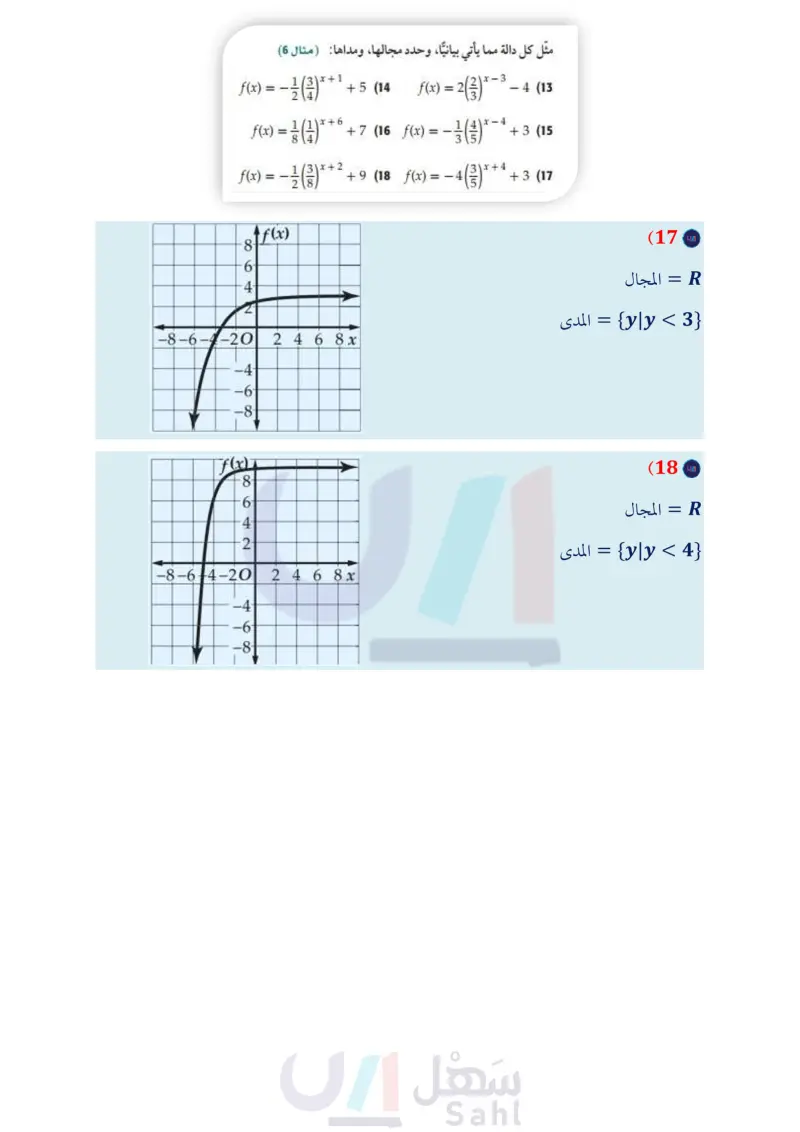
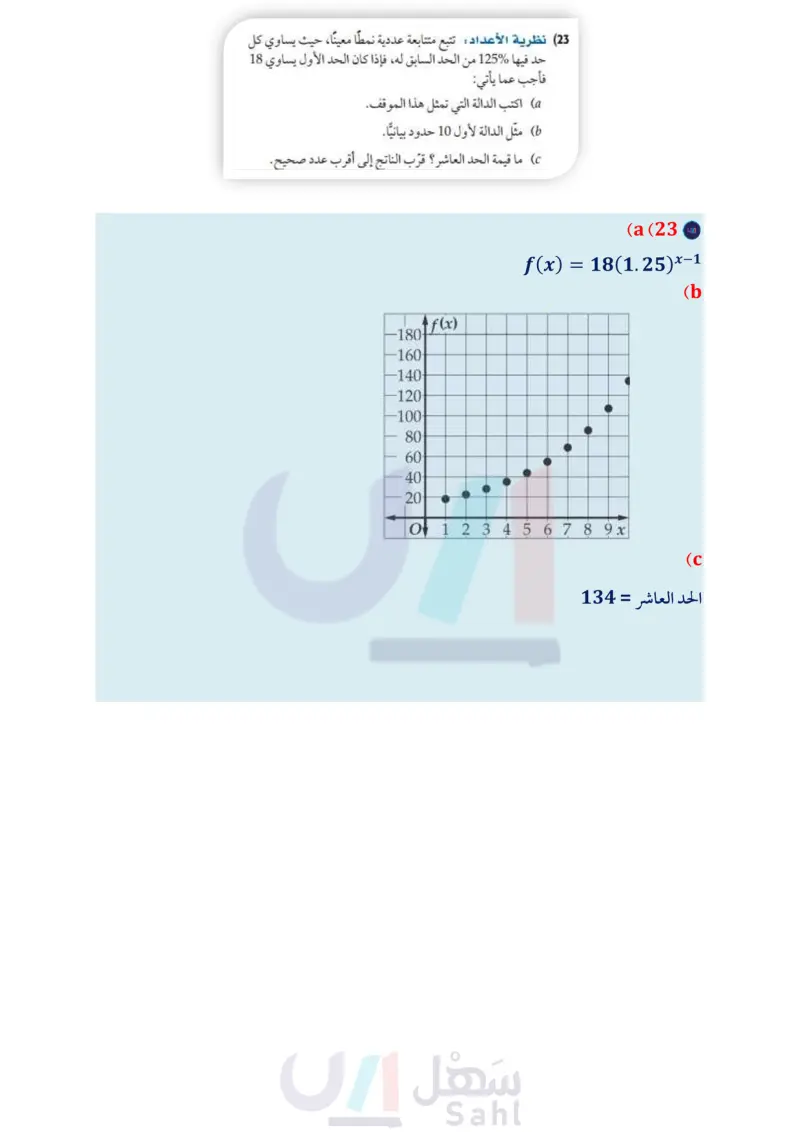
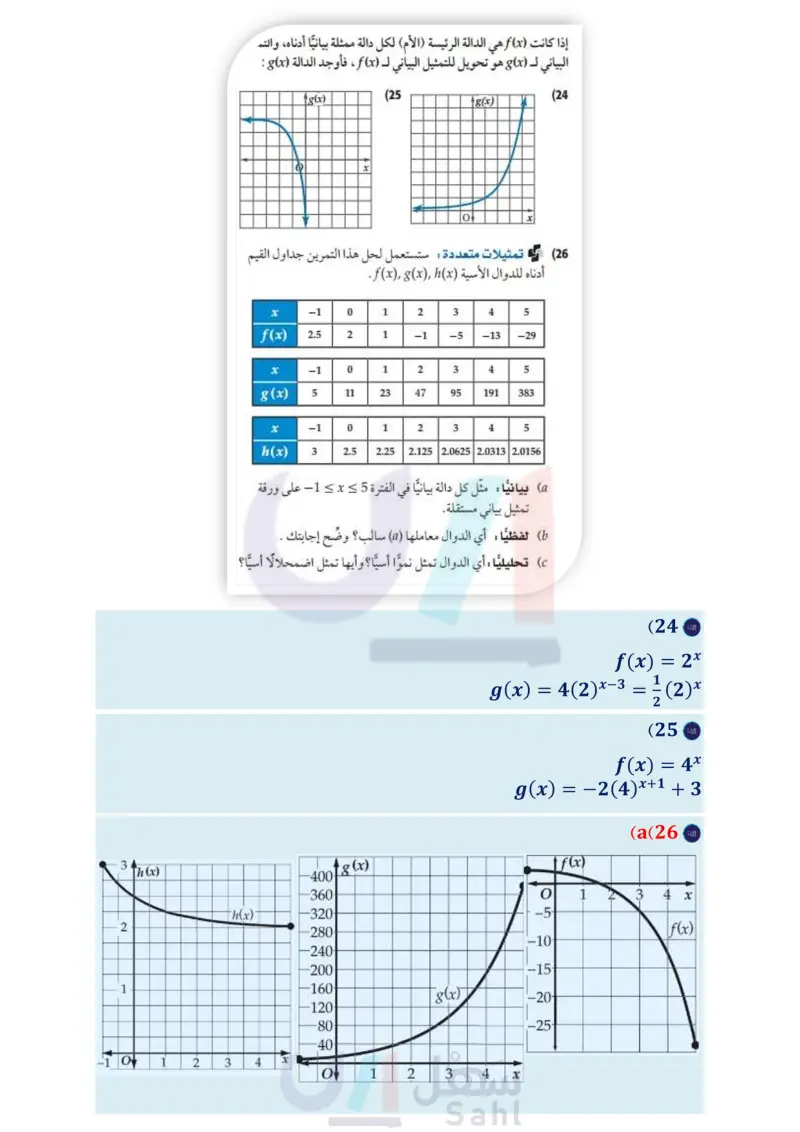
t %10 مما تبقى من المادة المحقونة. (6) سيارات سيارة كان سعرها 80000 ريال، ثم بدأ يتناقص بمعدل (22) صحة أخذ مريض حقنة، وفي كل يوم تلى ذلك، استهلك جسمه %15 كل سنة. أوجد دالة أسية تمثل سعر السيارة بعد ٤ سنة من شرائها، ثم مثلها بيانيًا باستعمال الحاسبة البيانية. ثم قدر سعر السيارة بعد 20 سنة من شرائها. (مثال (4) مثل كل دالة مما يأتي بيانيًا، وحدّد مجالها، ومداها (مثال (5) f(x) = 4x + 1 - 58 ( مثل الدالة التي تعبّر عن هذا الموقف بيانيا. ( متى يكون في جسم المريض أقل من 50% من المادة المحقونة؟ ( كم يبقى من المادة المحقونة في الجسم بعد 9 أيام؟ (23) نظرية الأعداد : تتبع متتابعة عددية نمطا معينًا، حيث يساوي كل حد فيها 125% من الحد السابق له فإذا كان الحد الأول يساوي 18 فأجب عما يأتي: f(x) = 2(3)x (7 f(x) = 3x - 2 + 4 (10 f(x) = 2x+1 + 3 (9 f(x) = 0.25(4)* – 6 (12 f(x) = 3(2)* + 8 (11 (24 (b اكتب الدالة التي تمثل هذا الموقف. ( مثل الدالة لأول 10 حدود بيانيا. ما قيمة الحد العاشر ؟ قرب الناتج إلى أقرب عدد . صحيح. إذا كانت (f(x هي الدالة الرئيسة (الأم) لكل دالة ممثلة بيانيًا أدناه، والتمثيل البياني لـ (x) هو تحويل للتمثيل البياني لـ (f(x ، فأوجد الدالة (x) : g(x) (25 6 (g(x) مثل كل دالة مما يأتي بيانيًا، وحدد مجالها، ومداها : ( مثال 6) f(x) = - 13x+1 24 +5 (14 f(x) = 2(3) * - 3 4 (13 |f(x) = ½-½ (1) * 1/1\x + 6 8 +7 (16 f(x) = −31/13 (313) *¯ - (½) -4 + 3 (15 f(x) = = - 13x+2 28 +9 (18 f(x) = −4 (3/3) 3x+4 +3 (17 x x (26 تمثيلات متعددة ستستعمل لحل هذا التمرين جداول القيم أدناه للدوال الأسية (f(x), (x),(x . (19) علوم يتكاثر نحل في خلية، فيزداد العدد بمعدل 30% كل أسبوع. إذا كان عدد النحل في البداية 65 نحلة، فأوجد دالة أسية تمثل عدد النحل بعد t أسبوع، ومثلها بيانيًا باستعمال الحاسبة البيانية، عدد النحل بعد 10 أسابيع. تم قدر 20 كرة قدم : تناقص عدد الحضور المباريات فريق كرة قدم بمعدل %5% لكل مباراة بعد خسارته في أحد المواسم. أوجد دالة أسية تمثل عدد الحضور (y) في المباراة ) ، إذا كان عددهم في المباراة الأولى x -1 0 1 2 3 4 5 f(x) 2.5 2 1 -1 -5 -13 -29 x -1 0 1 2 3 4 5 5 11 23 47 95 191 383 45 223 g(x) x -1 0 1 2 3 4 5 h(x) 3 2.25 2.5 2.125 2.0625 2.0313 2.0156 23500 ، ومثلها بيانيًا باستعمال الحاسبة البيانية، ثم قدر عدد الحضور (a بيانيا : مثل كل دالة بيانيًا في الفترة 5 = x = 1- على ورقة a) في المباراة 15 (21) هواتف تناقص عدد الهواتف العمومية في الآونة الأخيرة نتيجة انتشار الهواتف المحمولة. فإذا كان عدد الهواتف العمومية بالآلاف في إحدى المدن يعطى بالدالة (0.9)2.28 = (P(x في السنة x منذ عام 1420 هـ . 86 ( مثل الدالة بيانيًا باستعمال الحاسبة البيانية. وضح ماذا يمثل مقطع (x) وخط التقارب في هذه الحالة. الفصل 2 العلاقات والدوال الأسية واللوغاريتمية تمثيل بياني مستقلة. (b) لفظيًّا : أي الدوال معاملها (a) سالب ؟ وضّح إجابتك . تحليليًّا : أي الدوال تمثل نموا أسيا؟ وأيها تمثل اضمحلالا أسيا ؟ (27) مدارس : يزداد عدد خريجي إحدى المدارس بمعدل 1.055 كل عام منذ عام 1434هـ . إذا كان عدد الخريجين عام 1434هـ 110 طلاب، فإن الدالة (1.055) 110 = N تمثل عدد الخريجين في العام t بعد العام 1434هـ . ما عدد الخريجين المتوقع في عام 1445هـ ؟ وزارة التعليم Ministry of Education 2024-1446

أخذ مريض حقنة، وفي كل يوم تلى ذلك، استهلك جسمه %10 مما تبقى من المادة المحقونة مثل الدالة التي تعبر عن هذا الموقف بيانيا.

تتبع متتابعة عددية نمطا معينا، حيث يساوي كل حد فيها %125 من الحد السابق له، فإذا كان الحد الأول يساوي 18 فأجب عما يأتي اكتب الدالة التي تمثل هذا الموقف

اذا كانت f(x) هي الدالة الرئسية (الام) لكل دالة ممثلة بيانيا ادناه، والتمثيل البياني لـ g(x) هو تحويل التمثيل البياني لـ f(x) ،أوجد g(x).

أوجد دالة أسية تمثل عدد الحضور (y) في المباراة (t) ،إذا كان عددهم في المباراة الأولى 23500 ومثلها بيانيا باستعمال الحاسبة البيانية ثم قدر عدد الحضور في المبارة 15

مسائل مهارات التفكير العليا مراجعة تراكمية استعمل التمثيل البياني لكل من الدالتين أدناه لتقدير الفترات التي تكون (28) تحد اكتب دالة أسية يمر منحناها بكل من النقطتين (16) (3) : فيها الدالة متزايدة، أو متناقصة أو ثابتة مقربة إلى أقرب 0.5 وحدة، ثم عزز (29) تبرير حدد ما إذا كانت كل من الجمل الآتية صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. وضّح إجابتك. a التمثيل البياني للدالة الأسية التي على الصورة y = abx - h + k يقطع المحور y . (b التمثيل البياني للدالة الأسية التي على الصورة y = abx - h + k يقطع المحور x إجابتك عدديًّا (الدرس 4-1) (34 y (35 y -4- -8 -4 0 8x 4 4 8x -4- f ( x ) = x - 3 x + 4 -8- -8- |f(x) = 0.5(x + 4)(x + 1)(x − 2) استعمل منحنى الدالة (f(x لتمثيل كل من الدالتين إذا كان 6 عددًا صحيحًا، فإن الدالة || = (f(x هي دالة ( | x) = | f(x)\, h(x) = f ( x) بيانيا (الدرس 5-1) نمو أسي. (30) اكتشف الخطأ : طُلب إلى عمر وماجد أن يمثلا الدالة 1 - " ( 3 - = (f(x بيانيا. أي منهما تمثيله صحيح؟ وضّح 2/3) x- 34 إجابتك. f(x) = -4x + 2 (36) f(x) = Vx + 3 - 6 (37) أوجد () () (2) (۴۰) ((x), (f-g) (+) للدالتين (f(x), g(x كل مما يأتي، وحدد مجال كل من الدوال الناتجة (الدرس 6-1) f(x) = x x + 1 g(x) = x 2 - 1 - (39 f(x) = x² - 2x (38 g(x) = x+9 تدريب على اختبار ماجد عمر f(x) +f(x) -6- 8 6 -8- -2- 42 4 8642 2 -8-6-4-20 4 68x -8-6-4-20 2 4 6 8 x -4- -4- -6. -6- -8 -8 6 X 31) تحد: تتناقص مادة بنسبة 35% مما تبقى كل يوم، إذا بقي منها 8mg بعد 8 أيام، فكم ملجرامًا من المادة كان موجودًا في البداية؟ b x 32) مسألة مفتوحة: أعط قيمة للثابت b تجعل الدالة ) = (f(x دالة اضمحلال أشي. (40) أي من الأعداد الآتية لا ينتمي إلى مجال الدالة f(x) = V4 - 2x ؟ 3 A 2 B 1 C OD (41) إذا كانت f(x) = x + 1 ) ( x ) = 4x فما قيمة (2) (fog)؟ √3 A 4√√√3 B 3C 8D وزارة التعليم الدرس 1-2 الدوال الأسية of 87 2024-1446 (33) اكتب صف التحويل الذي ينقل الدالة x) = bx) إلى الدالة . f(x) = abx - h + k -