الدوال الرئيسية الأم والتحويلات الهندسية - رياضيات1-3 - ثالث ثانوي

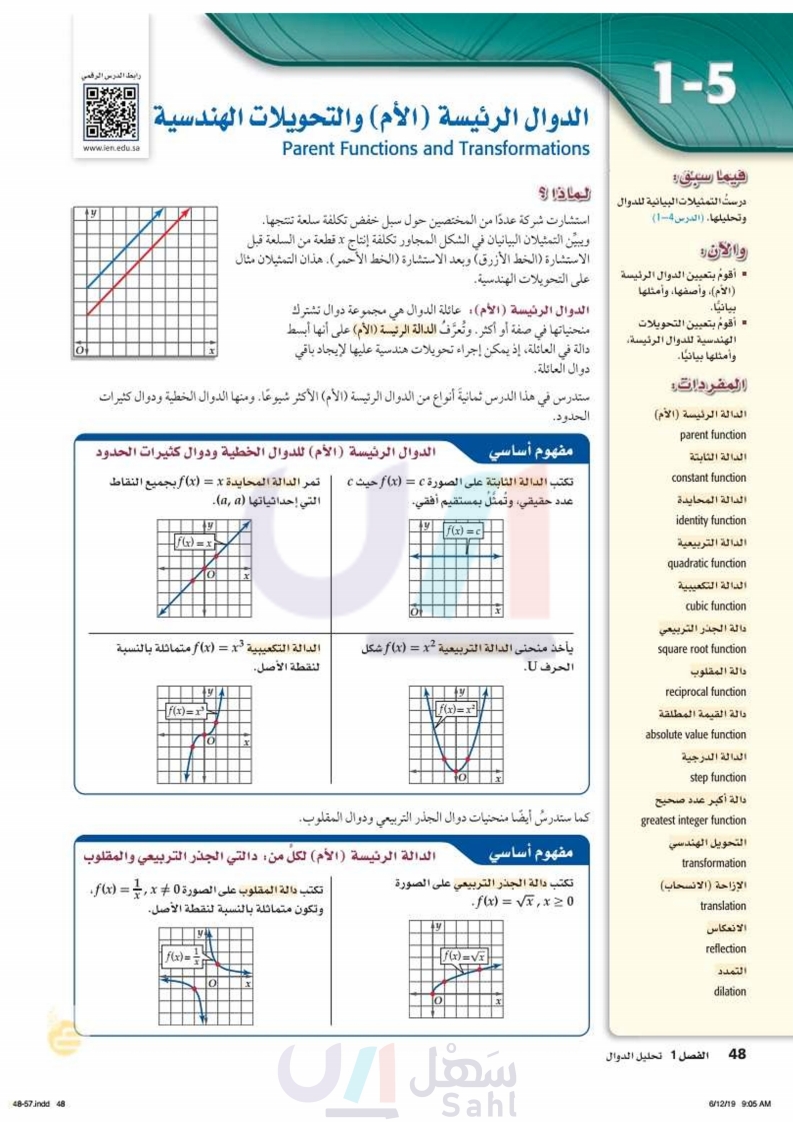
الدوال الرئيسة (الأم) والتحويلات الهندسية رابط الدرس الرقمي www.ien.edu.sa ΟΙ Parent Functions and Transformations 1-5 فيما سبق: درست التمثيلات البيانية للدوال وتحليلها. ( الدرس 4-1) والآن : أقوم بتعيين الدوال الرئيسة لماذا ؟ استشارت شركة عددًا من المختصين حول سبل خفض تكلفة سلعة تنتجها. ويبين التمثيلان البيانيان في الشكل المجاور تكلفة إنتاج x قطعة من السلعة قبل الاستشارة (الخط الأزرق) وبعد الاستشارة الخط الأحمر). هذان التمثيلان مثال على التحويلات الهندسية. (الأم)، وأصفها، وأمثلها الدوال الرئيسة (الأم) : عائلة الدوال هي مجموعة دوال تشترك منحنياتها في صفة أو أكثر. وتُعرَّفُ الدالة الرئيسة (الأم) على أنها أبسط بيانيا. أقوم بتعيين التحويلات الهندسية للدوال الرئيسة وأمثلها بيانيًا. المفردات: الدالة الرئيسة (الأم) parent function الدالة الثابتة constant function العائلة، إذ يمكن إجراء تحويلات هندسية عليها لإيجاد باقي دالة في دوال العائلة. x ستدرس في هذا الدرس ثمانية أنواع من الدوال الرئيسة (الأم) الأكثر شيوعًا. ومنها الدوال الخطية ودوال كثيرات الحدود. مفهوم أساسي الدوال الرئيسة (الأم) للدوال الخطية ودوال كثيرات الحدود تكتب الدالة الثابتة على الصورة f(x) = c حيث C تمر الدالة المحايدة f(x) = x بجميع النقاط عدد حقيقي، وتمثل بمستقيم أفقي. التي إحداثياتها (a, a) و y y |f(x) = x 10 x ot | f(x) = c x يأخذ منحنى الدالة التربيعية f(x) = x2 شكل الدالة التكعيبية x = (f(x متماثلة بالنسبة YA | f(x) = x3 | O 8 لنقطة الأصل. y |f(x) = x²| x الحرف U. كما ستدرسُ أيضًا منحنيات دوال الجذر التربيعي ودوال المقلوب. مفهوم أساسي الدالة الرئيسة (الأم) لكل من : دالتي الجذر التربيعي والمقلوب تكتب دالة المقلوب على الصورة 0 + f(x) = x ، ' 1 x وتكون متماثلة بالنسبة لنقطة الأصل. وزارة التعليم Ministry of Education 2024-1446 f(x) = 18 تكتب دالة الجذر التربيعي على الصورة • f (x) = √√x, x ≥ 0 +y f(x) =V O x الدالة المحايدة identity function الدالة التربيعية quadratic function الدالة التكعيبية cubic function دالة الجذر التربيعي square root function دالة المقلوب reciprocal function دالة القيمة المطلقة absolute value function الدالة الدرجية step function دالة أكبر عدد صحيح greatest integer function التحويل الهندسي transformation الإزاحة (الانسحاب) translation الانعكاس reflection الفصل 1 تحليل الدوال التمدد dilation 46

x كما تُعَدُّ دالة القيمة المطلقة إحدى الدوال الرئيسة (الأم). مفهوم أساسي دالة القيمة المطلقة الرئيسة (الأم) التعبير اللفظي: يُرمز لدالة القيمة المطلقة، بالرمز | f(x) = | x، ويأخذ منحناها شكل الحرف V ، وتعرف على النحو الآتي: النموذج y أمثلة : -x f(x) = x x < 0 x > 0 |-5| = 5, |0| = 0, |4| = 4 X f(x)=|x|| أما الدالة الدرجية، فهي دالة متعددة التعريف يُشبه تمثيلها البياني الدرج، ومن الأمثلة المشهورة على هذا النوع دالة أكبر عدد صحيح. مفهوم أساسي دالة أكبر عدد صحيح التعبير اللفظي: يرمز لدالة أكبر عدد صحيح بالرمز [f(x) = [x، وتعرف بأنها أكبر عدد صحيح أقل من أو يساوي x . أمثلة : [−4] = −4, [−1.5] = −2, = 0 [3] = النموذج | f(x)= [x] y x باستعمال ما تعلمته في الدروس السابقة، فإنه يمكنك وصف خصائص كل دالة من الدوال الرئيسة (الأم). ممّا يساعدك على تعرف منحنيات دوال أكثر تعقيدًا من العائلة نفسها وتحليلها. مثال 1 وصف خصائص الدالة الرئيسة (الأم) |f(x)=√x y الشكل 1.5.1 صف خصائص منحنى الدالة الرئيسة (الأم) f(x) = V في الشكل 1.5.1) : المجال والمدى والمقطع x والمقطع ل والتماثل والاتصال وسلوك طرفي التمثيل البياني وفترات التزايد والتناقص. خصائص منحنى دالة الجذر التربيعي (الشكل 1.5.1) هي: . مجال الدالة ,0]، ومداها ( ,0]. . للمنحنى مقطع واحد عند (0). المنحنى غير متماثل؛ لذا فإن الدالة ليست زوجية ولا فردية. • المنحنى متصل عند جميع قيم المجال. يبدأ المنحنى عند 0 = x وتكون lim f(x) = oo • المنحنى متزايد في الفترة (0) تحقق من فهمك XX X ارسم الدالة المعطاة وحدد المجال والمدى والمقطع والمقطع y والتماثل والاتصال وسلوك طرفي التمثيل البياني وفترات التزايد والتناقص. f(x) = |x| (1 التحويلات الهندسية تؤثر التحويلات الهندسية في شكل منحنى الدالة الرئيسة (الأم). فبعض التحويلات تغيّر موقع المنحنى فقط، ولا تغير أبعاده أو شكله، وتسمى تحويلات قياسية. وبعضها الآخر يغير شكل المنحنى وتسمى تحويلات غير قياسية وزارة التعليم الدرس 5-1 الدوال الرئيسة (الأم) والتحويلات الهندسية M47 of E 2024-1446

الانسحاب (الإزاحة) أحد التحويلات القياسية التي تنقل منحنى الدالة. فالانسحاب الرأسي ينقل منحنى الدالة f إلى أعلى أو إلى أسفل، بينما ينقل الانسحاب الأفقي منحنى الدالة إلى اليمين أو إلى اليسار. مفهوم أساسي الانسحاب الرأسي والانسحاب الأفقي الانسحاب الرأسي : الانسحاب الأفقي منحنى + (x) = f(x) هو منحنى (f(x مزاحا منحنى ) - x) = f(x) هو منحنى (f(x مزاحًا: . وحدة إلى أعلى عندما 0 < . || من الوحدات إلى أسفل عندما 0 > k . . |g (x) = f(x) + k |y = f(x)= . من الوحدات إلى اليمين عندما 0 . || من الوحدات إلى اليسار عندما 0 > h . الله | y = f(x) | X |g(x) = f(x_h) \WA |g(x) = f(x + h)| O | y = f(x) | X |y = f(x) x x g(x)=f(x)-k مثال 2 انسحاب منحنى الدالة استعمل منحنى الدالة الرئيسة (الأم) || = (f(x لتمثيل كل دالة من الدوال الآتية بيانيا : g(x) = |x| +4 (a هذه الدالة على الصورة ) + (f(x = ) ، وعليه فإن منحنى (x) هو منحنى |f(x) = x مزاحًا 4 وحدات إلى أعلى كما في الشكل 1.5.2. وزارة التعليم Ministry of Education 2024-1446 g(x)=x+3| (b هذه الدالة على الصورة 3 (x) = f(x) أو (3) - x) = fx)، وعليه فإن منحنى (x) هو منحنى || = (f(x مزاحًا 3 وحدات إلى اليسار كما في الشكل 1.5.3. g(x) = |x − 2 —– 1 (c - - هذه الدالة على الصورة 1 - 2 - (x) = f(x)، أي أن منحنى (x) هو منحنى الدالة |f(x) = |x مزاحًا وحدتين إلى اليمين ووحدة واحدة إلى أسفل كما في الشكل 1.5.4. y |f(x)=|x|| |f(x)= |x| X |f(x)=|x|| - 8 (x) = x - 2 - 1 |g(x) = | x + 3 | X الشكل 1.5.4 الشكل 1.5.3 إرشاد تقني الانسحاب : يمكنك إجراء انسحاب لمنحنى دالة باستعمال الحاسبة البيانية TI-nspire ، بعد تمثيل الدالة الرئيسة (الأم) : f1(x) • لإجراء انسحاب مقداره k وحدة لأعلى أو لأسفل اضغط على المفاتيح: | g(x) = | x | + 4 tab var f1(x)+k enter الشكل 1.5.2 X تحقق من فهمك استعمل منحنى الدالة الرئيسة (الأم) 3 f(x) = x لتمثيل كل دالة من الدوال الآتية بيانيا : h(x) = (x+2)³ +4 (2C h(x) = 8 + x3 (2B h(x)=x35 (2A . لإجراء انسحاب مقداره h وحدة لليمين أو اليسار اضغط على tab var f1(x+h) المفاتيح : enter ستقوم الحاسبة كلا برسم الدالتين الرئيسة (الأم) والدالة المزاحة على الشاشة نفسها. الفصل 1 تحليل الدوال 48

من التحويلات القياسية الأخرى الانعكاس، والذي يُكوّن لمنحنى الدالة صورة مرآة بالنسبة لمستقيم محدّد. مفهوم أساسي الانعكاس حول المحورين الإحداثيين الانعكاس حول المحور لا الانعكاس حول المحور x منحنى الدالة (x) = - f(x) هو انعكاس لمنحنى منحنى الدالة (g(x) = f(x هو انعكاس لمنحنى الدالة (f(x حول المحور y . الدالة (f(x حول المحور x . |g(x) = f(x) | y = f(x) x y = f(x) x |g(x) = − f(x)| كن ن دقيقًا عند كتابة المعادلة الناتجة عن التحويل الهندسي لدالة، فمثلًا منحنى الدالة 2 + 1 - g(x) = - Vx يختلف عن منحنى الدالة 2 + 1 - x) = - (Vx) 12 O y |g(x) = −√√x − 1 + 2 - X y O x |g(x) = − (√√ x − 1 +2) انسحاب لمنحنى الدالة ) = (f(x وحدة إلى اليمين ووحدتين إلى أعلى، ثم انعكاس حول المحور x . انسحاب وحدة إلى اليمين ثم انعكاس لمنحنى الدالة f(x) = VT حول المحور x ، ثم انسحاب وحدتين إلى أعلى. كتابة معادلات التحويل مثال 3 صف العلاقة بين منحنى الدالة f(x) = x2 في الشكل (1.5.5 ومنحنى (g (x في كل مما يأتي، y (b y = g(x) | x 0 y ثم اكتب معادلة (x) : y= g(x) x 8 منحنى الدالة و هو انسحاب لمنحنى f(x) = x2 منحنى الدالة 8 هو انعكاس لمنحنى f(x) = x2 بمقدار 5 وحدات إلى اليمين ثم انعكاس حول حول المحور x ثم انسحاب وحدتين إلى أعلى، أي x²+201 أن · g(x) = ·⋅ المحور x ، أي أن 52 - - = (x) تحقق من فهمك صف العلاقة بين منحنيي } = (f(x و (x) ثم اكتب معادلة ( g ( x في كل من السؤالين الآتيين : y (3B y = g(x) X وزارة التعليم الدرس 5-1 الدوال الرئيسة (الأم) والتحويلات الهندسية M49 of E 2024-1446 X | y= g(x) (3A Ay |f(x) = x² x الشكل 1.5.5

التمدد هو تحويل غير قياسي يؤدي إلى تضيق (ضغط) أو توسع (مط) منحنى الدالة رأسيًا أو أفقيًا. مفهوم أساسي التمدد الرأسي والتمدد الأفقي التمدد الأفقي التمدد الرأسي إذا كان a عددًا حقيقيًا موجبًا، فإن منحنى الدالة إذا كان a عددًا حقيقيًا موجبًا، فإن منحنى الدالة : 9s g(x) = a f(x) • توسع رأسي لمنحنى (f(x ، إذا كانت 1 < a . 6 . تضيق رأسي لمنحنى (f(x ، إذا كانت 1 > a > 0 (g(x) = f (ax هو: تضيق أفقي لمنحنى (f(x، إذا كانت 1 < a . • توسع أفقي لمنحنى (f(x ، إذا كانت 1 > a> 0 |g(x)=f(ax), a >1 y |y = f(x)| x y = f(x) | x |g(x) = f(ax), 0 < a <1 |g(x) = a•f(x), a >1 |y = f(x)| x ky = f(x) |g(x) = a•f(x), 0<a<1 x مثال 4 وصف التحويلات الهندسية وتمثيلها عين الدالة الرئيسة (الأم) (f(x للدالة ( g ( x في كل مما يأتي، ثم صف العلاقة بين المنحنيين، ومثلهما بيانيا في | f(x) = x3 4 Ο y x -18(x) = 1x3 4 4 2 f(x) = x²| 20 2 4x |g(x)=-(2x)² المستوى الإحداثي. g(x) = 1 x³ (a منحنى الدالة (x) هو تضيق رأسي لمنحنى f(x) = x3 ؛ لأن .0 > 4 13 0<<1; g(x) = x³ = f(x) 1 g(x)=(2x)2 (b منحنى الدالة (x) هو تضييق أفقي لمنحنى f(x) = x2 أولًا؛ لأن 2( f(x) = x2, f(2x) = (2x وَ 2 > 1، ثم انعكاس حول المحور ؛ لأن (2x2 = - f(2x) تحقق من فهمك = 8(x): 8(x) = 5 +3 (4B g(x) = [x] (4A يمكنك تمثيل الدالة المتعددة التعريف بيانيًّا باستعمال التحويلات الهندسية التي درستها . وزارة التعليم Ministry of Education 2024-1446 إرشادات للدراسة التمدد: يظهر التمددان متشابهين أحيانًا مثل التوسع الرأسي والتضيق الأفقي؛ لذا يصعب وصف التمدد الذي طبق على المنحنى، وفي هذه الحالة عليك المقارنة بين معادلة الدالة الناتجة عن التحويل والدالة الرئيسة (الأم). الفصل 1 تحليل الدوال 50

مثال 5 تمثيل الدوال متعددة التعريف بيانيا x < -1 3x2 . f(x) = { -1 مثل الدالة بيانيا: 4 x 1 x ≥4 (x-5)³ +2 الفترة ( 1 ) ، أمثل الدالة y = 3x2 . في ' في الفترة - أمثل الدالة الثابتة -1- = في الفترة (4] أمثل الدالة 2 + 53 - y = (x . ضع دائرة مفتوحة عند كل من النقطتين (1) و (41) ونقطة عند كل من f(4)=1,f(−1)=−1;Y(4,1),(−1,−1) تحقق من فهمك Ay 10 X (x+6)² x<-5 - x - 5 x ≤0 ' h(x)=7 -5≤x≤2 (5B g(x) = x3 0 < x = 2 (5 |4x| x2 اله 2 x> 2 X SAFF الاتحاد السعودي لكرة القدم SAUDI ARABIAN FOOTBALL FEDERATION الربط مع الحياة يمكنك استعمال التحويلات الهندسية التي تعلمتها على الدوال التي تمثل مواقف من واقع الحياة. مثال 6 من واقع الحياة التحويلات الهندسية على الدوال - 1 15 كرة قدم ركل لاعب كرة قدم فكان مسارها معطى بالدالة 1 + x2 + 4x = - = ) ، حيث يمثل ارتفاع الكرة بالياردة عن سطح الأرض، وتمثل x المسافة الأفقية بالياردة التي تقطعها الكرة حيث 0 = x ترتبط بخط منتصف الملعب. صف التحويلات التي تمت على الدالة الرئيسة (الأم) 2 f(x) = x للحصول على (x) . تأسس الاتحاد العربي السعودي لكرة أعد كتابة الدالة لتصبح على الصورة 2 - h(x) = ax باستعمال إكمال القدم عام 1956م، وقد انضم إلى الفيفا نفسه. والاتحاد الآسيوي في العام نفـ المربع. مسار الكرة 1 80 y h(x) = - + x + 4x + 1 15 == x 40 20 60 80 المسافة الأفقية (بالياردة) 60 40 20 = - 15 1 x 2 + 4x + 1 = - · 60x) + 1 (x2 15 (x-2 - 60x + 900) + 1 + 1/3 (900) 15 1 15 (x - 30)² +61 15 (h(x الدالة الأصلية حلل x2 + 4x - 1 15 أكمل المربع المسافة الرأسية (بالياردة) اكتب 900 + x 2 - 60x على صورة مربع كامل ثم بسط أي أن منحنى (x) ينتج من منحنى ( f ( x من خلال التحويلات الآتية على الترتيب انسحاب 30 وحدة إلى اليمين، وتضييق رأسي بمقدار 1 ، ثم انعكاس حول المحور x ، وانسحاب 61 وحدة إلى أعلى. 15 تحقق من فهمك كهرباء إذا كانت شدة التيار (x) بالأمبير الذي يمر بجهاز DVD تعطى بالدالة V حيث x القدرة بالواط والعدد 11 هو المقاومة بالأوم. صف التحويلات التي تمت على الدالة f(x) = V للحصول على الدالة (x) . اكتب دالة تصف مرور تيار في مصباح مقاومته 15 أوم. I(x) = وزارة التعليم الدرس 5-1- الدوال الرئيسة (الأم) والتحويلات الهندسية M51y of E 2024-1446

إرشاد تقني تحويلات القيمة المطلقة يمكنك التحقق من أثر التحويل الهندسي على منحنى القيمة المطلقة باستعمال الحاسبة البيانية. ويمكنك أيضًا تمثيل كلا الدالتين في المستوى الإحداثي نفسه تُستعمل تحويلات هندسية أخرى غير قياسية تتضمن القيمة المطلقة مفهوم أساسي التحويلات الهندسية مع دوال القيمة المطلقة g(x) = |f(x)| g(x) = f(|x|) يُغير هذا التحويل الهندسي أي جزء من منحنى يغير هذا التحويل الهندسي جزء منحنى الدالة الدالة يقع تحت المحور x ليصبح فوقه بالانعكاس الموجود إلى يسار المحور ل ويضع مكانه صورة جزء المنحنى الواقع إلى يمين المحور ل حول المحور x. y بالانعكاس حول المحور لا . |y = f(x), Xx W V W O y = f(x) x x x |g(x) = f(|x|)| |g(x) =|f(x)|| x y | f(x) = x3 - 4x | الشكل 1.5.6 مثال 7 وصف التحويلات الهندسية وتمثيلها استعمل منحنى الدالة f(x) = x3 - 4x المبين في الشكل 1.5.6 لتمثيل كل من الدالتين الآتيتين بيانيا : g(x) = |f(x)| (a h(x) = f(|x|) (b يقع الجزء السالب من منحنى (f(x في الفترتين ضع مكان جزء المنحنى الموجود إلى يسار المحور y (2) و (2)؛ لذا يتم عكس هذين الجزأين انعکاس الجزء الموجود إلى يمينه حول المحور y. حول المحور x ويترك الجزء الباقي من المنحنى دون تغيير. وزارة التعليم Ministry of Education 2024-1446 ⭑y x |h(x) = f(x1) My W 0 x |g(x)=|f(x)|| تحقق من فهمك استعمل منحنى الدالة (f(x في كلِّ من الشكلين أدناه؛ لتمثيل كلّ من الدالتين | (x) = f(x) و |x) = f(x) بيانيا : (7B y f(x) = [2x] y x 0 x f(x) = 5 3x - 4 (7A الفصل 1 تحليل الدوال 52

x<-2 -2≤x≤7 (21 تدرب وحل المسائل صف خصائص كل دالة من الدوال الرئيسة (الأم) الآتية: المجال، والمدى والمقطع ، والمقطع ، والتماثل، والاتصال، وسلوك طرفي التمثيل البياني، وفترات التزايد والتناقص (مثال (1) مثل منحنى كل من الدوال الآتية بيانيا : ( مثال (5) f(x) = = -2 3 (x-5)²+2, x≥7 f(x) = x3 (3 f(x) = 1½ (2 x f(x) = [x] (1 x +4 x<-6 ' 8(x) = 1 x 6 |x − 5| -6≤x≤4 (22 f(x) = x (6 f(x) = c (5 f(x) = x2 (4 ' x > 4 =1 استعمل منحنى الدالة الرئيسة (الأم) f(x) = V لتمثيل كل من الدالتين x < -3 الآتيتين: (مثال (2) h(x) = 4x - 3 √x -1 < x <3 x > 4 (23 g(x) = Vx - 4 (7 2 x<-4 g(x) = √√x −7+3 (8 g(x) = x43x3 +5, -1≤x<1 (24 [x] + 1 x≥3 x استعمل الدالة الرئيسة (الأم) - = (f(x لتمثيل كل من الدالتين الآتيتين: ( مثال (2) 8(x) = 1 ½ + 4 (9 g(x) = 4 (10 1 X x + 7 - (25) أسعار يبين الجدول أدناه سعر سلعة منذ عام 1411هـ حتى 1431هـ . استعمل هذه البيانات لتمثيل دالة درجية (مثال 5) . 1431 1427 1426 1424 1420 1416 1413 1411 العام صف العلاقة بين منحنيي [f(x) = [x و (x) في كل من الحالتين الآتيتين، ثم اكتب معادلة الدالة (x) (مثال (3) (11 y (12 8(x) g(x) x O x صف العلاقة بين منحنيي || = (f(x و (g(x في كل من الحالتين الآتيتين، ثم اكتب معادلة الدالة (x) : ( مثال (3) y (13 8(x) 4 y (14 -8 4g(x) -8-4 O -4- 4 8x -4 O 12x 8 4 -4- -8- اكتب الدالة الرئيسة (الأم) (f(x للدالة (g(x في كل مما يأتي، وصف العلاقة بين المنحنيين، ومثلهما في مستوى إحداثي واحد. (مثال 4) g(x) = 3|x| −4 (15 (17 4 g(x) = x + 1 8(x) = 1 +7 (19 6x g(x) = 3√√√x+8 (16 g(x) = 2[x6] (18 8(x) = = Vx + 3 4 (20 السعر (بالريال) 55 32 33 40 30 17 22 15 (26) أعمال : قدمت إحدى شركات الهواتف المحمولة عرضًا لمشتركي شبكتها بحيث يدفع المشترك مبلغًا ثابتًا شهريًا مقداره 20 ريالًا، ويدفع 0.2 ريال مقابل كل دقيقة اتصال. إن تكلفة هذا العرض على المشترك تعطى بالدالة [x) = 20 + 0.2 [x)، حيث x عدد دقائق الاتصال (مثال (6) (b صف التحويلات الهندسية التي تطبق على الدالة الرئيسة (الأم) [f(x) = [x لتمثيل الدالة (x). إذا قدمت الشركة عرضًا آخر بحيث يدفع المشترك فيه 30 ريالا شهريًا، ويدفع 0.1 ريال عن كل دقيقة اتصال. فاكتب الدالة التي تصف تكلفة هذا العرض. هل يمكن أن تتساوى التكلفة في العرضين؟ وكم يكون عدد دقائق الاتصال في هذه الحالة؟ (27) فيزياء : إذا علمت أن الطاقة المختزنة في نابض ما، تعطى بالدالة x) = 4x2) حيث تقاس الطاقة E بالجول، وتقاس المسافة بالمتر . ( مثال 6) صف التحويل الهندسي الذي تم على الدالة الرئيسة (الأم) f(x) = x2 للحصول على الدالة (x). إذا كانت الطاقة المختزنة في نابض ما، آخر تعطى بالدالة x) = 2x2) ، فمثل بيانيًّا كلا من الدالتين على الشاشة نفسها باستعمال الحاسبة البيانية. 6 وزارة التعليم الدرس 5-1 الدوال الرئيسة (الأم) والتحويلات الهندسية of E 53 2024-1446

وزارة التعليم Ministry of Education 2024-1446 استعمل منحنى الدالة (f(x في كل مما يأتي لتمثيل الدالتين (|x) = |f(x)\, h(x) = f (|x) بيانيا (مثال (7) (40) اكتب دالة تمثل المنحنى المرسوم: 12 y 8 00 4 -84024x f(x) = ½ (28 f(x) = x4 - x3 - 4x2 (29) = 1 f(x) - 3 x +5 (30 f(x) = Vx + 2 - 6 (31 اكتب الدالة الناتجة عن إجراء التحويلات الهندسية المعطاة على الدالة الرئيسة (الأم) في كل من السؤالين الآتيين: x 32) = (f(x : انسحاب 5 وحدات إلى أعلى، و7 وحدات إلى اليسار، وتوسع رأسي معامله 2 33) [f(x) = [x : انعكاس في المحور x و انسحاب 4 وحدات إلى أسفل، وتوسع رأسي معامله 3 فيزياء : إذا كانت المسافة التي يقطعها جسم تعطى بالدالة o t t + fat2 = ) ، حيث المسافة الابتدائية، و 70 السرعة الابتدائية و a تسارع الجسم. صف التحويلات الهندسية التي تمت على الدالة الرئيسة (الأم) (2) = (f(t) للحصول على (t) في كل مما يأتي: استعمل منحنى (f(x لتمثيل منحنى (g (x لكل مما يأتي: 8x My |f(x) g(x) = 0.25f(x) +4 (41 g(x) = 3f(x) - 6 (42 g(x) = f(x − 5) + 3 (43 - g(x) = −2f(x) +1 (44 4 10 -8- -8 (f(x لتمثيل كل دالة مما يأتي: g(x) = −3f(x) +6 (46 g(x) = f(2x + 1) +8 (48 = 8 √√x+6 استعمل 4 g(x) = 2f(x) +5 (45 g(x) = f(4x) — 5 (47 xo = 0, og = 2, a = 2 (34 xo = 10, g = 0, a = 2 (35) xo = 1, 00 = 8, a = 4 (36 xo = 3, 00 = 5, a = 3 (37 38 اكتب معادلة الدالة ( x ) ( إذا علمت أن منحناها ناتج عن عدة تحويلات هندسية لمنحنى الدالة (f(x ، وأحد هذه التحويلات هو تضييق رأسي معامله 0.5. -16 9 -8- -8 104 -4 8x (5,-8) f(x)=8 16 | 8(x), (49) تمثيلات متعددة سوف تستقصي في هذه المسألة بعض : العمليات على الدوال معتمدًا على الدوال الآتية: f(x) = x2 + x +7 • g(x)=4x+3• h(x) = x2 + 6x + 10 a) جدوليًّا : اختر ثلاث قيم لـ ه ، وأكمل الجدول الآتي: a f(a) g(a) f(a) + g(a) h(a) (39) تسوق: توقعت إدارة أحد المجمعات التجارية الجديدة أن يعطى عدد المتسوقين بالآلاف بالدالة f(x) = V7x خلال أول ستين يوما من الافتتاح، حيث x رقم اليوم بعد الافتتاح، 1 = x يرتبط بيوم الافتتاح اكتب دالة ( x ) بدلالة ( f ( x لكل حالة من الحالات الآتية: a زاد عدد الحضور 12% على المتوقع. تأخر موعد الافتتاح 30 يومًا بسبب تأخر أعمال البناء. نقص عدد المتسوقين 450 عن المتوقع. b) لفظيًّا : ما العلاقة بين (x) (x) f(x) جبريًا : أثبت صحة العلاقة التي حصلت عليها في الفرع b (c جبريًا. الفصل 1 تحليل الدوال 54

مسائل مهارات التفكير العليا 50 اكتشف الخطأ وَصَف كل من محمد وعبد الملك التحويلات الهندسية التي تمت للوصول إلى الدالة [4 + g(x) = [x. فقال محمد أنه تم سحب منحنى الدالة الرئيسة (الأم) 4 وحدات إلى اليسار. وقال عبد الملك: إنه تم سحب الدالة 4 وحدات إلى أعلى. فمن منهما كانت إجابته صحيحة ؟ برر إجابتك. 51) تبرير: إذا كانت (x) دالة فردية وكانت (x) انعكاسًا للدالة (f(x حول المحور x و (x) انعكاسا للدالة (x) حول المحور y ، فما العلاقة بين (f(x),(x برر إجابتك. 6 تبرير تحقق ما إذا كانت كل من الجملتين صحيحة أحيانًا أو صحيحة دائمًا أو ليست صحيحة. وبرّر إجابتك. (52) إذا كانت ( f ( x دالة زوجية فإن |(f(x) = |f(x (53) إذا كانت (x) دالة زوجية فإن (f(x) = - | f(x (54) تحد صف التحويلات الهندسية التي تمت على الدالة V = (f(x للوصول إلى دالة يمر منحناها بالنقطة (26). 1 (55) تبرير: وضّح الفرق بين التوسع الرأسي بمعامل مقداره 4، والتوسع الأفقي بمعامل مقداره 4 . ما النتيجة النهائية بعد إجراء كل من التحويلين الهندسيين على الدالة نفسها؟ (56) اكتب وضح أهمية الترتيب في تحويلات الانعكاس والانسحاب. مراجعة تراكمية أوجد متوسط معدل التغير لكلِّ من الدوال الآتية في الفترة المعطاة: ( الدرس 4-1) استعمل التمثيل البياني لكل دالة مما يأتي لتقدير قيمة كل من: المقطع ، والأصفار، ثم تحقق من إجابتك جبريًا، وقرب الناتج إلى أقرب جزء من مئة (الدرس 2-1 ) (63 (64 (65 4 -8-4 O 4 -4 8x y = (x - 42 - 3 + y = x3 - x2 - 2x -4 4- £8- 8x 100 | y = Vx - 2 - 1 Too 8x -8-4 O 4 -4- -8- تدريب على اختبار (66) ما الفترة التي تتزايد فيها الدالة الممثلة في الشكل أدناه؟ y y = f(x)| x g(x) = -2x² + x — 3, [−1, 3] (57 - g(x) = x2 – 6x + 1, [4, 8] (58 f(x) = -2x3 - x2 + x - 4, [2,3] (59) حدد سلوك طرف التمثيل البياني لكلِّ من الدوال الآتية عندما تقترب x من ما لانهاية، مستعملا التبرير المنطقي، وبرّر إجابتك (الدرس 3-1) (0,∞) A (-∞,1) B (-1,∞) C (1,00) D (62 9(x) = 12 (60 x 0.5 f(x) p(x) = = x+2 23 - 3 x- (61 x2 (67) ما مدى الدالة 8 + y = x ؟ 2 {y | y + +2V2} A {y | y ≥ 4} B {y|y≥ 0} C {y|y≤ 0} D وزارة التعليم الدرس 5-1- الدوال الرئيسة (الأم) والتحويلات الهندسية M55 of E 2024-1446