الاتصال والنهايات - رياضيات1-3 - ثالث ثانوي

رابط الدرس الرقمي www.ien.edu.sa الاتصال والنهايات Continuity and Limits 1-3 فيما سبق: درستُ إيجاد مجال الدالة ومداها باستعمال تمثيلها البياني (الدرس (12) والآن : أستعمل النهايات للتحقق من اتصال دالة، وأطبقُ نظرية القيمة المتوسطة على الدوال المتصلة. لماذا ؟ بمناسبة الافتتاح، قدم مركز للتموينات بطاقات خصم للمتسوقين وفقًا لقيمة مشترياتهم كما هو مبين في التمثيل البياني المجاور. يتضح من التمثيل البياني أن هناك نقاط انقطاع (قفزات) عند بعض القيم كما هو الحال عند x=600,x=900 الخصم في مركز التموينات 300 600 900 1200 1500 1800 قيمة المشتريات (بالريال) الاتصال : تكون الدالة متصلة إذا لم يكن في تمثيلها البياني أي انقطاع أو قفزة. وعليه أستعمل النهايات لوصف سلوك طرفي التمثيل البياني لدالة. المفردات: الدالة المتصلة continuous function النهاية limit الدالة غير المتصلة discontinuous function عدم الاتصال اللانهائي infinite discontinuity عدم ا م الاتصال القفزي يمكنك تتبع مسار المنحنى دون أن ترفع القلم عنه. إن أحد شروط اتصال دالة مثل (f(x عند x = C هو أن تقترب قيم الدالة من قيمة واحدة عندما تقترب قيم x من C من جهتي اليمين واليسار. إن مفهوم اقتراب قيم الدالة من قيمة دون الحاجة إلى الوصول إلى تلك القيمة يُسمى النهاية. مفهوم أساسي النهايات التعبير اللفظي : إذا كانت قيمة الدالة (f(x تقترب من قيمة واحدة L عندما تقترب x من c من الجهتين، فإن نهاية ( f ( x عندما تقترب x من c هي L . الرموز: نقول : إن lim f(x) = L ، وتُقرأ نهاية x-c الدالة (f(x عندما تقترب x من c هي L . lim f(x) = L |y = f(x) X1 X2 C X3 X4 x x 200 160 120 الخصم (بالريال) A | y = f(x) (f(x متصلة لجميع قيم . f(x2) L f(x3) f(x4) jump discontinuity عدم الاتصال القابل للإزالة إن التمثيل البياني للدالة غير المتصلة يساعدك على فهم المعنى الجبري للاتصال. وفيما يأتي ملخص لأهم حالات removable discontinuity عدم الاتصال غير القابل للإزالة nonremovable discontinuity سلوك طرفي التمثيل البياني end behavior عدم اتصال الدالة: مفهوم أساسي أنواع عدم الاتصال للدالة عدم اتصال لانهائي عند للدالة عدم اتصال قفزي عند للدالة عدم اتصال قابل لإزالة x = c إذا تزايدت قيم الدالة أو x = C إذا كانت نهايتا الدالة تناقصت بلا حدود عندما تقترب عندما تقترب x من c من من C من اليمين أو اليسار عند x = C إذا كانت نهاية الدالة عندما تقترب x من C موجودة، اليمين ومن اليسار موجودتين ولا تساوي قيمة الدالة عند ولكنهما غير متساويتين. = x ، ويشار إليها بدائرة صغيرة (٥) غير مظللة؛ لتعبر عن عدم اتصال عند هذه النقطة. وزارة التعليم Ministry of Education 2024-1446 y |y = f(x)| مثال : x C y مثال: 0 x y = f(x) | مثال : |y = f(x) x الفصل 1 تحليل الدوال 26

|y = f(x), f(c) 1 إرشادات للدراسة النهايات: إن وجود قيمة للدالة (f(x عند x = C أو عدم وجودها، لا يؤثر في وجود نهاية للدالة (f(x عندما تقترب تقودنا الملاحظات السابقة إلى اختبار الاتصال الآتي: ملخص المفهوم اختبار الاتصال يقال : إن الدالة ( f ( x متصلة عند x = C إذا حققت الشروط الآتية: • (f(x معرفة عند c ، أي أن (f (c موجودة. X (f(x تقترب من القيمة نفسها عندما تقترب x من c من الجهتين. أي أن (lim f(x موجودة. x-c lim f(x) = f(c) • X-C من . إرشاد تقني جداول : لإنشاء جدول باستعمال الحاسبة البيانية TI-nspire، أدخل الدالة إلى الحاسبة باستعمال قائمة ، ثم اختر تطبيق القوائم وجداول البيانات بالضغط على | . ثم اكتب قيم x للاقتراب من قيمة مثال 1 التحقق من الاتصال عند نقطة حدد ما إذا كانت الدالة 1 - f ( x ) = 2x - 3x متصلة عند 2 = x . برر إجابتك باستعمال اختبار الاتصال. تحقق من شروط الاتصال الثلاثة. 1) هل (2) موجودة؟ 1 = (2)f ، أي أن الدالة معرفة عند 2 = x . (2) هل (lim f(x موجودة؟ x 21 كوّن جدولا يبين قيم (f(x عندما تقترب x من 2 من اليسار واليمين. x 1.9 1.99 1.999 2.0 2.001 2.01 2.1 f(x) 0.52 0.95 0.995 1.005 1.05 1.52 يبين الجدول أنه عندما تقترب قيم x من 2 من اليسار ومن اليمين فإن قيمة (f(x تقترب من 1، أي أن . lim f(x) = 1 x-2 (3) هل (2)lim f(x) = f ؟ f(x) x 2 = 1 ، lium f ( x ، نستنتج أن (2) lim f(x) = f ، إذن الدالة متصلة عند 2 = x. ويوضّح 6 X- بما أن 1 = ( f (2) 6 x-2° منحنى الدالة (f(x في الشكل 1.3.1 اتصال الدالة عند 2 = x . 5 x =2*x^2-3 1.9 1.99 1.999 0.52 0.9502 0.995 2 1 2.001 1.005 حمد B1 =0.52 y 1.05 محددة . (2, 1)- 18 f(x) = 2x2 - 3x - 1 الشكل 1.3.1 تحقق من فهمك حدد ما إذا كانت كل من الدالتين الآتيتين متصلتين عند 0 = x . برر إجابتك باستعمال اختبار الاتصال = } f(x) = { x < 0 (1B x x > 0 وزارة التعليم الدرس 3-1 الاتصال والنهاياتM27 of E 2024-1446 f(x) = x³ (1A

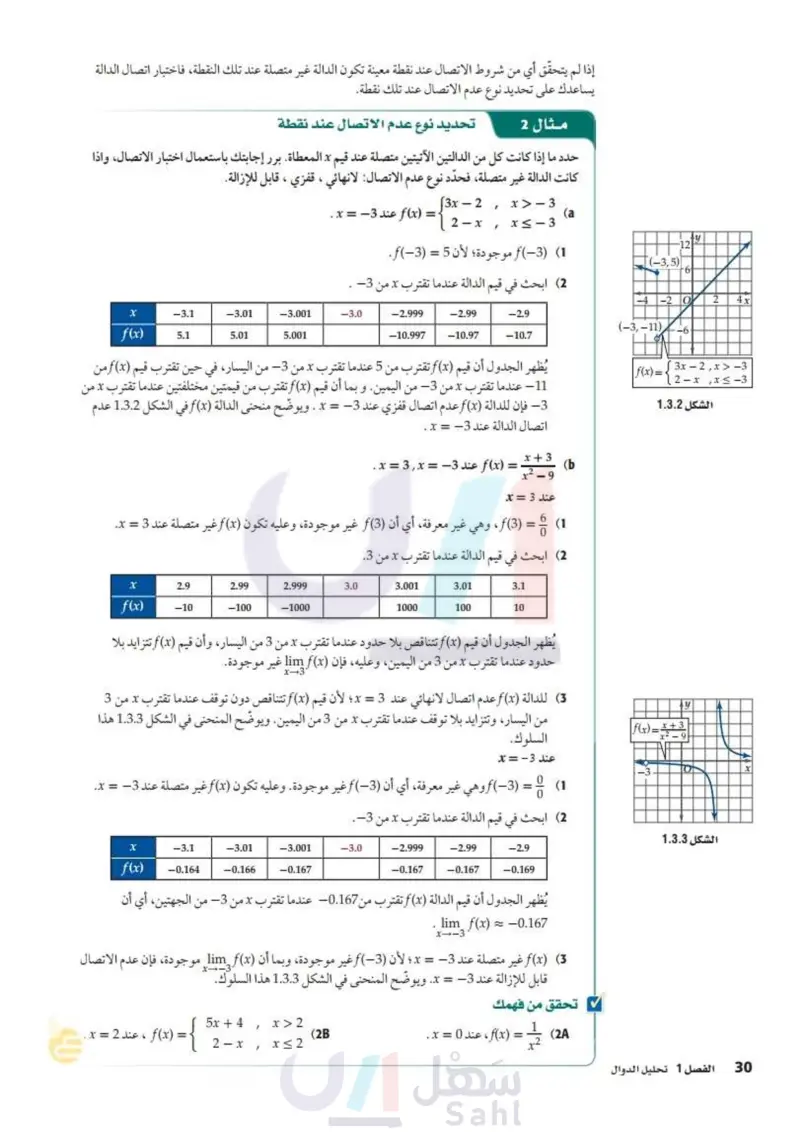
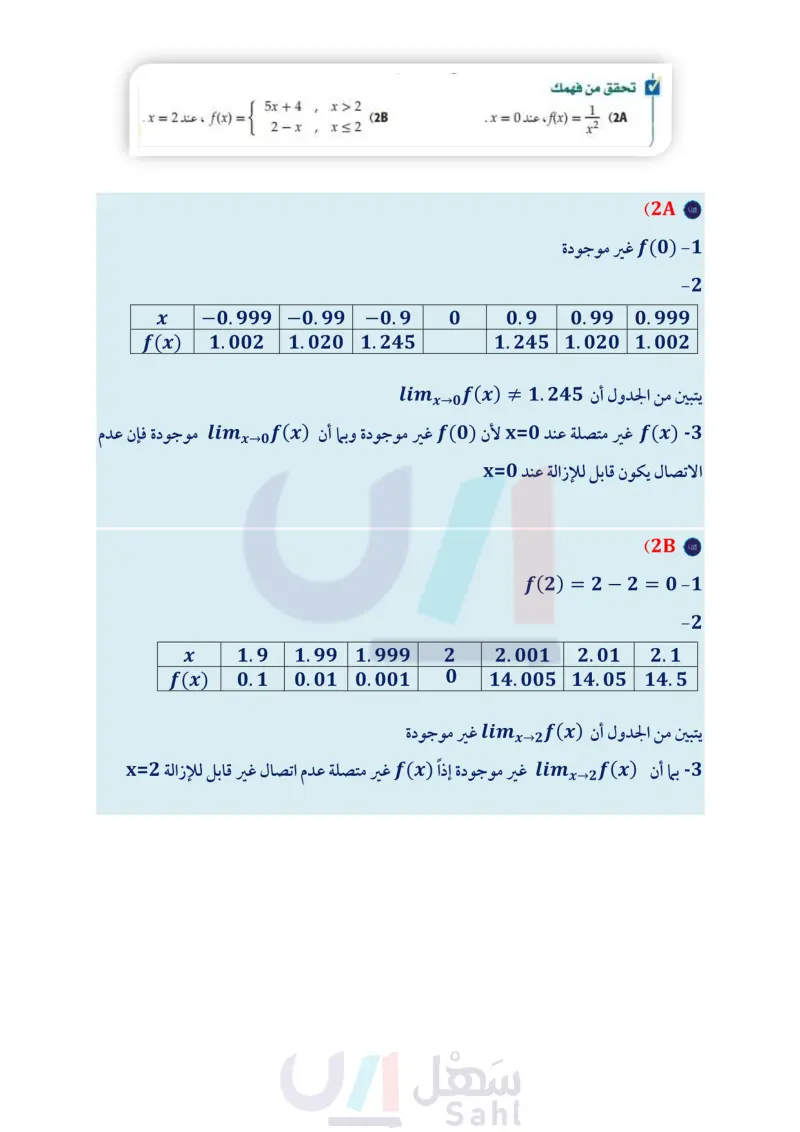
إذا لم يتحقق أي من شروط الاتصال عند نقطة معينة تكون الدالة غير متصلة عند تلك النقطة، فاختبار اتصال الدالة يساعدك على تحديد نوع عدم الاتصال عند تلك نقطة. تحديد نوع عدم الاتصال عند نقطة مثال 2 حدد ما إذا كانت كل من الدالتين الآتيتين متصلة عند قيم x المعطاة . برر إجابتك باستعمال اختبار الاتصال، واذا كانت الدالة غير متصلة، فحدّد نوع عدم الاتصال لانهائي ، قفزي ، قابل للإزالة. (f(x عند 3 = x . √3x-2, = 2-x x > - 3 x≤-3 (a 1) (3)f موجودة؛ لأن 5 = (3)f. (2) ابحث في قيم الدالة عندما تقترب x من 3 . x f(x) -3.1 5.1 -3.01 -3.001 -3.0 5.01 5.001 -2.999 -2.99 -2.9 -10.997 -10.97 -10.7 يُظهر الجدول أن قيم (f(x تقترب من 5 عندما تقترب x من 3 من اليسار، في حين تقترب قيم (f(x من 11- عندما تقترب x من 3 من اليمين. و بما أن قيم (f(x تقترب من قيمتين مختلفتين عندما تقترب x من فإن للدالة (f(x عدم اتصال قفزي عند 3 = x . ويوضح منحنى الدالة (f(x في الشكل 1.3.2 عدم اتصال الدالة عند 3 - = x . = x + 3 x2 - 9 (b (f(x عند 3- = x = 3, x . عند 3 = X 6 1) = (3) f ، و (3)f، وهي غير معرفة، أي أن (3) غير موجودة، وعليه تكون (f(x غير متصلة عند 3 = x. (2) ابحث فى قيم الدالة عندما تقترب x من 3. x 2.9 2.99 2.999 3.0 f(x) -10 -100 -1000 3.001 3.01 3.1 1000 100 10 يُظهر الجدول أن قيم (f(x تتناقص بلا حدود عندما تقترب x من 3 من اليسار، وأن قيم (f(x تتزايد بلا حدود عندما تقترب x من 3 من اليمين وعليه فإن (lim f(x غير موجودة. x-3° 3 للدالة ( f ( x عدم اتصال لانهائي عند 3 = x ؛ لأن قيم (f(x تتناقص دون توقف عندما تقترب x من 3 من اليسار، وتتزايد بلا توقف عندما تقترب x من 3 من اليمين. ويوضّح المنحنى في الشكل 1.3.3 هذا السلوك. عند 3 - =x Ay 12 (-3,5) 6 -4-20 2 4x (-3,-11) -6 | f(x)= 3x2, x> -3 2-x, x-3 الشكل 1.3.2 |f(x) = x+3 x2 - 9 -3 y 1) = (3) f وهي غير معرفة، أي أن (3) fغير موجودة. وعليه تكون (f(x غير متصلة عند 3 = x. (2) ابحث في قيم الدالة عندما تقترب x من 3 . الشكل 1.3.3 x -3.1 -3.01 f(x) -0.164 -0.166 -3.001 -0.167 -3.0 -2.999 -0.167 -2.99 -0.167 -2.9 -0.169 يُظهر الجدول أن قيم الدالة (f(x تقترب من 0.167- عندما تقترب x من 3 من الجهتين، أي أن lim, f(x) ~ - 0.167 x-3 (3) (f(x غير متصلة عند -3 = x ؛ لأن (3) أغير موجودة ، وبما أن (lim, f(x) موجودة، فإن عدم الاتصال = x-3 قابل للإزالة عند 3 = x ويوضّح المنحنى في الشكل 1.3.3 هذا السلوك. (f(x ، عند 2 = x . f(x) = { x > 2 5x+4 (2B 2- x, x ≤ 2 وزارة التعليم Ministry of Education 2024-1446 تحقق من فهمك (28) 1 = (f(x ، عند 0 = x . x2 الفصل 1 تحليل الدوال 8 28

حالة لاحظ أنه في عدم الاتصال القابل للإزالة؛ يمكن إعادة تعريف الدالة لتصبح متصلة عند تلك النقطة. وفي هذه الحالة تكون النهاية عند x = c موجودة، ولكن الدالة غير معرفة عند x = c أو أن (f (c لا تساوي قيمة نهاية الدالة عند x = C . كما في الشكل المجاور. y = f(x)| x C يصنف كل من عدم الاتصال اللانهائي وعدم الاتصال القفزي على أنهما عدم اتصال غير قابل للإزالة؛ لأنه لا يمكن إعادة تعريف الدالة لتصبح متصلة عند تلك النقطة، حيث إن قيم الدالة تقترب من قيم مختلفة إلى يمين نقطة عدم الاتصال وإلى يسارها، أو أن قيم الدالة لا تقترب من قيمة محدّدة عند هذه النقطة، أي تزداد قيم الدالة أو تتناقص بلا حدود. مثال 3 أعد تعريف الدالة إزالة عدم الاتصال x2 - 16 X- - 4 = (f(x؛ لتصبح متصلة عند 4 = x . 1 = (4)f، أي أن (4)f غير موجودة. (2) ابحث في قيم الدالة عندما تقترب x من 4. X 3.9 3.99 3.999 4.0 4.001 4.01 4.1 f(x) 7.9 7.99 7.999 8.001 8.01 8.1 x-4° يظهر الجدول أعلاه أن قيم (f(x تقترب من 8 عندما تقترب x من 4 من الجهتين، أي أن 8 = (lim f(x (f(x غير متصلة عند 4 = x؛ لأن (4) غير موجودة، وبما أن (lim f(x موجودة، فإن عدم الاتصال قابل للإزالة عند 4 = x x-4° (4) بما أن عدم الاتصال قابل للإزالة عند 4 = x ، لذا أعد تعريف الدالة لتصبح f(x) x2 - 16 = 4 ,x4 x 8 ,x = 4 لاحظ أن هذه الدالة أصبحت متصلة عند 4 = x؛ لأن (4) f موجودة وتساوي 8 تحقق من فهمك - x 3) أعد تعريف الدالة 1 - 1 = (f(x ؛ لتصبح متصلة عند 1 = x . x-1 تستعمل نظرية القيمة المتوسطة ونتيجتها لتقريب أصفار الدوال المتصلة على فترة مغلقة، حيث تكون الدالة f متصلة على (a)، إذا كانت متصلة عند كل نقطة تنتمي إلى هذه الفترة، وتكون متصلة على ] إذا كانت متصلة عند كل من نقاطها، وكانت متصلة من اليمين عند (lim f(x) (fa ) ، ومتصلة من اليسار عند b ((lim _ f(x) = f(b) . ومن الجدير بالذكر أن الدوال الكثيرة الحدود والجذرية والنسبية، تكون متصلة على مجالها نقطة x→b xa+ (b,f(b)) f(b) f(c) (c, n) O a " f(a) C b (a,f(a)) وزارة التعليم الدرس 3-1 - الاتصال والنهايات of 29 2024-1446 نظرية القيمة المتوسطة X دائما . نظرية إذا كانت (f(x دالة متصلة على [a,b]، وكانت a < b ووجدت قيمة n بين (f (a و (f (b فإنه يوجد عدد C بين a و b ، بحيث f(c) = n. نتيجة (موقع صفر الدالة ) : إذا كانت (f(x دالة متصلة وكان (f (a و (f(b) مختلفين في الإشارة فإنه يوجد عدد واحد على الأقل C بين a و b ، بحيث 0 = (f (c . أي يوجد صفر للدالة بين a و b .

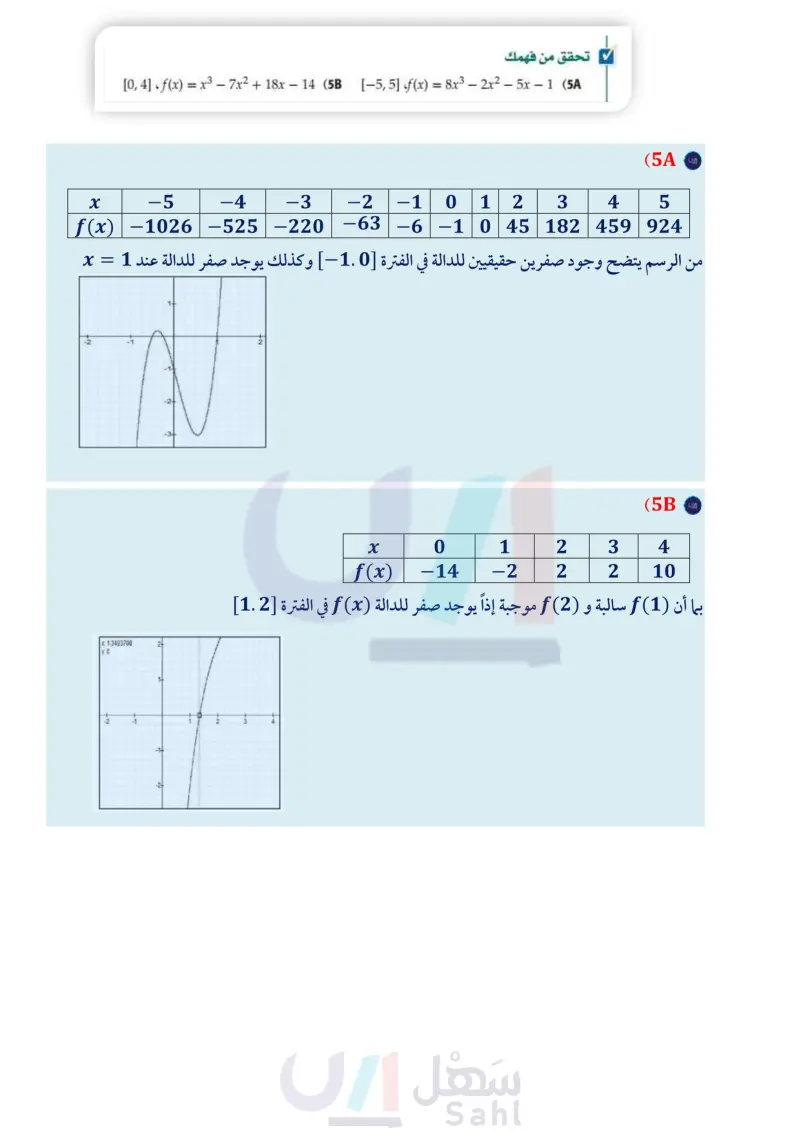
مثال 4 تقريب الأصفار عند تغيير الإشارة حدد الأعداد الصحيحة المتتالية التي تنحصر بينها الأصفار الحقيقية للدالة 2 + f(x) = x 3 - 4x في الفترة [44] . x -4 -3 -2 -1 0 1 2 3 4 f(x) -13 -46 2 5 2 -1 2 17 50 بی y 20 2 X | f(x) = x3 - 4x + 2 الشكل 1.3.4 تعلم أن الدالة متصلة على [-]؛ لأنها كثيرة حدود، وبما أن (3) f سالبة و (2)f موجبة، وبحسب النتيجة السابقة، فإنه يوجد صفر للدالة ( f ( x بين - - . لاحظ أن قيم الدالة تتغير إشاراتها أيضًا في الفترة 1 > x > 0 وفي الفترة 2 > x > 1 . وهذا يدل على أن الأصفار الحقيقية للدالة تنحصر بين العددين 3 و 2 ، والعددين 0 و 1 والعددين 1 و 2. ويوضح منحنى الدالة (f(x في الشكل 1.3.4 هذه النتيجة. تحقق من فهمك [-3, 4] f(x) = = x2 - 6 X + 4 (4B [-6, 4] ،f(x) = x3 + 2x2 - 8x + 3 (4 إن تغير إشارات قيم الدالة في فترة ما يحدّد موقعاً تقريبيًّا لصفر الدالة الحقيقي. أما الفترات التي لا تتغير فيها الإشارة فإنها لا تنفي وجود أصفار للدالة، ويُعد تمثيل الدالة من أفضل طرق التحقق مثال 5 تقريب الأصفار دون تغير الإشارة ذلك. من حدد الأعداد الصحيحة المتتالية التي تنحصر بينها الأصفار الحقيقية للدالة 0.16 + f(x) = x2 + x -3- -2- 1 -2 -1 إرشاد تقني قد يُظهر التمثيل البياني للدالة صفرًا واحدًا؛ لذا اختر التدريج المناسب لترى جميع أصفار الدالة بوضوح. في الفترة [3] x -3 -2 -1 0 1 2 3 f(x) 6.16 2.16 0.16 0.16 2.16 6.16 12.16 y - | f(x) = x2 + x + 0.16 1 2 تعلم أن الدالة متصلة على [3] ؛ لأنها كثيرة حدود، وأن قيمها لا تغير إشارتها عند قيم x المعطاة ، ولكن ( f ( x تتناقص عندما تقترب قيم x العدد 1 من اليسار، وتبدأ (f(x بالتزايد عن يمين ) 0 = x ؛ لذا فإن من المحتمل وجود صفر حقيقي للدالة بين العددين المتتاليين 1 و 0. مثل الدالة بيانيا للتحقق من ذلك. من يقطع منحنى الدالة المحور x مرتين في الفترة [1]؛ لذا فإنه يوجد صفرين حقيقيين للدالة في هذه الفترة. تحقق من فهمك [0, 4] ، f(x) = x3 - 7x2 + 18x - 14 (5 [5, 5] ،f(x) = 8x3 - 2x2 - 5x - 1 (5 قراءة الرياضيات النهايات: تقرأ العبارة (lim f(x x1x نهاية (f(x عندما تقترب x من موجب ما لانهاية. وتقرأ العبارة (lim f(x نهاية 811X (f(x عندما تقترب x من سالب ما لانهاية. إرشاد: استعمل الآلة الحاسبة البيانية إذا لزم الأمر) سلوك طرفي التمثيل البياني : يصف سلوك طرفي التمثيل البياني شكل الدالة عند طرفي منحناها، أي أنه يصف قيم (f(x عندما تزداد قيم x أو تنقص بلا حدود، أي عندما تقترب x من أو - - . ولوصف سلوك طرفي التمثيل البياني يمكنك استعمال مفهوم النهاية. سلوك طرف التمثيل البياني من اليسار x-f(x) lim f(x) أحد إمكانات سلوك طرفي التمثيل البياني هو زيادة قيم (f(x أو نقصانها دون حدود. ويمكن وصف هذا السلوك بأن (f(x تقترب من موجب ما لانهاية أو من سالب ما لانهاية على الترتيب. 1 سلوك طرف التمثيل البياني من اليمين 81x 88 x = -∞ lim f(x) y = f(x)| lim f(x) f(x) X→X 818 81X lim f(x) : = ∞ f(x) 811X 0 - X وزارة التعليم Ministry of Education 2024-1446 الفصل 1 تحليل الدوال 30

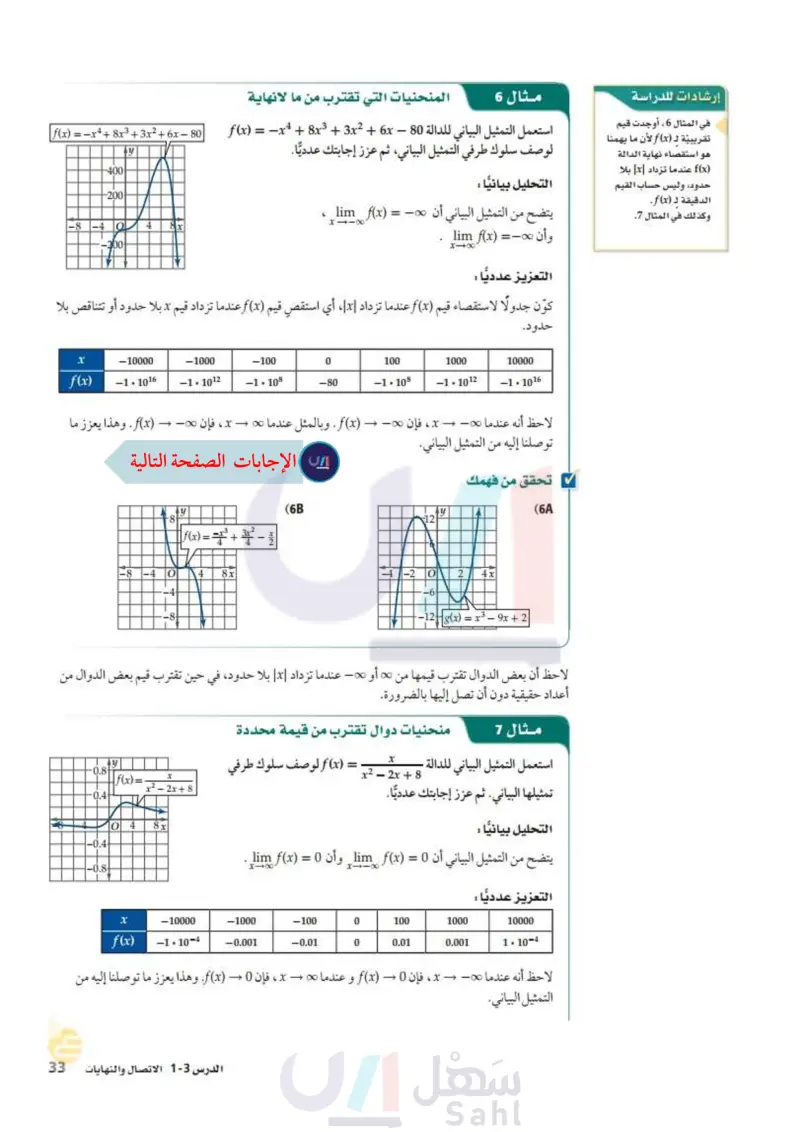
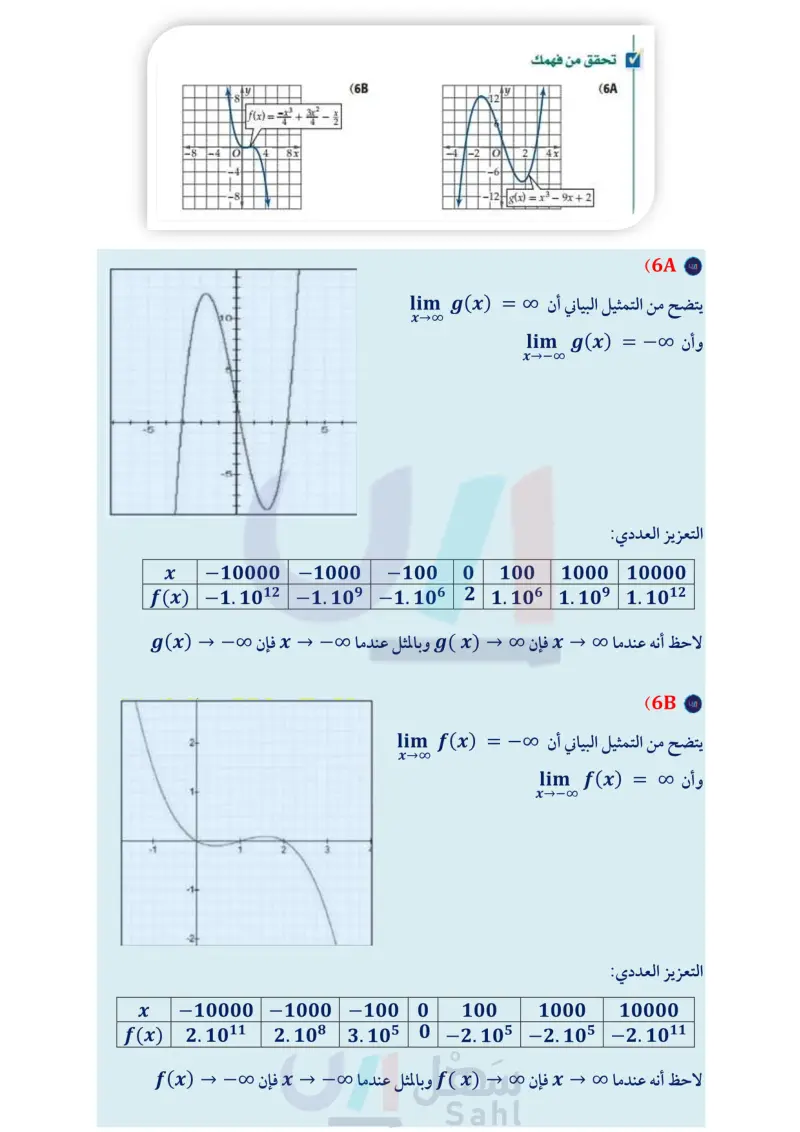
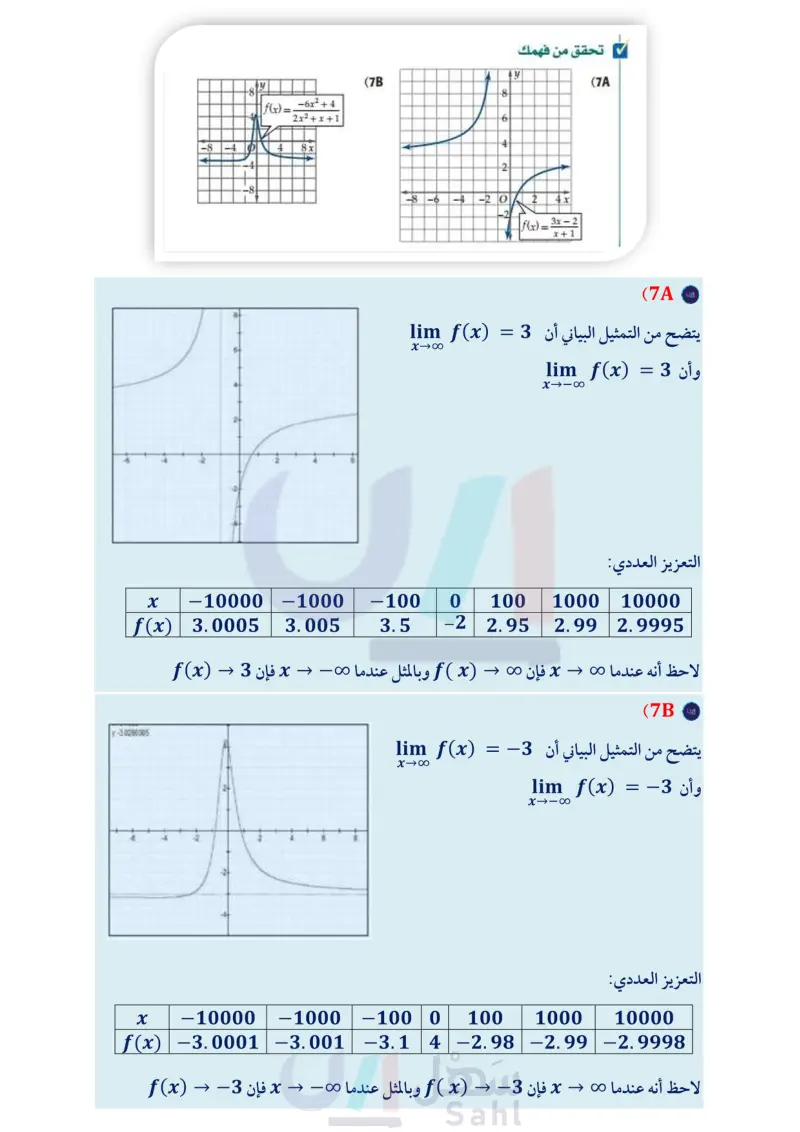
(f(x) =-x+8x3+3x²+6x-80 -400- -200- y إرشادات للدراسة في المثال 6 ، أوجدت قيم تقريبية لـ (f(x لأن ما يهمنا هو استقصاء نهاية الدالة (f(x عندما تزداد || بلا حدود، وليس حساب القيم الدقيقة لـ (f(x. وكذلك في المثال 7. مثال 6 المنحنيات التي تقترب من ما لانهاية استعمل التمثيل البياني للدالة 80 - f(x) = x4 + 8x3 + 3x2 + 6x لوصف سلوك طرفي التمثيل البياني، ثم عزز إجابتك عدديًا. التحليل بيانيا : يتضح من التمثيل البياني أن xlima f(x) = - oo ، lim_f(x) -8 -4 O -200 4 8x lim f(x) = == XX وأن - التعزيز عدديًا : كون جدولًا لاستقصاء قيم (f(x عندما تزداد x أي استقص قيم (f(x عندما تزداد قيم x بلا حدود أو تتناقص بلا حدود. x -10000 -1000 f(x) -1.1012 -1.1016 -100 -1.108 0 100 1000 10000 -80 -1.108 −1·1012 -1.1016 لاحظ أنه عندما - x ، فإن - → - (f(x . وبالمثل عندما x + o ، فإن 00 + (f(x . وهذا يعزز ما توصلنا إليه من التمثيل البياني. تحقق من فهمك -8 -4 y -8- f(x) = = 1³ + 3x² - 82 2 10+ -8 4 ++ 8x (6B 12 به -4-2 O 2 4x 10 --12 g(x) = x³- 9x+2 (6 لاحظ أن بعض الدوال تقترب قيمها من 0 أو - عندما تزداد || بلا حدود، في حين تقترب قيم بعض الدوال من أعداد حقيقية دون أن تصل إليها بالضرورة. منحنيات دوال تقترب من قيمة محددة مثال 7 استعمل التمثيل البياني للدالة x x2 - 2x + 8 = (f(x لوصف سلوك طرفي y 0.8 |f(x) = X = x2 - 2x + 8 0.4 -0.4 -0.8 04 8x تمثيلها البياني. ثم عزز إجابتك عدديًّا. التحليل بيانيا : يتضح من التمثيل البياني أن 0 = (lim f(x وأن 0 = (lim f(x X11X XxX التعزيز عدديًا : x f(x) -10000 −1.10-4 -1000 -0.001 -100 0 100 1000 10000 -0.01 0 0.01 0.001 1.10-4 لاحظ أنه عندما x + o ، فإن 0 - ( f ( x و عندما x + o ، فإن 0+ ( f ( x وهذا يعزز ما توصلنا إليه من - →> - . وزارة التعليم الدرس 3-1 الاتصال والنهاياتM31y of E 2024-1446 التمثيل البياني.

-8 -4 y 8 | f(x) = . -6x²+4 2x2 + x + 1 4 8x + -8 تحقق من فهمك y (7B 8 6 4 ہے 2 -8-6-4 -20 2 4x f(x) = = 3x-2 x + 1 (7A إن معرفة سلوك طرفي التمثيل البياني يساعد على حل بعض المسائل الحياتية. مثال 8 من واقع الحياة تطبيقات سلوك طرفي التمثيل البياني فيزياء : تُعطى قيمة طاقة الوضع الناتجة عن الجاذبية الأرضية لجسم بالقاعدة GmMe = r (r) ، حيث G ثابت نيوتن للجذب الكوني، و m كتلة الجسم، و Me كتلة الأرض ، و r المسافة بين الجسم ومركز الأرض كما في الشكل المجاور . ماذا يحدث لطاقة الوضع الناتجة عن الجاذبية الأرضية لجسم عندما يتحرك مبتعدا عن الأرض مسافة كبيرة جدًا؟ Me m المطلوب من المسألة وصف سلوك طرف التمثيل البياني لـ (r) عندما تزداد قيم r كثيرًا، أي إيجاد (lim U(r 1 x وبما أن كلا من Me , ثوابت، فإن ناتج الضرب GmM عدد ثابت أيضًا. وعندما تزداد قيم r فإن قيمة GmMe r ' e 188 الكسر . تقترب من الصفر؛ لذا فإن 0 = lim Ur ، ومن ثم إذا تحرك جسم مبتعدا عن الأرض بصورة كبيرة، فإن طاقة الوضع الناتجة عن الجاذبية الأرضية لهذا الجسم تقترب من الصفر . تحقق من فهمك pv² q(v) = 2 8) فيزياء: الضغط الديناميكي هو قياس الضغط الناتج عن حركة جزيئات الغاز ويعطى بالقاعدة حيث p ( ويقرأ روه كثافة الغاز ، و السرعة التي يتحرك بها الجزيء . ماذا يحدث للضغط الديناميكي لجزيئات الغاز عندما تستمر سرعة الجزيئات في التزايد؟ وزارة التعليم Ministry of Education 2024-1446 الربط مع الحياة غالبًا ما تستعمل العلاقة GmMe r (r) لإيجاد طاقة الوضع الناتجة عن الجاذبية الأرضية لقياس السرعة المطلوبة للتخلص من الجاذبية الأرضية وهي. . 25000 mi/h الفصل 1 تحليل الدوال 32

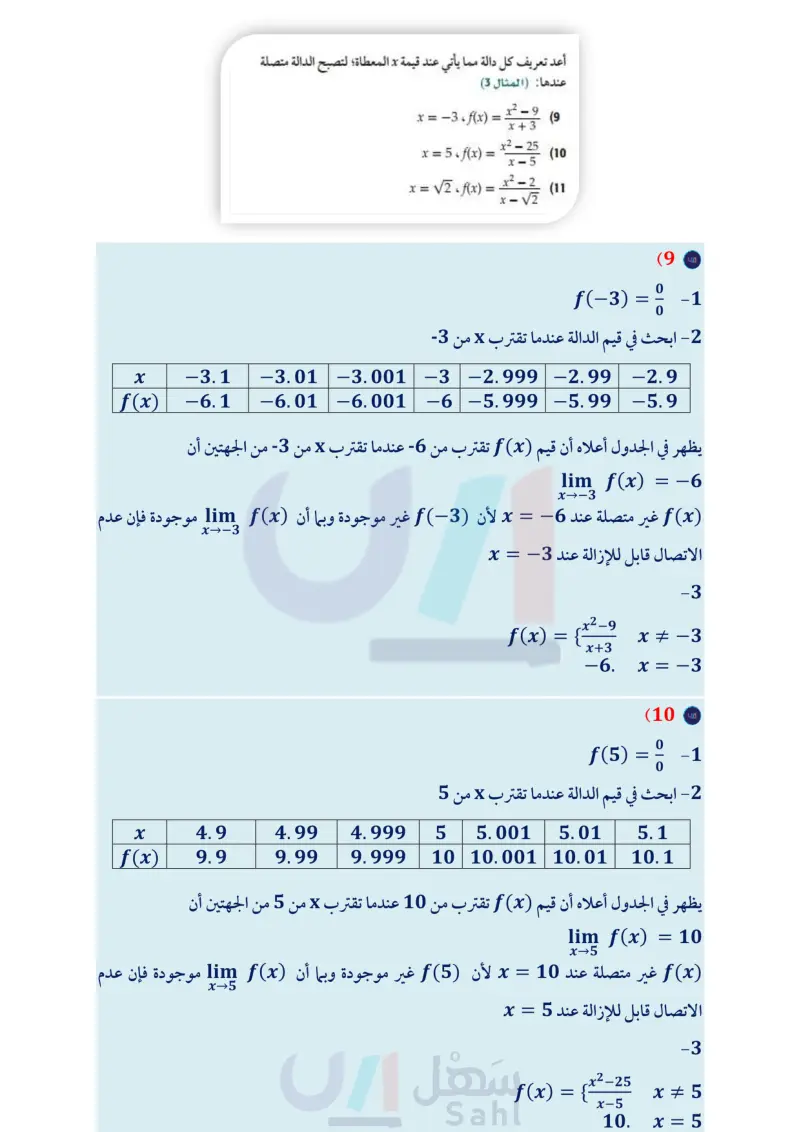
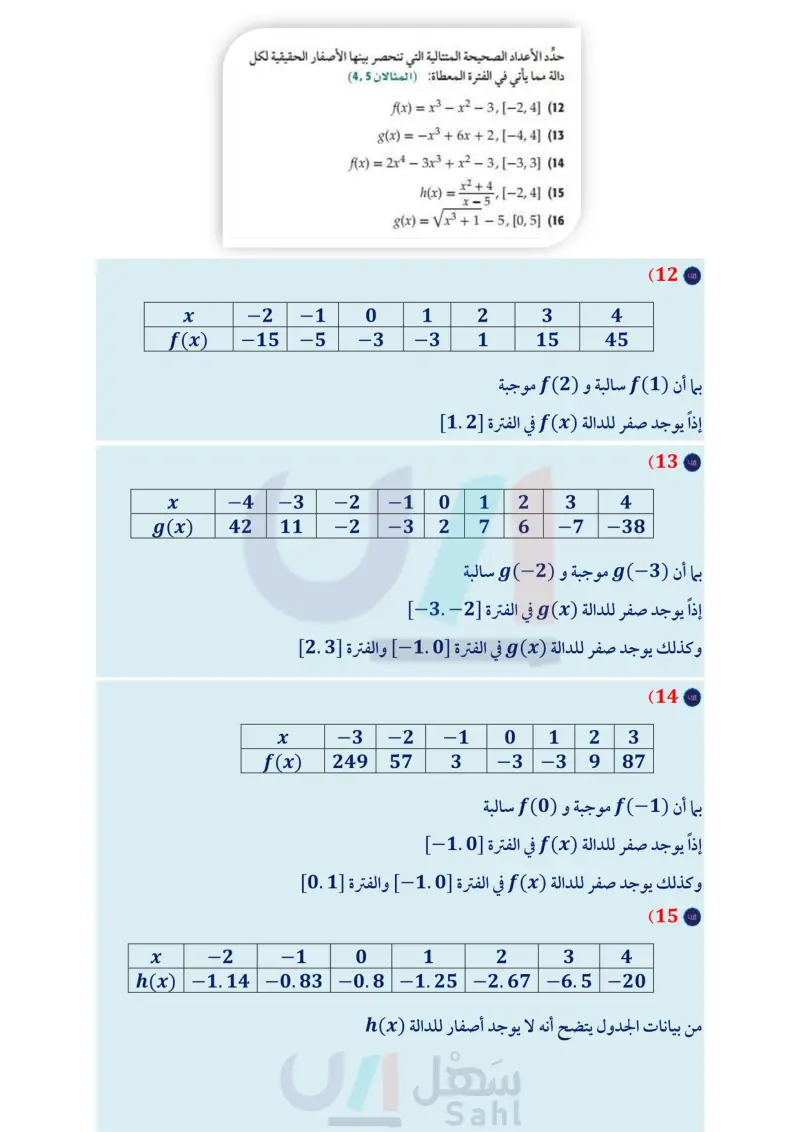
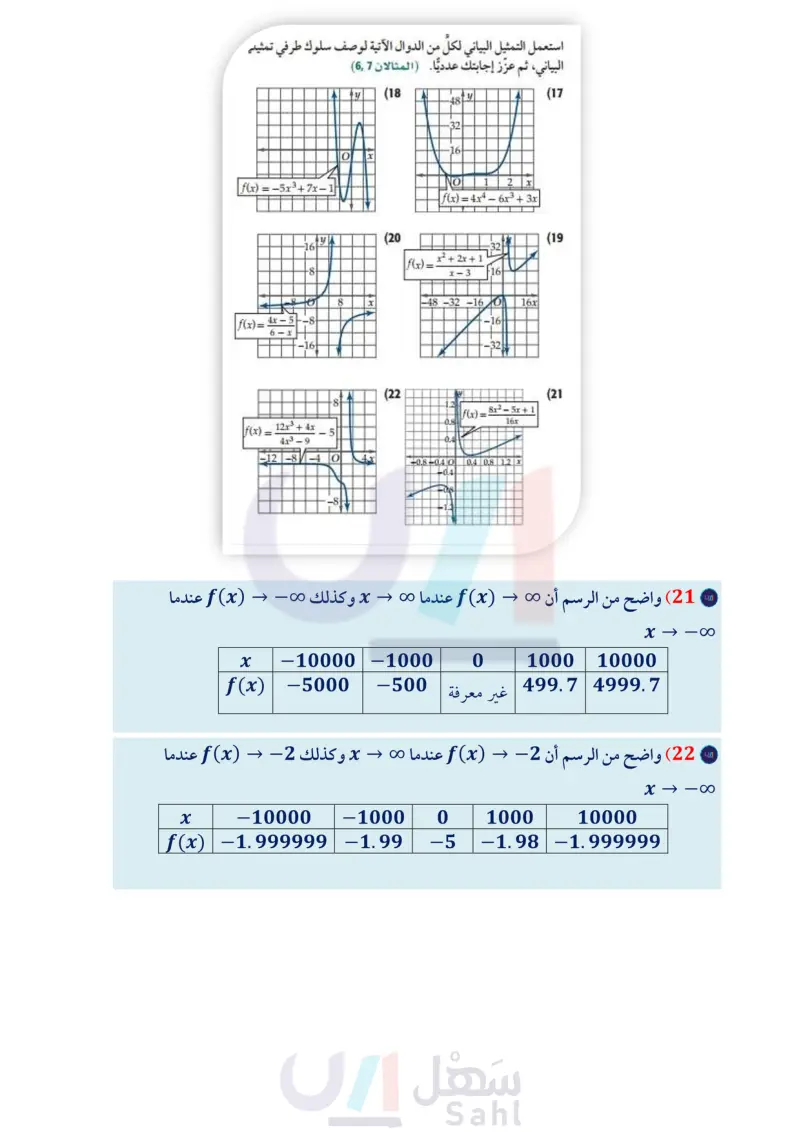
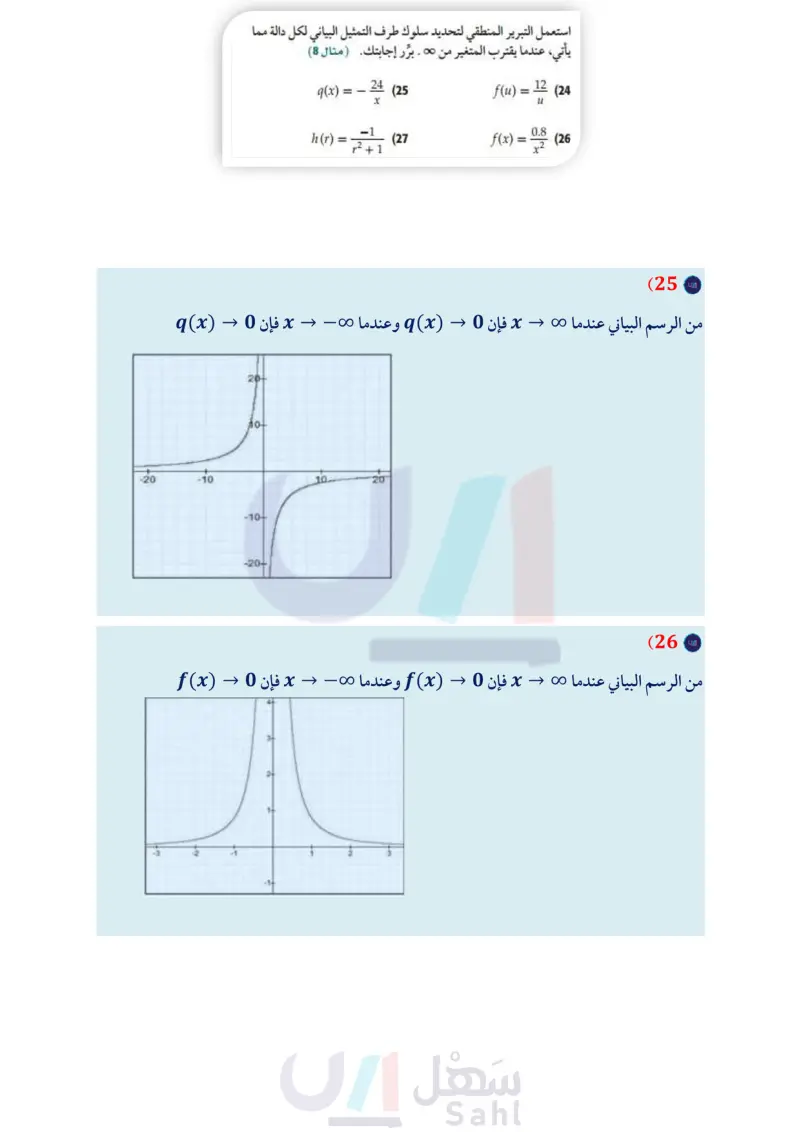
تدرب وحل المسائل استعمل التمثيل البياني لكلِّ من الدوال الآتية لوصف سلوك طرفي تمثيلها حدد ما إذا كانت كل دالة مما يأتي متصلة عند قيمة x المعطاة. وبرّر البياني، ثم عزّز إجابتك عدديًّا (المثالان 67) إجابتك باستعمال اختبار الاتصال. وإذا كانت الدالة غير متصلة فحدّد نوع عدم الاتصال : لانهائي قفزي قابل للإزالة المثالان (1) 1) 4 - f(x) = Vx2 ، عند 5 = x . - 2) 5 + f(x) = Vx ، عند 8 = x . (17 y (18 48 y 32 9 -16 x 6 (x) ، عند 6 - = x = 6, x . (x) ، عند 1 = x . = x2 - 36 x + 6 (3 x = (4 x 1 x-4 (5 x2 – 5x + 4 x2 - 6x = (6 .3 = (x) ، عند 1 = x = 4,x . (x) ، عند 0 = x = 6, x . 6 4x-1 ' x≤-6 (7 -x+2 x > 6 ' } = (f(x ، عند 6 - = x . 8) فيزياء: غرفتان درجتا حرارتهما مختلفتان يفصل بينهما حائط . تنتقل الحرارة بين الغرفتين عبر الحائط بحسب 7.4 العلاقة f(to) = i، حيث تمثل غرفة دافئة غرفة باردة 80°F حائط 60°F (f (to المعدل الزمني لانتقال الحرارة بالواط، و 70 سمك الحائط بالمتر المثالان 1,2) (a) حدد ما إذا كانت الدالة متصلة عند 0.4 = 20. وبرّر إجابتك باستعمال اختبار الاتصال. الاتصال للدالة (إن وجدت)، وما نوعه؟ عدم ا حدد نقاط مثل الدالة بيانيا للتحقق مما توصلت إليه في الفرع b . أعد تعريف كل دالة مما يأتي عند قيمة x المعطاة؛ لتصبح الدالة متصلة عندها المثال (3) O 1 2 X f(x) = 4x4 - 6x3 + 3x |f(x) = −5x³+7x-1 3 y (20 (19 16 32 | f(x) x2 + 2x + 1 -8 x-3 16 8 x 48 -32 -160 16x |f(x)=. 4x-5 -8 -16 6-x -16 -32 (22 y (21 00 1.2 |f(x) = 8x2_ = f(x) 12x3 + 4x 0.8 - 5x+1 16x = ما 5 4x3 9 0.4 -12 -8 -40 4x -0.8 -0.4 0 -0.4 0.4 0.8 1.2 x -0.8 (23 كيمياء: يعطى معدل التفاعل R في تجربة كيميائية بالدالة 0.5x = x + 12 (x) ، حيث x تركيز المحلول بالملجرام لكل لتر . (مثال (7) x = 5 ، f(x) = x = −3. f(x) = 6 x2 - 9 x + 3 (9 x2 – 25 (10 x-5 x = V2 ، f(x) = x2 2 (11 Xx V2 حدد الأعداد الصحيحة المتتالية التي تنحصر بينها الأصفار الحقيقية لكل دالة مما يأتي في الفترة المعطاة المثالان (45) مثل الدالة بيانيًا باستعمال الحاسبة البيانية. صف سلوك طرفي التمثيل البياني، وماذا يعني في التجربة؟ عزّز إجابتك عدديًا. استعمل التبرير المنطقي لتحديد سلوك طرف التمثيل البياني لكل دالة مما يأتي، عندما يقترب المتغير من ∞ . برر إجابتك ( مثال 8) 12 (24 u = f(u) = f(x) = 0.8 = (26 1-2 9(x) = - 24 x (25 −1 h(r) = (27 p2 + 1 f(x) = x3 - x2 - 3, [-2, 4] (12 g(x) = −x³ + 6x + 2, [−4,4] (13 f(x) = 2x4 - 3x3 + x2 - 3, [33] (14 h(x) = x²+4, [−2, 4] (15 X- 5 (x) = Vx3 + 1 - 5, [0, 5] (16 (28) فيزياء : تُعطى طاقة الحركة لجسم متحرك بالدالة .E(m) = p2 2m حيث p الزخم حاصل ضرب كتلة الجسم في سرعته المتجهة)، m كتلة الجسم. إذا وضع رمل في شاحنة متحركة، فماذا سيحدث إذا استمرت m في الازدياد؟ (مثال 8 ) وزارة التعليم الدرس 3-1 الاتصال والنهاياتM33 of E 2024-1446

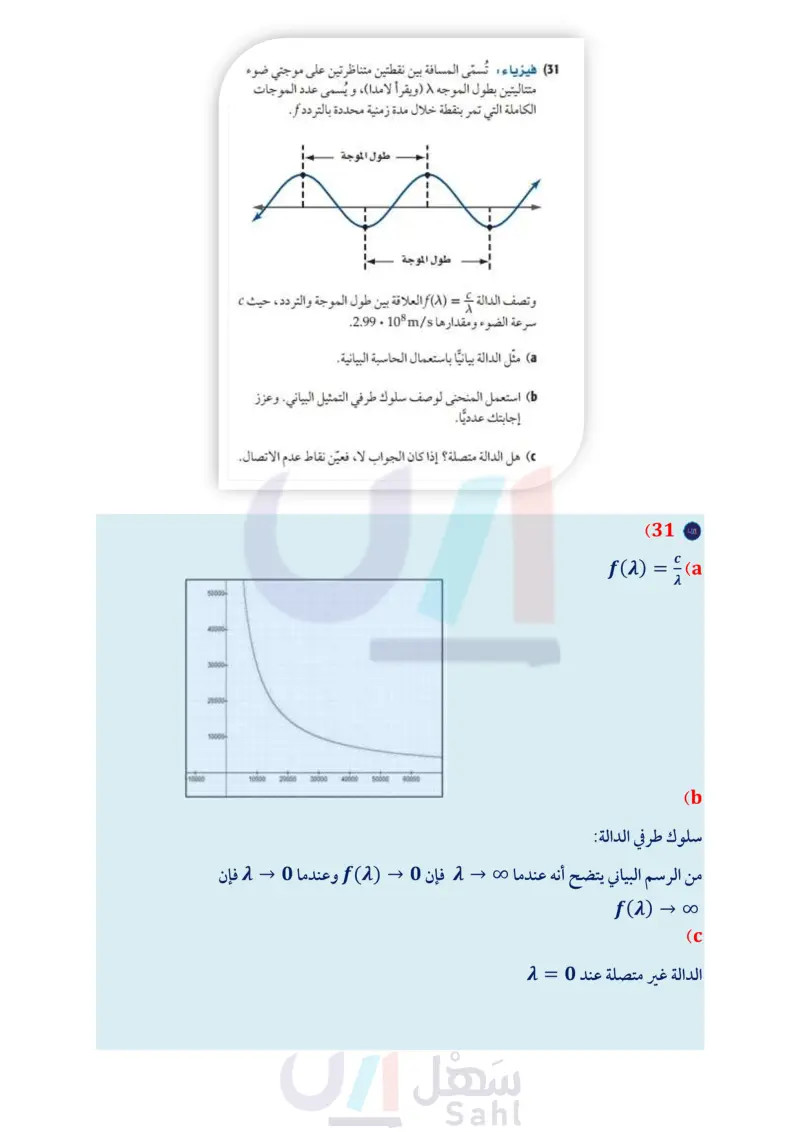
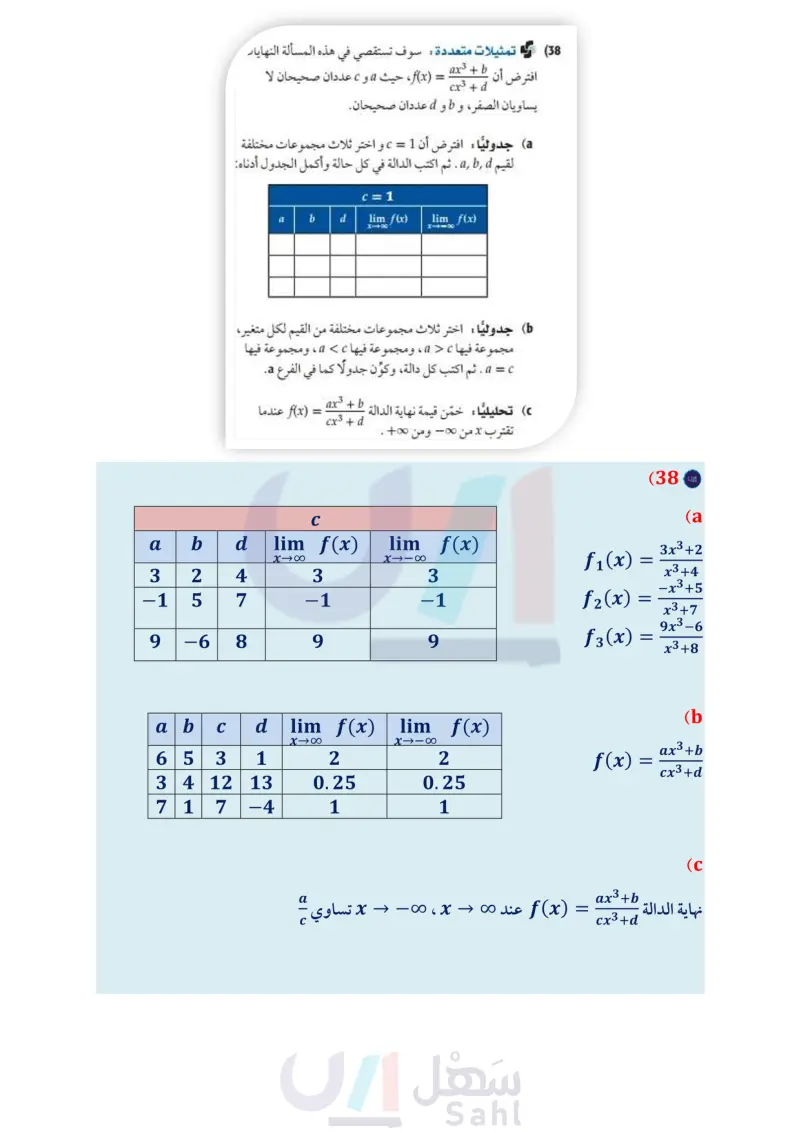
استعمل كلا من التمثيلين البيانيين الآتيين لتحديد قيمة أو قيم x التي تكون الحاسبة البيانية : مثل بيانيًّا كلَّا من الدوال الآتية وصف سلوك طرفي الدالة غير متصلة عندها، وحدد نوع عدم الاتصال، ثم استعمل المنحنى التمثيل البياني، وعزز إجابتك عدديًا. لوصف سلوك طرفي التمثيل البياني. برر إجابتك. g(x) = x5 - 20x4 + 2x3 - 5 (35) - (30 f(x) = 16x2 12 (36 19 g ( x ) = 2x - 1 1 - x (29 له 2 x2 + 15x -8 h(x) 15 11x2 201 2 2 4X - 40 - 4- 8 4 12x 31 فيزياء: تُسمّى المسافة بين نقطتين متناظرتين على موجتي ضوء متتاليتين بطول الموجه ) ويقرأ لامدا) ، و يُسمى عدد الموجات الكاملة التي تمر بنقطة خلال مدة زمنية محددة بالتردد f. λ طول الموجة طول الموجة وتصف الدالة - = (۸) f العلاقة بين طول الموجة والتردد، حيث c سرعة الضوء ومقدارها m/s 108 . 2.99. a مثل الدالة بيانيًا باستعمال الحاسبة البيانية. استعمل المنحنى لوصف سلوك طرفي التمثيل البياني. وعزز إجابتك عدديًّا. هل الدالة متصلة ؟ إذا كان الجواب لا، فعيّن نقاط عدم الاتصال. الحاسبة البيانية : مثل كلَّا من الدوال الآتية بيانيا، ثم حدد ما إذا كانت متصلة أم لا. وإذا كانت غير متصلة، فحدد نوع عدم الاتصال، وحدد نقاطه. ثم صف سلوك طرفي التمثيل البياني، وعين أصفار الدالة إن وجدت. (32 x2 x3 – 4x2 + x + 6 f(x) = (37) أعمال: بدأ حمد مشروعًا تجاريًا صغيرًا بالطباعة على القمصان وبيعها . إذا كانت تكلفة الطباعة على القميص الواحد 9 ريالات وتكلفة المعدات اللازمة 12000 ريال. فأجب عما يأتي: a اكتب دالة تبين معدّل تكلفة الطباعة على القميص الواحد على صورة دالة في عدد القمصان المنتجة .. استعمل الحاسبة البيانية لتمثيل الدالة. إذا استمر ازدياد عدد القمصان المنتجة بشكل كبير، فكم سيصبح معدل تكلفة الطباعة على القميص الواحد؟ (38) تمثيلات متعددة : سوف تستقصي في هذه المسألة النهايات. أن ax3 + b cx3 + d = افترض (f(x حيث a و c عددان صحيحان لا يساويان الصفر، و b و d عددان صحيحان. a جدوليًا : افترض أن 1 = c و اختر ثلاث مجموعات مختلفة لقيم . ثم اكتب الدالة في كل حالة وأكمل الجدول أدناه: lim_f(x) 811X c = 1 a b d lim_f(x) 81x جدوليا : اختر ثلاث مجموعات مختلفة من القيم لكل متغير، 6 مجموعة فيها a c ، ومجموعة فيها > a ، ومجموعة فيها a = c . ثم اكتب كل دالة، وكون جدولا كما في الفرع a. تحليليا : خمّن قيمة نهاية الدالة تقترب x من - ومن too ax3 + b cx3 + d = (f(x عندما وزارة التعليم Ministry of Education 2024-1446 4x2 + 11x - 3 h(x) = (33 x2 + 3x – 18 x3 5x2 – 26x + 120 h(x) = (34 x2 + x – 12 الفصل 1 تحليل الدوال 34

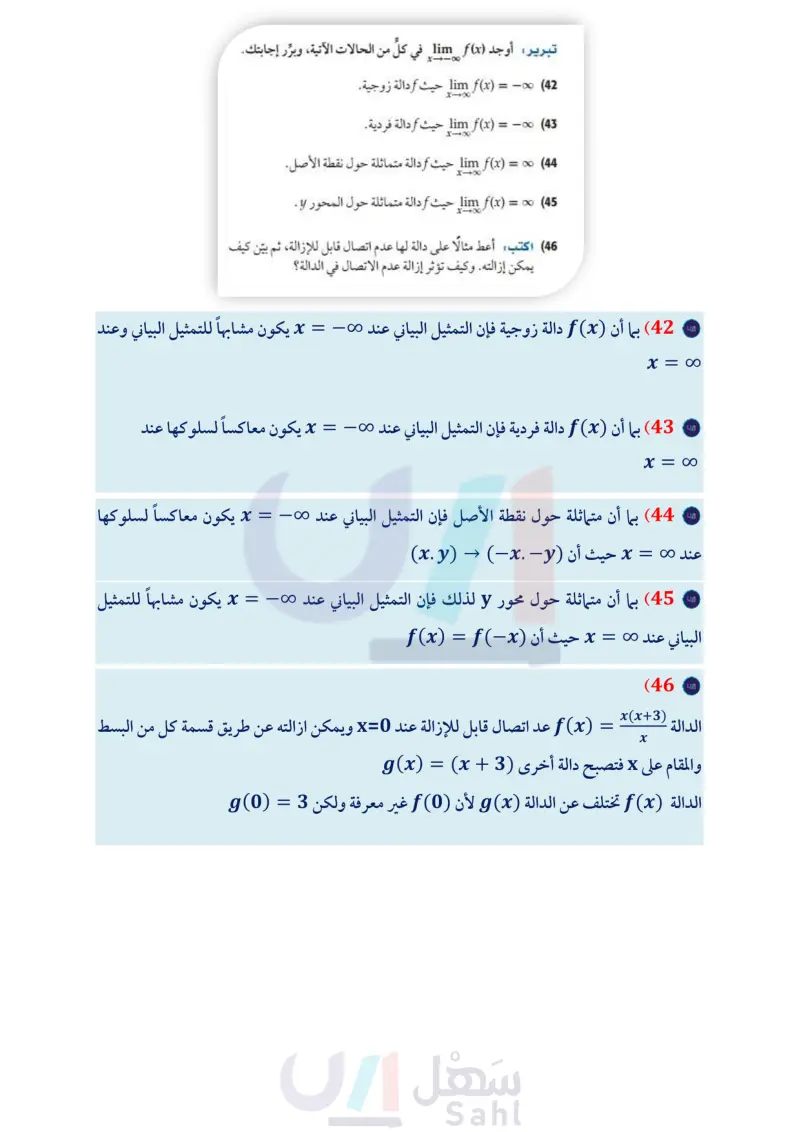
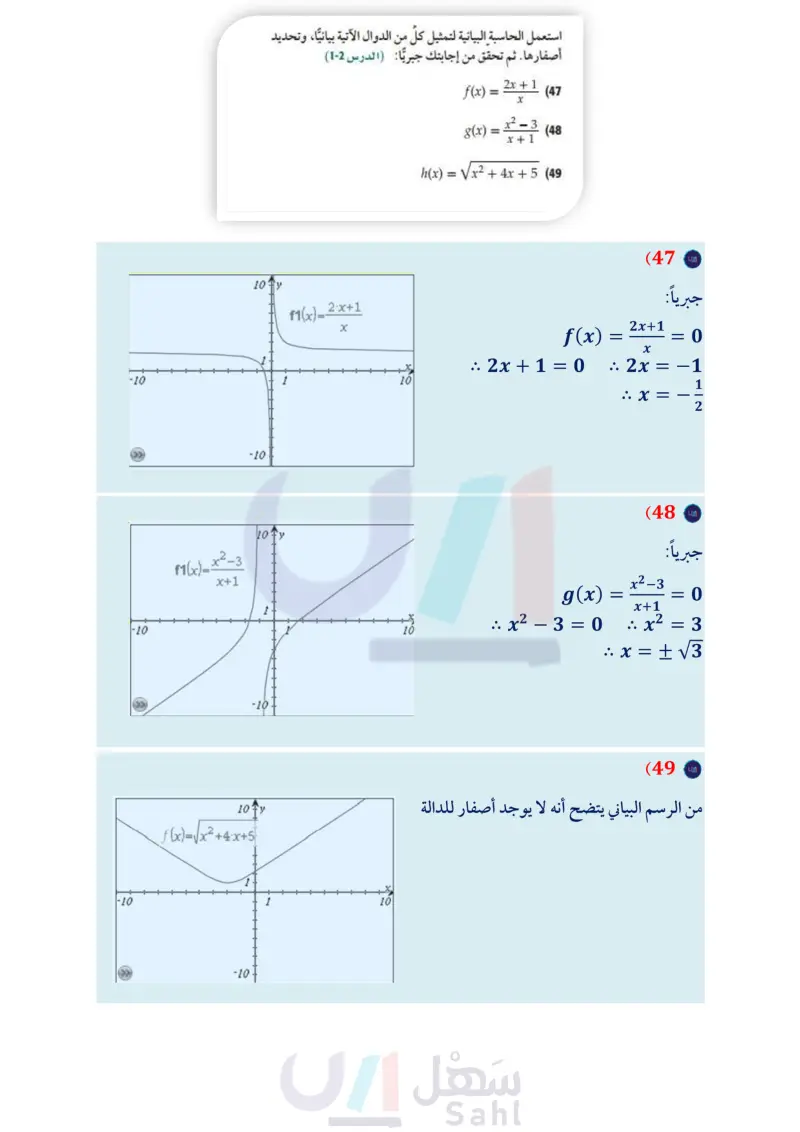
مسائل مهارات التفكير العليا إذا كانت 2x 5 x2 - 3x + 1 تبرير بين إذا كان لكل من الدالتين الآتيتين عدم اتصال لانهائي، أم قفزي، أم قابل للإزالة عند 0 = x . برر إجابتك. مما يأتي: (الدرس 1-1) f(9) (53 f(3b) (54 f(x) = x³ + x^ x5 x6 x5 (39 f(x) = x²± (40 x4 f(2a-3) (55 = = (f(x فأوجد قيمة الدالة في كل 41) تحد أوجد قيمة كل من a b التي تجعل الدالة أمتصلة. 2 X +a x≥ 3 , f(x) = bx + a -b-x -3< x <3 ' x ≤ -3 مثل بيانيا كل من الدوال الآتية باستعمال الحاسبة البيانية، ثم حلل منحناها لتحدّد إن كانت الدالة زوجية أم فردية أم غير ذلك. ثم تحقق من إجابتك جبريًا. وإن كانت زوجية أو فردية فصف تماثل منحناها (الدرس (2-1) تبرير أوجد (lim f(x في كلِّ من الحالات الآتية، وبرر إجابتك. = (42 = ― -∞ (43 811x (lim f(x حيث أدالة زوجية. (lim f(x حيث fدالة فردية. XX' (44) lim f(x) = oo حيث أدالة متماثلة حول نقطة الأصل. x-x (45) lim f(x) = oo حيث دالة متماثلة حول المحور . X X (46) اكتب: أعط مثالا على دالة لها عدم اتصال قابل للإزالة، ثم بيّن كيف يمكن إزالته. وكيف تؤثر إزالة عدم ا عدم الاتصال في الدالة؟ h(x) = √x² -9 (56 f(x) = x + 3 (57 +4 2 تدريب على اختبار 58 يبين التمثيل البياني أدناه منحنى دالة كثيرة الحدود (f(x أي الأعداد الآتية يمكن أن يكون درجة للدالة (f(x؟ X y مراجعة تراكمية استعمل الحاسبة البيانية لتمثيل كل من الدوال الآتية بيانيا، وتحديد أصفارها. ثم تحقق من إجابتك جبريًّا (الدرس (2-1) f(x) = g(x) 2x + 1 (47 X x² - 3 = (48 x + 1 h(x) = √√x² + 4x + 5 (49 حدد مجال كل من الدوال الآتية: (الدرس 1-1 f(x) = = g(x) = 4x + 6 x2 + 3x + 2 x + 3 x2 – 2x - 10 (50 (51 g (a) = V2 - a2 (52) 1 A 2 B 3C 4 D (59) في أي الفترات الآتية يقع صفر الدالة 6 - 6 - f(x) = V x2 ؟ [6,7] A [7,8] B [8,9] C [9,10] D وزارة التعليم الدرس 3-1 الاتصال والنهاياتM35 of E 2024-1446