تحليل التمثيلات البيانية للدوال والعلاقات - رياضيات1-3 - ثالث ثانوي
الفصل الأول: تحليل الدوال
الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
الفصل الثالث: المتطابقات والمعادلات المثلثية
الفصل الرابع: القطوع المخروطية
نشاط الفصل الأول: تحليل الدوال
نشاط الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
نشاط الفصل الثالث: المتطابقات والمعادلات المثلثية
نشاط الفصل الرابع: القطوع المخروطية
تحليل التمثيلات البيانية للدوال والعلاقات رابط الدرس الرقمي www.ien.edu.sa Analyzing Graphs of Functions and Relations 1-2 فيما سبق: درست الدوال وكيفية إيجاد قيمها. ( الدرس 1-1) والآن : أستعمل التمثيل البياني لتقدير قيم الدالة، وإيجاد مجالها، ومداها، لماذا ؟ تولي المملكة أهمية متزايدة للقطاع الصحي، وينعكس ذلك على الميزانية المخصصة له. فمثلا يمكن تقدير مخصصات الصحة والهلال الأحمر (بمليارات الريالات خلال الفترة من ( 1440 - 1433 ) هـ بالدالة: 15 f(x) = -0.0015x4 + 0.0145x3 + 0.3079x2 -0.5654x + 14.07 ,1≤x<8 . ومقطعها ، وأصفارها. حيث تمثل x رقم السنة منذ عام 1433هـ . ويساعدك التمثيل البياني لهذه الدالة على فهم العلاقات بين المتغيرات في - أستكشف تماثل منحنيات هذا الموقف الحياتي. الدوال، وأحدد الدوال الزوجية والدوال الفردية. المفردات: الأصفار zeros الجذور roots التماثل حول مستقيم line symmetry التماثل حول نقطة point symmetry الدالة الزوجية even function الدالة الفردية odd function تحليل التمثيل البياني للدالة : التمثيل البياني للدالة f هو مجموعة الأزواج المرتبة ((x, f(x) ، حيث x أحد عناصر مجال f. وبمعنى آخر فإن التمثيل البياني للدالة f هو منحنى المعادلة (y = f(x. ومن ثم تكون القيمة المطلقة لقيمة الدالة مساويةً طول العمود الواصل من نقطة على المحور x إلى منحنى الدالة، كما هو موضح في الشكل المجاور. يُستعمل التمثيل البياني للدالة في كثير من الأحيان لتقدير قيم الدالة. تقدير قيم الدوال مثال 1 من واقع الحياة مخصصات : استعمل التمثيل البياني المجاور للدالة f الواردة في فقرة "لماذا؟" للإجابة عما يأتي: a قدر قيمة المخصصات سنة 1438 هـ ، ثم تحقق من إجابتك جبريًا. السنة 1438 هـ هي ، السنة السادسة بعد 1432 هـ ، لذا تُقدر قيمة الدالة عند 6 = x بـ 23 مليار ريال، وعليه تكون المخصصات سنة 1438هـ هي 23 مليار ريال تقريبًا. وللتحقق من من ذلك جبرياً، أوجد قيمة (6)f بالتعويض في الدالة. x (x, f(x)) if(x) X f (1) АУ |y = f(x) مخصصات الصحة والهلال الأحمر | y= f(x) T -2 f(-2) 30 20 10 المخصصات ( بمليارات الريالات) 012 3 4 5 ما وزارة التعليم Ministry of Education 2024-1446 10 السنوات منذ 1432هـ 7 8 f(6) = -0,0015(6) 4 + 0.0145(6)³ + 0.3079(6)2-0.5654(6) + 14.07 ≈ 22.95 لذا يُعد التقريب 23 مليارًا باستعمال التمثيل البياني معقولا. قدر السنة التي كانت فيها قيمة المخصصات 15 مليار ريال، ثم تحقق من إجابتك جبريًا. يبين التمثيل البياني أن قيمة الدالة تكون 15 مليارًا عندما تكون قيمة x قريبة من العدد 3 ، لذا تكون المخصصات 15 مليارًا في سنة 1435 هـ . وللتحقق جبريًا أوجد (3)f . . f(3) = -0.0015(3) 4 + 0.0145(3) 3 + 0.3079(3)² - 0.5654(3) + 14.07≈15.4149 لذا تعد السنة التقريبية 1435هـ معقولة. الفصل 1 تحليل الدوال 16

استعمل التمثيل البياني لتقدير قيم الدالة.
تحقق من فهمك 1) استثمار: تمثل الدالة: 20 = d = 0.002d4 - 0.11d3 + 1.77d2 - 8.6d + 31, 0 ≤ d) تقديرًا لاستثمارات أحد رجال الأعمال في السوق المحلية؛ حيث ( قيمة الاستثمارات بملايين الريالات في السنة d. قيم الاستثمار قيمة الاستثمارات ( بملايين الريالات 42 36 30 24 18 12 26 0 2 4 6 8 10 12 14 16 18 20 إرشادات للدراسة اختيار التدريج المناسب : اختر تدريجًا مناسبًا لكل من المحورين x y للتمكن من رؤية منحنى الدالة بوضوح . لاحظ اختلاف التمثيل الظاهر للدالة السنوات IA) استعمل التمثيل البياني لتقدير قيمة الاستثمارات في السنة العاشرة. ثم تحقق من إجابتك جبريًا. 1B) استعمل التمثيل البياني لتحديد السنوات التي بلغت فيها قيمة الاستثمارات 30 مليون ريال. ثم تحقق من إجابتك جبريًا. لا يقتصر استعمال منحنى الدالة على تقدير قيمها، إذ من الممكن استعماله لإيجاد مجال الدالة ومداها. حيث يُعدُّ منحنى الدالة ممتدا من طرفيه إلا إذا حُدِّد بنقطة أو دائرة. مثال 2 إيجاد المجال والمدى أوجد مجال الدالة f ومداها باستعمال التمثيل البياني المجاور . المجال: تدل النقطة عند (10) على أن المجال يبدأ عند 8- = x . 3 f(x) = x 4 – 20x أدناه. • تدل الدائرة عند النقطة - على أن 4 = x ليست في مجال f . 10 19 1.1 10+y f1(x)=x-20-x3 10 • يدل السهم على الجهة اليمنى من المنحنى على استمرارية المنحنى من اليمين دون حدود (دون توقف). y -8 -4 O 4 8x y = f(x) | مما سبق يكون مجال الدالة f هو (4) 84] . وباستعمال الصفة المميزة للمجموعة يكون المجال . {x | x ≥-8, x-4, x = R} s المدى - إن أقل قيمة للدالة هي (8) أو 10 ، وتزداد قيم (f(x بلا حدود عندما تزداد قيم x ، لذا فإن مدى الدالة f هو -10 <-19-2 1.1 20000 f1(x)=x4-20 x³ 2000 . [-10, ∞) 15 تحقق من فهمك y 8 (2B y ·8· الله y = g ( x ) | y = g(x) 4 -8 4 -4 O 8x -4- -40 4 8 X =8- وزارة التعليم الدرس 2-1 تحليل التمثيلات البيانية للدوال والعلاقاتMi17y of E 2024-1446 (2A -20000

اختيار التدريج المناسب
النقطة التي يتقاطع عندها المنحنى مع المحور x أو المحور y تسمى المقطع من ذلك المحور. ويمكن الحصول على المقطع x بتعويض 0 = y في معادلة الدالة، كما يمكن الحصول على المقطع لا بالتعويض عن 0 = x في معادلة الدالة. وبشكل عام فإنه ليس من الضروري أن يكون للدالة مقطع x، وقد يكون هناك مقطع x واحد أو أكثر، وأما بالنسبة للمقطع ل فإن للدالة مقطع واحد على الأكثر. ثلاثة مقاطع من المحور X y مقطع المحور y x ولإيجاد المقطع لا لمنحنى الدالة f جبريًا، فإننا نوجد (0)f. مثال 3 إيجاد المقطع لا استعمل التمثيل البياني لكل من الدالتين أدناه، لإيجاد قيمة تقريبية للمقطع y، ثم أوجده جبريًا: y g(x)=|x-5|-1 0 x (b (a y | f(x) = -2x+4 3 x التقدير من التمثيل البياني : يتضح من الشكل أن (f(x يقطع المحور لا عند النقطة (0) تقريبا، وعليه فإن المقطع لا هو 1 تقريبا. الحل جبريًا : أوجد قيمة (0)f . التقدير من التمثيل البياني: يتضح من الشكل أن (x) يقطع المحور عند النقطة (4) ، وعليه فإن المقطع ل هو 4 الحل جبريًا : أوجد قيمة (0). g(0) = |05| − 1 = 4 - 3 4 (0) = - 2000 + 1 = 1 = 13 3 أي أن المقطع y هو 4 أي أن المقطع لا هو و أو 13. 3 تحقق من فهمك إرشادات للدراسة تدريج المحورين : إذا لم يظهر التدريج على المحورين x, y في التمثيل البياني، فذلك يعني أن التدريج بالوحدات. انظر المثال 3a 2 17 y -4-3-2-10 1 2 3 4x إرشادات للدراسة تسمية المحورين في التمثيل البياني: عندما تُسمي المحورين في التمثيل البياني، فإن المتغير الذي يدل على المجال يكون على المحور x ، والمتغير الذي يدل على المدى يكون على المحور y . ويمكن أن تستعمل متغيرات كثيرة لكل من المجال والمدى . ولكن للتسهيل نسمي عادة المحور الأفقي x والرأسي y . (3 f(x) = x3 + x2 - 6x + 4 4x lov y 12 -20 -4 2 (3B √x²+6 8 انه 4 |h(x) = -8 -40 4 8x -4 -8 تُسمى المقاطع x لمنحنى الدالة أصفار الدالة، وتُسمى حلول المعادلة المرافقة للدالة جذور المعادلة. ولإيجاد أصفار دالة ، فإننا نحل المعادلة 0 =(f (x بالنسبة للمتغير المستقل. وزارة التعليم Ministry of Education 2024-1446 الفصل 1 تحليل الدوال 18

تدريج المحورين x.y
تسمية المحورين في التمثيل البياني
-8 -40 -4 -8- YA 8x | f(x) = 2x2 + x - 15 مثال 4 إيجاد الأصفار استعمل التمثيل البياني المجاور، الذي يمثل الدالة 15 – f(x) = 2x2 + x لإيجاد قيم تقريبية لأصفارها، ثم أوجد هذه الأصفار جبريًا. التقدير من المنحنى يتضح من التمثيل البياني أن مقطعي المحور x هما 3 و 2.5 تقريبًا. لذا فإن صفري الدالة f هما 3 و 2.5 الحل جبريًّا : 2x2 + x – 15 = 0 (2x-5)(x+3)= 0 أو 2x - 5 = 0 2.5 = x أو ضع 0 = (f(x حلل 0 = 3 + x خاصية الضرب الصفري x = = -3 حل كل معادلة أي أن جذري المعادلة 0 = 15 - 2x 2 + x هما 3 و 2.5 وهما صفرا الدالة f . تحقق من فهمك (4B h(t) = V4t + 1 O x y 8 ہے -4 -20 4x | f(x) = 3x3 - 10x 2 + 8x (4A إرشادات للدراسة تماثل العلاقات والدوال يكون التماثل حول المحور x للعلاقات فقط . أما التماثل حول المحور ل ونقطة الأصل فيكون للعلاقات والدوال. التماثل: يوجد لتمثيلات العلاقات البيانية نوعان من التماثل : التماثل حول مستقيم، حيث يمكن طي الشكل على المستقيم لينطبق نصفا المنحنى تماما ، و التماثل حول نقطة أي إذا تم تدوير الشكل بزاوية قياسها °180 حول النقطة فإنه لا يتغير. وفيما يأتي تلخيص لأهم أنواع التماثل : مفهوم أساسي اختبارات التماثل اختبار التمثيل البياني يكون تمثيل العلاقة البياني متماثلا حول المحور x ، إذا وفقط إذا تحقق الشرط التالي: إذا كانت النقطة (x,y) واقعة على التمثيل البياني، فإن النقطة (x,y) تقع عليه أيضًا. يكون تمثيل العلاقة البياني متماثلاً حول المحور y ، إذا وفقط إذا تحقق الشرط التالي : إذا كانت النقطة (x,y) واقعة على التمثيل البياني ، فإن النقطة (x,y) تقع عليه أيضًا. يكون تمثيل العلاقة البياني متماثلا حول نقطة الأصل ، إذا وفقط إذا تحقق الشرط التالي: إذا كانت النقطة (x,y) واقعة على التمثيل البياني، فإن النقطة x -y-( تقع عليه أيضًا. X x xX (x,y) النموذج y (x, y) (x, (-x, y) (x, y) (−x, −y) الاختبار الجبري إذا كان تعويض - مكان ل يعطي معادلة مكافئة . - إذا كان تعويض x مكان x يعطي معادلة مكافئة إذا كان تعويض x- مكان x و - مكان لا يعطي معادلة مكافئة. وزارة التعليم الدرس 2 -1 تحليل التمثيلات البيانية للدوال والعلاقاتMi19 of E 2024-1446

تماثل العلاقات والدوال
إرشادات للدراسة التماثل : مثال 5 اختبار التماثل من الممكن أن يكون للتمثيل استعمل التمثيل البياني لكل من المعادلتين الآتيتين لاختبار التماثل حول المحور x والمحور y ونقطة الأصل. عزّز إجابتك عدديًا، ثم تحقق منها جبريًا. البياني الواحد أكثر من نوع تماثل. y -8 |x − y² = 1 4- 10 -4- -8- 8 12 x . x - y2 = 1 (a التحليل بيانيا : يتضح من التمثيل البياني أن المنحنى متماثل حول المحور x ؛ لأنه لكل نقطة (x,y) على المنحنى، فإن النقطة (x,y) تقع أيضًا على المنحنى. التعزيز عدديًا : يبين الجدول أدناه وجود تماثل حول المحور x : x 2 2 5 5 10 10 y 1 −1 2 -2 3 -3 (x, y) (2, 1) (5, 2) (2,-1) (5,-2) (10, 3) (10,-3) التحقق جبريًا : بما أن المعادلة 1 = 2(x - (y تكافئ 1 = 2 - x ، فإن المنحنى متماثل حول المحور x 8 xy=4 4 410 4 8x وزارة التعليم Ministry of Education 2024-1446 xy=4 (b التحليل بيانيا : يتضح من التمثيل البياني أن المنحنى متماثل حول نقطة الأصل؛ لأنه لكل نقطة على المنحنى، فإن النقطة (x,y) تقع أيضًا على المنحنى. التعزيز عدديًا : يبين الجدول الآتي وجود تماثل حول نقطة الأصل: X -8 y -0.5 (x, y) (-8, -0.5) -2 -2 (-2,-2) -0.5 0.5 2 8 -8 8 2 0.5 (-0.5, -8) (0.5, 8) (2,2) (8, 0.5) التحقق جبريًا : بما أن المعادلة 4 - (x) (y) تكافئ 4 = xy، فإن المنحنى متماثل حول نقطة الأصل. تحقق من فهمك = (5B บ 8 00 x2 + y2 = 25 4 -8 -4 O 4 8x -4 -8 y = - x2 + 6 -8 -4 4 8x -4- -8- (5A الفصل 1 تحليل الدوال 20

التماثل
يمكن أن تتماثل منحنيات الدوال حول المحور y فقط أو حول نقطة الأصل فقط؛ ولهذين النوعين من الدوال اسمان خاصان الدوال الزوجية والدوال الفردية مفهوم أساسي نوع الدالة الاختبار الجبري تُسمى الدوال المتماثلة حول المحور y الدوال الزوجية. لكل x في مجال ،f ، فإن (f(x) = f(x . تُسمى الدوال المتماثلة حول نقطة الأصل الدوال الفردية. لكل x في مجال ، ، فإن (f(x) = - f(x . مثال 6 تحديد الدوال الزوجية والدوال الفردية استعمل الحاسبة البيانية لتمثل كل دالة مما يأتي بيانيًا . ثمَّ حلّل منحناها لتحدّد إن كانت الدالة زوجية أم فردية أم غير ذلك. ثم تحقق من إجابتك جبريًا. f(x) = x3 - 2x a يتضح من التمثيل البياني أن الدالة متماثلة حول نقطة الأصل، لذا فهي دالة فردية، وللتحقق من ذلك جبريًّا نجد (f(x) = (x)3 - (x عوض x مكان X 23-1 1.1 f1(x)=x³-2x 0.5 -5 f1(x)=x+2 5 0.5 23-2 1.1 -23-3 1.1 | f(x)=x3-0.5x2-3.x 0.5 -5 بسط خاصية التوزيع الدالة الأصلية f(x) = x3 - 2x = -x3 + 2x = -(x³-2x) = - f(x) أي أن الدالة فردية؛ لأن (f(x) = f(x . f(x) = x4 + 2 (b يتضح من التمثيل البياني أن الدالة متماثلة حول المحور y، لذا فهي دالة زوجية، وللتحقق من ذلك جبريًّا نجد 2 + 4(f(x) = (x عوض x مكان x = 2 + x4 = بسط = f(x) الدالة الأصلية 2 + 4 f(x) = x أي أن الدالة زوجية؛ لأن (f(x) = f(x. f(x) = x³- 0.5 x² - 3x (c X يتضح من التمثيل البياني أن الدالة ليست متماثلة حول المحور y وليست متماثلة حول نقطة الأصل، وللتحقق من ذلك جبرياً نجد f(x) = (-x)³ − 0.5(-x)² - 3(-x) = - 3 - 0.5x2 + 3x عوض x- مكان x بسط وبما أن f(x) = x3 + 0.5x2 + 3x - ، 6 فإن (f(x) f(x ، وكذلك (f(x) ( - f(x لذا فالدالة ليست زوجية وليست فردية. - h(x) = x5 = 2x³ +x (6C g(x) = 4√√x (6B وزارة التعليم الدرس 2-1 تحليل التمثيلات البيانية للدوال والعلاقات21y of E 2024-1446 تحقق من فهمك f(x) = 22 (6A x2 إرشادات للدراسة الدوال الزوجية والدوال الفردية : قد تظهر لك بعض التمثيلات البيانية تماثلًا والحقيقة غير ذلك؛ لذا عليك التأكد من التماثل جبريًا في كل مرة.

الدوال الزوجية والدوال الفردية
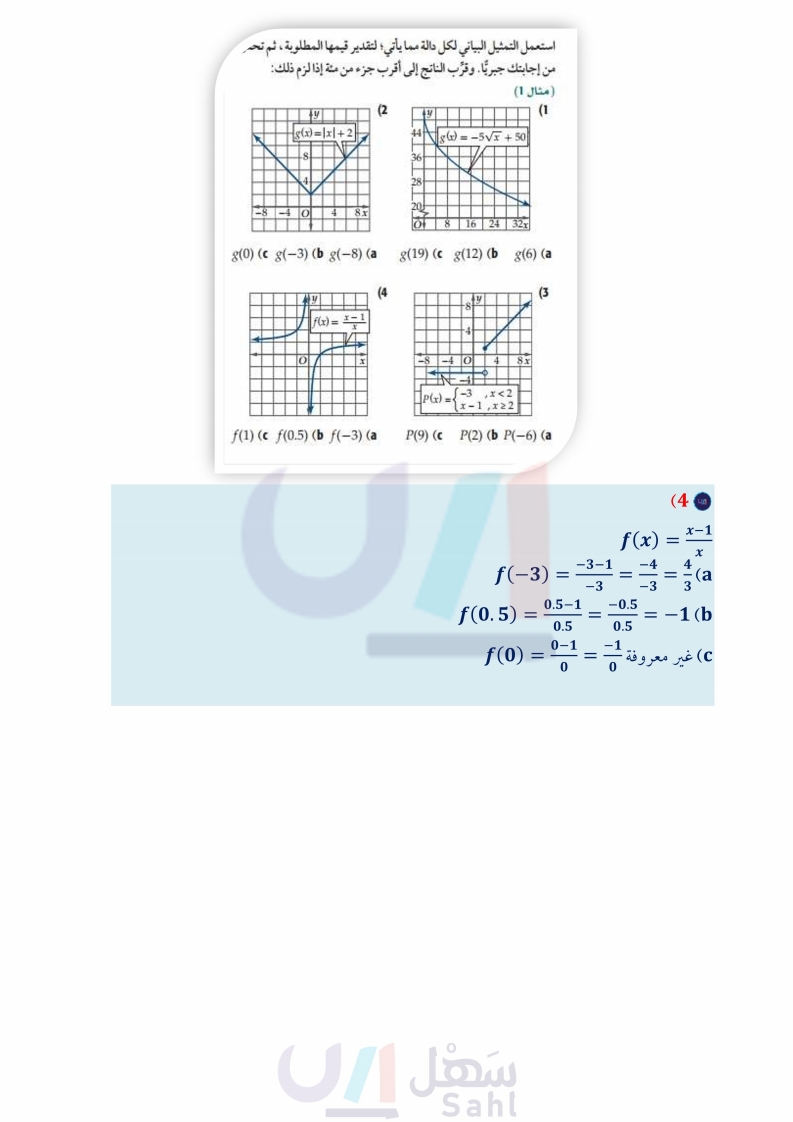
تدرب وحل المسائل استعمل التمثيل البياني لكل دالة مما يأتي؛ لتقدير قيمها المطلوبة ، ثم تحقق استعمل التمثيل البياني للدالة في كل مما يأتي لإيجاد كل من مجال من إجابتك جبريًا. وقرب الناتج إلى أقرب جزء من مئة إذا لزم ذلك: الدالة ومداها (مثال (2) y = h(x) y (7 y y = h(x) x X (9 y y=h(x) X (6 (مثال 1) (2 y y (1 |g(x)=|x|+2 44 g(x) = -5√√x +50 8. 36 4 28 20 -8-40 4 8x f 24 16 32x 19 h(x) (8 g(0) (c g(-3) (b g(−8) (a g(19) (c g(12) (b g(6) (a X (4 y | f(x) = x = 1 - X + (3 y x -8 -4 O 4 8x -4 -3 P(x) X- ,x<2 1,x≥2 10 f(1) (c f(0.5) (b ƒ(−3) (a P(9) (c P(2) (b P(-6) (a (5) مياه : إذا كانت كمية المياه المحلاة في محطة الخبر (بملايين المترات المكعبة) في الفترة ( 1431هـ إلى 1437هـ ) معطاة بالدالة (10) هندسة : أُجريت اختبارات على الخصائص الفيزيائية لعينات من أربع قطع معدنية، حيث أخضعت لدرجات حرارة سيليزية مختلفة. فإذا كانت الطاقة المخزنة أو الممتصة في العينة خلال الاختبار مقاسة بالجول (J) كما هو موضح في الشكل أدناه، فأجب عما يأتي: ( مثال 2 ) نتائج اختبار خصائص المواد الطاقة المخزنة ( 1 ) 2.5 2.0 1.5 1.0 نحاس. الومنيوم زنك 0.5 فولاذ 0.0 -150-100 -50 0 50 100 150 الحرارة ( C ) a أوجد المجال والمدى لكل دالة. استعمل التمثيل البياني لتقدير الطاقة المخزنة في كل معدن عند الصفر السيليزي. استعمل التمثيل البياني لكل دالة مما يأتي؛ لإيجاد مقطع المحور y ، وأصفار الدالة، ثم أوجد أصفار الدالة جبريًّا ( المثالان (34) وزارة التعليم Ministry of Education 2024-1446 YA (12 y x | f(x) = Vx - 1 f(x) = 2x3 - x2 - 3x ΟΙ 18 (11 f(x) = 0.0509x4 - 0.3395x3 - 2.28x2 + 25.35x + 88.27 حيث تمثل x رقم السنة منذ عام 1430هـ . ( مثال (1) كمية المياه المحلاة في محطة الخبر الكمية ) بملايين المترات المكعبة ) 150 100 50 50 0 1 2 3 4 5 6 7 8 السنوات منذ 1430 هـ قدر كمية المياه المحلاة في سنة 1435 هـ باستعمال التمثيل البياني. أوجد كمية المياه المحلاة في سنة 1435 هـ جبريًا مقربًا إجابتك إلى أقرب جزء من عشرة. قدّر السنة التي كانت كمية المياه المحلاة فيها 130 مليون متر مکعب باستعمال التمثيل البياني، وتحقق من إجابتك جبريًّا. الفصل 1 تحليل الدوال 22

استعمل التمثيل البياني لكل دالة مما يأتي لتقدير قيمها المطلوبة ثم تحقق من إجابتك جبريا وقرب الناتج إلى أقرب جزء من مئة إذا لزم ذلك


تدرب وحل المسائل استعمل التمثيل البياني لكل دالة مما يأتي؛ لتقدير قيمها المطلوبة ، ثم تحقق استعمل التمثيل البياني للدالة في كل مما يأتي لإيجاد كل من مجال من إجابتك جبريًا. وقرب الناتج إلى أقرب جزء من مئة إذا لزم ذلك: الدالة ومداها (مثال (2) y = h(x) y (7 y y = h(x) x X (9 y y=h(x) X (6 (مثال 1) (2 y y (1 |g(x)=|x|+2 44 g(x) = -5√√x +50 8. 36 4 28 20 -8-40 4 8x f 24 16 32x 19 h(x) (8 g(0) (c g(-3) (b g(−8) (a g(19) (c g(12) (b g(6) (a X (4 y | f(x) = x = 1 - X + (3 y x -8 -4 O 4 8x -4 -3 P(x) X- ,x<2 1,x≥2 10 f(1) (c f(0.5) (b ƒ(−3) (a P(9) (c P(2) (b P(-6) (a (5) مياه : إذا كانت كمية المياه المحلاة في محطة الخبر (بملايين المترات المكعبة) في الفترة ( 1431هـ إلى 1437هـ ) معطاة بالدالة (10) هندسة : أُجريت اختبارات على الخصائص الفيزيائية لعينات من أربع قطع معدنية، حيث أخضعت لدرجات حرارة سيليزية مختلفة. فإذا كانت الطاقة المخزنة أو الممتصة في العينة خلال الاختبار مقاسة بالجول (J) كما هو موضح في الشكل أدناه، فأجب عما يأتي: ( مثال 2 ) نتائج اختبار خصائص المواد الطاقة المخزنة ( 1 ) 2.5 2.0 1.5 1.0 نحاس. الومنيوم زنك 0.5 فولاذ 0.0 -150-100 -50 0 50 100 150 الحرارة ( C ) a أوجد المجال والمدى لكل دالة. استعمل التمثيل البياني لتقدير الطاقة المخزنة في كل معدن عند الصفر السيليزي. استعمل التمثيل البياني لكل دالة مما يأتي؛ لإيجاد مقطع المحور y ، وأصفار الدالة، ثم أوجد أصفار الدالة جبريًّا ( المثالان (34) وزارة التعليم Ministry of Education 2024-1446 YA (12 y x | f(x) = Vx - 1 f(x) = 2x3 - x2 - 3x ΟΙ 18 (11 f(x) = 0.0509x4 - 0.3395x3 - 2.28x2 + 25.35x + 88.27 حيث تمثل x رقم السنة منذ عام 1430هـ . ( مثال (1) كمية المياه المحلاة في محطة الخبر الكمية ) بملايين المترات المكعبة ) 150 100 50 50 0 1 2 3 4 5 6 7 8 السنوات منذ 1430 هـ قدر كمية المياه المحلاة في سنة 1435 هـ باستعمال التمثيل البياني. أوجد كمية المياه المحلاة في سنة 1435 هـ جبريًا مقربًا إجابتك إلى أقرب جزء من عشرة. قدّر السنة التي كانت كمية المياه المحلاة فيها 130 مليون متر مکعب باستعمال التمثيل البياني، وتحقق من إجابتك جبريًّا. الفصل 1 تحليل الدوال 22

(33) دوال : إذا كانت "f(x) = x ، حيث n e N فأجب عن الأسئلة الآتية: (42) أسهم: افترض أن النسبة المئوية للتغير في سعر سهم خلال سنة a استعمل الحاسبة البيانية لتمثل (f(x بيانيا لكل قيمة من قيم n في الفترة 6 = n > 1 . اكتب المجال والمدى لكل دالة. صف التماثل لكل دالة. تنبأ بمجال الدالة 35 f ( x ) = x، ومداها، وتماثلها، ثم برّر إجابتك. (34) صيدلة : إذا كان عدد ملجرامات الدواء في دم مريض بعد x ساعة من تناوله الدواء يعطى بالدالة : f(x) = 0.5x4 + 3.45x3 - 96.65x2 + 347.7x a استعمل الحاسبة البيانية لتمثل الدالة بيانيا اكتب المجال المناسب للدالة، وفسّر إجابتك. ما أكبر عدد من ملجرامات الدواء يكون موجودًا في دم المريض وفق هذه الدالة؟ الحاسبة البيانية مثل كلَّا من الدوال الآتية بيانيا، وحدّد أصفارها، ثم تحقق من أصفار الدالة جبريا: f(x) : 4x - 1 = (35 x f(x) = x2 + 9 x + 3 4 (36 8(x) = −12+ (38 h(x) = 2Vx + 12 - 8 (37 استعمل التمثيل البياني للدالة f لتحدد مجالها ومداها في كل مما يأتي: (39 8 -f(x)=- -4 واحدة تعطى بالدالة : p(x) = 0.0005x4 — 0.0193x³ + 0.243x² – 1.014x + 1.04 حيث x رقم الشهر بدءًا من شهر يناير. استعمل الحاسبة البيانية لتمثل الدالة بيانيًا. أوجد مجال الدالة، ثم قدّر مداها. استعمل المنحنى لتقريب قيمة المقطع ، وماذا يمثل؟ أوجد أصفار الدالة، ووضّح معناها. 1 x-2 (543 تمثيلات متعددة : سوف تستقصي في هذه المسألة مدى قيم الدالة 2 = (f(x عندما تقترب x من العدد 2. a جدوليًا : انقل الجدول الآتي إلى دفترك. وأضف قيما أخرى للمتغير x إلى يمين العدد 2 وإلى يساره. ثم أكمل الجدول. X 1.99 1.999 2 2.001 2.01 f(x) b تحليليا : معتمدًا على جدولك، ما القيمة أو القيم التي تقترب منها الدالة عندما تقترب x من العدد 2؟ بيانيا : مثل الدالة بيانيًا . وهل يؤكد التمثيل البياني تخمينك في الفرع ؟ وضح إجابتك . d لفظيا خمّن القيمة التي تقترب منها الدالة من خلال التمثيل البياني في الفرع ، ووضح إجابتك . . الحاسبة البيانية : مثَّل كلَّا من الدوال الآتية بيانيا، ثم حلل منحناها لتحدد ما إذا كانت الدالة زوجية أم فردية أم غير ذلك. f(x) = x² − x − 6 (45 h(x) = x5 - 17x³ + 16x (44 f(g) = g³ (47 f(z) = 23 - 422 + 42 (49 h(x) = x6 + 4 (46) g(x) = x4 + 8x2 + 81 (48 -8 -49 4 8 80 X y (40 8 4 √f(x)= -4 O 4 8 x -4- (41) فيزياء : إذا كان مسار أحد المذنبات حول الشمس يُعطى بالعلاقة: x2 12 = + 1 8 10 a صف تماثل منحنى مسار المذنب. b استعمل التماثل لتمثيل منحنى العلاقة. إذا مر المذنب بالنقطة (V5 (2) ، فعيّن ثلاث نقاط أخرى يجب أن يمر بها المذنب. مسائل مهارات التفكير العليا مسألة مفتوحة : مَثَّل بيانيًا منحنى يحقق الشروط في كل حالة مما يأتي: 6 (50) منحنى يمر بالنقاط 1 ,8-) ,(2 ,5 ,4 ,4) ,(38) ، و متماثل حول المحور y . 51) منحنى يمر بالنقاط 4,4) ,(12 ,3) ,(6 ,2) ,0 ,0) ، ومتماثل حول المحور x . (52) منحنى يمر بالنقاط -3- ,1-) ,(9- ,2-) ,(318) ، ومتماثل حول نقطة الأصل. (53) منحنى يمر بالنقاط (88) ,(612) ,(416) ويمثل دالة زوجية. (54) اكتب وضح لماذا يمكن أن يكون للدالة 0 أو 1 أو أكثر من مقاطع x ، بينما يوجد لها مقطع y واحد على الأكثر. وزارة التعليم Ministry of Education 2024-1446 الفصل 1 تحليل الدوال 24

p(x) 2x3 + 2 = (70 x2 2 p(3) (a P(x2) (b p(x + 1) (c h(x) =2x2 + 4x - 7 (71) h(-9) (a h(3x) (b h(2m) (c أوجد مجال كل دالة من الدوال الآتية (الدرس 1-1) 5 f(x) = x2 - V2 (12) f(x) : = 2 1 X - 16 - (73 f(x) = V3x + 18 (74 بسط كلًا مما يأتي: (مهارة سابقة) 646 (76 3 16-1 16 4 (78 36 - 3 36 2 (80 27 1/3 273 (75 49 - 11/1 49 2 (77 3 252 (79 (55) تحد: أوجد مجال الدالة 2 - 2x2 + 3x x3 – 4x2 – 12x برّر إجابتك ، ثم تحقق منها بيانياً. = : (f(x ، ومداها. تبرير أي العبارات الآتية صحيحة، وأيها خاطئة. برر إجابتك. (56 مدى الدالة f(x) = nx2 ، حيث 11 عدد صحيح، هو {y | y ≥ 0, y = R} (57) مدى الدالة f(x) = Vnx ، حيث 11 عدد صحيح، هو {y | y ≥ 0, y = R} جميع الدوال الفردية متماثلة حول المستقيم y = x . (58 (59) إذا دارت دالة زوجية n180 حول نقطة الأصل، حيث 1 عدد صحیح، فإنها تبقى زوجية. تبرير: إذا كانت (a(x دالة فردية، فحدد ما إذا كانت الدالة (x) فردية، أم زوجية، أم غير ذلك في كل مما يأتي، وبرر إجابتك: b(x) = a(-x) (60 b(x) = a(x) (61 b(x) = [a(x)]2 (62) b(x) = a(|x|) (63 b(x) = [a(x)]³ (64 تدريب على اختبار معياري ئمًا أم تبرير هل يمثل المنحنى المعطى تماثله في كل مما يأتي دالة دائمًا أحيانًا أم لا يمثل دالة؟ وبرر إجابتك. (65) متماثل حول المستقيم 4 = x . (66) متماثل حول المستقيم 2 = y . (81) إذا كان n عددًا حقيقيًا أكبر من ،1 فأوجد قيمة x بدلالة n في الشكل أدناه. √n Vn + 1 C X V2 - 1 A Vn - 1 B (67) متماثل حول كل من المحورين xy (68 اكتب وضح لماذا لا تكون العلاقة المتماثلة حول المحورx دالة. مراجعة تراكمية أوجد القيم المطلوبة لكل دالة مما يأتي : ( الدرس (1-1) n 1 D (82) ما مدى الدالة 1 + 2 f(x) = x ، إذا كان مجالها 3 > x > 2 ؟ 1 < f(x) < 9 C 1 < f(x) < 10 D 5 < f(x) < 9 A 5 < f(x) < 10 B وزارة التعليم الدرس 2-1 تحليل التمثيلات البيانية للدوال والعلاقات M250E 2024-1446 g(x) = x² - 10x + 3 (69 g(2) (a g(-4x) (b g(13n) (c




 0
0