اللوغاريتمات والدوال اللوغاريتمية - رياضيات1-3 - ثالث ثانوي
الفصل الأول: تحليل الدوال
الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
نشاط الفصل الأول: تحليل الدوال
نشاط الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
اللوغاريتمات والدوال اللوغاريتمية رابط الدرس الرقمي www.ien.edu.sa Logarithms and Logarithmic Functions 2-3 فيما سبق: لدالة. (الدرس 7-1) والآن : لماذا؟ درست إيجاد الدالة العكسية يُرجح كثير من العلماء أن سبب انقراض سلالة الديناصورات هو النيازك التي ضربت الأرض. ويستعمل الفلكيون مقياس باليرمو (Palermo) لتصنيف أجسام الفضاء كالنيازك وغيرها اعتمادًا على مدى تأثيرها في كوكب الأرض. ولجعل المقارنة بين هذه الأجسام أكثر سهولة تم تطوير المقياس باستعمال اللوغاريتمات ، إذ يمكن إيجاد قيمة مقياس باليرمو PS لجسم فضائي من خلال الدالة R = 10PS ، حيث R الخطر النسبي الذي يسببه ذلك الجسم، ويمكن كتابة هذه الدالة بصيغة أخرى تسمى الدالة اللوغاريتمية. أجد قيمة عبارات لوغاريتمية. أمثل دوال لوغاريتمية بيانيا. المفردات: اللوغاريتم logarithm الدالة اللوغاريتمية الدوال والعبارات اللوغاريتمية: يمكنك تمثيل الدالة العكسية للدالة الأسية 2 = (f(x بيانيا من خلال تبديل قيم x و y للأزواج المرتبة التي تمثل الدالة. y y = 2x (2, 4) y=x (0, 1) (4,2) x = 2y (1, 0) x تقترب قيم x من الصفر مع تناقص قيم لا x = 29 y = 2* x y x y 1814 12 -3 -3 -2 -2 - -1 -1 1 0 1814 12 0 1 2 1 1 2 4 2 2 4 8 3 80 3 logarithmic function إرشادات للدراسة تسمى logx = y الصورة اللوغاريتمية وتسمى b = x الصورة الأسية المكافئة لها. : 20 يظهر من الجدول والتمثيل البياني أعلاه أن الدالة العكسية للدالة y = 2x هي = x . وبصورة عامة، فإن الدالة العكسية للدالة y = bx هي x = by . يسمى المتغير y في المعادلة x = by لوغاريتم x ، ويكتب عادة على الصورة y = logx ، ويقرأ لا تساوي لوغاريتم x للأساس b . مفهوم أساسي اللوغاريتم للأساس 6 التعبير اللفظي : إذا كان x عددين موجبين، حيث 1 b، يرمز للوغاريتم x للأساس 6 بالرمز logx، ويُعرف على أنه الأس لا الذي يجعل المعادلة by = x صحيحة. الرموز افترض أن 1 0 6 فإن : لكل 0 < x يوجد عدد y بحيث x = y 108 إذا وفقط إذا كان by = x 1 1 1083 27 = y ++ 39 = 27 وزارة التعليم الدرس 3-2 اللوغاريتمات والدوال اللوغاريتمية 950f 2024-1446 مثال :

تسمى log x=y الصورة اللوغاريتيمية .
أجد قيمة عبارات لوغاريتيمية.
وزارة التعليم Ministry of Education 2024-1446 يمكنك استعمال تعريف اللوغاريتمات لكتابة المعادلات اللوغاريتمية على الصورة الأسية مثال 1 . التحويل من الصورة اللوغاريتمية إلى الصورة الأسية اكتب كل معادلة لوغاريتمية مما يأتي على الصورة الأسية: 1 log4 = 4 (b 256 1 1 = = 256 1084256 log3 729 = 6 (1B = log₂ 8 = 3 (a log2 8 3 8 = 23 تحقق من فهمك 1084 16 = 2 (1A log4 يمكن استعمال تعريف اللوغاريتمات أيضًا لكتابة المعادلات الأسية على الصورة اللوغاريتمية. مثال 2 التحويل من الصورة الأسية إلى الصورة اللوغاريتمية اكتب كل معادلة أسية مما يأتي على الصورة اللوغاريتمية: 4² = 2 (b -2 42 4² = 2 → log4 2 = 12 = 1253 5 (2B 153 = 3375 (a 153 = 3375 → 108153375 = 3 ٧ تحقق من فهمك 43 = 64 (2A يمكنك استعمال تعريف اللوغاريتم لإيجاد قيمة عبارة لوغاريتمية. مثال 3 إيجاد قيمة عبارة لوغاريتمية 108749 (b 1 = 10749 بفرض أن العبارة اللوغاريتمة تساوي ل تعريف اللوغاريتم 1 49 = دون استعمال الآلة الحاسبة، أوجد قيمة كل مما يأتي: 10816 4 (a y = 4 10816 بفرض أن العبارة اللوغاريتمة تساوي y 1 - 7y 49 تعريف اللوغاريتم 4 = 169 7-2 7-2 = 74 16 = 42 41 = 42y 108749 خاصية المساواة للدوال الأسية اقسم كلا الطرفين على 2 لذا فإن 2 = -2=y 1 1 = 2y 1 2 } = y خاصية المساواة للدوال الأسية log1 256 (3B لذا فإن = = 4 10816. تحقق من فهمك log3 81 (3A تنبيه أساس اللوغاريتم قد يختلط عليك معرفة أي الأعداد هو الأساس وأيها الأس في المعادلات اللوغاريتمية؛ لذا استعمل لونين مختلفين لكتابة كل منهما في أثناء الحل؛ لمساعدتك على تنظيم حساباتك. الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 96

اساس اللوغاريتم
إرشادات للدراسة الأس الصفري . تذكر أنه لأي 60 فإن • .b0: =1 1080 غير معرف لأن الخصائص الأساسية للوغاريتمات من تعريف الدوال الأسية واللوغاريتمات يمكنك استنتاج بعض الخصائص الأساسية للوغاريتمات. مفهوم أساسي الخصائص الأساسية للوغاريتمات إذا كان 0 < ، 1 x ، b عدد حقيقي ، فإن الخصائص الآتية صحيحة: الخاصية التبرير 60 = 1 0 bx لأي قيمة لـ x . log, 1 = 0 log, b = 1 log₁ bx = x blogfx = x, x>0 b1 = b bx = bx log₁x=log₁x مثال 4 استعمال الخصائص الأساسية للوغاريتمات دون استعمال الآلة الحاسبة، أوجد قيمة كل مما يأتي إن أمكن: 1210812 4.7 (c log5 125 (a blogb x = x 12108124.7 = 4.7 53 = 125 log₁ bx = x 1085 125 = 10g5 53 log5 = 3 log10(-5) (d log 10 0.001 (b 0.001 = 103 10810 0.001 = 10g10 10 -3 = −3 تحقق من فهمك log, 81 (4A logb bx = x بما أن f(x) = 10g x معرَّف فقط عندما 0 < x ، فإن (5) 10810 غير معرَّف في مجموعة الأعداد الحقيقية. 310831 (4B تمثيل الدوال اللوغاريتمية بيانيًّا : تُسمى الدالة f(x) = 10g x ، حيث 1 ، وكل من العددين x b موجبًا b دالة لوغاريتمية. والتمثيل البياني للدالة f(x) = log x هو التمثيل البياني للدالة الرئيسة (الأم) للدوال اللوغاريتمية. مفهوم أساسي الدالة الرئيسة (الأم) للدوال اللوغاريتمية الدالة الرئيسة (الأم) : 1<f(x) = logyx, b الدالة الرئيسة (الأم) : 1>f(x) = logy x, 0 < b متصل، متباين، متناقص خصائص منحنى الدالة: متصل متباين متزايد خصائص منحنى المجال : المدى : خط التقارب : مقطع المحور x : x f(x) = Logx الدالة : مجموعة الأعداد الحقيقية المجال: الموجبة (R) مجموعة الأعداد المدى : الحقيقية (R) المحور خط التقارب : مجموعة الأعداد الحقيقية الموجبة (R) مجموعة الأعداد الحقيقية (R) المحور 1 مقطع المحور x : f(x) 1 f(x) (b, 1) (1, 0) X 0(1, 0) |f(x) = Logx| (1) -1) (b. 1) وزارة التعليم الدرس 3-2 اللوغاريتمات والدوال اللوغاريتمية of E 97 2024-1446

تمثيل الدوال اللوغاريتمية بيانيا
الاس الصفري
f(x) y = log5x (5, 1) (1, 0) x 5' مثال 5 تمثيل الدوال اللوغاريتمية بيانيًا مثل كل دالة مما يأتي بيانيا : f(x) = log5x (a الخطوة 1: حدّد الأساس. b=5 الخطوة 2 حدد نقاطا على التمثيل البياني . : بما أن 1 < 5، فاستعمل النقاط (-1), (1, 0), (b. 1) •·(³½³, −1), (1, 0), (5, 1) blāj çi أي النقاط الخطوة 3 : مثل النقاط على المستوى الإحداثي. ثم ارسم المنحنى، ولاحظ أنه متصل ومتزايد، إذ تتزايد (f(x من 0 إلى ما لا نهاية. f(x) y = log₁x 3 0 (1, 0) (3,-1) x LO +3 -4- -2- f(x) f(x) = log1 x (b 3 1 الخطوة 1: 3 = b الخطوة 2: 1 > > 0 3 (3131, 1), (1, 0), (3, −1) blä Jaziul | f(x) = log 1x (5B الخطوة 3 ارسم المنحنى. C تحقق من فهمك f(x) = log2 x (5A إرشادات للدراسة سلوك طرفي التمثيل البياني لاحظ في المثال 6a أنه مع اقتراب x من موجب مالانهاية فإن (f(x تقترب إلى موجب مالانهاية أيضًا. وتماما كما في الدوال الأسية، فإنه يمكنك تطبيق التحويلات لتمثيل الدوال اللوغاريتمية بيانيا. مثال 6 تمثيل الدوال اللوغاريتمية بيانيًا مثل كل دالة مما يأتي بيانيا : f(x) = 3 log10 x +1 (a حدد نقاط التمثيل البياني للدالة الأم y = 10810 x. بما أن 101 |f(x)=3log x+1 10 |y=log x 10 (10, 1) blöð şi ‹(½½‚ −1), (1,0), (b, 1) blä Jaziulä 1 −1), (1,0) 10 ) والتمثيل البياني للدالة المعطاة هو تحويل للتمثيل البياني للدالة f(x) = 10g10 x • 3 = a : يتسع التمثيل البياني رأسيًا. • 0 = h : لا يوجد انسحاب أفقي. • 1 = k : يسحب التمثيل البياني وحدة واحدة إلى أعلى. 1 2 3 4 5 6 7 8 9 10 x وزارة التعليم Ministry of Education 2024-1446 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 98

سلوك طرفي التمثيل البياني
f(x) = { log1 (x – 3) (b 1081 4 التمثيل البياني للدالة المعطاة هو تحويل للتمثيل البياني للدالة . f(x) = log₁ x 4 . = a : يضيق التمثيل البياني رأسيًّا. • 3 = h : يسحب التمثيل البياني 3 وحدات إلى اليمين. 0 = k : لا يوجد انسحاب رأسي. تحقق من فهمك 4/ f(x) + 321 3 -2- f(x) = { 1081 (x-3) X 0 34 -2- -3 234 y = logy x 4 f(x) = 1½ log₁ (x + 1) −5 (6B f(x) = 2 log3 (x — 2) (6A 3 الربط مع الحياة أقوى هزة أرضية في القرن العشرين ضربت شيلي عام 1960م، وبلغت قوتها 9.2 درجات على مقياس ريختر، ودمرت قرى كاملة، وقتلت آلاف السكان. مثال 7 من واقع الحياة إيجاد الدوال العكسية للدوال الأسية هزات أرضية : يقيس مقياس ريختر شدة الهزة الأرضية، وتعادل شدة الهزة الأرضية عند أي درجة 10 أمثال شدة الهزة الأرضية للدرجة التي تسبقها؛ أي أن شدة هزة أرضية سجلت 7 درجات على مقياس ريختر تعادل 10 أمثال شدة هزة أرضية سجلت 6 درجات على المقياس نفسه. ويمكن تمثيل شدة الهزة الأرضية بالدالة 1 – × 10 = y ، حيث x الدرجة على مقياس ريختر. استعمل المعلومات المعطاة في فقرة " الربط مع الحياة " لمعرفة شدة أقوى هزة أرضية في القرن العشرين. y = 10x - 1 = 109.2-1 = 108.2 = 158489319.2 الدالة الأصلية عوض 9.2 بدلاً من x بسط استعمل الحاسبة أوجد الدالة العكسية للدالة 1- 10 = y ، واكتبها على الصورة : y = 10g10 x + c . بما أن الدالة 1 y = 10 x متباينة، فإن لها دالة عكسية. y = 10x – 1 x = 10y-1 y − 1 = log10 x y = log10 x + 1 تحقق من فهمك المعادلة الأصلية بدل بين x و y وحل بالنسبة لـ y تعريف اللوغاريتمات أضف العدد 1 لكلا الطرفين (7 أوجد الدالة العكسية للدالة *0.5 = y. وزارة التعليم الدرس 3-2 اللوغاريتمات والدوال اللوغاريتمية 990 2024-1446

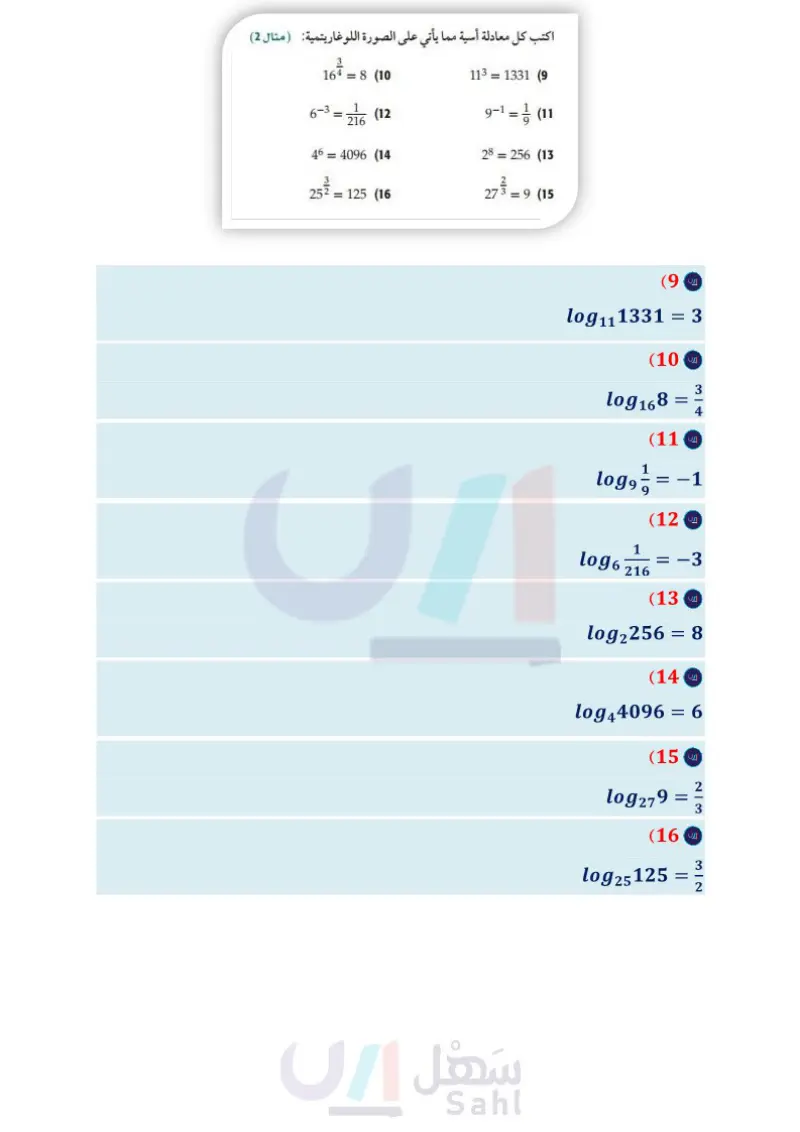
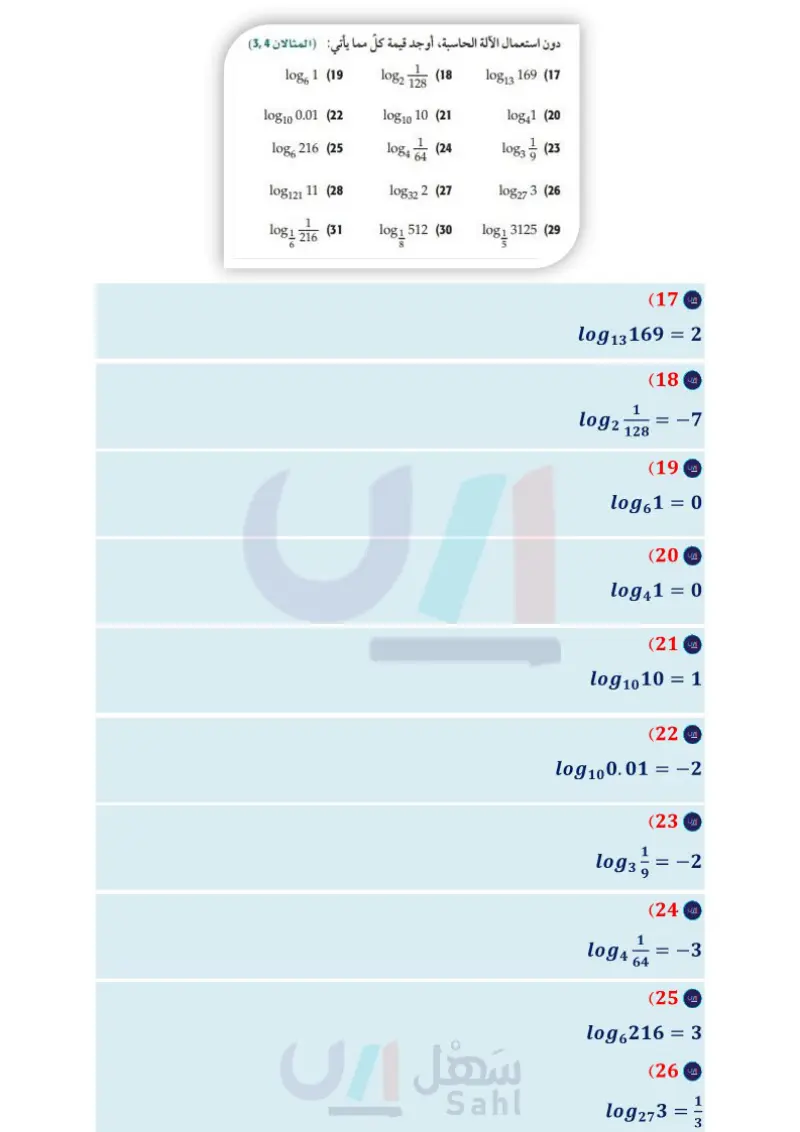
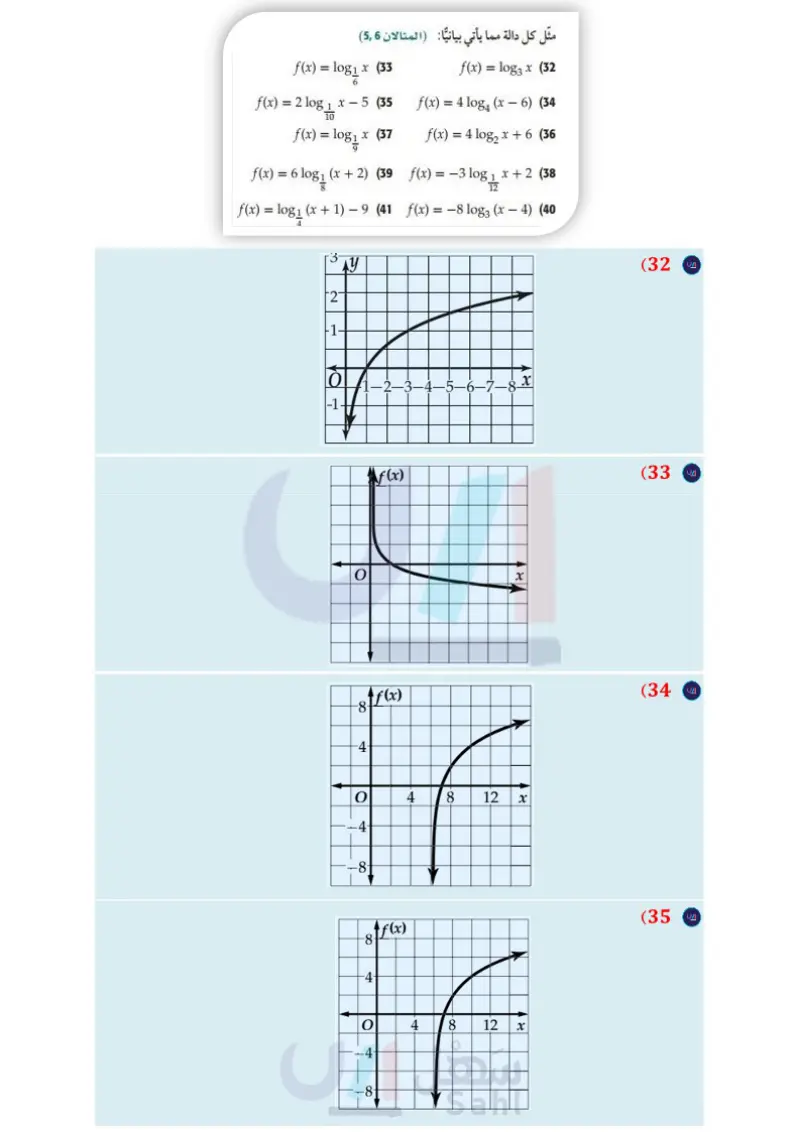
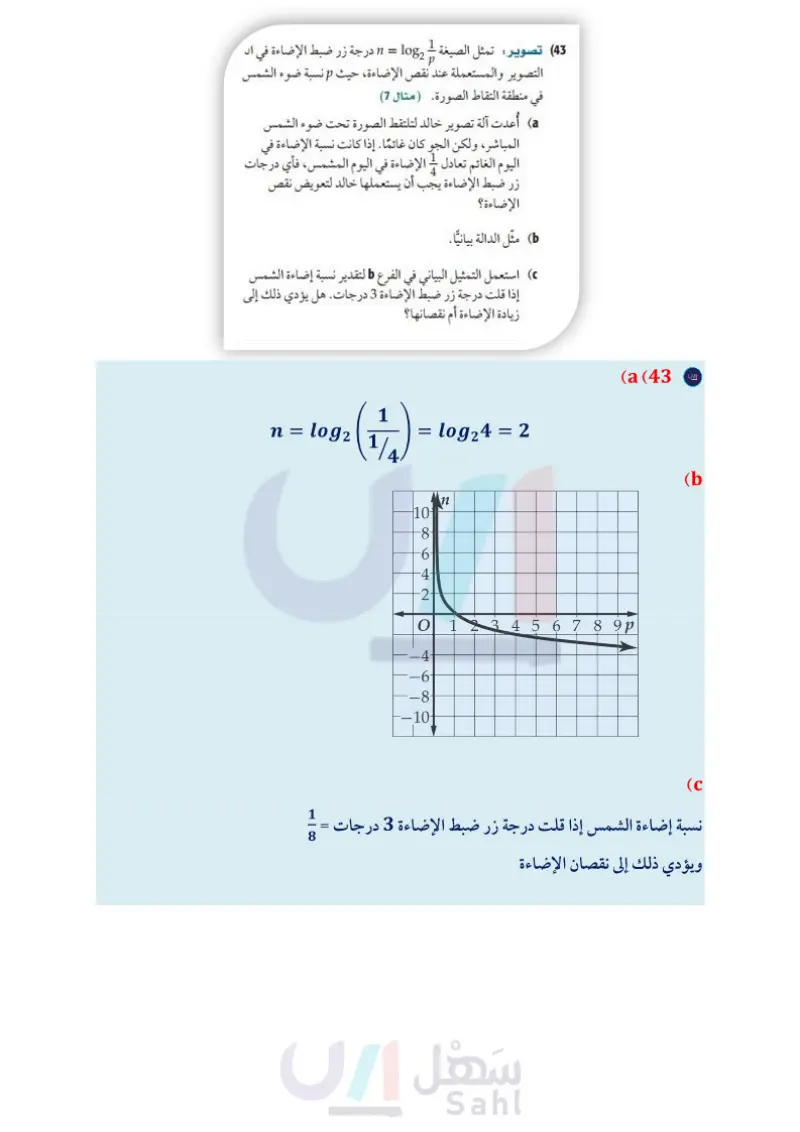
تدرب وحل المسائل اكتب كل معادلة لوغاريتمية مما يأتي على الصورة الأسية (مثال (1) (43) تصوير : تمثل الصيغة - 1082 = 1 درجة زر ضبط الإضاءة في آلة logg 512 = 3 (1 log5 625 = 4 (2 log7 343 = 3 (4 log2 16 = 4 (3 1 -3 (6 log9 -2 (5 81 log12 144 = 2 (7 = log3 1 27 = log, 1=0 (8 1 p التصوير والمستعملة عند نقص الإضاءة، حيث p نسبة ضوء الشمس في منطقة التقاط الصورة. ( مثال 7) أُعدت آلة تصوير خالد لتلتقط الصورة تحت ضوء الشمس المباشر، ولكن الجو كان غائمًا . إذا كانت نسبة الإضاءة في اليوم الغائم تعادل - الإضاءة في اليوم المشمس، فأي درجات زر ضبط الإضاءة يجب أن يستعملها خالد لتعويض نقص الإضاءة؟ مثل الدالة بيانيا . اكتب كل معادلة أسية مما يأتي على الصورة اللوغاريتمية (مثال (2) 113 = 1331 (9 9-1 = 1 | | (11 9 28 = 256 (13 2739 (15 (12 1648 (10 6-3 46 = 252 = 1 216 = 125 (16 = 4096 (14 دون استعمال الآلة الحاسبة، أوجد قيمة كل مما يأتي: (المثالان 3,4) استعمل التمثيل البياني في الفرع التقدير نسبة إضاءة الشمس إذا قلت درجة زر ضبط الإضاءة 3 درجات. هل يؤدي ذلك إلى زيادة الإضاءة أم نقصانها؟ يتم . عادة (44) تربية لقياس مدى احتفاظ الطلاب بالمعلومات اختبارهم بعد وقت من تعلمها، ويمكن تقدير درجة سلمان في مادة الرياضيات بعد انتهاء الفصل الدراسي باستعمال المعادلة (1) + 6og2 (t - 85 = ) ، حيث t عدد الأشهر التي مضت بعد انتهاء الفصل الدراسي. ما درجة سلمان في نهاية الفصل الدراسي (0 = ) ؟ 1 log 61 (19 10g2 (18 log13 169 (17 128 log 10 0.01 (22 log 10 10 (21 log41 (20 1 log6 216 (25 1084 (24 64 10839 3 (23) log121 11 (28 1081 216 log 32 2 (27 log 273 (26 1 (31 log1 512 (30 log 1081 3125 (29) مثل كل دالة مما يأتي بيانيا المثالان (56) f(x) = log3x (32 f(x) = log₁x (37 f(x) = log₁x (33 f(x) = 2 log 1 x -5 (35 10 9 - f(x) = 4 log (x — 6) (34 f(x) = 4 log2 x +6 (36 f(x) = 6 log₁ (x + 2) (39 f(x) = -3 log 1 x + 2 (38 12 f(x) = log₁ (x + 1) − 9 (41 f(x) = −8 log3 (x − 4) (40 4 (42 علوم عُد إلى فقرة "لماذا؟" بداية الدرس. أوجد معكوس الدالة اللوغاريتمية المعطاة ( مثال (7) ما درجته بعد مضي 3 أشهر؟ ما درجته بعد مضي 15 شهرًا؟ (45) مثل الدالة 9 - 1 + f(x) = 1510g14 x بيانيًا. (46) تحليليا اكتب معادلة لدالة يكون تمثيلها البياني يشبه التمثيل البياني للدالة y = 1083 x بعد إزاحتها 4 وحدات إلى اليسار ووحدة إلى أعلى. (47) إعلانات تزداد المبيعات عادة مع زيادة الإنفاق على الدعاية والإعلان، وتقدر قيمة المبيعات لشركة بآلاف الريالات بالمعادلة، (1) + a) = 10 + 20log (a) ، حيث a المبلغ الذي يتم إنفاقه على الدعاية والإعلان بآلاف الريالات، 0 < a . (a a تعني القيمة 10 (0) أنه إذا لم يُنفق شيء على الدعاية والإعلان، ستكون المبيعات 10000 ريال. أوجد كلّا من: (63) S (3), S (15), S. فسر معنى كل من القيم التي أوجدتها في الفرع a. مثل الدالة بيانيا. استعمل التمثيل البياني في الفرع ، ، وإجابتك في الفرع a لتفسير تناقص أثر الدعاية عند إنفاق مبالغ كبيرة عليها . وزارة التعليم 100 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية Ministry of Education 2024-1446

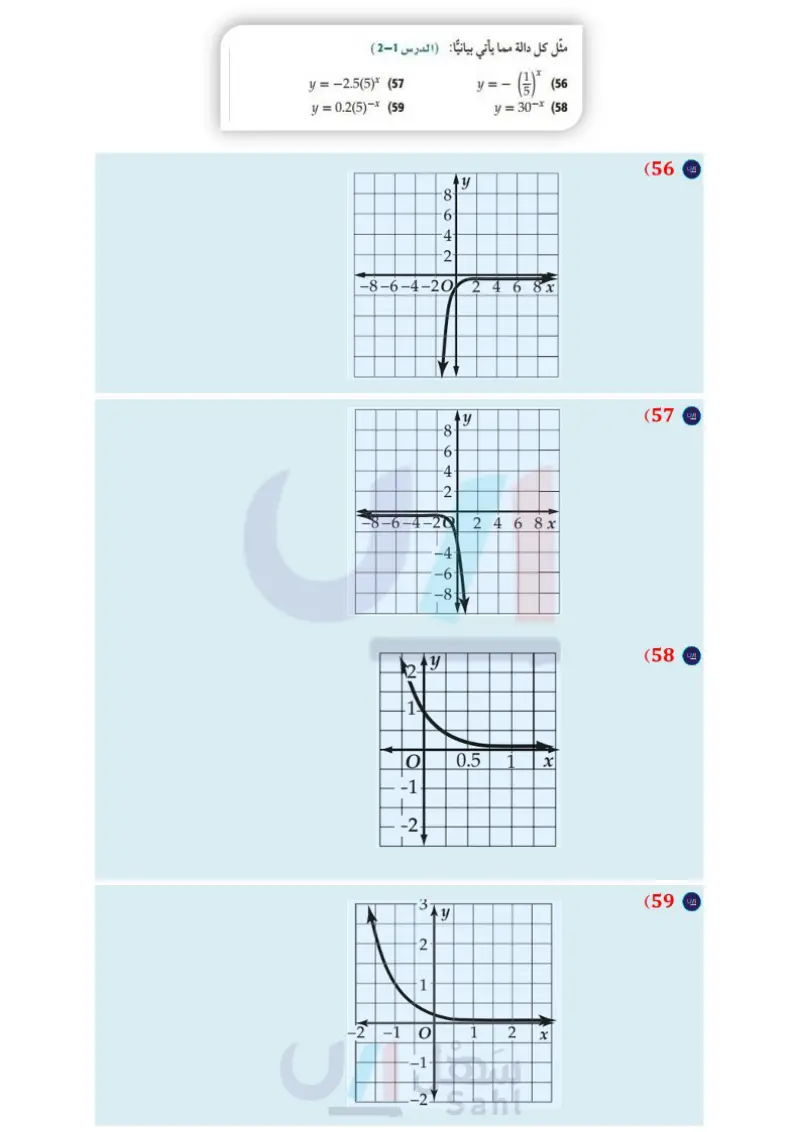
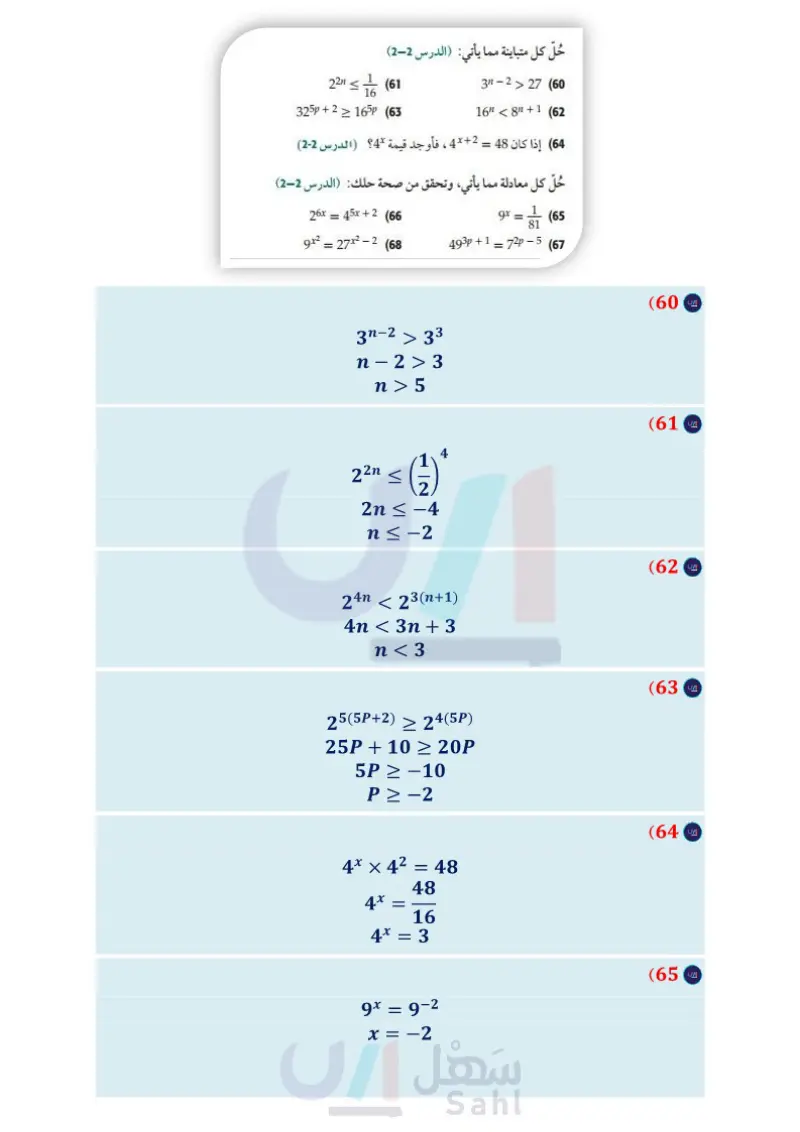
48 أحياء زمن الجيل بالنسبة للخلايا البكتيرية هو الزمن اللازم ليصبح عددها مثلي ما كان عليه . فإذا كان زمن الجيل G لنوع معين من البكتيريا يُعطى بالصيغة G، حيث t الفترة الزمنية t 3.3 log₁ ƒ = b عدد الخلايا البكتيرية عند بداية التجربة، أعدد الخلايا البكتيرية عند نهاية التجربة. يبلغ زمن الجيل لبكتيريا مجهرية ، 16 ، ما الزمن الذي تحتاج إليه 4 خلايا بكتيرية من هذا النوع ليصبح عددها 1024 ؟ إذا كان زمن الجيل لنوع من البكتيريا المخبرية 5، فما الوقت الذي تحتاج إليه 20 خلية بكتيرية من هذا النوع ليصبح عددها 160000 خلية ؟ تتكاثر بكتيريا E.coli بسرعة، بحيث تتكاثر 6 منها لتصبح 1296 خلال 4.4 . احسب زمن الجيل لبكتيريا E.coli . (53 تبرير دون استعمال الآلة الحاسبة، بين أي القيم التالية أكبر، وبرّر إجابتك : 71 و18 ,61 log7 51, logs 54 مسألة مفتوحة : اكتب عبارة لوغاريتمية على الصورة y = 10gb x لكل من الحالات الآتية: y a تساوي 25 y b عدد سالب بين 0 و 1 x (d تساوي 1 (55) اكتب إذا كان x) = alg) تحويلا للدالة : (a log10 (x - h اللوغاريتمية 10810 ، فاشرح كيفية تمثيل هذا التحويل بيانيًّا. 6 مراجعة تراكمية مسائل مهارات التفكير العليا (49) اكتشف المختلف: حدد العبارة المختلفة عن العبارات الثلاث مثل كل دالة مما يأتي بيانيا (الدرس 1-2 ) y = -2.5(5)* (57 y = 0.2(5)-* (59 X (56 الأخرى؟ فسر إجابتك. y = 30-x (58 1084 16 10g, 16 10g2 4 log3 9 (50) تحد : إذا كان y = log x ، حيث x, y أعداد حقيقية، فإن الصفر ينتمي إلى المجال دائمًا أو أحيانًا أو لا ينتمي أبدًا. وضح إجابتك. (51) اكتشف الخطأ : يقول فهد إن التمثيل البياني لجميع الدوال حُلّ كل متباينة مما يأتي: (الدرس (2-2) 3n-227 (60 16" 8" +1 (62 2211 ≤11 (61 22n< 16 325p+2165p (63 (64) إذا كان 48 = 2 + 4x ، فأوجد قيمة 4 (الدرس (2-2) اللوغاريتمية يقطع المحور ) في النقطة ) ؛ لأن أي عدد مرفوع حُلّ كل معادلة مما يأتي وتحقق من صحة حلك : (الدرس (2-2) للأس صفر يساوي ،1 ولكن سليمان لم يوافقه الرأي. أيهما على صواب؟ فسر إجابتك. (52) اكتشف الخطأ : أوجدت كل من مها ومريم قيمة 49 1081، منهما إجابتها صحيحة ؟ برر إجابتك. 7 81 26x = 45x + 2 (66 45x+2 1 9x = (65 = 9x227x2-2 (68 493p + 1 = 72p-5 (67 2 D -5 D 43 15 تدريب على اختبار (69) ما قيمة x في المعادلة logg 16 = x؟ C - c y ؟ 3.D 20 34 15 B B flog2 1 32 12 A (70) ما قيمة 5A 71) ما مقطع y للدالة الأسية 1 – × 4 = 1 B وزارة التعليم الدرس 3-2 اللوغاريتمات والدوال اللوغاريتمية Edu Min101 2024-1446 O A ريم log₁49 = y =49 (7-1)=72 (7)-4=72 y = -2 مها ا = 49, وما ラ 49% = 1 (7²)=(7) 721 = (7) 2y = - 1 1 y = - 2 -1

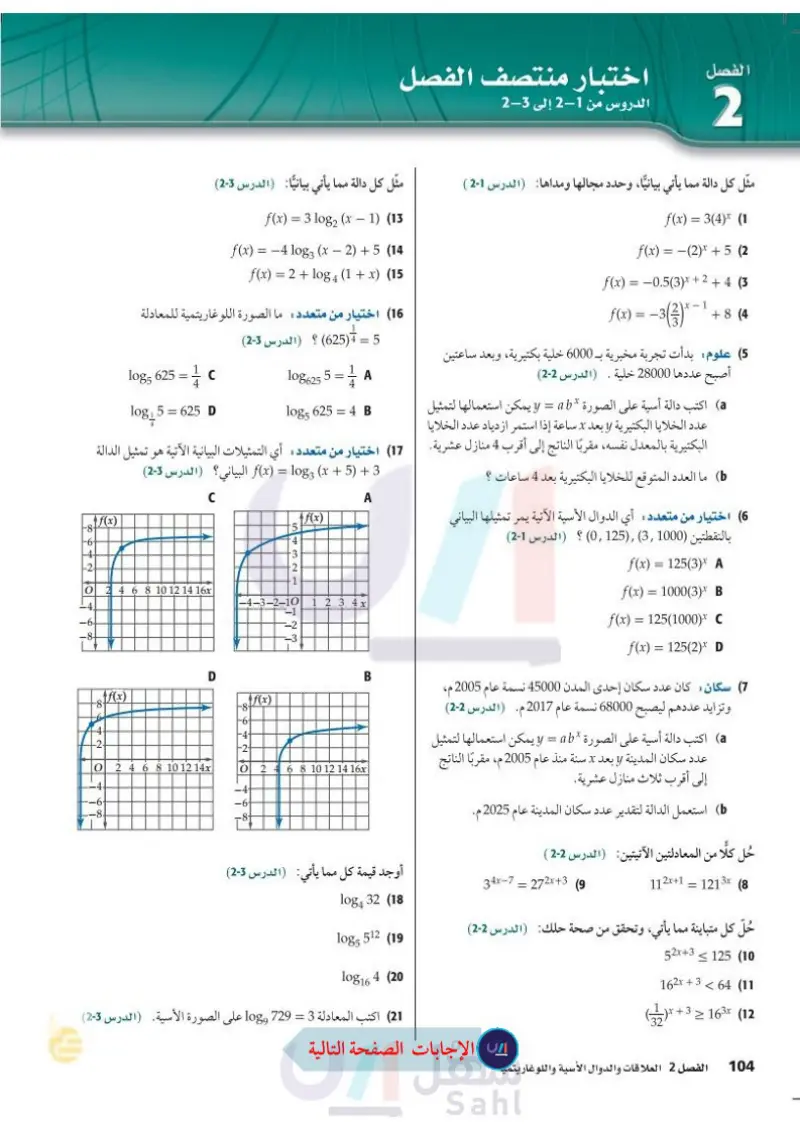
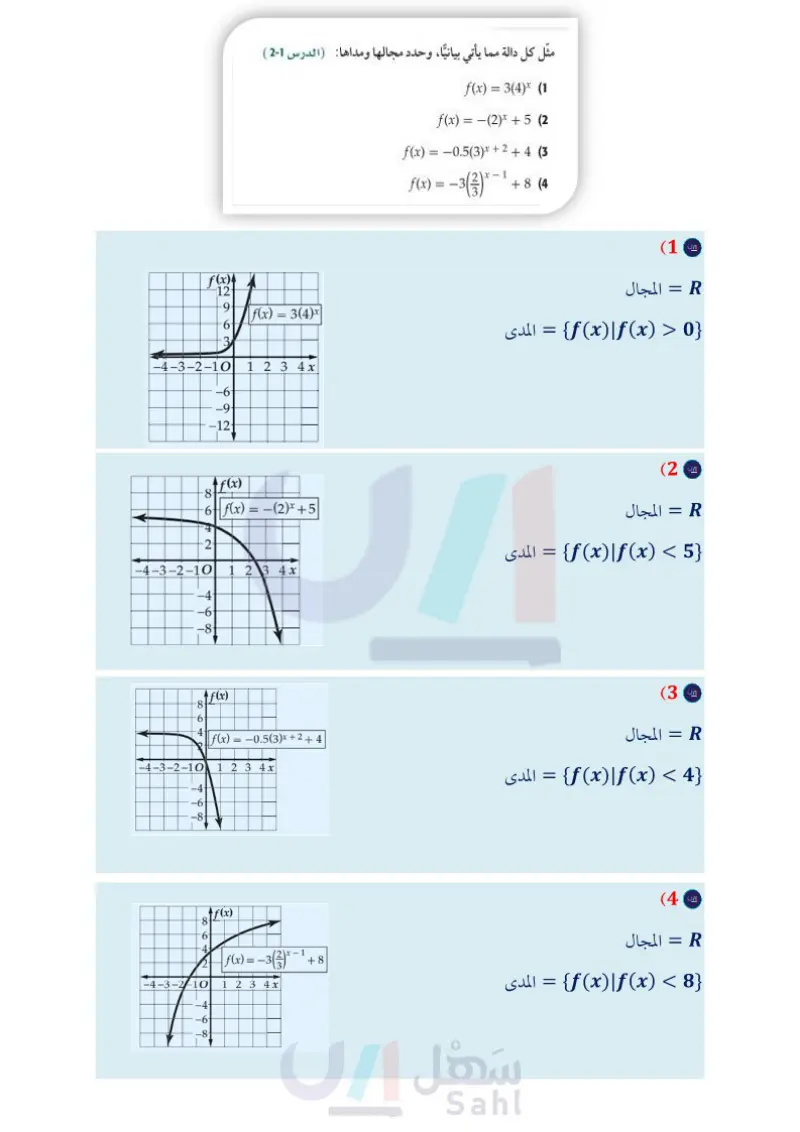
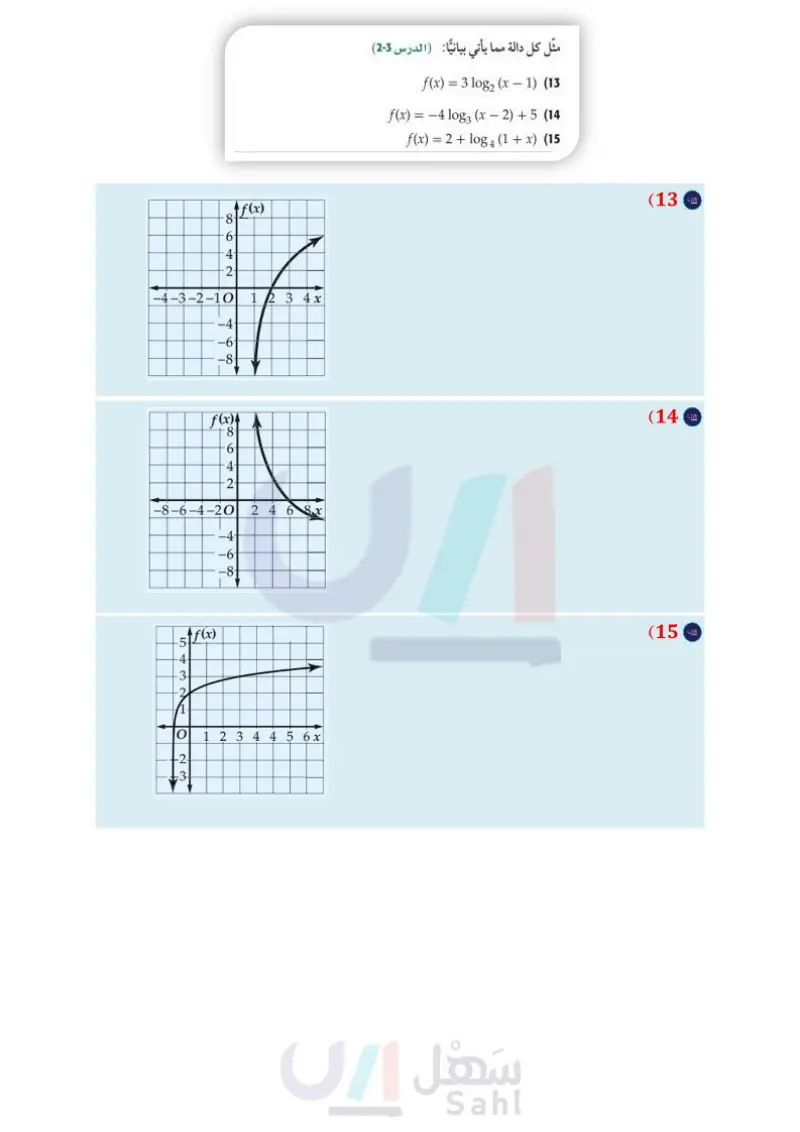
اختبار منتصف الفصل الدروس من 1-2 إلى 3-2 مثل كل دالة مما يأتي بيانيا (الدرس (3-2) f(x) = 3 log2 (x − 1) (13 f(x) = -4 log3 (x-2)+5 (14 f(x) = 2 + log4 (1 + x) (15 الفصل 2 مثل كل دالة مما يأتي بيانيًا، وحدد مجالها ومداها : ( الدرس 1-2 ) f(x) = 3(4)x (1 f(x) = −(2)x +5 (2 f(x) = -0.5(3)x + 2 + 4 (3 ƒ(x) = −3(¾³)* · +8 (4 (5) علوم : بدأت تجربة مخبرية بـ 6000 خلية بكتيرية، وبعد ساعتين أصبح عددها 28000 خلية (الدرس (2-2) a اكتب دالة أسية على الصورة * y = ab يمكن استعمالها لتمثيل عدد الخلايا البكتيرية y بعد x ساعة إذا استمر ازدياد عدد الخلايا (16) اختيار من متعدد : ما الصورة اللوغاريتمية للمعادلة 5 = 4 (625) ؟ (الدرس (3-2) 108625 5 = 1 5 = A 1085 625 = 4 B log5 625 = C log₁5 = 625 D (17) اختيار من متعدد: أي التمثيلات البيانية الآتية هو تمثيل الدالة البكتيرية بالمعدل نفسه، مقربًا الناتج إلى أقرب 4 منازل عشرية. ما العدد المتوقع للخلايا البكتيرية بعد 4 ساعات ؟ (6) اختيار من متعدد : أي الدوال الأسية الآتية يمر تمثيلها البياني بالنقطتين (31000) (15) الدرس (21) ' f(x) = 125(3)* A f(x) = 1000(3)* B f(x) = 125(1000) * C 3 + 5 + f(x) = 103 x البياني؟ (الدرس (3-2) A f(x) 5 2 L327 C f(x) -8- 2 4 6 8 10 12 14 16x 1 -4-3-2-10 1 2 3 4 x -1 -3 ناه من 10 -4- -2. O -4. -6- -8- f(x) -8- 4 نه الله D O2 4 6 8 10 12 14x -4- -6- -8- B f(x) = 125(2) D (7) سكان كان عدد سكان إحدى المدن 45000 نسمة عام 1995م، (الدرس (2-2) و تزايد عددهم ليصبح 68000 نسمة عام 2007 م. a اكتب دالة أسية على الصورة * y = ab يمكن استعمالها لتمثيل عدد سكان المدينة y بعد x سنة منذ عام 1995م، مقربًا الناتج إلى أقرب ثلاث منازل عشرية. استعمل الدالة لتقدير عدد سكان المدينة عام 2015م. حل كلًّا من المعادلتين الآتيتين: (الدرس 2-2 ) 112x+1=1213x (8 34x-7=272x+3 (9) حلّ كل متباينة مما يأتي، وتحقق من صحة حلك (الدرس (2-2) 52x+3125 (10 8- +f(x) 2 4 6 8 10 12 14 16x 8642 2 -6 -8- أوجد قيمة كل مما يأتي: (الدرس (3-2) log4 32 (18 log5 512 (19 log16 4 (20 (21) اكتب المعادلة 3 = 729 log على الصورة الأسية (الدرس (3-2) وزارة التعليم Ministry of Education 2024-1446 32 162364 (11 1x + 3 ≥ 163x (12 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 102




 0
0