العلاقات والدوال العكسية - رياضيات1-3 - ثالث ثانوي
الفصل الأول: تحليل الدوال
الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
نشاط الفصل الأول: تحليل الدوال
نشاط الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
رابط الدرس الرقمي www.ien.edu.sa العلاقات والدوال العكسية Inverse Relations and Functions 1-7 فيما سبق: درستُ إيجاد تركيب دالتين. (الدرس 6-1) والآن : أستعمل اختبار الخط الأفقي على منحنى الدالة لتحديد إن كان لهذه الدالة دالة عكسية أم لا. أجد الدالة العكسية جبريًا وبيانيا. المفردات: العلاقة العكسية inverse relation الدالة العكسية inverse function الدالة المتباينة لماذا ؟ يربط الجدول A عدد تذاكر دخول مدينة ألعاب بسعرها، في حين يربط الجدول B السعر بعدد التذاكر. لاحظ أن تبديل صفي الجدول A يُعطي الجدول B. الجدول A عدد التذاكر السعر بالريال LO 5 2 4 3 1 5 10 15 20 25 الجدول B السعر بالريال عدد التذاكر 15 10 5 2 1 3 25 20 20 ما 5 4 الدالة العكسية : العلاقة في الجدول A تمثل علاقة عكسية للعلاقة في الجدول .B. يقال: إن كلا من العلاقتين A, B علاقة عكسية للأخرى إذا وفقط إذا تحقق الشرط التالي: إذا كان الزوج المرتب ) ينتمي إلى إحدى العلاقتين؛ فإن الزوج المرتب (b) ينتمي إلى العلاقة الأخرى. وإذا مُثَّلت العلاقة بمعادلة، فيمكن إيجاد علاقتها العكسية بتبديل المتغير المستقل بالمتغير التابع، فمثلا العلاقة y = x2 - 4 one-to-one function العلاقة العكسية 4 - x = y2 أو 4 + y2 = x - x LO 5 y -3 بی y x -3 ما 5 0 -2 y = x 2 - 4 -2 0 -3 -1 -1 -3 x -4 0 0 -4 y = x -3 1 1 -3 2 0 2 | y = x + 4 2 0 5 3 3 5 قراءة الرياضيات رمز الدالة العكسية : الا يجب يحدث لبس بين رمز الدالة العكسية (f -1(x ومقلوب الدالة (f(x _ 1. لاحظ أن كل علاقة من هاتين العلاقتين المتعاكستين هي انعكاس للأخرى حول المستقيم y = x . هذه العلاقة صحيحة بين كل منحنيات العلاقات ومنحنيات علاقاتها العكسية. يتضح من تعريف العلاقة العكسية أنه لكل علاقة يوجد علاقة عكسية، إلا أن اهتمامنا ينصب على الدوال التي تمثل علاقاتها العكسية دوال. فإذا كانت العلاقة العكسية لدالة تمثل دالة سميت الدالة العكسية لـ f، ويرمز لها بالرمز 1-f . لاحظ في التمثيل البياني أعلاه أن العلاقة الأصلية دالة؛ لأنها تحقق اختبار الخط الرأسي، إلا أن علاقتها العكسية لا تحقق هذا الاختبار فهي ليست دالة. وبشكل عام، ليس من الضروري أن تكون العلاقة العكسية دالة. يقودنا تمثيل العلاقة وعلاقتها العكسية إلى اختبار آخر لتحديد وجود دالة عكسية. مفهوم أساسي اختبار الخط الأفقي التعبير اللفظي: يوجد للدالة دالة عكسية 1- f إذا وفقط إذا كان كل خط أفقي يتقاطع مع منحنى الدالة عند نقطة واحدة على الأكثر. نموذج مثال : بما أنه لا يوجد خط أفقي يقطع منحنى الدالة f بأكثر من نقطة، فإن الدالة العكسية 1-f موجودة. y= f(x) 0 x وزارة التعليم Ministry of Education 2024-1446 الفصل 1 تحليل الدوال 64

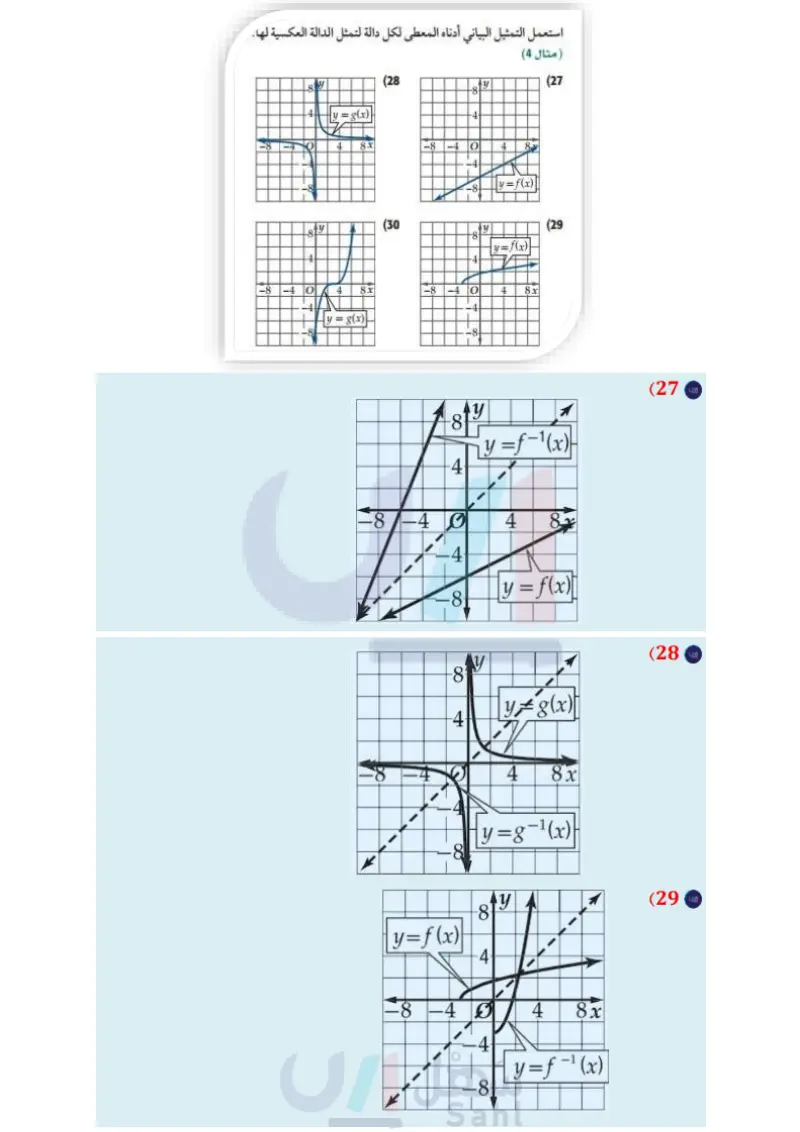
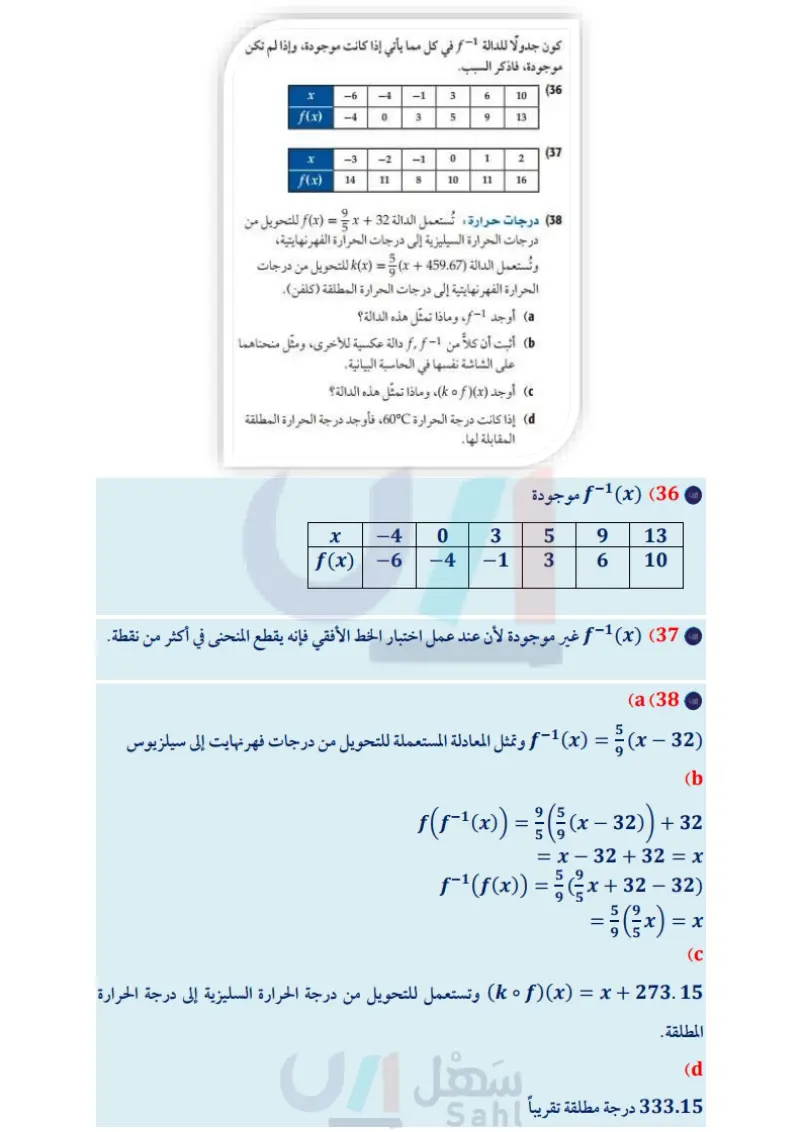
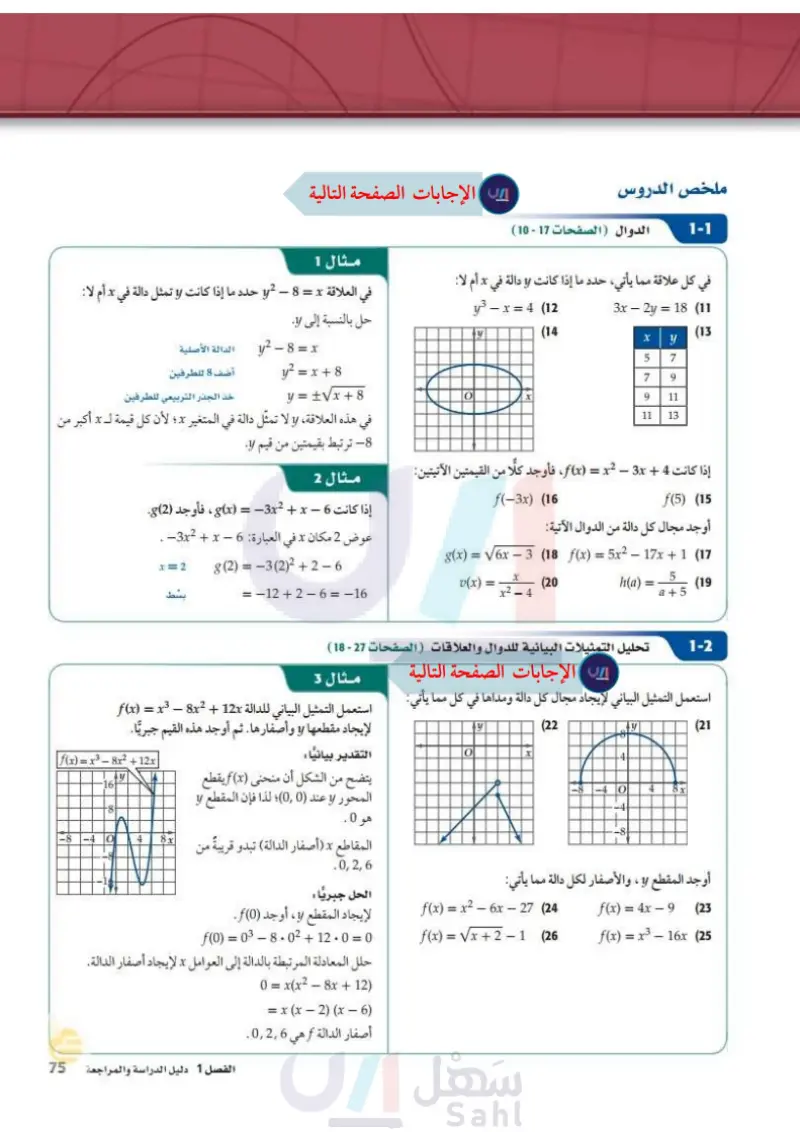
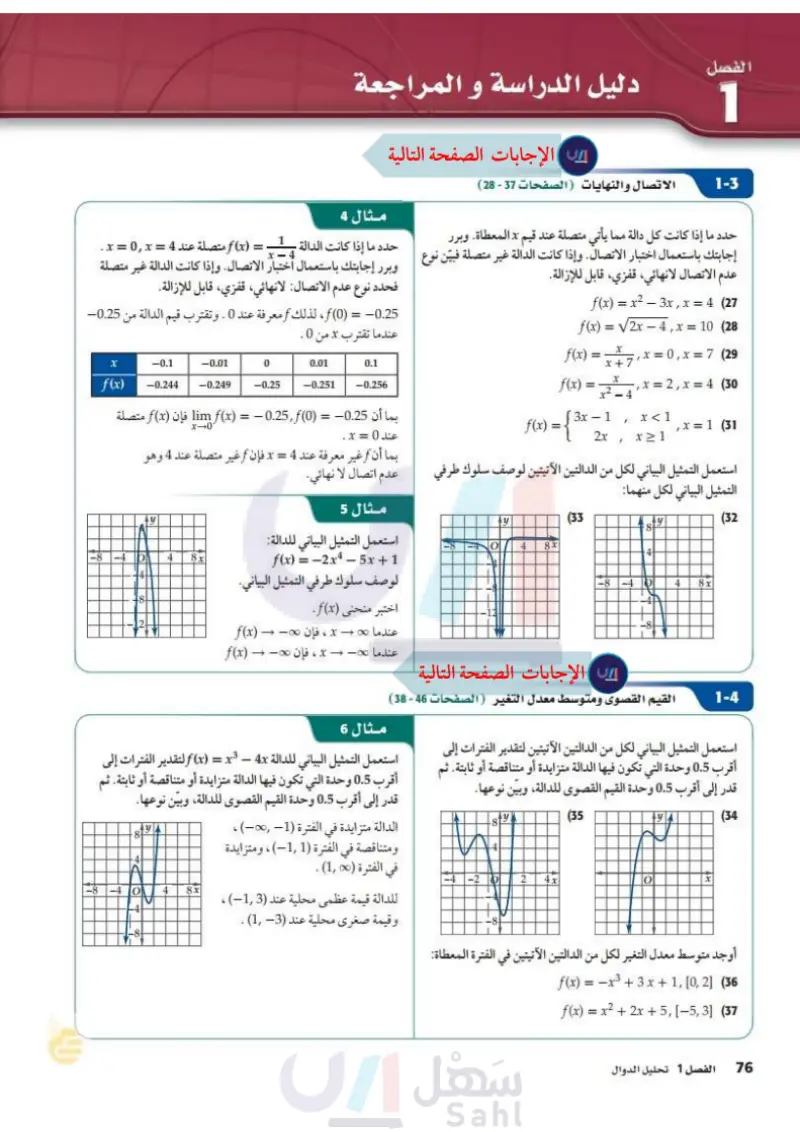
استعمل اختبار الخط الأفقي على منحنى الدالة لتحديد إن كان لهذه الدالة دالة عكسية أم لا.
رمز الدالة العكسيه
تنبيه! اختبار الخط الأفقي عند استعمال الحاسبة البيانية، اختبر بدقة المواقع التي يفشل فيها اختبار الخط الأفقي باستعمال 4 تكبير/تصغير النافذة واختر منها مثال 1 تطبيق اختبار الخط الأفقي مثل كلا من الدوال الآتية بيانيًا باستعمال الحاسبة البيانية، ثم طبق اختبار الخط الأفقي لتحديد إن كانت الدالة العكسية موجودة أم لا. f(x) = |x − 1| (a - يوضّح التمثيل البياني للدالة في الشكل المجاور أنه من الممكن إيجاد خط أفقي يقطع منحنى (f(x في أكثر من نقطة، وعليه فإن 1-f *65-1 1.1 f1(x)=|x-1| 6.677 -10 -6.67 65-2 6.67 y 1.1 10 1 -10 10 -6.67 1(x)=x³-6 x²+12-x-8 غير موجودة. g(x) = x³ — 6x² + 12x−8 (b - يوضح التمثيل البياني للدالة (x) في الشكل المجاور أنه من غير الممكن إيجاد خط أفقي يقطع منحنى الدالة (x) في أكثر من نقطة، وعليه فإن 1-g موجودة. f(x) = x2 + 5x - 7 (18 تحقق من فهمك h(x) = 4 (IA إيجاد الدالة العكسية إذا حققت الدالة اختبار الخط الأفقي سُميت دالة متباينة؛ لأن كل قيمة لـ x ترتبط بقيمة : واحدة فقط لـ y. ولا توجد قيمة لـ لا ترتبط بأكثر من قيمة لـ x. إذا كانت الدالة متباينة، فإن لها دالة عكسية على أن يكون مجال f مساويا لمدى 1 f ومدى مساويا لمجال 1-f . مجال f Xx f(x). -f-¹(x)· مدى f f(x) مجال 1-f لإيجاد الدالة العكسية جبريا، نتبع الخطوات الآتية: مفهوم أساسي إيجاد الدالة العكسية مدى 1-f الخطوة 1 تحقق من وجود دالة عكسية للدالة المعطاة بالتحقق من أنها متباينة بالاعتماد على اختبار الخط الأفقي. الخطوة 2: ضع لا مكان (f(x ، ثم بدل موقعي x, y . الخطوة 3 حل المعادلة بالنسبة للمتغير ، ل ، ثم ضع (f-1(x مكان y . الخطوة 4 اذكر أية شروط على مجال 1 f . وبيّن أن مجال أ يساوي مدى -1- f، وأن مدى أيساوي مجال 1-f . يظهر من الخطوة الأخيرة أن جزءًا فقط من الدالة التي أوجدتها جبريًّا قد يكون دالة عكسية للدالة ؛ لذا يجب دراسة مجال أ عند إيجاد 1 f . وزارة التعليم الدرس 7-1- العلاقات والدوال العكسية M65 of E 2024-1446 3 تكبير 4: تصغير أو اضبط الشاشة للتأكد.

1A- مثل كل من الدوال الآتية بيانيا باستعمال الحاسبة البيانية، ثم طبق اختبار الخط الأفقي لتحديد إن كانت الدالة العكسية موجودة أم لا.


اختبار الخط الافقي
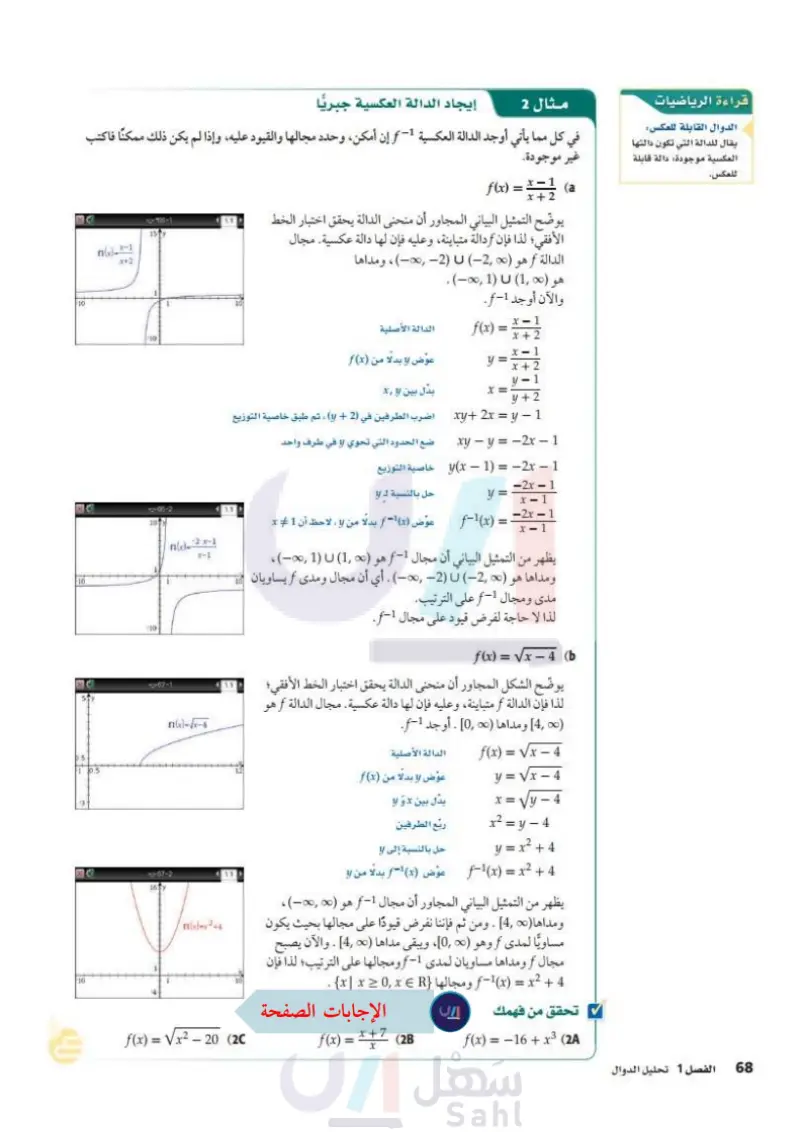
قراءة الرياضيات الدوال القابلة للعكس : مثال 2 إيجاد الدالة العكسية جبريًا - في كل مما يأتي أوجد الدالة العكسية 1 f إن أمكن، وحدد مجالها والقيود عليه، وإذا لم يكن ذلك ممكنا فاكتب يقال للدالة التي تكون دالتها 10 Te 10 *66-1 1.1 15 y f(x)= X-1 51y 0.5 -1 10.5 -3 11 10 x+2 وزارة التعليم Ministry of Education 2024-1446 -10 -66-2 10 y f1(x)=¨²¨ x−1 -10 767-1 x-1 f1(x)=√(x-4 العكسية موجودة دالة قابلة غير موجودة. للعكس. f(x) = 1 X- (a x+2 يوضح التمثيل البياني المجاور أن منحنى الدالة يحقق اختبار الخط الأفقي ؛ لذا فإن أدالة متباينة، وعليه فإن لها دالة عكسية. مجال الدالة f هو (2,0) U (2 ,0) ، ومداها الدالة الأصلية عوض لا بدلًا من (f(x بدل بين x اضرب الطرفين في (2) + ) ، ثم طبق خاصية التوزيع ضع الحدود التي تحوي لا في طرف واحد 1.1 1.1 -67-2 1.1 167y f1(x)=x²+4 . (−∞, 1) U (1, ∞) es هو والآن أوجد 1-f. f(x) x-1 = x+2 x 1 y = x+2 y - 1 x = xy+ 2x = y - 1 y +2 xy - y = -2x - 1 1 - x - 1 = -2x) خاصية التوزيع حل بالنسبة لـ y عوض (f (x بدلا من y ، لاحظ أن 1 # x y = f-1(x) = -2x-1 x-1 -2x-1 x-1 يظهر من التمثيل البياني أن مجال 1 f هو (1) U (1) ومداها هو (2) (2) . أي أن مجال ومدى f يساويان مدى ومجال 1-f على الترتيب. لذا لا حاجة لفرض قيود على مجال 1-f . 10 f(x) = Vx - 4 (b يوضح الشكل المجاور أن منحنى الدالة يحقق اختبار الخط الأفقي؛ لذا فإن الدالة f متباينة، وعليه فإن لها دالة عكسية. مجال الدالة f هو 4,00] ومداها (0 ,0] . أوجد 1-f الدالة الأصلية f(x) = Vx - 4 y = Vx 4 x = Vy - 4 x2 = y - 4 y = x2 + 4 f-1(x) = x2 + 4 عوض لا بدلا من (f(x بدل بين x و لا ربع الطرفين حل بالنسبة إلى ل عوض (f(x بدلا من لا يظهر من التمثيل البياني المجاور أن مجال 1-f هو (0 ,0) ، ومداها (4] . ومن ثم فإننا نفرض قيودًا على مجالها بحيث يكون مساويًا لمدى f وهو ( 0]، ويبقى مداها ( 4] . والآن يصبح مجال f ومداها مساويان لمدى -1- أ ومجالها على الترتيب؛ لذا فإن 4 + f(x) = x2 ومجالها x | x ≥ 0, x E R} . تحقق من فهمك f(x) = √x² - 20 (2C f(x) = x+7 (2B f(x) = −16 + x3 (2 x الفصل 1 تحليل الدوال 66

الدوال القابلة للعكس
10 إن الدالة العكسية 1-f تلغي عمل الدالة f والعكس صحيح؛ لذا فإنه يمكننا تعريف الدوال العكسية باستعمال عملية التركيب بينهما. مفهوم أساسي تركيب الدالة ودالتها العكسية تكون كل من الدالتين أو 1 - f ، دالة عكسية للأخرى، إذا وفقط إذا تحقق الشرطان الآتيان: • f [f - (x] = x لجميع قيم x في مجال (f(x . • f - f(x)] = x لجميع قيم x في مجال (f(x . لاحظ أن تركيب f و 1-f هو الدالة المحايدة. وتُستعمل هذه الحقيقة للتحقق من أن كلا من الدالتين دالة عكسية للأخرى. مثال 3 إثبات أن كل دالة تمثل دالة عكسية للأخرى أثبت جبريًا أن كلًا من الدالتين = (f(x و 4 + g(x) = f دالة عكسية للأخرى 6 - 4 أثبت أن flg(x) = x و f(x)] = x] . 12(x)=4+ X -10 167 1.1 15 x f(x)= 6 6 x-4 6 8[f(x)] = 8 ( x 2 4 ) = 6 6 +4 x 4 = x - 4 + 4 = x flg(x)] = f (2 + 4 || || (4) +4 6 (2 + 4) - 4 6 = X X بما أن x] = [f(x)] = x)، فإن كلا من الدالتين (f(x),(x تكون دالة عكسية للأخرى. ويؤكد التمثيل البياني المجاور هذه الإجابة حيث تنتج كل دالة 1 من الأخرى بالانعكاس حول المستقيم y = x . تحقق من فهمك أثبت جبريًا أن كلا من الدالتين تمثل دالة عكسية للأخرى في كل مما يأتي: f(x) = x² + 10, x ≥0, g(x) = √√x − 10 (3B - f(x) = 18 — 3x, g(x) = 6 — — (3A إرشادات للدراسة الدالة العكسية والقيم القصوى يكون للدالة المتصلة دالة عكسية، إذا وفقط إذا لم يكن لها قيم عظمى أو صغرى محلية. فإذا كان للدالة قيم عظمى أو صغرى محلية فإن الدالة تفشل باختبار الخط الأفقي، ومن ثم لا تكون دالة متباينة. من الصعب إيجاد الدالة العكسية جبرياً لمعظم الدوال المتباينة، إلا أنه يمكننا تمثيل منحنى الدالة العكسية بانعكاس الدالة الأصلية حول المستقيم y = x . مثال 4 إيجاد الدالة العكسية بيانيا استعمل التمثيل البياني للدالة ( f ( x في الشكل 1.7.3 لتمثيل (f - 1 (x . مثل بيانيا المستقيم y = x . وعيّن بعض النقاط على منحنى (f(x. أوجد صور هذه النقاط بالانعكاس x. حول المستقيم y = x. ثم صل بينها بمنحنى كصورة في مرآة لمنحنى الدالة (f(x حول المستقيم y = x (الشكل 1.7.4). y = f(x) y V=X X y = f -1 (x) y |y = f(x) الشكل 1.7.3 الشكل 1.7.4 وزارة التعليم الدرس 7-1- العلاقات والدوال العكسية 67y of E 2024-1446 x

الدالة العكسية والقيم القصوى
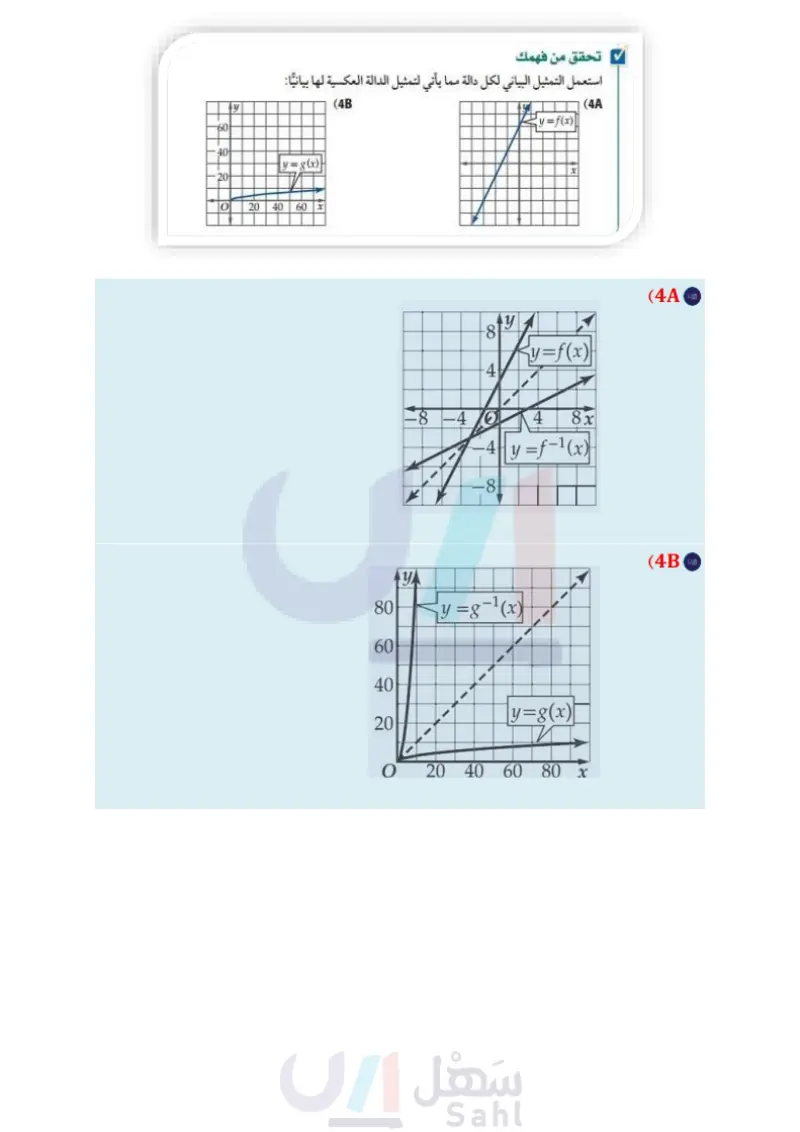
-60 40 40 Ay تحقق من فهمك استعمل التمثيل البياني لكل دالة مما يأتي لتمثيل الدالة العكسية لها بيانيا : 20 20 y = g(x) 20 O 60 40 x (4B (4A y = f(x) X الربط مع الحياة ينص نظام العمل في المملكة على أنه "لا يجوز تشغيل العامل تشغيلا فعليًّا أكثر من 8 ساعات في اليوم الواحد إذا اعتمد صاحب العمل المعيار اليومي أو أكثر من 48 ساعة إذا اعتمد المعيار الأسبوعي. مثال 5 من واقع الحياة استعمال الدالة العكسية من الساعات لا يقل عن 40 أعمال : يتقاضى شخص 16 ريالًا عن كل ساعة عمل، ويعمل في الأسبوع . سبوع عددًا ساعة ولا يزيد على 105 ساعات، ويتقاضى أجرًا إضافيًا مقداره 24 ريالًا عن كل ساعة عمل إضافية تزيد على الـ 40 ساعة. ويمكن حساب دخله الأسبوعي مقابل x ساعة عمل بالدالة 40 - f(x) = 640 + 24(x . أثبت أن (f(x موجودة، ثمّ أوجدها. يمكننا تبسيط الدالة لتصبح 960 - f(x) = 640 + 24x أو 320 - f(x) = 24x . يحقق منحنى الدالة (f(x اختبار الخط الأفقي؛ لذا فإن (f(xدالة متباينة، وعليه تكون دالتها العكسية موجودة. أوجد (f-1(x: f(x) = 24x - 320 y = 24x – 320 x = 24y – 320 x + 320 = 24y x + 320 الدالة الأصلية عوض لا بدلا من (f(x بدل بين x و y أضف 320 إلى الطرفين حل بالنسبة إلى ل الدخل الأسبوعي لعامل 100 x 50 y 2000 1500 1000 500 0 الدخل (بالريال) إرشادات للدراسة الدالة الخطية: يمكنك الحكم بأن منحنى الدالة الخطية يحقق اختبار الخط الأفقي دون الحاجة إلى رسمه. 24 x + 320 24 Y: = f-1(x) = عوض (x)1- أ بدلا من لا ماذا تمثل كل من x و (f -1 (x في الدالة العكسية؟ الزمن (بالساعات) في الدالة العكسية تمثل x الدخل الأسبوعي بالريال، وتمثل (f 1(x عدد ساعات العمل الأسبوعية. حدّد القيود المفروضة على مجال (f(x ومجال (x) 1- إن وجدت؟ وضّح إجابتك. الحد الأدنى لساعات العمل الأسبوعية هو 40 ساعة. والحد الأعلى 105 ساعات؛ لذا فإن مجال(f(x هو [105 ,40]. و بما أن 2200 (105)f(40) = 640, f ، فإن مدى (f(xهو [640,200] ، وهو مجال الدالة (f -1 (x . = أوجد عدد الساعات التي عملها الشخص في أسبوع كان دخله فيه 760 ريالًا. = 760 + 320 24 = 45 تحقق من فهمك : (1760 f أي أن الشخص عمل 45 ساعة في هذا الأسبوع. (5) توفير: يتبقى لأحمد بعد سداد أقساط منزله وبعض الالتزامات 65% من راتبه الشهري، فإذا خصص منها 1800 ريال لنفقات المعيشة، وقدّر أن بإمكانه توفير 20% من المبلغ المتبقي تقريبًا، فإن مقدار التوفير الشهري يعطى بالدالة: (1800 - f(x) = 0.2(0.65x، حيث x الراتب الشهري. (5) أثبت أن ( 1 - f موجودة، ثم أوجدها. (5) ماذا تمثل كل من ( 1 x, f في الدالة العكسية؟ 5) حدد أية قيود على كل من مجال (f(x) f(x إن وجدت. وبرّر إجابتك. 50) إذا وفّر أحمد 500 ريالًا في الشهر، فأوجد راتبه الشهري. وزارة التعليم Ministry of Education 2024-1446 الفصل 1 تحليل الدوال 68

ينص نظام العمل في المملكة على أنه "لا يجوز تشغيل العامل تشغيلا فعليا أكثر من 8 ساعات في اليوم الواجد"
الدالة الخطية
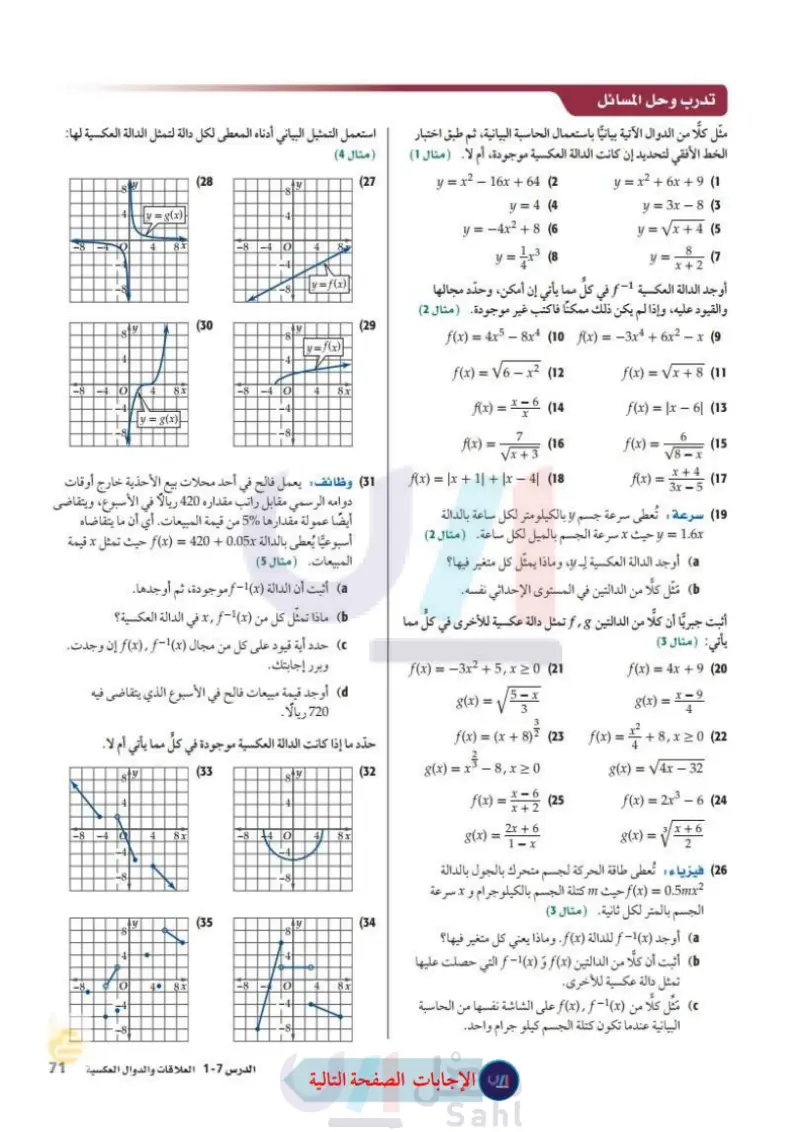
تدرب وحل المسائل استعمل التمثيل البياني أدناه المعطى لكل دالة لتمثل الدالة العكسية لها: مثل كلًا من الدوال الآتية بيانيًا باستعمال الحاسبة البيانية، ثم طبق اختبار ( مثال 4) الخط الأفقي لتحديد إن كانت الدالة العكسية موجودة، أم لا. (مثال (1) -4 8 y |y = g(x) (28 8+ y 4. -8 -4 O انی y 8 00 4 (27 y = x2 - 16x + 64 (2) y = 4 (4 y = −4x2 + 8 (6) 8x -8 -40 4 8 -4- y = 7r3 (8 H |y = g(x) 8x -8 |y = f(x) 10 (30 8 4 الله |y = f(x) -40 10+ -4- -8- 4 00. 8x (29 y = x2 + 6x + 9 (1) y = 3x - 8 (3) y = Vx + 4 (5 У = 8 x+2 (7 أوجد الدالة العكسية -1 f في كل مما يأتي إن أمكن، وحدد مجالها والقيود عليه، وإذا لم يكن ذلك ممكنا فاكتب غير موجودة (مثال (2) f(x) = 4x5 - 8x4 (10) f(x) = - 3x4 + 6x2 - x (9) f(x) = V6 - x2 (12) f(x) = Vx + 8 (11 f(x) = x=6 (14 Xx f(x) = |x − 6| (13 - 7 f(x) == (16 f(x) = Vx + 3 6 V8 (15 f(x) = |x + 1| + |x − 4| (18 f(x) = == - X x + 4 3x - 5 (17 31) وظائف يعمل فالح في أحد محلات بيع الأحذية خارج أوقات دوامه الرسمي مقابل راتب مقداره 420 ريالاً في الأسبوع، ويتقاضى (19) سرعة تُعطى سرعة جسم لا بالكيلومتر لكل ساعة بالدالة y = 1.6x أيضًا عمولة مقدارها 5% من قيمة المبيعات. أي أن ما يتقاضاه حيث * سرعة الجسم بالميل لكل ساعة (مثال (2) أوجد الدالة العكسية لـ y، وماذا يمثل كل متغير فيها؟ مثل كلا من الدالتين في المستوى الإحداثي نفسه. أثبت جبريًا أن كلا من الدالتين , f تمثل دالة عكسية للأخرى في كلّ مما يأتي: (مثال 3) g(x)= 5 X 3 2 f(x) = - 3x2 + 5 x 2 0 (21 f(x) = (x+8)² (23 g(x) = x3 - 8, x 2 0 x-6 f(x) = x (25 x + 2 f(x) = 4x + 9 (20) - 8(x) = x = 9 4 f(x) = # + 8, x 2 0 (22 4 g(x) = V4x - 32 f(x) = 2x3 - 6 (24) g(x) = 3/ x + 6 2 2x + 6 g(x) = 1-x أسبوعيًا يُعطى بالدالة f(x) = 420 + 0.05x حيث تمثل x قيمة المبيعات (مثال (5) a أثبت أن الدالة ( f ( x موجودة، ثم أوجدها. ماذا تمثل كل من (x, f(x في الدالة العكسية؟ حدد أية قيود على كل من مجال (1-f(x), f إن وجدت. وبرر إجابتك. d أوجد قيمة مبيعات فالح في الأسبوع الذي يتقاضى فيه 720 ريالًا. حدد ما إذا كانت الدالة العكسية موجودة في كل مما يأتي أم لا. (32 8 y 4 (33 819 -8 -4 Q 4 8x -8 140 4 8x -4 -4 8 -8- a y (35 y -8- -4 الله O 4• + 00 loo 8x ―4 وزارة التعليم الدرس 7-1- العلاقات والدوال العكسية of E 69 2024-1446 4 4 -4 -8 8x (34 (26) فيزياء : تُعطى طاقة الحركة لجسم متحرك بالجول بالدالة f(x) = 0.5mx2 حيث m كتلة الجسم بالكيلوجرام و xسرعة الجسم بالمتر لكل ثانية ( مثال (3) - ) أوجد ( f ( x للدالة ( f ( x . وماذا يعني كل متغير فيها؟ أثبت أن كلا من الدالتين (f(x و (f-1(x التي حصلت عليها تمثل دالة عكسية للأخرى. مَثْل كلا من (f(x), f(x على الشاشة نفسها من الحاسبة البيانية عندما تكون كتلة الجسم كيلو جرام واحد.

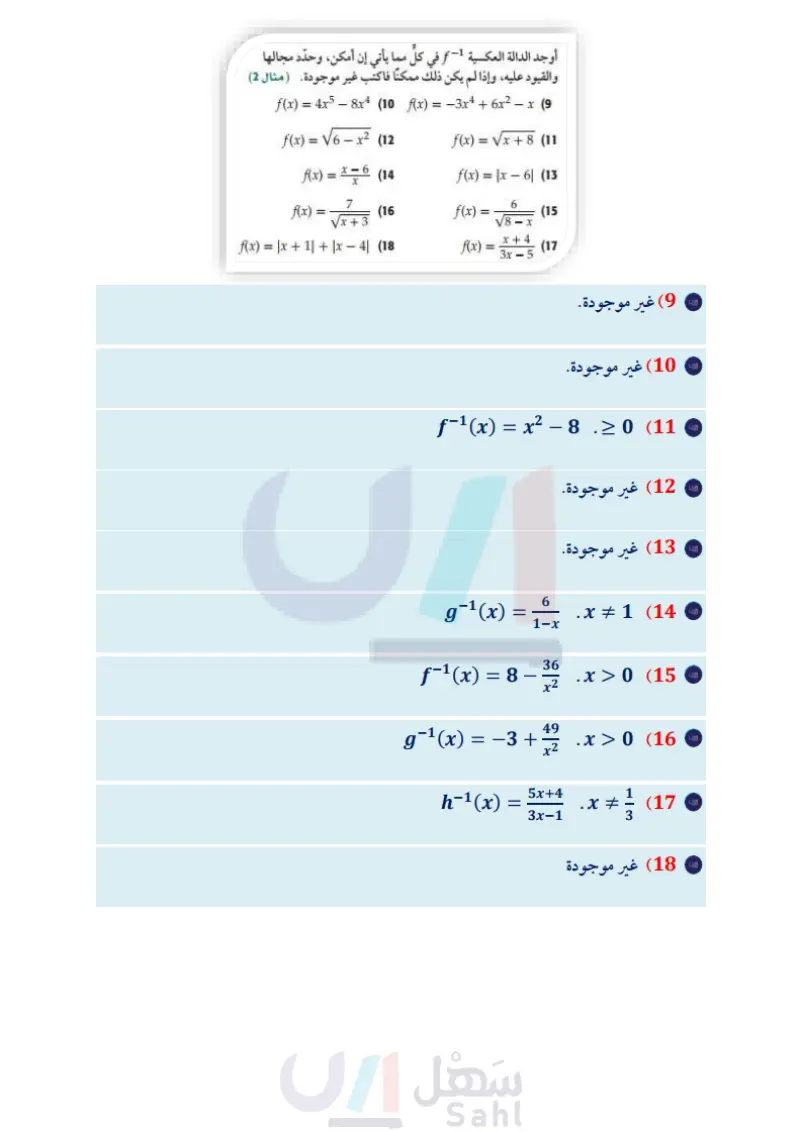
كون جدولًا للدالة 1- f في كل مما يأتي إذا كانت موجودة، وإذا لم تكن إذا كانت الدالة 1- f موجودة، فاكتب المجال والمدى لكل من 1- ff: موجودة، فاذكر السبب f(x) = Vx - 6 (44 f(x) = x2 + 9 (45 3x + 1 (36 x -6 -4 -1 3 6 10 f(x) -4 0 3 LO 5 9 13 f(x) = (46 X = 4 (37 x -3 -2 -1 0 1 2 8x + 3 f(x) = (47 f(x) 14 11 8 10 11 16 2x 6 9 5 38 درجات حرارة تُستعمل الدالة 32 + f(x) = 3 x للتحويل من أوجد الدالة العكسية في كل مما يأتي، إن أمكن، ثم مثل 1-f, f في مستوى إحداثي واحد و اذكر أية قيود على المجال: درجات الحرارة السيليزية إلى درجات الحرارة الفهرنهايتية، وتُستعمل الدالة (459.67 + k(x) = 3 x للتحويل من درجات الحرارة الفهرنهايتية إلى درجات الحرارة المطلقة (كلفن). أوجد 1 f، وماذا تمثل هذه الدالة؟ أثبت أن كلاً من -1 f f دالة عكسية للأخرى، ومثل منحناهما على الشاشة نفسها في الحاسبة البيانية. أوجد (k of )(x)، وماذا تمثل هذه الدالة؟ إذا كانت درجة الحرارة 60°C ، فأوجد درجة الحرارة المطلقة المقابلة لها. ضع قيودًا على مجال كل دالة من الدوال الآتية حتى تصبح دالة متباينة. ثم أوجد الدالة العكسية لها : -4≥ x (48 (49 49 -4 < X -5≥x -5 < x ' f(x) = { f(x) = { x2 -2x+5 -4x + 6 2x - 8 ' (50) اتصالات أعلنت شركة لبيع أجهزة الهاتف المحمول عن عرض مبين في الشكل أدناه. فكانت الشركة تخصم 50 ريالًا وتمنح تخفيضا مقداره %10 من سعر الجهاز الأصلي. مركز بيع الهاتف النقال 10% تخفيضات على سعر كل هاتف 50 ريالا خصم عند البيع | f(x) = 2 - | x + 9 | 41 4ty (40 y 12 -16 -8 Ox 8 4 -8 -12 X (39 (41 4 12 | f(x) = (x - (5) 2 y (42 y 8 -8 4 -8 -40 4 8x X | f(x) = x2 - 6 8. + -12 |f(x) = | x + 5 | − 4| (43) أزهار تحتاج فاطمة إلى 75 زهرة لتزيين قاعة في إحدى المناسبات، فإذا كان بإمكانها شراء قرنفل بسعر 3 ريالات للزهرة الواحدة وشراء جوري بسعر 5 ريالات للزهرة الواحدة، فأجب عما يأتي: a اكتب دالة تمثل التكلفة الكلية لشراء الأزهار. أوجد الدالة العكسية لدالة التكلفة. وماذا يمثل كل متغير فيها ؟ حدّد مجال دالة التكلفة ومجال الدالة العكسية لها. إذا كانت التكلفة الكلية لشراء الأزهار 305 ريالات، فكم زهرة من القرنفل اشترت؟ a اكتب دالة " لسعر الجهاز بدلالة سعره الأصلي إذا تم خصم 50 ريالًا فقط. اكتب دالة d لسعر الجهاز بدلالة سعره الأصلي إذا تم منح التخفيض (%10) فقط. اكتب قاعدة تمثل T = rod إذا تم التخفيض ثم الخصم. d أوجد 1- T ، وماذا تمثل ؟ إذا كانت التكلفة الكلية لشراء جهاز بعد التخفيض ثم الخصم 760 ريالا، فكم يكون سعره الأصلي؟ إذا كانت 6 + 2 = f(x) = 8x - x فأوجد: 4, g(x) 2x (f-1 og−1)(x) (51 - (8-1 of 1) (x) (52 (fog)-1(x) (53 (g of) -1 (x) (54 وزارة التعليم Ministry of Education 2024-1446 الفصل 1 تحليل الدوال 70

(55) تمثيلات متعددة: تمثيلات متعددة سوف تستقصي في هذه المسألة وجود أو عدم وجود دالة عكسية لكل من الدالة الزوجية والدالة الفردية. a بيانيا : مثل بيانيًا منحنيات ثلاث دوال زوجية مختلفة. هل تحقق هذه الدوال اختبار الخط الأفقي؟ : : (b تحليليًّا كون تخمينا حول وجود أو عدم وجود دالة عكسية للدالة الزوجية. أثبت صحة تخمينك بالطريقة الجبرية أو انفه. بيانيا : مثل بيانيًا منحنيات ثلاث دوال فردية مختلفة. هل تحقق هذه الدوال اختبار الخط الأفقي؟ d تحليليا كون تخمينا حول وجود أو عدم وجود دالة عكسية للدالة الفردية. أثبت صحة تخمينك بالطريقة الجبرية أو انفه. مسائل مهارات التفكير العليا 56 تبرير إذا كان للدالة أصفرًا عند 6، ولها دالة عكسية ، فما الذي يمكنك معرفته عن منحنى الدالة 1-f؟ (57) اكتب وضح القيود التي يجب وضعها على مجال الدالة التربيعية ليكون لها دالة عكسية. وضّح بمثال. 58) تبرير هل العبارة الآتية صحيحة أم خاطئة. برّر إجابتك. " يوجد دالة عكسية لكل دالة خطية * 66 (59) تحد : إذا كانت 3 = (23) f(x) = x 3 - a, f1 ، فأوجد قيمة a . 60 تبرير هل توجد دالة (f(x تحقق اختبار الخط الأفقي، وتحقق المعادلتين 0 = (lim f(x) = (0, lim f(x في الوقت نفسه؟ 00 - X X-X f(x) = x3 (64 y = | x3 + 3 | (a y = -(2x)³ (b y = 0.75(x + 1)³ (c f(x) = |x| (65 y= |2x| (a y= |x-5 (b y = |3x + 1| - 4 (c أوجد متوسط معدل التغير لكل دالة فيما يأتي في الفترة المعطاة: (الدرس 4-1) f(x) = x3 - x, [0 3] (66 f(x) = x 4 - 2x + 1, [51] (67 تدريب على اختبار 3x (68) أي الدوال الآتية تمثل الدالة العكسية للدالة 5 -3 = (f(x ؟ 2x + 5 3 A g(x) = g(x) 3x + 5 2 g(x)=2x+5 C B = 2 8(x): = 2x-5 D 3 مراجعة تراكمية لكل زوج من الدوال الآتية، أوجد f o g ، ثم أوجد مجال دالة التركيب (الدرس 6-1 f(x) = x2 - 9 (61 g(x) = x+4 f(x) = 11x- 7 (62 2 g(x) = x+6 (69) إذا كان كل من n و n عددًا صحيحًا فرديًا، فأي العبارات الآتية صحيحة ؟ (I 12 + m2 عدد زوجي m2 + n2 (II يقبل القسمة على 4 m + n)2 (III يقبل القسمة على 4 A B C كلها غير صحيحة I فقط I و II فقط صحیحتان I D و III فقط صحیحتان وزارة التعليم الدرس 7-1- العلاقات والدوال العكسية 71 Min 2024-1446 استعمل منحني الدالة الرئيسة (الأم) المعطاة لوصف منحنى كل دالة مرتبطة بها لكل مما يأتي: (الدرس 5-1) f(x) = x2 (63 y = (0.2x)² (a y = (x-5)²-2 (b y = 3x² + 6 (c

الفصل 1 دليل الدراسة و المراجعة ملخص الفصل مفاهيم أساسية الدوال (الدرس 1-1) المجموعات الجزئية الشائعة من مجموعة الأعداد الحقيقية هي الأعداد النسبية الأعداد غير النسبية، الأعداد الصحيحة الأعداد الكلية، الأعداد الطبيعية. • الدالة هي علاقة تربط كل عنصر فى مجالها بعنصر واحد فقط في مداها. • يحقق منحنى أي دالة اختبار الخط الرأسي. تحليل التمثيلات البيانية للدوال والعلاقات (الدرس (2-1) . قد تكون المنحنيات متماثلةً حول المحور y ، أو المحور x ، أو نقطة الأصل. • الدالة الزوجية متماثلة حول المحور ل ، والدالة الفردية متماثلة حول نقطة الأصل. الاتصال وسلوك طرفي التمثيل البياني والنهايات (الدرس (3-1) . إذا كانت قيم الدالة ( f ( x تقترب من قيمة واحدة L عندما تقترب x من C من الجهتين، فنقول: إن نهاية (f(x عندما تقترب x من تساوي L . وتكتب lim f(x) = L . X-C المفردات الصفة المميزة للمجموعة (ص. 8) الثابتة (ص 36) رمز الفترة (ص. 9) الدالة (ص. 9) رمز الدالة (ص. 11) المتغير المستقل (ص. 11) المتغير التابع (ص. 11) الدالة متعددة التعريف (ص. 12) الأصفار (ص. 18) الجذور (ص. 18) النقطة الحرجة (ص. 38) العظمى (ص. 38) الصغرى (ص. 38) القصوى (ص. 38) متوسط معدل التغير (ص. 40) القاطع (ص. 40) الدالة الرئيسة (الأم) (ص. 46) الدالة الثابتة (ص. 46) الدالة المحايدة (ص. 46) الدالة التربيعية (ص. 46) الدالة التكعيبية (ص 46) دالة الجذر التربيعي (ص. 46) دالة المقلوب (ص. 46) دالة القيمة المطلقة (ص. 47) التماثل حول مستقيم (ص. 19) التماثل حول نقطة (ص. 19) الدالة الزوجية (ص. 21) الدالة الفردية (ص. 21) الدالة المتصلة (ص. 26) النهاية (ص. (26) الدالة غير المتصلة (ص. 26) الدالة الدرجية (ص. 47) عدم الاتصال اللانهائي (ص. 26) دالة أكبر عدد صحيح (ص. 47) عدم الاتصال القفزي (ص. (26) قد تكون الدالة غير متصلة، ونوع عدم الاتصال هو لانهائي، أو عدم الاتصال القابل للإزالة (ص. 26) قفزي، أو قابل للإزالة. القيم القصوى ومتوسط معدل التغير (الدرس 14 عدم الاتصال غير قابل للإزالة (ص. 29) تكون الدالة إما متزايدةً أو متناقصةً أو ثابتة على فترات معينة. . تتضمن القيم القصوى القيمة العظمى المحلية والصغرى المحلية، والعظمى المطلقة، والصغرى المطلقة. • يعطى متوسط معدل التغير بين نقطتين بالقاعدة m sec f(x2) − f(x1) x2-x1 ( الدرس 5-1) الدالة الرئيسة (الأم) والتحويلات الهندسية تتضمن التحويلات الهندسية على الدالة الرئيسة (الأم) الانسحاب الانعكاس التمدد العمليات على الدوال وتركيب دالتين (الدرس 6-1 : إن حاصل جمع، وطرح وضرب، وقسمة، وتركيب أي دالتين ينتج دوال جديدة . العلاقات والدوال العكسية (الدرس (17) سلوك طرفي التمثيل البياني (ص. 30) المتزايدة (ص 36) المتناقصة (ص. 36) اختبر مفرداتك التحويل الهندسي (ص. 47) الانسحاب (ص. 48) الانعكاس (ص. 48) التمدد (ص. 50) تركيب دالتين (ص. 57) العلاقة العكسية (ص. 64) الدالة العكسية (ص. 64) الدالة المتباينة (ص. 65) حدد ما إذا كانت كل جملة مما يأتي صحيحة أو غير صحيحة، وإذا كانت غير صحيحة، فاستبدل المفردة التي تحتها خط حتى تصبح صحيحة. مداها. (1) تعين الدالة لكل عنصر في مجالها عنصرًا واحدًا فقط في (2) المنحنيات المتماثلة حول نقطة يمكن تدويرها °180 حول النقطة، فتبدو كأنها لم تتغير. 3 للدالة الفردية نقطة تماثل. 4) لا يتضمن منحنى الدالة المتصلة فجوةً أو انقطاعًا. (5) الدالة الفردية متماثلة حول المحور y . • تكون كلٌّ من العلاقتين AB عكسية للأخرى إذا وفقط إذا 6) الدالة (f(x التي تتناقص قيمها مع تزايد قيم x تسمى دالةً متناقصةً. وجد (ba) في إحداهما فإنه يوجد (ab) في الأخرى. (7) تتضمن القيم القصوى لدالة قيمًا عظمى محليةً أو صغرى محليةً. تكون كلٌّ من الدالتين -1 f, f, عكسية للأخرى إذا وفقط إذا (8) انسحاب المنحنى عبارة عن صورة مرآة للمنحنى الأصلي حول مستقيم. كان f [f -1 (x)] = x, f - [ f(x)] = x . 9) تحقق الدالة المتباينة اختبار الخط الأفقي. (10) الدالة المتباينة لها محور تماثل. 72 الفصل 1 تحليل الدوال وزارة التعليم Ministry of Education 2024-1446

المفاهيم الأساسية
ملخص الدروس الدوال الصفحات 8 - 15 ) 1-1 في كل علاقة مما يأتي، حدد ما إذا كانت y دالة في x أم لا: مثال 1 في العلاقة y2 - 8 = x حدد ما إذا كانت y تمثل دالة في x أم لا: حل بالنسبة إلى y. y3 - x = 4 (12 3x - 2y = 18 (11 (14 (13 x LO 5 7 7 9 x 9 11 11 13 y إذا كانت 4 + f(x) = x2 - 3x ، فأوجد كلا من القيمتين الآتيتين: f(5) (15 - f(-3x) (16 أوجد مجال كل دالة من الدوال الآتية: y² - 8 = x y2 = x + 8 y = ±Vx + 8 الدالة الأصلية أضف 8 للطرفين خذ الجذر التربيعي للطرفين في هذه العلاقة، لا لا تمثل دالة في المتغير x ؛ لأن كل قيمة لـ x أكبر من y 8- ترتبط بقيمتين من قيم . مثال 2 إذا كانت 6 - x) = - 3x2 + x) ، فأوجد (2). عوض 2 مكان x في العبارة: 6 – 3x2 + x- x=2 بسط g(2)=-3(2)²+2-6 =-12+26=-16 g(x) = √√√6x − 3 (18 f(x) = 5x² - 17x +1 (17 - X v(x): = (20 x2 ― h(a) = : 5 (19 a +5 1-2 تحليل التمثيلات البيانية للدوال والعلاقات الصفحات 16 - 25 الصفح استعمل التمثيل البياني لإيجاد مجال كل دالة ومداها في كل مما يأتي: (21 y 4 1 -4 O 4 8x -4 -8- (22 18 y 0 مثال 3 استعمل التمثيل البياني للدالة f(x) = x3 - 8x2 + 12x لإيجاد مقطعها y وأصفارها . ثم أوجد هذه القيم جبريًّا. التقدير بيانيا : يتضح من الشكل أن منحنى (f(x يقطع المحور ( عند (0) ؛ لذا فإن المقطع ل هو 0 . المقاطع x (أصفار الدالة) تبدو قريبةً من | f(x) = x3 - 8x2 + 12x 1619 8 -4 O 4 8x -16 .0,2,6 الحل جبريًا : لإيجاد المقطع y، أوجد (0)f. f(0) = 0³ 8.02 +12.0=0 حلل المعادلة المرتبطة بالدالة إلى العوامل x لإيجاد أصفار الدالة. 0 = x(x2 - 8x + 12) = x (x-2) (x — 6) .0,2,6 أصفار الدالة هي . f . وزارت التعليم الفصل 1 دليل الدراسة والمراجعة M73 of E 2024-1446 أوجد المقطع لا ، والأصفار لكل دالة مما يأتي: f(x) = x2 - 6x - 27 (24) f(x) = Vx + 2 - 1 (26 f(x) = 4x - 9 (23 f(x) = x3 - 16x (25)

حدد ما إذا كانت y تمثل دالة x أم لا:
أوجد g(2) .
استعمل التمثيل البياني للدالة لإيجاد مقطعها y وأصفارها. ثم أوجد القيم جبريا.
دليل الدراسة و المراجعة الفصل 1 1-3 الاتصال والنهايات الصفحات (3526 حدد ما إذا كانت كل دالة مما يأتي متصلة عند قيم x المعطاة. وبرر إجابتك باستعمال اختبار الاتصال. وإذا كانت الدالة غير متصلة فبين نوع عدم الاتصال لانهائي، قفزي، قابل للإزالة. مثال 4 == 1 x-4 حدد ما إذا كانت الدالة : (f(x متصلة عند 4 = x = 0, x . وبرر إجابتك باستعمال اختبار الاتصال. وإذا كانت الدالة غير متصلة فحدد نوع عدم الاتصال لانهائي، قفزي، قابل للإزالة. 0.25- = (0)f ، لذلك f معرفة عند 0 . وتقترب : الدالة من -0.25 عندما تقترب x من 0 . x -0.1 -0.01 0 0.01 0.1 f(x) -0.249 -0.244 -0.25 -0.251 -0.256 f(x) = x2 - 3x, x = 4 (27 f(x) = √2x - 4, x = 10 (28 f(x) = x = 0, x = 7 (29) x+7,x=0,x=7 X f(x) = 2, x = 2, x=4 (30 f(x) = { 3 {3x X 1 ― ' 4 x<1 2x, x> 1 , x = 1 (31 بما أن 0.25 = (0)lim f(x) = - 0.25, f فإن (f(x متصلة عند 0 = x . x-0 بما أن أ غير معرفة عند 4 = x فإن أ غير متصلة عند 4 وهو استعمل التمثيل البياني لكل من الدالتين الآتيتين لوصف سلوك طرفي عدم اتصال لا نهائي. التمثيل البياني لكل منهما : (32 8x ہے 8 -4 D (33 4 8x مثال 5 استعمل التمثيل البياني للدالة: = -2x4 - 5x + 1 f(x) = -2x4 5x+1 لوصف سلوك طرفي التمثيل البياني. 4 8x y ١٥ پنے -8 -4 8. نه -12- اختبر منحنی (f(x . -8 عندما x ، فإن - → (f(x → عندما x - - o ، فإن 0 (f(x →> القيم القصوى ومتوسط معدل التغير ( الصفحات 36 - 44 مثال 6 1-4 استعمل التمثيل البياني لكل من الدالتين الآتيتين لتقدير الفترات إلى أقرب 0.5 وحدة التي تكون فيها الدالة متزايدة أو متناقصة أو ثابتة. ثم استعمل التمثيل البياني للدالة f(x) = x3 - 4x لتقدير الفترات إلى قدر إلى أقرب 0.5 وحدة القيم القصوى للدالة، وبين نوعها. أقرب 0.5 وحدة التي تكون فيها الدالة متزايدة أو متناقصة أو ثابتة. ثم قدر إلى أقرب 0.5 وحدة القيم القصوى للدالة، وبين نوعها. وزارة التعليم Ministry of Education 2024-1446 8 y A -40 -4- -8 8x 4 الدالة متزايدة في الفترة (1) ، ومتناقصة في الفترة (11) ، ومتزايدة في الفترة (1) . 84 4 (35 y -4 -20 2 4X 0 x (34 -8 أوجد متوسط معدل التغير لكل من الدالتين الآتيتين في الفترة المعطاة: للدالة قيمة عظمى محلية عند (13) ، وقيمة صغرى محلية عند (13) . f(x) = x3 + 3 x + 1, [0, 2] (36 f(x) = x² + 2x + 5, [-5,3] (37 الفصل 1 تحليل الدوال 74

حدد ما إذا كانت الدالة متصلة عند x=0, x=4 وبرر إجابتك باستعمال اختبار الاتصال.
مثال5- استعمل التمثيل البياني لوصف سلوك طرفي التمثيل البياني
مثال 6
27- حدد ما اذا كانت كل دالة مما ياتي متصلة عند قيم x المعطاة، وبرر إجابتك باستعمال اختبار الاتصال . وإذا كانت الدالة غير متصلة فبين نوع عدم الاتصال لا نهائي، قفزي، قابل للإزالة.

1-5 الدوال الرئيسة (الأم) والتحويلات الهندسية ( الصفحات 46 - 55) مثال 7 أوجد الدالة الرئيسة (الأم) (f(x) للدالة 7 + |3 - g(x) = - x ، وصف العلاقة بين منحنيي الدالتين، ثم مثْلهما في مستوى إحداثي واحد. أوجد الدالة الرئيسة (الأم) (f(x للدالة (g(x في كل مما يأتي، وَصِف العلاقة بين منحنيي الدالتين، ثم مثلهما في مستوى إحداثي واحد. (x6)2-5 (39 g(x) = == g(x)=√√x-3+2 (38 g(x) = [x] + 3 (41 1 g(x) = (40 2(x+7) الدالة الرئيسة (الأم) لـ (x) | f(x) = |x . ينتج منحنى هي الدالة 8 من منحنى الدالة f بانعكاس حول المحور x ، صف العلاقة بين الدالتين (f(x) = V ,(x في كل مما يأتي، ثم اكتب معادلة الدالة (x) . وانسحاب مقداره 3 وحدات إلى اليمين، وانسحاب مقداره (42 (43 y 7 وحدات إلى أعلى. 4 8x g(x) = x - 3|+7 |f(x) = |x|| 84 4 -8 140 + -8 مثال 8 | of y = g(x) X |y = g(x) 0 x العمليات على الدوال وتركيب دالتين ( الصفحات 56 - 63 1-6 إذا كانت 7 + f(x) = x3 - 1 = x ، فأوجد () () () • x), (f - gx), f)( + ) ، ثم اكتب مجال الدالة الناتجة. (f + g)(x) = f(x) + g(x) = (x³ 1) + (x+7) x3 - = x + x + 6 Spilul is JSJ (ƒ + g)(x), (ƒ — g)(x), (ƒ • g)(x), (§) (x) \. من (f(x) (x فيما يأتي. ثم اكتب مجال الدالة الناتجة. f(x) = 4x2 - 1 (45 g(x) = 5x – 1 1 f(x) = x + 3 g(x) = 2x2 + 4x 6 - (44 f(x) = x³ - 2x² +5 (46 x3 f(x) = (47 8(x) = 1/27 g(x) = 4x2 - 3 x2 وزارة التعليم أوجد (2)[fox), g of (x), f o g] لكل دالتين من الدوال الآتية: =4x-11, g(x) = 2x² - 8 (48 f(x) = f(x) = x² + 2x + 8, g(x) = x − 5 (49 - f(x) = x² - 3x + 4, g(x) = x² (50 مجال (f(x) هو {x | x E R}. (f − g)(x) = f(x) − g(x) = (x31)(x+7) = x3 - x - 8 مجال (f - (x) هو {x | x E R}. (f• g)(x) = f(x) • g(x) = (x3 - 1)(x + 7) = x4 + 7x3 - x 7 اكتب مجال f o g متضمناً أية قيود إذا لزم، ثم أوجد f o g . مجال (x) (۰) هو xx . ( 2 ) (x) = f(x) = x³ - 1 g(x) x3 x+7 f(x) = Vx - 2 (52) g(x) = 6x - 7 مجال (x) هو {x | x + 7, x e R . R} الفصل 1 دليل الدراسة والمراجعة M75 of E 2024-1446 f(x) = 1 (51 X 3 g(x) = 2x-6

مثال 7: أوجد الدالة الرئيسة (الام) للدالة +7 g(x)=-|x-3| وصف العلاقة بين منحنيي الدالتين، ثم مثلها في مستوى إحداثي واحد.
مثال 8: أوجد (x)(f+g) لكل من الدالتين f(x), g(x) فيما ياتي، ثم أكتب مجال الدالة الناتجة.
الفصل 1 دليل الدراسة والمراجعة 1-7 العلاقات والدوال العكسية ( الصفحات 64 - 71) مثال 9 أوجد الدالة العكسية في كل مما يأتي، إن أمكن، ثم مثل 1-f, f في أوجد الدالة العكسية للدالة 9 - y = x3 مستوى إحداثي واحد. = -4x+8 (54 y = 2x (53 y = 1/1 X - 3 (56 y = 2 x + 3 (55) . بدل مكاني x y لتحصل على المعادلة 9 - 3 = x ، ثم حل بالنسبة إلى y . مثل كل دالة من الدوال الآتية باستعمال الحاسبة البيانية، واختبر ما إذا كان المعكوس يمثل دالةً أم لا. f(x) = x3 f(x) = x3 - 4x2 (60) (58 f(x) = |x| +6 (57 f(x) = 3 (59 x + 6 x = y3 - 9 x + 9 = y3 √√x+9 = y أي أن الدالة العكسية هي . y = Vx + 9 تطبيقات ومسائل (61) الهواتف المحمولة : قدمت إحدى شركات الاتصالات عرضًا 64 كرة قدم يبين الجدول أدناه عدد الأهداف التي سجلها لاعب في على الهواتف المحمولة بحيث يدفع المشترك 40 ريالًا في الشهر. ويتضمن ذلك 500 دقيقة مكالمات نهارية مجانية كحد أقصى خلال الشهر، ويدفع 0.2 ريال عن كل دقيقة نهارية تزيد على 500 دقيقة. (الدرس 1-1) ) اكتب الدالة (x)) للتكلفة الشهرية لإجراء مكالمات نهارية مدتها دقيقة. كم سيدفع مشترك إذا أجرى مكالمات نهارية مدتها 450 دقيقةً، 550 دقيقة ؟ مثل الدالة (p(x بيانيا. خمسة مواسم كروية (الدرس 4-1) السنة عدد الأهداف (a 1437 1436 42 42 1435 23 1434 36 1433 5 وضح لماذا يمثل عدد الأهداف عام 1435 هـ قيمةً صغرى محلية. إذا كان متوسط معدل التغير لعدد الأهداف بين عامي 1437 و 1440هـ يساوي 5 أهداف لكل عام. فكم هدفا سجل اللاعب عام 1440 هـ ؟ 62 أعمال يبين التمثيل البياني أدناه الدخل الذي حققه متجر صغير في 65 فيزياء: رمي حجر أفقيا من على حافة جرف، وكان مقدار سرعته الفترة من عام 1434 هـ إلى 1440 هـ (الدرس (2-1) الدخل بعشرات آلاف الريالات 340 335 30 25 20 15 10 5 1 2 3 4 5 6 7 السنوات منذ 1434 هـ قدر دخل المتجر سنة 1437 هـ قدر السنة التي حقق فيها المتجر دخلًا مقداره 100000 ريال. 63 رواتب بعد 5 سنوات من عمل وليد في إحدى الشركات تقاضى زيادة على راتبه مقدارها 1500 ريال شهريا. هل الدالة التي تمثل راتب وليد متصلة أم غير متصلة ؟ برّر إجابتك (الدرس (3-1) معطى بالدالة : 49 + 9.82) = ) . حيث t الزمن بالثواني، (t) السرعة بالمتر لكل ثانية مثل بيانيًّا دالة السرعة خلال أول 6 ثوان من رمي الحجر الدرس (15) 10% (66) ثقافة مالية : إذا كان ثمن شريحة الإنترنت 500 ريال. وقدمت إحدى الشركات العرض التالي: خصم من ثمن الشريحة و 20 ريالًا عند تفعيلها . كم سيكون ثمن الشريحة بعد تفعيلها. (الدرس 6-1 (67) قياس تذكر أن 1 بوصةً تساوي 2.54 سم تقريبا (الدرس (17) ) اكتب دالة (Ax لتحويل مساحة مستطيل من البوصات المربعة إلى السنتمترات المربعة. أوجد (A -1 (x لتحويل مساحة مستطيل من السنتمترات المربعة إلى البوصات المربعة. 76 الفصل 1 تحليل الدوال وزارة التعليم Ministry of Education 2024-1446

مثال 9: أوجد الدالة العكسية للدالة:
الفصل 1 اختبار الفصل في كل علاقة مما يأتي، حدد ما إذا كانت y تمثل دالة في x: x = y2 - 5 (1 y = Vx2 + 3 (3 (2 y استعمل منحنى كل من الدالتين الآتيتين لتقدير الفترات التي تكون عندها الدالة متزايدة أو متناقصة إلى أقرب 0.5 وحدة. (14 (15 y x -8 -40 O X 0+ -4 8 8x 4 (4 موقف سيارات يتقاضى موقف للسيارات مبلغ 3 ريالات مقابل كل ساعة أو جزء من الساعة لأول ثلاث ساعات، فإذا زادت المدة عن الثلاث ساعات، فإنه يتقاضى 15 ريالًا عن المدة كلها . ( اكتب دالة (x) تمثل تكلفة وقوف سيارة مدة x من الساعات. b) أوجد (2.5) عيّن مجال الدالة (x)، وبرر إجابتك. حدد مجال كل دالة من الدالتين الممثلتين أدناه ومداها: 16 استعمل التمثيل البياني للدالة في السؤال 14 أعلاه، وقدر قيمة x التي يكون للدالة عندها قيمة قصوى مقربة إلى أقرب 0.5 وحدة، وبين نوعها. (17) اختيار من متعدد : أي الدوال الآتية يمثلها التمثيل البياني المجاور؟ y 8 + -8 -40 4 8x -8. f(x) = |x − 4| − 3 A - f(x) = |x − 4| +3 B f(x) = |x + 4| − 3 C - f(x) = |x + 4| +3 D y 8 حر -8-4 O -4 (6 y 8 4- ہے 4 8x -8 -40 4 Tool 8x (5 أوجد المقطع y والأصفار لكل دالة من الدالتين الآتيتين: -8 f(x) = x3 + 4x2 + 3x (8 f(x) = 4x2 - 8x - 12 (7 (9) اختيار من متعدد: أي العلاقات الآتية متماثلة حول المحور x ؟ -x2 - yx = 2 A x3y = 8 B y= |x| C -y2 = -4x D حدد ما إذا كانت كل من الدالتين الآتيتين متصلة عند 3 = x ، وإذا كانت غير متصلة، فحدد نوع عدم الاتصال لا نهائي قفزي قابل للإزالة. x - و } = (f(x { 9 2x x < 3 x ≥ 3 (10 f(x) = x -3 (11 2 _ 9 x2 . أوجد متوسط معدل التغير لكل دالة من الدالتين الآتيتين في الفترة [2] f(x) = -x4 + 3x (12 f(x) = Vx + 3 (13) 18 عين الدالة الرئيسة (الأم) (f(x للدالة 3 (3 + x) = - ( x)، ثم مثل الدالة (x) بيانيا. إذا كانت 6 - x) = x2 - 36, f(x) = x) ، فأوجد كل دالة من الدالتين الآتيتين، ثم أوجد مجالها. () (x) (19 [g of](x) (20 21 درجة الحرارة تستعمل معظم دول العالم الدرجات السيليزية C لقياس درجة الحرارة والمعادلة التي تربط بين درجات الحرارة . 9 السيليزية C والفهرنهايتية F هي 32 + C = .F a اكتب كدالة بالنسبة إلى F . أوجد دالتين f و 8 بحيث يكون (C = [fo (F . بين ما إذا كان للدالة دالة عكسية أم لا في كل مما يأتي، أوجدها في حالة وجودها، وحدّد أية قيود على مجالها. x + 3 x-8 f(x) = (23 f(x) = (x - 23 (22) f(x) = x2 – 16 (25) f(x) = V4 - x (24) وزارة التعليم الفصل 1 اختبار الفصل 77 Min 2024-1446

استعمل منحنى كلا من الدالتين الاتيتين لتقدير الفترات التي تكون عندها الدالة متزايدة أو متناقصة إلى أقرب 0.5 وحدة.





 0
0 

 0
0 
 0
0