تمييز متوازي الأضلاع - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
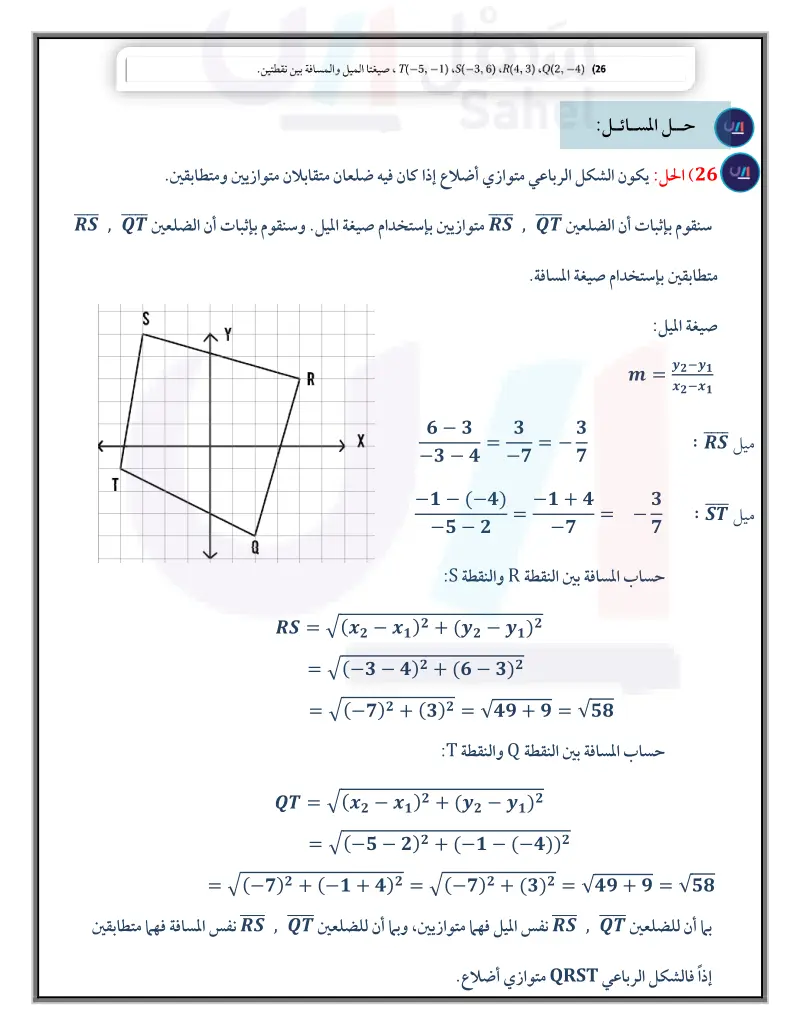
رابط الدرس : www.ien.edu.sa تمييز متوازي الأضلاع Distinguishing Parallelogram 5-3 فيما سبق درست خصائص متوازي الأضلاع وطبقتها. (الدرس (2-5) والآن : ا أتعرف الشروط التي تؤكد أن شكلا لماذا؟ قصت فاطمة شرائح ورقية ملونة لتكون خلفية للوحة الرياضيات عند مدخل المدرسة. فسألتها صديقتها: كيف قصصت الشرائح دون استعمال المنقلة بحيث كان الضلعان العلوي والسفلي في كل منها متوازيين ؟ لوحة الرياضيات أجابت فاطمة : بما أن الضلعين الأيمن والأيسر للشريحة متوازيان، فإننا نحتاج فقط التأكد رباعيا متوازي أضلاع من أن لهما الطول نفسه عند قص الضلعين العلوي والسفلي للشريحة حتى نضمن أن وأطبقها. - أبرهن على أن أربع نقاط في المستوى الشرائح سوف تشكل متوازيات أضلاع. شروط متوازي الأضلاع في الشكل الرباعي، إذا كان كل ضلعين متقابلين متوازيين الإحداثي تشكل رؤوس فإنه متوازي أضلاع بحسب التعريف. ولكن ليس هذا هو الشرط الوحيد الذي يمكن استعماله لتحديد ما إذا كان الشكل الرباعي متوازي أضلاع. متوازي أضلاع نظريات شروط متوازي الأضلاع 5.9 في الشكل الرباعي، إذا كان كل ضلعين متقابلين متطابقين فإن الشكل الرباعي متوازي أضلاع مثال : إذا كان AB = DC, AD = BC فإن ABCD متوازي أضلاع 5.10 في الشكل الرباعي إذا كانت كل زاويتين متقابلتين متطابقتين فإن الشكل الرباعي متوازي أضلاع مثال : إذا كانت A = B = LD ، فإن ABCD متوازي أضلاع 5.11 إذا كان قطرا شكل رباعي ينصف كل منهما الآخر، فإن الشكل الرباعي متوازي أضلاع مثال : إذا كان ACB ينصف كل منهما الآخر، فإن ABCD متوازي أضلاع 5.12 في الشكل الرباعي إذا كان فيه ضلعان متقابلان متوازيين ومتطابقين، فإن الشكل الرباعي متوازي أضلاع مثال : إذا كان AB || DC, AB = DC ، فإن ABCD متوازي أضلاع 3 ft 3 ft أضف إلى مطويتك A B # C A B A B C A B + سوف تبرهن النظريتين 5.11 5.10 في السؤالين 2931 على الترتيب وتبرهن النظرية 5.12 في مثال 5 D الدرس - تمييز متوازي الأضلاع ال157يم Ministry of Educat 2024-1446

J W X Y نظرية 5.9 برهان اكتب برهاناً حرا للنظرية 5.9 المعطيات WX=ZY, WZ = XY المطلوب: WXYZ متوازي أضلاع. البرهان ارسم قطعة مستقيمة مساعدة ZX (قطر WXYZ) لتشكيل AZWX, AXYZ. ومن المعطيات WX = ZY, WZ = XY . وكذلك ZX = XZ بحسب خاصية الانعكاس للتطابق؛ إذن = AZWX AXYZ بحسب SSS . وبما أن العناصر المتناظرة في المثلثين المتطابقين تكون متطابقة، فإن WXZ ZX, LWZX = LYXZ . وهذا يعني أن W X Y Z | X بحسب عكس نظرية الزاويتين المتبادلتين داخليا. وبما أن الأضلاع المتقابلة في WXYZ متوازية، فإنه متوازي أضلاع بـ بحسب التعريف. F 14 in. G 80 100° 14 in. H مثال 1 تحديد متوازي الأضلاع حدد ما إذا كانت المعطيات على الشكل الرباعي المجاور كافية ليكون متوازي أضلاع أم لا. برّر إجابتك. الضلعان المتقابلان FG JH متطابقان؛ لأنهما متساويان في الطول. وبما أن FGH GH متحالفتان و متكاملتان، فإن FG || JH . إذن فمن النظرية 5.12، يكون FGHJ متوازي أضلاع (18) 115° 65 5 cm تحقق من فهمك 12 cm (1A 5 cm 12 cm الربط مع الحياة يضع الفنيون أدواتهم في صناديق ذات طبقات متداخلة تسهل تنظيم الأدوات وتبقيها في متناول أيديهم. يمكنك استعمال شروط متوازي الأضلاع لإثبات علاقات من واقع الحياة. مثال 2 من واقع الحياة استعمال متوازي الأضلاع لإثبات علاقات صندوق الأدوات في الشكل المجاور، إذا كان PQ = RS, PR = QS ، فبين لماذا تبقى الطبقتان العلوية والوسطى متوازيتين عند أي ارتفاع . بما أن كل ضلعين متقابلين في الشكل الرباعي PQSR متطابقان، فإن PQSR متوازي أضلاع بحسب النظرية 5.9. إذن P || RS ؛ لذا وبغض النظر عن ارتفاع الطبقتين فستبقيان متوازيتين P ° R S تحقق من فهمك 2) لوحات عُد إلى فقرة "لماذا؟" بداية الدرس، وضح لماذا يكون خطي القص أعلى وأسفل كل شريحة متوازيين. الفصل 5 الأشكال الرباعية وزارة التعليم Ministry of Education 2024-1446 158

يضع الفنيون أدواتهم في صناديق ذات طبقات متداخلة تسهل تنظيم الأدوات وتبقيها في متناول أيديهم
تنبيه ! متوازي الأضلاع في المثال 3 إذا كانت تساوي 4 فإن ا يجب أن تساوي 2.5 حتى يمكنك استعمال الجبر مع شروط متوازي الأضلاع لإيجاد القيم المجهولة التي تجعل شكلًا رباعيا متوازي أضلاع. مثال 3 استعمال متوازي الأضلاع لإيجاد القيم المجهولة في الشكل المجاور : 3 + 4 = FK = 3x - 1, KG، يكون الشكل الرباعي 3 + JK = 66 - KH = 2x . أوجد قيمتي x, y بحيث يكون FGHJ متوازي أضلاع وهذا يعني أنه إذا كانت تساوي 4 و لا تساوي مثلا فلن يكون FGHJ متوازي أضلاع الشكل الرباعي FGHJ متوازي أضلاع بناءً على النظرية 5.11، إذا كان قطرا شكل رباعي ينصف كل منهما الآخر، فإن الشكل الرباعي متوازي أضلاع؛ لذا أوجد قيمة x التي تجعل FK = KH ؛ وقيمة y التي تجعل JK = KG . FK = KH 3x - 1 = 2x + 3 x-1 = 3 x = 4 JK = KG 6y - 2 = 4y + 3 2y-2=3 2y= 5 تعريف تطابق القطع المستقيمة بالتعويض بطرح 2 من كلا الطرفين بإضافة 1 إلى كلا الطرفين تعريف تطابق القطع المستقيمة بالتعويض بطرح 4 من كلا الطرفين بإضافة 2 إلى كلا الطرفين G H F K بقسمة كلا الطرفين على 2 y= 2.5 إذن عندما تكون 2.5 = 4 = x ، يكون الشكل الرباعي FGHI متوازي أضلاع. تحقق من فهمك أوجد قيمتي x, y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع. 4y-9 3x+4 5x 2 2y+5 (3B 56° (5y-26)° (4y+4)° 7x (3A تعرفت شروط متوازي الأضلاع، وفيما يأتي ملخّص يوضح كيفية استعمال هذه الشروط لإثبات أن شكلًا رباعيا يمثل متوازي أضلاع. | ملخص المفهوم إثبات أن شكلا رباعيا يمثل متوازي أضلاع يكون الشكل الرباعي متوازي أضلاع إذا حقَّق أيًا من الشروط الآتية (1) إذا كان كل ضلعين متقابلين فيه متوازيين (التعريف) (2) إذا كان كل ضلعين متقابلين فيه متطابقين النظرية (5.9) (3) إذا كانت كل زاويتين متقابلتين فيه متطابقتين (النظرية 5.10) (4) إذا كان قطراه ينصف كل منهما الآخر. (النظرية (5.11) (5) إذا كان فيه ضلعان متقابلان متوازيين ومتطابقين النظرية (5.12) أضف إلى مطويتك الدرس - تمييز متوازي الأضلاع ال159يم Ministry of Educo 2024-1446

متوازي الاضلاع
إرشادات للدراسة صيغة نقطة المنتصف : لبيان أن شكلا رباعيا يمثل متوازي أضلاع متوازي الأضلاع في المستوى الإحداثي: يمكننا استعمال صيغ المسافة بين نقطتين والميل ونقطة المنتصف لتحديد ما إذا كان الشكل الرباعي في المستوى الإحداثي متوازي أضلاع أم لا. مثال 4 متوازي الأضلاع والهندسة الإحداثية هندسة إحداثية مثل في المستوى الإحداثي الشكل الرباعي KLMN الذي رؤوسه 3 ,2 ,7)M ,4 ,8) (2) . وحدد ما إذا كان متوازي أضلاع أم لا. برّر إجابتك باستعمال صيغة الميل. يمكنك استعمال صيغة إذا كانت الأضلاع المتقابلة في الشكل الرباعي متوازية فإنه متوازي أضلاع. نقطة المنتصف، فإذا كانت نقطتا المنتصف للقطرين متساويتين فإن القطرين ينصف كل منهما الآخر. میل KL : میل NM : میل KN : میل LM : 4-3 1 8-2 6 -2-(-3) 1 7-1 6 --3--3--6- = 6 == = 6 بما أن الأضلاع المتقابلة لها الميل نفسه، فإن KL ||NM, LM || KN . لذا فالشكل الرباعي KLMN متوازي أضلاع بحسب التعريف. تحقق من فهمك مثل في المستوى الإحداثي الشكل الرباعي الذي أعطيت إحداثيات رؤوسه فيما يأتي. وحدد ما إذا كان متوازي أضلاع أم لا . برر إجابتك باستعمال الطريقة المحددة في السؤال: 4) (10) ,(1 ,6) ,(2 ,8) ,(33) ، صيغة المسافة. F(-2, 4), G(4, 2), H(4, -2), J(-2, -1) (4B K IN درست سابقا، أنه يمكن التعبير عن إحداثيات رؤوس المثلثات بمتغيرات. ثم استعمال صيغ المسافة بين نقطتين والميل ونقطة المنتصف لكتابة براهين إحداثية للنظريات . ويمكن عمل الشيء نفسه مع الأشكال الرباعية. مثال 5 متوازي الأضلاع والبرهان الإحداثي اكتب برهانًا إحداثيا للعبارة الآتية : مراجعة المفردات البرهان الإحداثي هو برهان تُستعمل فيه أشكال في المستوى الإحداثي والجبر لإثبات مفاهيم هندسية. في الشكل الرباعي، إذا كان فيه ضلعان متقابلان متوازيين و متطابقين فإن الشكل الرباعي متوازي أضلاع الخطوة 1: ارسم الشكل الرباعي ABCD في المستوى الإحداثي على أن يكون AB || DC, AB = DC. عين الرأس A عند النقطة (0,0). . افترض أن طول AB يساوي a وحدة فيكون إحداثيا B هما (a). D(b, c) C(b + a, c x OA(0, 0) B(a, 0) بما أن القطع المستقيمة الأفقية متوازية دائمًا، فعيّن نقطتي طرفي DC على أن يكون لهما الإحداثي لا نفسه وليكن . . بما أن المسافة من D إلى C تساوي أيضًا a وحدة، وبفرض أنّ الإحداثي x للنقطة D يساوي b ، يكون 160 الإحداثي x للنقطة C يساوي b + a . الفصل 5 الأشكال الرباعية وزارة التعليم Ministry of Education 2024-1446

الخطوة 2 استعمل الشكل الذي رسمته لكتابة برهان. المعطيات ABCD شكل رباعي فيه AB || DC, AB = DC المطلوب ABCD متوازي أضلاع برهان إحداثي D(b, c) C(b+a, c) OA(0, 0) x B(a, 0) من التعريف يكون الشكل الرباعي متوازي أضلاع إذا كانت أضلاعه المتقابلة متوازية. ومن المعطيات AB || DC. يبقى أن نثبت أن AD || BC. استعمل صيغة الميل. د تاريخ الرياضيات رينيه ديكارت (1596-1650) C-0 6-0-14:AD Je میل BC : c-0 b+a-a b عالم رياضيات فرنسي، وهو وبما أن AD, BC لهما الميل نفسه، فإن AD || BC ؛ لذا فالشكل الرباعي ABCD متوازي أضلاع؛ لأن كل أول من استعمل المستوى الإحداثي . وقيل إنه فكر أولا بربط كل موقع في مستوى مع زوج من الأعداد. إنشاءات هندسية ضلعين متقابلين فيه متوازيان تحقق من فهمك 5) اكتب برهانًا إحداثيا للعبارة الآتية : إذا كان الشكل الرباعي متوازي أضلاع فإن أضلاعه المتقابلة متطابقة. رسم متوازي أضلاع عُلم طولا ضلعين متتاليين فيه. D الخطوة 4: B D الخطوة 3 B D الخطوة 2 : B الخطوة 1: B استعمل المسطرة لرسم AB . ثم اختر نقطة على القوس الذي فوق افتح الفرجار فتحة مساوية لـ استعمل حافة المسطرة لرسم افتح الفرجار، وثبته عند النقطة A A وسمها D. وارسم قوسا فوقها. ثبت الفرجار AB ، وثبته عند النقطة D وارسم قوسًا يقطع القوس المرسوم من .AD, BC, CD عند النقطة B، وبفتحة الفرجار نفسها ارسم قوسًا فوق B. تأكد النقطة B، سم نقطة التقاطع C. المثال 1 حدد ما إذا كان كل شكل رباعي فيما يأتي متوازي أضلاع أم لا. برر إجابتك. (2 5.1 5 5 4.9 (1 المثال 2 3) نجارة صنع نجار درابزينا لدرج يتكوّن من عمودين رأسيين؛ الأول مثبت فوق الدرجة الأولى، والثاني مثبت فوق الدرجة الأخيرة، ويصل بينهما قاطعان خشبيان كما في الشكل المجاور. كيف يمكن للنجار التحقق من أن القاطعين الخشبيين العرضيين متوازيان، وذلك بأقل عدد من مرات القياس، إذا علمت بأن الدرجتين الأولى والأخيرة مستويتان مع الأرض. عمود رأسي عمود رأسي قاطعان عرضيان . الدرس - تمييز متوازي الأضلاع الت161يم Ministry of Educat 2024-1446

صنع نجار درابزينا لدرج يتكون من عمودين رأسيين الأول مثبت فوق الدرجة الأولى والثاني فوق الدرجة الأخيرة ويصل بينهما قاطعان خشبيان كيف يمكن للنجار التحقق من ان القاطعين الخشبين العرضيين متوازيان

رينيه ديكارت
2x+3 المثال 3 جبر: أوجد قيمتي x, y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع. y + 11 3y-5 x+7 (5 (4) (8x-8)° (7y+2)° (6y+16) (6x+14)° المثال 4 هندسة إحداثية مثل في المستوى الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه فيما يأتي. وحدد ما إذا كان متوازي أضلاع أم لا، برّر إجابتك باستعمال الطريقة المحدّدة في السؤال. JA(-2, 4), B(5, 4), C(8, -1), D(-1, -1) (6 all be disW(-5, 4), X(3, 4), (1, -3), Z(-7,-3) (7 المثال 5 اكتب برهانا إحداثيا للعبارة الآتية : إذا كان الشكل الرباعي متوازي أضلاع، فإنّ قطريه ينصف كل منهما الآخر تدرب وحل المسائل المثال 1 حدد ما إذا كانت المعطيات في كل مما يأتي كافية ليكون الشكل الرباعي متوازي أضلاع أم لا. برر إجابتك. 75° (11 (10 (14 (13 105° W M X Z وزارة التعليم Ministry of Education 2024-1446 (4x-8)° (y-8)° 21 (8y - 12) " 2x + 4y 6y + x 7 (9 (12 المثال 2 15 برهان : إذا كان WXYZ متوازي أضلاع، حيث M ، W = X نقطة منتصف WX ، فاكتب برهانا حرا لإثبات أن AZMY متطابق الضلعين. 16) رافعات تستعمل رافعات متوازيات الأضلاع لرفع المركبات الثقيلة عند صيانتها. ففي الشكل أدناه: ABEF, BCDE متوازيا أضلاع اكتب برهانا ذا عمودين لإثبات أن ACDF متوازي أضلاع أيضًا. المثال 3 جبر أوجد قيمتي x, y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع. (x) (19 4x - 17 (18 2x+9 (17 (3y+5)* 106° (3y+19) (5y-13) x + 11 2x - 1 (22 (2x+2y) 3x+3y (x+y) (4y+x)/ (21 (20 2y+3 2x+4 3y+5 4y-11 الفصل 5 الأشكال الرباعية 162

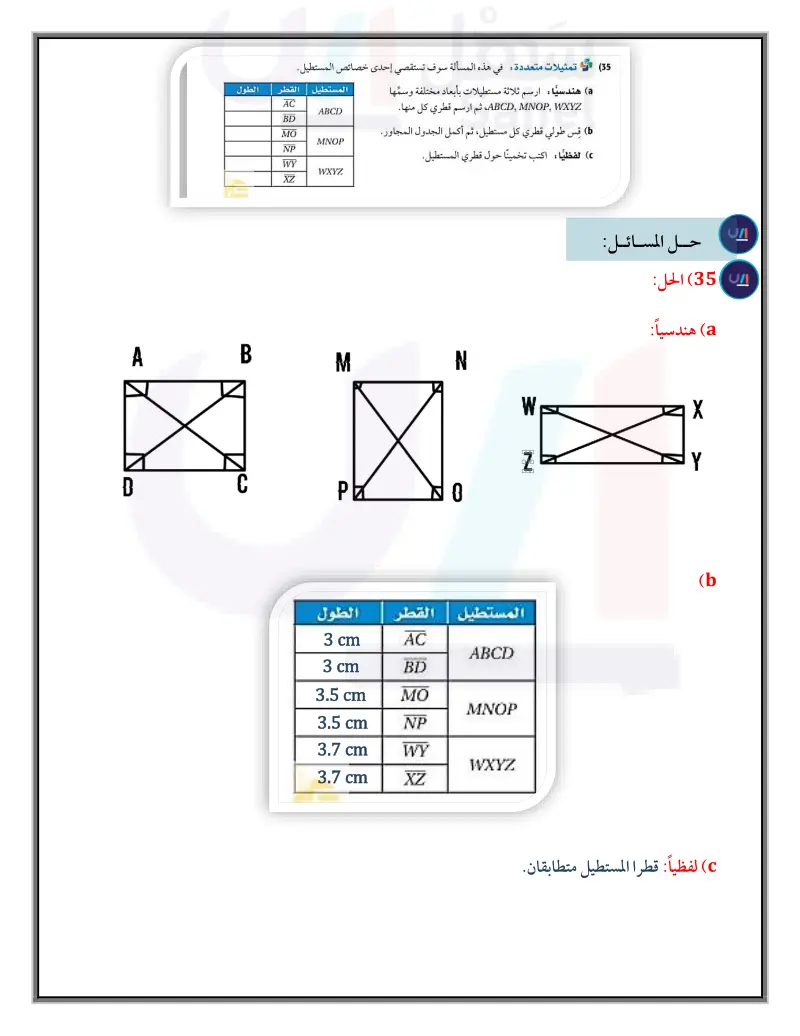
المثال 4 هندسة إحداثية مثل في المستوى الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه فيما يأتي. وحدد ما إذا كان متوازي أضلاع أم لا، برّر إجابتك باستعمال الطريقة المحدّدة في السؤال. JD(-2,-2) C(5, -1) .B(4, 5) A(-3, 4) (23 jbal M(3, -3) L(4, 3) K(-3, 1) J(-4,-4) (24 all. Y(-4, 7) X(-6, 2) .W(1,-2).V(3, 5) (25 26) (24) ، (3) ,4) ، ( 3 ) ، ( 5 ) ، صيغتا الميل والمسافة بين نقطتين. المثال 5 (27) اكتب برهانًا إحداثيا للعبارة: إذا كان كل ضلعين متقابلين في الشكل الرباعي متطابقين، فإنه متوازي أضلاع. 28) اكتب برهانًا إحداثيا للعبارة: إذا كانت إحدى زوايا متوازي الأضلاع قائمة، فإنّ جميع زواياه قوائم. (29) برهان اكتب برهانا حرا للنظرية 5.10. (30) المنسَاخ: استعن بمعلومات الربط مع الحياة إلى اليمين والشكل أدناه. نقطة ثابتة C D رأس القلم نقطة تتبع الشكل الأصلي الربط مع الحياة المنساخ هو أداة هندسية a) إذا كان AC CF AB = CD = BE , DF = DE، فاكتب برهانا حرا لإثبات أن BE || CD . ) مقياس الرسم للشكل المنسوخ بالنسبة للشكل الأصلي هو نسبة CF إلى BE، فإذا كان AB = 12in, F = 8in ، وطول الشكل الأصلي 1.5in فما طول صورة الشكل المنسوخ ؟ تستعمل لنسخ صورة أو مخطط وفق مقياس رسم معين. (31) برهان اكتب برهانا ذا عمودين للنظرية 5.11 أوجد الإحداثيات المجهولة لرؤوس كل من متوازيي الأضلاع الآتيين: Z(-b,c) Y(?, ?) x OW(0, 0) X (a,?) (33 C(?,c) D(?,?) y x OA(0,0) B(a + b, 0) (32 مراجعة المفردات مقياس الرسم : هو نسبة تستعمل لتمثيل الأشياء التي تكون كبيرة جدا أو صغيرة جدا عندما ترسم بحجمها (34) برهان: اكتب برهانًا إحداثيا لإثبات أن القطع المستقيمة الواصلة بين منتصفات أضلاع أي شكل رباعي تشكل متوازي أضلاع. الحقيقي. ويعطي المقياس نسبة تقارن بين قياسات الرسم (35) تمثيلات متعددة في هذه المسألة سوف تستقصي إحدى خصائص المستطيل. أو النموذج وقياسات الأشياء الحقيقية. a) هندسيًّا : ارسم ثلاثة مستطيلات بأبعاد مختلفة وسمها ABCD, MNOP, WXYZ ، ثم ارسم قطري كل منها. ) قس طولي قطري كل مستطيل، ثم أكمل الجدول المجاور. لفظيا : اكتب تخمينا حول قطري المستطيل. المستطيل القطر الطول AC ABCD BD MO MNOP NP WY WXYZ XZ الدرس - تمييز متوازي الأضلاع الـ163يم Ministry of Educo 2024-1446

المنساخ هو أداة هندسية تستعمل لنسخ صورة أو مخطط وفق مقياس رسم معين
مقياس الرسم
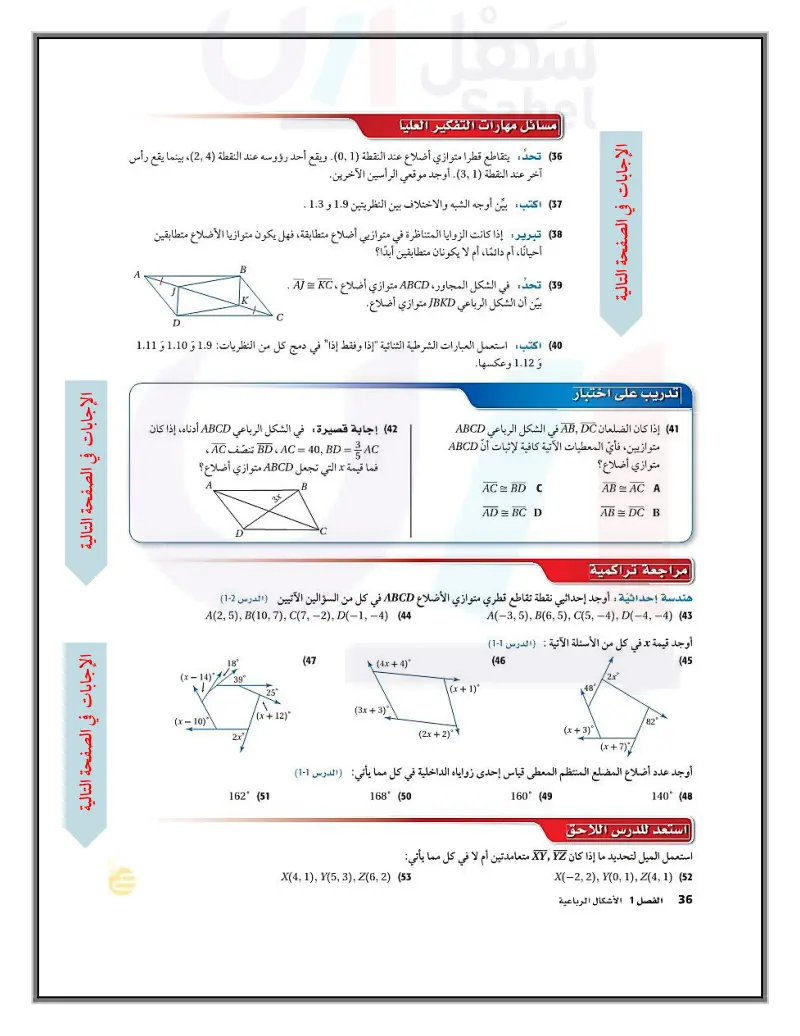
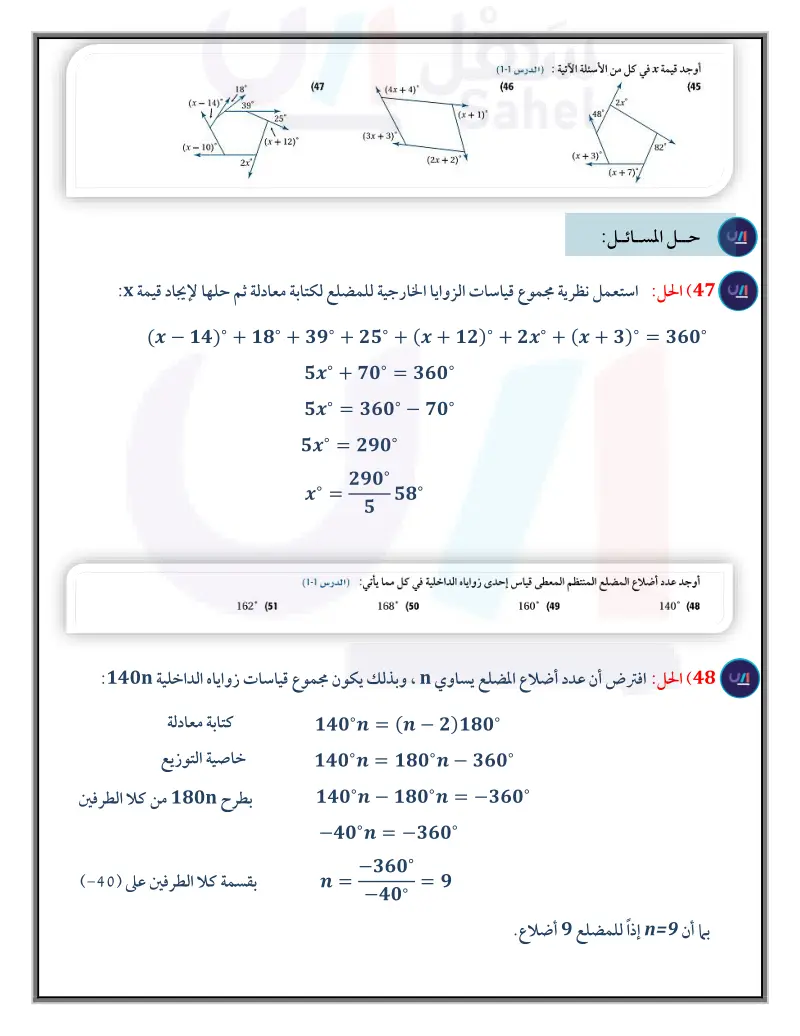
تدريب على اختبار مسائل مهارات التفكير العليا 36) تحد: يتقاطع قطرا متوازي أضلاع عند النقطة (0) . ويقع أحد رؤوسه عند النقطة (24)، بينما يقع رأس آخر عند النقطة (3) أوجد موقعي الرأسين الآخرين. (37) اكتب بين أوجه الشبه والاختلاف بين النظريتين 5.9 و 5.3 . 38 تبرير: إذا كانت الزوايا المتناظرة في متوازيي أضلاع متطابقة، فهل يكون متوازيا الأضلاع متطابقين أحيانًا، أم دائما، أم لا يكونان متطابقين أبدًا؟ 39) تحد في الشكل المجاور، ABCD متوازي أضلاع ، AJ = KC . بين أن الشكل الرباعي JBKD متوازي أضلاع C B 40) اكتب: استعمل العبارات الشرطية الثنائية إذا وفقط إذا" في دمج كل من النظريات: 5.9 و 5.10 و 5.11 و 5.12 وعكسها. (41) إذا كان الضلعان ABC في الشكل الرباعي ABCD متوازيين فأي المعطيات الآتية كافية لإثبات أن ABCD متوازي أضلاع؟ (42) إجابة قصيرة في الشكل الرباعي ABCD أدناه، إذا كان =AC = BD ، AC = 40, BD تنصف AC ، فما قيمة x التي تجعل ABCD متوازي أضلاع؟ وزارة التعليم Ministry of Education 2024-1446 A D B AC = BD C AB AC A AD = BC D AB= DC B مراجعة تراكمية هندسة إحداثية : أوجد إحداثي نقطة تقاطع قطري متوازي الأضلاع ABCD في كل من السؤالين الآتيين (الدرس (2-5) A(2, 5), B(10, 7), C(7, -2), D(-1,-4) (44 18° (x-14) 39° ་་ 25 (47 (4x+4)° (x+1)° (x-10) (x+12)° (3x+3)° 2x° (2x+2) 162° (51 A(-3, 5), B(6, 5), C(5, -4), D(-4,-4) (43 أوجد قيمة x في كل من الأسئلة الآتية : ( الدرس 1-5) (46 48° 2x° 82° (x+3)° (x+7)% (45 أوجد عدد : أضلاع المضلع المنتظم المعطى قياس إحدى زواياه الداخلية في كل مما يأتي: (الدرس 1-5) 168° (50 160° (49 140° (48 استعد للدرس اللاحق استعمل الميل لتحديد ما إذا كان XYZ متعامدتين أم لا في كل مما يأتي: X(4, 1), Y(5, 3), Z(6, 2) (53 الفصل 5 الأشكال الرباعية X(-2, 2), Y(0, 1), Z(4, 1) (52 164

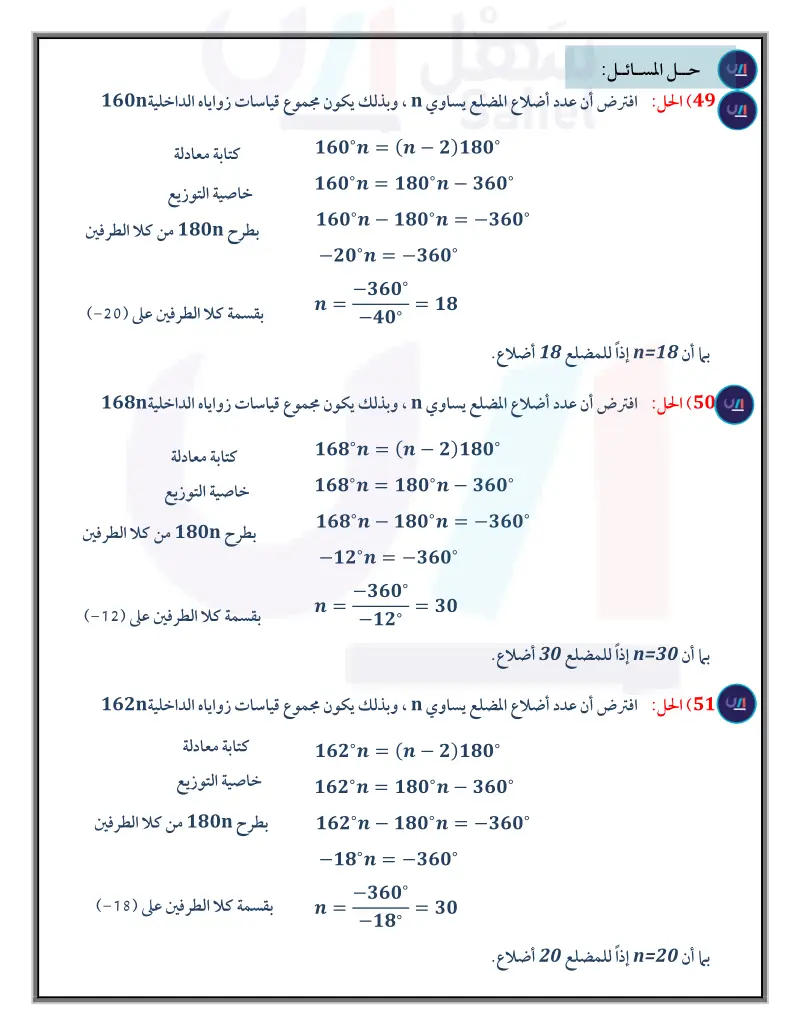
اختبار منتصف الفصل الدروس 1-5 إلى 3-5 الفصل 5 أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعات المحدبة (19) برهان اكتب برهانا ذا عمودين (الدرس (2-5) الآتية : الدرس (51) 1) الخماسي (3) ذو 18 ضلعا (2) السباعي (4) ذو 23 ضلعا أوجد قياسات جميع الزوايا الداخلية في كل من المضلعين المعطيات GFBA, HACD المطلوب : FELD A B H G F D C أوجد قيمتي , x في كل مما يأتي بحيث يكون الشكل الرباعي متوازي 3x 2 (21 6y 8 4y+6 2x+6 أضلاع : (الدرس 3-5) 1 + 10 2x+2 +5 (20 2y+5 (22) طاولات لماذا يبقى سطح طاولة كي الثياب في الصورة أدناه موازيا لأرضية الغرفة دائما؟ (الدرس (3-5) (23) اختيار من متعدّد أي الأشكال الرباعية الآتية ليس متوازي أضلاع؟ (الدرس (3-5) C الآتيين (الدرس 1-5) Q (6 (2x-16) (5 R 2x (4x-26) B D (x+10)\ P (2x+18) C أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قیاسات زواياه الداخلية في كل مما يأتي : (الدرس 1-5) 1260° (8 4500° (10 720° (7 1800° (9 أوجد قيمة x في كل من الشكلين الآتيين : ( الدرس (1-5) (12) (x+4) 56 /(x+10)° \(x-6)° (11 \(x + 15) 106° (x-10)\ (2x-35) استعمل WXYZ لإيجاد كل مما يأتي : (الدرس (2-5) W 105° /24 A Z 28 Y B P 64° هندسة إحداثية : حدد ما إذا كان الشكل الرباعي المعطاة إحداثيات رؤوسه في كل مما يأتي متوازي أضلاع برّر إجابتك باستعمال الطريقة المحددة في السؤال (الدرس (3-5) A(-6,-5), B(-1, -4), C(0, -1), D(-5,-2) (24 صيغة المسافة بين نقطتين. Q(-5, 2), R(-3, -6), S(2, 2), T(-1, 6) (25 الفصل 5 اختبار منتصف الفصلية ال165يم Ministry of Education 2024-1446 صيغة الميل. X MZWZY (13 WZ (14 mZXYZ (15 16 إنارة : استعمل مقبض الإنارة العلوي الذي يشكل متوازي أضلاع في إيجاد mp في PQRS (الدرس (52) جبر: أوجد قيم المتغيرات في كل من متوازيي الأضلاع الآتيين : (الدرس (2-5) J 3f-6 (18 W. K X 56° 8 s-7 6 \(3d-2)° 21-6 M Y 2f+8 L Z (17



 0
0