شبه المنحرف وشكل الطائرة الورقية - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
5-6 شبه المنحرف وشكل الطائرة الورقية Trapezoid and Kite فيما سبق لماذا؟ تستعمل في رياضات القفز ، صناديق ذات أجزاء متداخلة مصنوعة من الإسفنج ذي الضغط درست استعمال خصائص العالي، وتتخذ منصات وثب ودرجات صعود، وتمثل جوانب كل من الأجزاء شبه منحرف. أنواع خاصة من متوازي الأضلاع الدرس (55) والان - أتعرف خصائص شبه المنحرف وأطبقها. . أتعرف خصائص شكل الطائرة الورقية وأطبقها. المفردات: شبه المنحرف trapezoid قاعدتا شبه المنحرف bases ساقا شبه المنحرف legs of a trapezoid زاويتا القاعدة base angles شبه المنحرف المتطابق الساقين isosceles trapezoid القطعة المتوسطة لشبه المنحرف midsegment of a trapezoid خصائص شبه المنحرف شبه المنحرف هو شكل رباعي فيه ضلعان فقط متوازيان يُسميان قاعدتي شبه المنحرف ويُسمّى الضلعان غير المتوازيين ساقي شبه المنحرف و زاويتا القاعدة مكوّن كل منهما من قاعدة وأحد ضلعي الساقين. ففي شبه المنحرف ABCD المبين جانبا ، A B زاويتا القاعدة AB ، وكذلك CD زاويتا القاعدة DC . إذا كان ساقا شبه المنحرف متطابقين فإنه يسمى شبه منحرف متطابق الساقين. نظريات شبه المنحرف المتطابق الساقين 5.21 إذا كان شبه المنحرف متطابق الساقين، فإن زاويتي كل قاعدة متطابقتان. مثال: إذا كان شبه المنحرف FGHJ متطابق الساقين . ZG ZH, ZFZJ 5.22 إذا كانت زاويتا قاعدة في شبه المنحرف متطابقتين، فإنه متطابق الساقين. مثال : إذا كان KLMP شبه منحرف فيه LEM فإنه متطابق الساقين. 5.23 يكون شبه المنحرف متطابق الساقين، إذا وفقط إذا كان قطراه متطابقين. مثال: إذا كان شبه المنحرف QRST متطابق الساقين فإن QS = RT . وكذلك إذا كان QRST شبه منحرف فيه QS = RT فإنه متطابق الساقين. C ساق H www.icn.edu.sa B قاعدة A ساق قاعدة أضف إلى D مطويتك M P R S سوف تبرهن النظريات 5.225.23 5.21 في الأسئلة 1901 على الترتيب. شكل الطائرة الورقية kite 180 الفصل 5 الأشكال الرباعية برهان الحالة الأولى من النظرية 5.23 المعطيات ABCD شبه منحرف متطابق الساقين. المطلوب : AC = BD ABCD شبه منحرف متطابق الساقين. ZADC= ZBCD معطى AD = BC زاويتا قاعدة شبه المنحرف تعريف شبه المنحرف المتطابق الساقين متطابقتان المتطابق الساقين AADC = ABCD SAS DC=CD خاصية الانعكاس للتطابق AC = BD ضلعان متناظران في مثلثين متطابقين A B وزارة التعليم Ministry of Education 2024-1446

W إرشادات للدراسة شبه المنحرف المتطابق الساقين مثال 1 من واقع الحياة استعمال خصائص شبه المنحرف المتطابق الساقين مكبرات الصوت المنظر الأمامي لمكبر الصوت المبين جانبا على شكل شبه منحرف متطابق الساقين. إذا كان °85 = m/FJH، تكون زاويتا كل قاعدة FK = 8 in, JG = 19 in ، فأوجد كلا مما يأتي : في شبه المنحرف متطابقتين فقط إذا كان شبه المنحرف متطابق الساقين. mZFGH (a بما أن FGHJ شبه منحرف متطابق الساقين، فإن FJH و LGH زاويتا قاعدة متطابقتان؛ لذا فإن .mZGHJ = mZFJH = 85° وبما أن FGHJ شبه منحرف، فإن FG || JH . mZFGH + mZGHJ = 180° mZFGH+85° = 180° mZFGH = 95" H نظرية الزاويتين المتحالفتين بالتعويض بطرح 85 من كلا الطرفين G F KH (b بما أن FGHJ شبه منحرف متطابق الساقين، فإنّ القطرين FH و JG متطابقان. تعريف تطابق القطع المستقيمة مسلمة جمع القطع المستقيمة بالتعويض بطرح 8 من كلا الطرفين Y X Z FH = JG FK + KH = JG 8 + KH = 19 KH = ll in تحقق من فهمك 1 مطاعم لاستغلال مساحة الطاولات المربعة تستعمل في مطعم أطباق على شكل شبه منحرف كما في الشكل المجاور. إذا كان WXYZ شبه منحرف متطابق الساقين، وكان mZYZW = 85°, WV = 15cm، VY = 10 cm، فأوجد كلا مما يأتي : XZ (C mZWXY (B mZXWZ (A يمكنك استعمال الهندسة الإحداثية لتحديد ما إذا كان شبه المنحرف متطابق الساقين أم لا. بين مثال 2 شبه المنحرف المتطابق الساقين والهندسة الإحداثية هندسة إحداثية رؤوس الشكل الرباعي ABCD هي (10) ,(33) ,5 ,B2 ,4 ,3). ، أن ABCD شبه منحرف، وحدد ما إذا كان متطابق الساقين. ووضّح إجابتك. ارسم الشكل الرباعي ABCD في مستوى إحداثي. الخطوة 1: استعمل صيغة الميل لمقارنة ميلي الضلعين المتقابلين BC, AD وكذلك الضلعين المتقابلين . فالشكل الرباعي يكون شبه منحرف إذا كان فيه ضلعان فقط متقابلان متوازيين B A D 10 الدرس - شبه المنحرف وشكل الطائرة الورقية ال181يم Ministry of Educatio 2024-1446 الربط مع الحياة مكبرات الصوت هي مضخمات تُكثف الأمواج الصوتية حتى تصبح مسموعة بدرجة أكبر. ويحتوي كل من المذياع والتلفاز والحاسوب مضخمات صوتية.

تستعمل في مطعم أطباق على شكل شبه منحرف كما في الشكل إذا كان wxyz شبه منحرف متطابق الساقين أوجد كلا مما يأتي


مكبرات الصوت هي مضخمات تكثف الأمواج الصوتية حتى تصبح مسموعة بدرجة أكبر
A 4y D 10 الضلعان المتقابلان BCAD: 3-5-=-=-2 =-2 0-4 -4=-2 -1-(-3) = میل BC : میل AD: بما أن ميلي BC,AD متساويان، فإن BC ||AD الضلعان المتقابلان ABC : 5 2-(-3) - 4 میل AB : - میل DC : قراءة الرياضيات رمز التوازي: تذكر أن الرمز || يعني يوازي والرمز | يعني لا يوازي. بما أن ميلي AB و DC ليسا متساويين، فإنّ ABDC . وبما أن ABCD فيه ضلعان فقط متوازیان، فإنّه شبه منحرف. الخطوة 2 استعمل صيغة المسافة بين نقطتين للمقارنة بين طولي الساقين ABDC وتحديد ما إذا كان شبه المنحرف ABCD متطابق الساقين. AB (-3-2)² + (4-5)² = √√26 DC = V (-1 - 32 + (0 - 32 = V25 = 5 قراءة الرياضيات القطعة المتوسطة : تسمى القطعة المتوسطة لشبه بما أن AB DC ، فإنّ شبه المنحرف ABCD ليس متطابق الساقين. تحقق من فهمك .Q(-8, -4), R(0, 8), S(6, 8), T(-6, -10) (2) رؤوس الشكل الرباعي QRST هي ) بين أن QRST شبه منحرف، وحدد ما إذا كان متطابق الساقين. ووضّح إجابتك. هي القطعة المتوسطة لشبه المنحرف ، قطعة مستقيمة تصل بين منتصفي ساقيه وتبين النظرية الآتية العلاقة بين القطعة المتوسطة وقاعدتي شبه المنحرف القطعة المتوسطة أضف إلى مطويتك وزارة التعليم Ministry of Education 2024-1446 # C B نظرية 5.24 نظرية القطعة المتوسطة لشبه المنحرف القطعة المتوسطة لشبه المنحرف توازي كلا من القاعدتين، وطولها يساوي نصف مجموع طولي القاعدتين. مثال: إذا كانت BE قطعة متوسطة لشبه المنحرف ACDF ، فإن AF || BE, CD || BE ، # E D سوف تبرهن النظرية 5.24 في السؤال 25 . .BE = { (AF + CD) المنحرف أيضًا القطعة المنصفة. الفصل 5 الأشكال الرباعية 182

رمز التوازي
S F x G 15 L K 18.2 H مثال 3 من اختبار في الشكل المجاور، LH قطعة متوسطة الشبه المنحرف FGJK ما قيمة x؟ اقرأ سؤال الإختبار أعطيت في السؤال طول القطعة المتوسطة لشبه المنحرف وطول إحدى قاعدتيه. ويطلب إليك إيجاد طول القاعدة الأخرى. حل سؤال الاختبار نظرية القطعة المتوسطة لشبه المنحرف P # Q R بالتعويض بضرب كلا الطرفين في 2 بطرح 18.2 من كلا الطرفين LH = } (FG + KJ) 15 = (x + 18.2) 30 x+18.2 11.8 = x تحقق من فهمك 3) في الشكل أدناه، QR قطعة متوسطة لشبه المنحرف LMNP . ما قيمة x؟ . 4x - 10 L M 5 Q R 8 P N خصائص شكل الطائرة الورقية شكل الطائرة الورقية هو شكل رباعي يتكون من زوجين متمايزين من الأضلاع المتجاورة المتطابقة. وعلى عكس متوازي الأضلاع، كل ضلعين متقابلين في شكل الطائرة الورقية ليسا متطابقين ولا متوازيين. الدرس - شبه المنحرف وشكل الطائرة الورقية ال183م Ministry of Educati 2024-1446

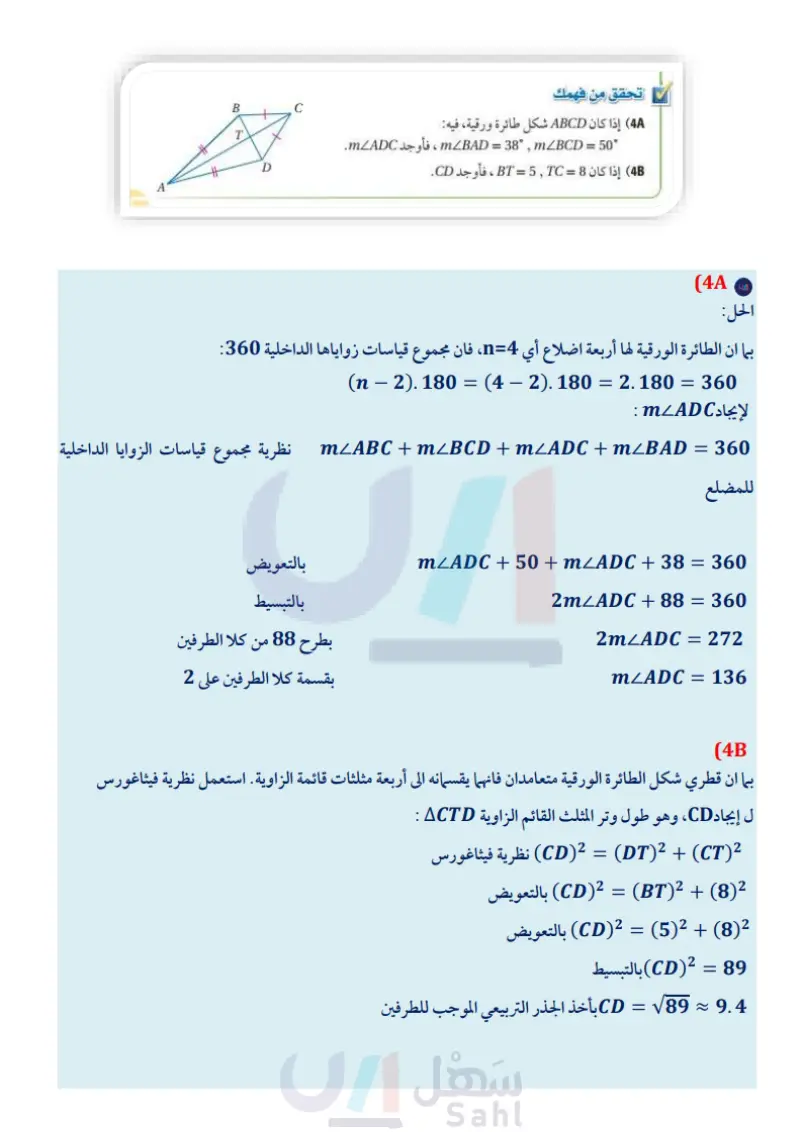
نظريات شكل الطائرة الورقية 5.25 قطرا شكل الطائرة الورقية متعامدان مثال : بما أن ABCD شكل طائرة ورقية ، فإن AC 1 BD C 5.26 يوجد في شكل الطائرة الورقية زوج واحد فقط من الزوايا المتقابلة المتطابقة هما الزاويتان المحصورتان بين كل ضلعين متجاورين غير متطابقين. مثال: بما أن JKLM شكل طائرة ورقيّة، فإنّ , . L B أضف إلى مطويتك A # K D سوف تبرهن النظريتين 5.26, 5.25 في السؤالين 223 على الترتيب. M يمكنك استعمال النظريتين أعلاه ونظرية فيثاغورس ونظرية مجموع قياسات الزوايا الداخلية للمضلع لإيجاد القياسات المجهولة في شكل الطائرة الورقية. مثال 4 استعمال خصائص شكل الطائرة الورقية ) إذا كان FGHJ شكل طائرة ورقية، فأوجد mF. في شكل الطائرة الورقية زوج واحد فقط من الزوايا المتقابلة المتطابقة، وبما أن ( LG ، فإن F = H ؛ لذلك mZF = mZH . اكتب معادلة وحلّها لإيجاد mZF. mZF+mZG+mZH+m/J = 360° mZF + 128° + mZF + 72° = 360° 2mZF+200° = 360° 2mZF = 160° نظرية مجموع قياسات الزوايا الداخلية للمضلع بالتعويض بالتبسيط 128° F H 72° الربط مع الحياة أقصى سرعة مسجلة لطائرة ورقية 120mih وأقصى ارتفاع مسجل لطائرة ورقية ft 12471 mZF = 80° بطرح 200 من كلا الطرفين بقسمة كلا الطرفين على 2 ) إذا كان WXYZ شكل طائرة ورقية فأوجد ZY . بما أن قطري شكل الطائرة الورقية متعامدان فإنهما يقسمانه إلى أربعة مثلثات قائمة الزاوية. استعمل نظرية فيثاغورس لإيجاد ZY، وهو طول وتر المثلث القائم الزاوية AYPZ. نظرية فيثاغورس PZ2 + PY2 = ZY2 82 + 242 = ZY 2 640=ZY2 √640=ZY 8V10 = ZY بالتعويض بالتبسيط X 8 6 W 24 P Y 8 Z بأخذ الجذر التربيعي الموجب للطرفين بالتبسيط 184 الفصل 5 الأشكال الرباعية تحقق من فهمك 4) إذا كان ABCD شكل طائرة ورقية، فيه 50 = mLBAD = 38", mBCD ، فأوجد mLADC. 4) إذا كان 8 = BT = 5TC ، فأوجد CD. B + C T وزارة التعليم Ministry of Education 2024-1446

أقصى سرعة مسجلة لطائرة ورقية 120 ml/ h
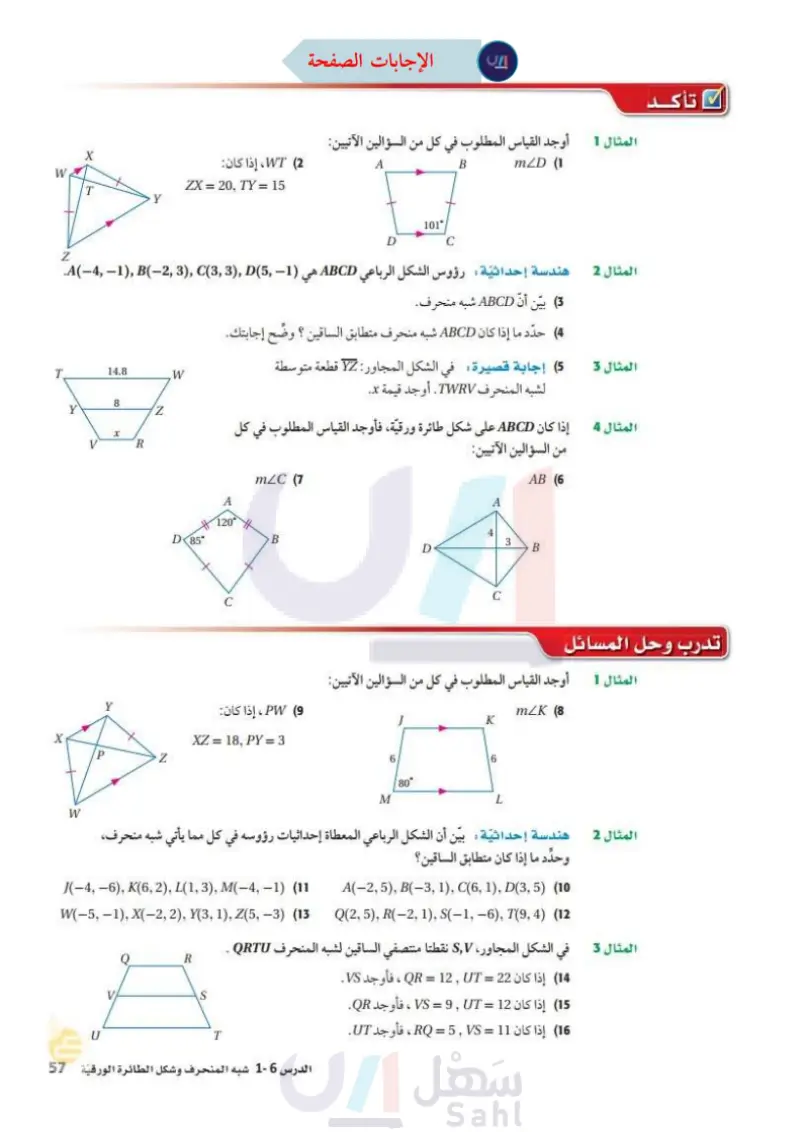
W X (2) WT ، إذا كان ZX = 20, TY = 15 T Y Z .A(-4, -1), B(-2, 3), C(3, 3), D(5, -1), T 14.8 .W Y 8 V x X P W y R D 85° أوجد القياس المطلوب في كل من السؤالين الآتيين المثال 1 A D 101° C B mZD (1 هي المثال 2 هندسة إحداثية رؤوس الشكل الرباعي ABCD هم 3 بين أن ABCD شبه منحرف. المثال 3 (4) حدد ما إذا كان ABCD شبه منحرف متطابق الساقين ؟ وضّح إجابتك. (5) إجابة قصيرة في الشكل المجاور: YZ قطعة متوسطة الشبه المنحرف TWRV . أوجد قيمة x. إذا كان ABCD على شكل طائرة ورقية، فأوجد القياس المطلوب في كل المثال 4 من السؤالين الآتيين: mZC (7 AB (6 A 120 B D B C تأكد تدرب وحل المسائل أوجد القياس المطلوب في كل من السؤال المثال 1 الآتيين: mZK (8 K 9) PW ، إذا كان I XZ = 18, PY = 3 Z 6 6 80° M L هندسة إحداثية : بين أن الشكل الرباعي المعطاة إحداثيات رؤوسه في كل مما يأتي شبه منحرف، المثال 2 وحدد ما إذا كان متطابق الساقين؟ J(-4, -6), K(6, 2), L(1, 3), M(-4, -1) (11 W(-5, -1), X(-2, 2), Y(3, 1), Z(5,-3) (13 A(-2, 5), B(-3, 1), C(6, 1), D(3,5) (10 Q(2, 5), R(-2, 1), S(-1, -6), T(9,4) (12 R VA S T في الشكل المجاور، V, نقطتا منتصفي الساقين لشبه المنحرف QRTU المثال 3 (14) إذا كان 22 = QR = 12, UT ، فأوجد VS . (15) إذا كان 12 = VS = 9 ,UT ، فأوجد QR . الدرس - شبه المنحرف وشكل الطائرة الورقية ال185يم Ministry of Education 2024-1446 (16) إذا كان 11 = RQ = 5, VS ، فأوجد UT

X المثال 4 إذا كان WXYZ شكل طائرة ورقية، فأوجد القياس المطلوب في كل مما يأتي : W 70° 56° Y Z mX (18 X 6 4 W Y P WP (17 الربط مع الحياة تمتاز الأصص الفخارية بالمسامية والتهوية برهان اكتب برهانا حرا لكل من النظريات الآتية : 19) النظرية 5.21 (22) النظرية 5.25 (20) النظرية 5.22 (21) النظرية 5.23 (23) النظرية 5.26 (24) نباتات اشترى مشاري أصيصًا زراعياً أوجهه الأربعة على شكل شبه منحرف أبعاده كما في الشكل المجاور. إذا أراد مشاري وضع رف أفقي عند منتصف الأصيص؛ لتستند إليه النبتة، فكم يكون عرض هذا الرف؟ (25) برهان اكتب برهانًا إحداثيا للنظرية 5.24. وصرف المياه الزائدة ما (26) هندسة إحداثية: استعن بالشكل الرباعي ABCD المجاور. يسمح بنمو جيد للجذور وهي من أفضل الأصص الزراعية. بين أن ABCD شبه منحرف. وحدد ما إذا كان متطابق الساقين. وضح إجابتك. (6) هل القطعة المتوسطة محتواة في المستقيم الذي معادلته 1 + y = -x؟ برّر إجابتك . أوجد طول القطعة المتوسطة. 26 in 14 in- A(-3,2) Ay B(1,3) C(5, 0) 0 -D(5,-4) جبر في الشكل المجاور، ABCD شبه منحرف أوجد قيمة x بحيث يكون متطابق الساقين في كل مما يأتي: (27) إذا كان 8 + AC = 3x - 7, BD = 2x (28) إذا كان " (33) + (mZABC = (4x + 11) ", mLDAB = (2x جبر في الشكل المجاور، نقطتا منتصفي الساقين لشبه المنحرف QRST . (29) إذا كان QR = 116, PM = 12, TS = 4x ، فأوجد قيمة x. (30) إذا كان TS = 2x, PM = 20, QR = 6x ، فأوجد قيمة x. (31) إذا كان 10 = PM = 2x, QR = 33x, TS ، فأوجد PM. (32) إذا كان 13 = 3 + TS = 2x + 2, QR = 5x ، فأوجد TS تسوق الوجه الجانبي لحقيبة التسوّق المبينة جانبًا على شكل شبه منحرف متطابق الساقين. إذا كان EC = 9 in, DB = 19 in ، "35 = mLABE = 40°, mLEBC ، فأوجد كلا مما يأتي: B B P D C A Q R P M T S وزارة التعليم Ministry of Education 2024-1446 D AC (34 mZEDC (36 AE (33 mZBCD (35 الفصل 5 الأشكال الرباعية 186

تمتاز الأصص الفخارية بالمسامية والتهوية وصرف المياة الزائدة، ما يسمح بنمو جيد للجذور.
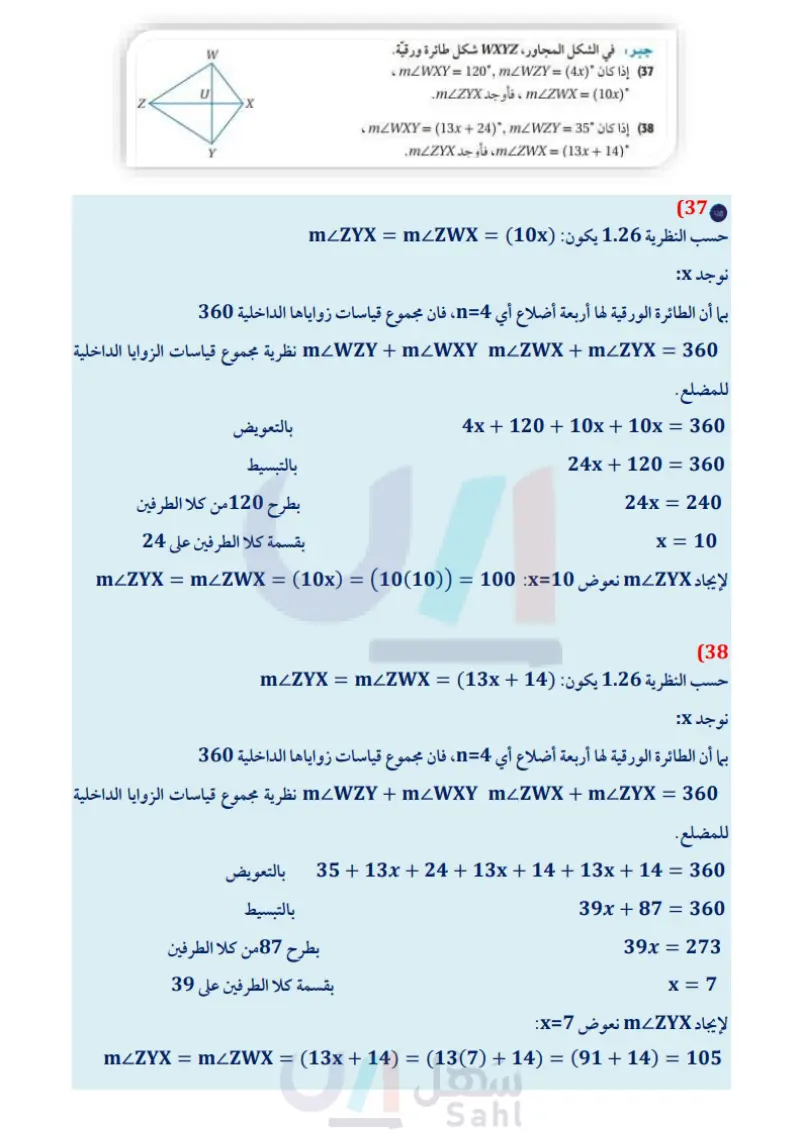
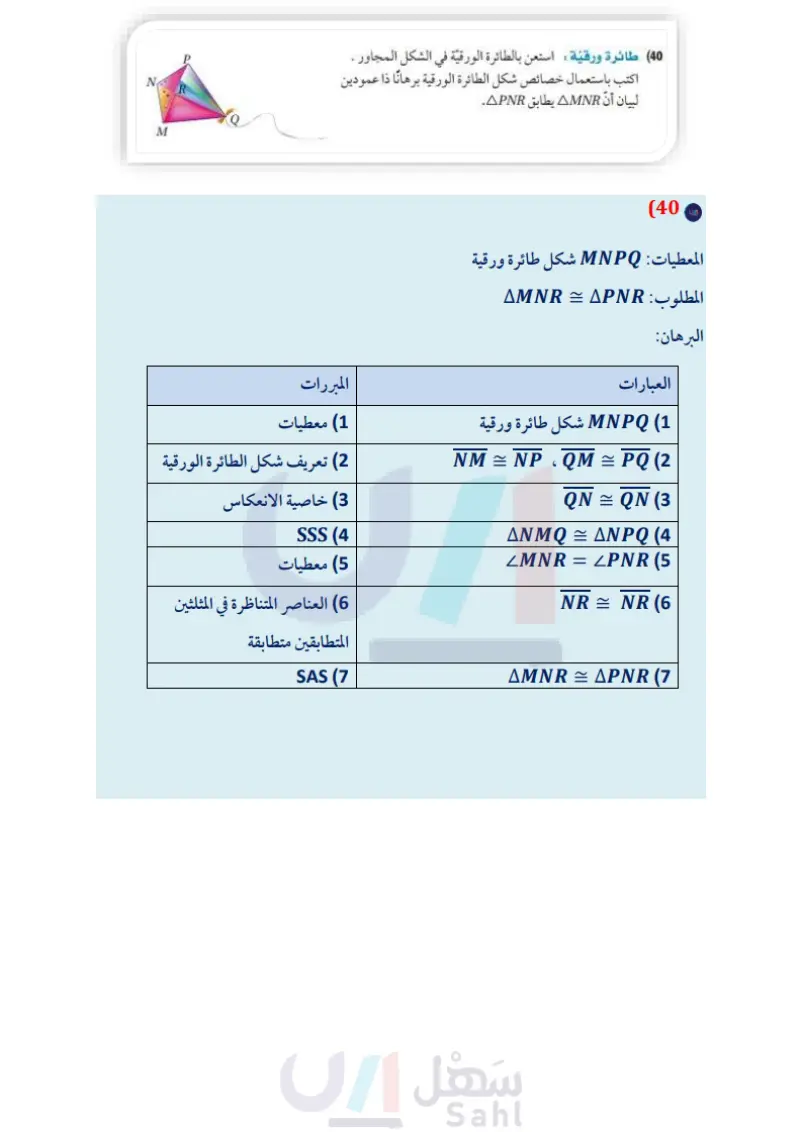
W X V NA M W U X Y Z جبر في الشكل المجاور ، WXYZ شكل طائرة ورقية. (37) إذا كان " (mZWXY = 120°, m<WZY = (4x ، (mZZWX = (10x ، فأوجد mZZYX. (38) إذا كان 35 = mZWXY = (13x + (24)", mLWZY ، (14) + mZZWX = (13x، فأوجد mZZYX. برهان اكتب برهانا ذا عمودين. 39 المعطيات: XY WE = WWE ZXY تنصف كلا من WZ و ZV . المطلوب: WXYV شبه منحرف متطابق الساقين. (40) طائرة ورقية : استعن بالطائرة الورقية في الشكل المجاور . اكتب باستعمال خصائص شكل الطائرة الورقية برهانا ذا عمودين لبيان أن AMNR يطابق APNR (41) أشكال فن ارسم شكل فن يوضح جميع الأشكال الرباعية متضمناً شبه المنحرف المتطابق الساقين، وشكل الطائرة الورقية وعموم الأشكال الرباعية التي لا أسماء خاصة لها. هندسة إحداثية: حدد ما إذا كان الشكل المعطاة إحداثيات رؤوسه في كل مما يأتي شبه منحرف، أم متوازي أضلاع، أم مستطيلا، أم مربعًا، أم معينا، أم هو شكل رباعي فحسب؟ اختر أكثر المسميات تحديدا، ووضح إجابتك. W(-3, 4), X(3, 4), Y(5, 3), Z(-5, 1) (43 B C A(-1, 4), B(2, 6), C(3, 3), D(0, 1) (42 (44) تمثيلات متعددة : سوف تستقصي في هذه المسألة إحدى خصائص شكل الطائرة الورقية. a) هندسيا : ارسم قطعة مستقيمة. وأنشئ عمودًا منصفًا لها لا تنصفه القطعة المستقيمة ولا تساويه طولاً. ثم صل أطراف القطعتين المستقيمتين لتكون الشكل الرباعي ABCD كما في الشكل المجاور كرّر هذه العملية مرتين، وسم الشكلين الرباعيين الجديدين PQRS, WXYZ جدوليا : انقل الجدول الآتي وأكمله. الشكل الضلع الطول الضلع الطول الضلع الطول الضلع الطول DA SP ZW CD RS YZ BC QR XY AB ABCD PQ PQRS WX WXYZ لفظيا : اكتب تخمينا حول الشكل الرباعي الذي قطراه متعامدان وغير متطابقين، وأحدهما فقط ينصف الآخر . برهان اكتب برهانًا إحداثيا لكل من العبارتين الآتيتين : (45) قطرا شبه المنحرف المتطابق الساقين متطابقان. 46) القطعة المتوسطة لشبه المنحرف المتطابق الساقين توازي كلًا من القاعدتين. الدرس - شبه المنحرف وشكل الطائرة الورقية ال187يم Ministry of Educatio 2024-1446

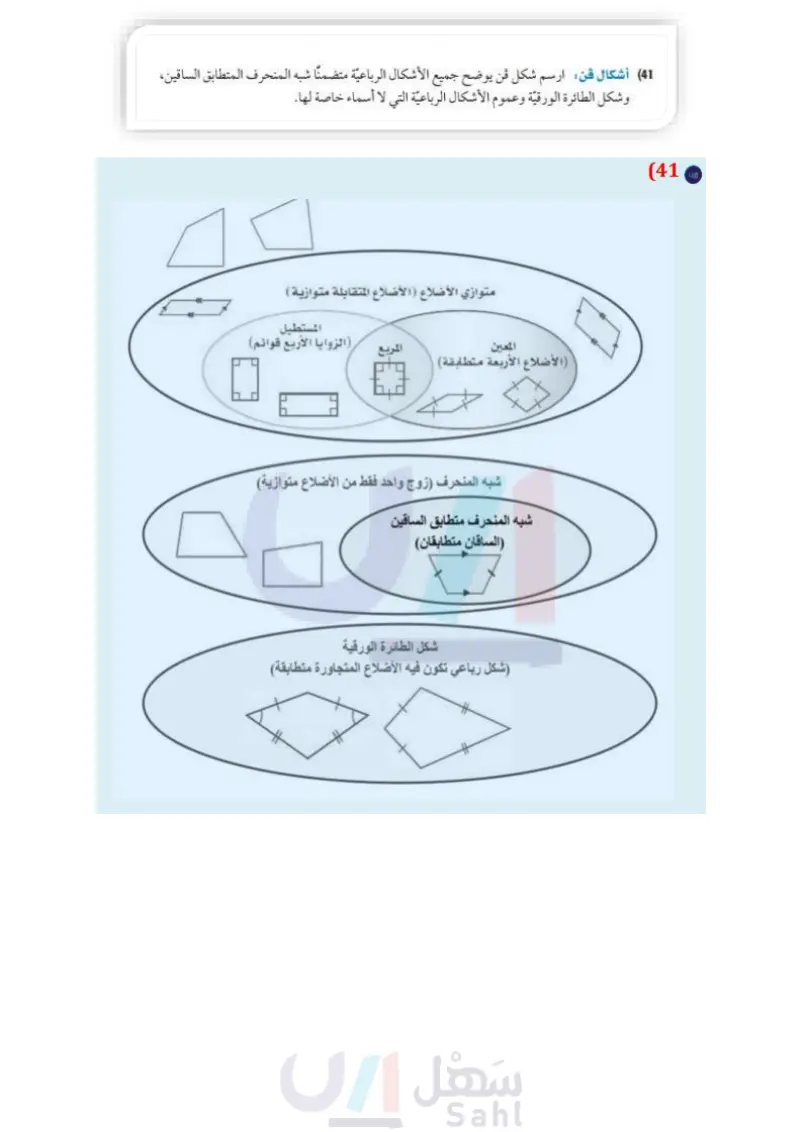
ارسم شكل فن يوضح جميع الاشكال الرباعية متضمنا شبه المنحرف المتطابق الساقين وشكل الطائرة الورقية وعموم الأشكال الرباعية التي لا اسماء خاصة لها.


A D 100° B 45' C مسائل مهارات التفكير العليا (47) اكتشف الخطأ أوجد كل من عادل وسعيد mA في شكل الطائرة الورقية ABCD المجاور . هل إجابة أي منهما صحيحة ؟ وضح إجابتك. سعيد m LA= 45° عادل W LA = 115 تدريب على اختبار (48) تحد: إذا كان الضلعان المتوازيان في شبه منحرف محتويين في المستقيمين 8 - y = x + 4, y = x ، فما معادلة المستقيم الذي يحتوي القطعة المتوسطة لشبه المنحرف؟ (49) تبرير: هل العبارة " المربع هو أيضًا شكل طائرة ورقية " صحيحة أحيانًا أم دائما أم غير صحيحة أبدًا ؟ وضح إجابتك. (50) مسألة مفتوحة ارسم شبه المنحرف ABCD ، وشبه المنحرف FGHJ غير المتطابقين وفيهما AC = FH و BD = GJ . 51) اكتب قارن بين خصائص كلِّ من شبه المنحرف وشبه المنحرف المتطابق الساقين وشكل الطائرة الورقية. (52) إذا كان ABCD شكل طائرة ورقية، فما قياس LC؟ B (53) ما الشكل الذي يمكن أن يكون مثالا مضادا للتخمين الآتي؟ إذا كان قطرا شكل رباعي متطابقين فإنه مستطيل . وزارة التعليم Ministry of Education 2024-1446 المربع المعين متوازي الأضلاع شبه المنحرف المتطابق الساقين D M H G F M D DF E A<74° C 105 D مراجعة تراكمية جبر: استعن بالمعين DFGH فيما يأتي: (الدرس 5-5) (54) إذا كان 118 = mFGH ، فأوجد mMHG. (55) إذا كان 6 + DM = 4x - 3, MG = x ، فأوجد DG. (56) إذا كان 15 = HM = 12 HD ، فأوجد MG. (57) برهان اكتب برهانا ذا عمودين (الدرس 5-5) المعطيات CMF = EMF ، ZCFMZEFM المطلوب ADMC = ADME استعد للدرس اللاحق أوجد ميل القطعة المستقيمة المعطاة إحداثيات طرفيها في كل مما يأتي: (y, x), (y, y) (60 (-x, 5x), (0, 6x) (59 (x, 4y), (-x, 4y) (58 الفصل 5 الأشكال الرباعية 188

الفصل 5 دليل الدراسة والمراجعة ملخص الفصل المفاهيم الأساسية زوايا المضلع (الدرس 1-5) . يعطى مجموع قياسات الزوايا الداخلية لمضلع محدب بالصيغة 2.180 - S = (n، حيث " عدد الأضلاع . المفردات الأساسية القطر (ص. 140) ساقا شبه المنحرف (ص. 180) متوازي الأضلاع (ص. 149) زاويتا القاعدة (ص. 180) المستطيل (ص. 166) المعين (ص. 172) المربع (ص. 173) . مجموع قياسات الزوايا الخارجيّة لمضلع محدّب بأخذ زاوية شبه المنحرف (ص. 180) واحدة عند كل رأس يساوي 360. : (الدرسان 2-5 و 53 خصائص متوازي الأضلاع . كل ضلعين متقابلين متطابقان. . كل زاويتين متقابلتين متطابقتان . كل زاويتين متحالفتين متكاملتان . إذا كانت إحدى الزوايا قائمة، فإن الزوايا الأخرى قوائم. القطران ينصف كل منهما الآخر. قطره يقسمه إلى مثلثين متطابقين. خصائص المستطيل والمعين والمربع وشبه المنحرف وشكل الطائرة الورقية ( الدروس 4-5 إلى 6-5 . للمستطيل جميع خصائص متوازي الأضلاع. وقطراه متطابقان. وزواياه الأربع قوائم أضلاعه . للمعين جميع خصائص متوازي الأضلاع وجميع أ متطابقة، وقطراه متعامدان، وينصفان زواياه. للمربع جميع خصائص متوازي الأضلاع والمستطيل والمعين. . زاويتا كل قاعدة في شبه المنحرف المتطابق الساقين متطابقتان، والقطران متطابقان أيضًا. . قطرا شكل الطائرة الورقية متعامدان، ويوجد فيه زوج واحد فقط من الزوايا المتقابلة المتطابقة هما الزاويتان المحصورتان بين كل ضلعين متجاورين غير متطابقين. المطويات منظم أفكار تأكد من أن المفاهيم الأساسية مدونة في مطويتك. الأشكال الرباعية 5-1 5-2,5-3 5-4 5-5 5-6 قاعدتا شبه المنحرف (ص. 180) اختبار المفردات شبه المنحرف المتطابق الساقين (ص. 180) القطعة المتوسطة الشبه المنحرف (ص. 182) شكل الطائرة الورقية (ص. 183) بين ما إذا كانت كل جملة مما يأتي صحيحةٍ أو غير صحيحة ، وإذا كانت غير صحيحة فاستبدل بالكلمة التي تحتها خط كلمة من القائمة أعلاه لتجعل الجملة صحيحة: 1) زاويتا قاعدة شبه المنحرف متطابقتان. (2) إذا كان متوازي الأضلاع مستطيلا، فإن قطريه متطابقان. (3) القطعة المتوسطة لشبه المنحرف تصل بين رأسين غير متتالين فيه. (4 قاعدة شبه المنحرف هي إحدى ضلعيه المتوازيين. (5 قطرا المعين متعامدان 6) قطر شبه المنحرف قطعة مستقيمة تصل بين نقطتي منتصفي ساقيه. (7) المستطيل يكون دائما متوازي أضلاع 8) الشكل الرباعي الذي فيه زوج واحد من الأضلاع المتوازية هو متوازي أضلاع. (9) المعين الذي إحدى زواياه قائمة مستطيل. 10) ساق شبه المنحرف هو أحد ضلعيه غير المتوازيين. الفصل 5 دليل الدراسة والمراجعة ال189يم Ministry of Education 2024-1446

المفردات الاساسية
بين فيما اذا كانت كل جملة فيما يـأتي صحيحة اوغير صحيحة، وإذا كانت غير صحيحة فاستبدل بالكلمة التي تحتها خط كلمة من القائمة أعلاه تجعل الجملة صحيحة

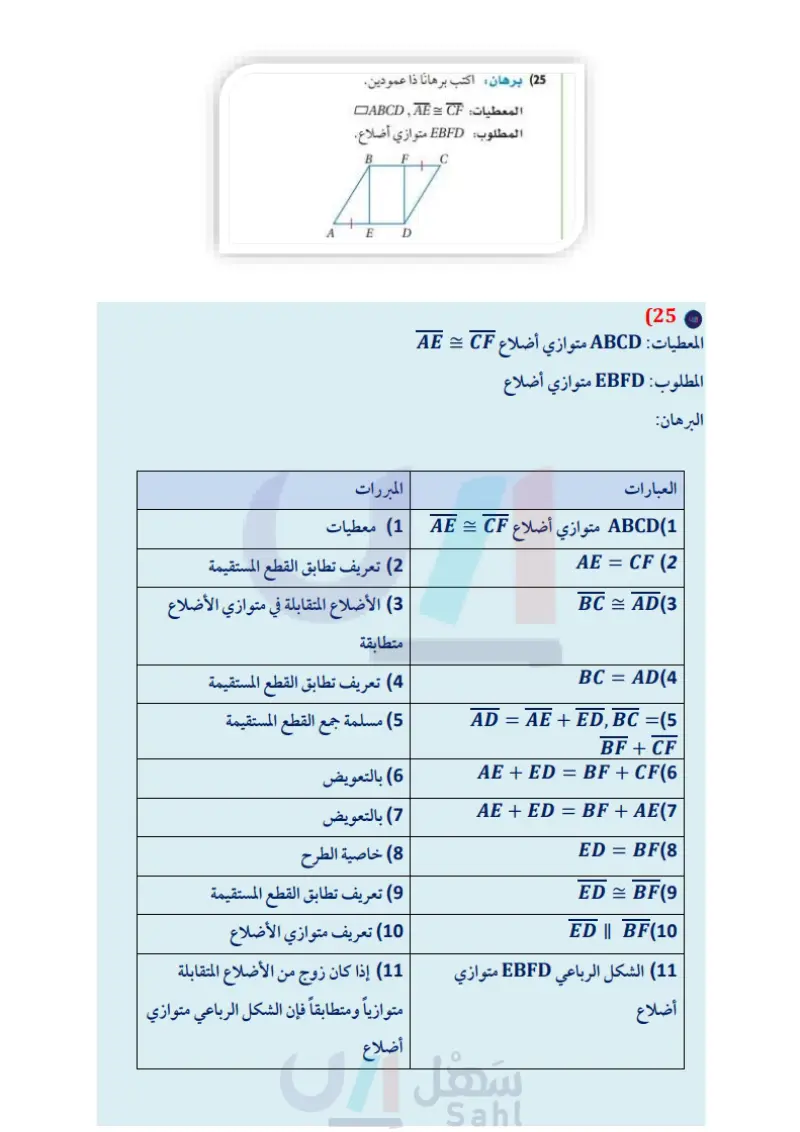
زوايا المضلع
خصائص متوازي الاضلاع
خصائص المستطيل والمربع والمعين وشبة المنحرف وشكل الطائرة الورقية
الفصل 5 دليل الدراسة والمراجعة مراجعة الدروس 5-1 زوايا المضلع (ص 140-148 أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين : 11) العشاري. (12) ذو 15 ضلعا . 13) زخرفة : يمثل نموذج الزخرفة المجاور شكلًا سداسيا منتظما. أوجد مجموع قياسات زواياه الداخلية. مثال 1 أوجد مجموع قياسات الزوايا الداخلية لمضلع محدب عدد أضلاعه 22 ضلعا . S = (n - 2) .180" = (22-2) 180° = 20.180° = 3600° مثال 2 بكتابة معادلة بالتعويض بالطرح بالضرب قياس زاوية داخليّة لمضلع منتظم 157.5. أوجد عدد أضلاعه. أوجد عدد أضلاع المضلع المنتظم المعطى قياس إحدى زواياه الداخلية في كل مما يأتي: 135° (14 168° (15 157.5n = (n - 2) .180" 157.5°n 180°n - 360° -22.5 n-360° n = 16 إذن عدد أضلاع المضلع 16 ضلعا. بكتابة المعادلة خاصية التوزيع بالطرح بالقسمة 5-2 متوازي الأضلاع (ص 149-156) استعمل ABCD المبين جانبًا لإيجاد كل مما يأتي : mZADC (16 AD (17 AB (18 mZBCD (19 B A 115° 18 D 12 C مثال 3 جبر: إذا كان KLMN متوازي أضلاع، فأوجد قيمة المتغير في كل مما يأتي : L 3y-7 9x 36 y+15 N M جبر: أوجد قيمتي , x في كل من متوازيي الأضلاع الآتيين: x (a KN = LM 2y+ 19 (2x+41) (21 x+4 (20 55° 60° KN=LM 36 = 9x 4 = x 115° (5y) 3y+13 3x-6 y (b (22) تصميم ما المعطيات الضرورية لتحديد ما إذا كانت الأجزاء المكونة للنمط أدناه متوازيات أضلاع؟ NJ = JL NJ = JL y + 15 = 3y - 7 190 الفصل 5 الأشكال الرباعية -2y= -22 y= 11 K الأضلاع المتقابلة في متطابقة تعريف تطابق القطع المستقيمة بالتعويض بالقسمة قطرا ينصف كل منهما الآخر تعريف تطابق القطع المستقيمة بالتعويض بالطرح بالقسمة وزارة التعليم Ministry of Education 2024-1446

أوجد مجموع قياسات الزوايا الداخلية لمضلع محدب عدد أضلاعه 22 ضلعا
قياس زاوية داخلية لمضلع منتظم 157.5 أوجد عدد أضلاعه
أوجد قيمة المتغير في كل مما يأتي
5-3 تمييز متوازي الأضلاع (ص 157-164) حدد ما إذا كان الشكل الرباعي في كل مما يأتي متوازي أضلاع أم لا. مثال 4 برر إجابتك. (23 (24 إذا كان 5 - 12 = TP = 4x + 2, QP = 6 - 2y, PS، 4 - PR = 6x ، فأوجد قيمتي x, y بحيث يكون QRST R P T S متوازي أضلاع. أوجد قيمة x بحيث تكون TP = PR وقيمة y بحيث تكون تعريف تطابق القطع المستقيمة بالتعويض بالطرح بالقسمة تعريف تطابق القطع المستقيمة بالتعويض بالطرح بالقسمة .QP = PS TP = PR 4x + 2 = 6x - 4 -2x=-6 x=3 (25) برهان اكتب برهانا ذا عمودين. المعطيات ABCD, AE = CF المطلوب : EBFD متوازي أضلاع. B F A E D QP = PS جبر أوجد قيمتي , x في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع. 6-2y= 12-5y x+4 55% (3x+6) (3y-4 (27 (26) 3y = 6 y=2 60 5y 3x-6 (y+12) (5x-2) مثال 5 جبر في المستطيل ABCD أدناه ، إذا كان ° (12 + mLADB = (Ax + 8), mZDBA = (6x، فأوجد قيمة x . B D C بما أن ABCD مستطيل، فإنّ 90 = MLABC. وبما أن الأضلاع المتقابلة في المستطيل متوازية، والزوايا المتبادلة داخليا بالنسبة للقطرين متطابقة، فإن DBC = ADB ، ومن تعريف التطابق 5-4 المستطيل ( ص 166-171) 28 جبر الشكل الرباعي RSTW مستطيل، إذا كان SW= (5x-20)in RZ = (2x+5)in، فأوجد x؟ W جبر: استعن بالمستطيل EFGH أدناه. E F K G . mZDBC = mZADB mZDBC+mZDBA = 90° mZADB +mZDBA = 90° H (29) إذا كان °57 = mZFEG، فأوجد mZGEH. (30) إذا كان °13 = mZHGE، فأوجد mLFGE. (31) إذا كان FK = 32 ft ، فأوجد EG. (32) أوجد mZHEF + mZEFG. مسلمة جمع الزوايا بالتعويض 90° = (12 + 4x + 8° + (6x) بالتعويض بالجمع بالطرح 90° 10x+20° 10x = 70° x = 7 بالقسمة الفصل 5 دليل الدراسة والمراجعة الت191يم Ministry of Education 2024-1446

أوجد قيمتي x, y بحيث يكون QRST متوازي أضلاع
في المستطيل أدناه أوجد قيمة x
دليل الدراسة والمراجعة مثال 6 الفصل 5 5-5 المعين والمربع (ص 179172 جبر: في المعين ABCD ، إذا كان 12 = EB = 9, AB "55 = mLABD، فأوجد كلا مما يأتي : AE (33 mZBDA (34 CE (35 mZACB (36 (37) شعار تتخذ شركة سيارات الشكل المجاور علامة تجارية لها. إذا كان شكل العلامة التجارية معينا، فما طول FJ؟ B A E 12.5cm G --- يتقاطع قطرا المعين QRST عند النقطة P. استعمل المعطيات لإيجاد المطلوب في كل مما يأتي: جبر إذا كان 9 - 12 = 1 + QT = x، فأوجد قيمة x . QT=TS QT = TS x + 7 = 2x - 9 - x = -16 x = 16 تعريف المعين تعريف تطابق القطع المستقيمة بالتعويض بالطرح بالقسمة إذا كان °76 = mLQTS، فأوجد mLTSP . بما أن TR تنصف QTS، فإن mLPTS = 1 mLQTS. لذلك "38= (76) 1 = mLPTS، وبما أن قطري المعين متعامدان، فإن °90 = mLTPS. هندسة إحداثية : حدد ما إذا كان QRST المعطاة إحداثيات رؤوسه في كل مما يأتي معينًا أو مستطيلا أو مربعًا. اكتب جميع 180° = mLPTS + mLTPS + mL TSP نظرية مجموع التسميات التي تنطبق عليه. ووضّح إجابتك. قياسات زوايا المثلث وزارة التعليم Ministry of Education 2024-1446 بالتعويض بالجمع بالطرح R Q 136 68 T نظرية مجموع قياسات الزوايا الداخلية للمضلع بالتعويض بالتبسيط بالطرح بالقسمة 38° + 90° + mLTSP = 180° 128° + mLTSP = 180° mLTSP = 52° Q(12, 0), R(6, -6), S(0, 0), T(6, 6) (38 Q(-2, 4), R(5, 6), S(12, 4), T(5, 2) (39 5-6 شبه المنحرف وشكل الطائرة الورقية (ص 180-188) أوجد القياس المطلوب في كل من السؤالين الآتيين: مثال 7 إذا كان QRST شكل طائرة ورقية، فأوجد mS. بما أن Q = S، فإن mZQ = mLS. اكتب معادلة وحلّها لإيجاد mZS. S mZQ+mZR+mZS+mZT= 360° mLS + 136° + mLS + 68" = 360" 2mZS + 204° = 360" 2mZS = 156" mZS = 78 23 W 112° X 23 mZZ (41 GH (40) F G 12 15x H (42) تصميم: استعن بقطعة البلاط المربعة الشكل المبينة جانبا في السؤالين الآتيين: a صف طريقة لتحديد ما إذا كانت أشكال شبه المنحرف الظاهرة في البلاطة متطابقة الساقين ؟ إذا كان محيط البلاطة 48in، ومحيط المربع الأحمر 16in، فما محيط أحد أشكال شبه المنحرف ؟ الفصل 5 الأشكال الرباعية 192

يتقاطع قطرا المعين QRST عند النقطة P استعمل المعطيات لإيجاد المطلوب في كل مما يأتي
إذا كان QRST أوجد m < s
لفصا 5 اختبار الفصل أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين: إذا كان CDFG على شكل طائرة ورقيّة، فأوجد القياس المطلوب في كل من السؤالين الآتيين C D mLD (13 G 67° 3 49° G GF (12 C F 4 D 1) السداسي (2) ذو 16 ضلعا 3) فن تصنع جُمانة إطارًا لتبسط عليه قطعة قماش وترسم عليها بألوان زيتية. ثبتت جمانة أربع قطع من الخشب بعضها ببعض واعتقدت أنها ستمثل مربعًا. a كيف يمكنها التحقق من أن الإطار مربع ؟ إذا كانت أبعاد الإطار كما في الشكل، فأوجد القياسات المجهولة. 2 ft y" الشكل الرباعي ABCD شبه منحرف متطابق الساقين. B A جبر: استعن بالمعين MNOP ، للإجابة عن الأسئلة الآتية: mZMRN (14 (15) إذا كان 12 = PR، فأوجد RN. (16) إذا كان 124 = mZPON، فأوجد mLPOM. M N R 17) إنشاءات تبني عائلة صالح ملحقا للمنزل، وتركت فتحة لنافذة جديدة. فإذا قاس صالح الأضلاع المتقابلة فوجدها متطابقة. وقاس القطرين فوجدهما متطابقين، فهل يمكنه القول: إن فتحة النافذة تمثل مستطيلا؟ وضح إجابتك. استعمل JKLM المبين جانبًا لإيجاد كل مما يأتي: 109° K M 6 L mJML (18 JK (19 mZKLM (20 D C (4) ما الزاوية التي تطابق C؟ (5) ما الضلع الذي يوازي AB؟ (6) ما القطعة المستقيمة التي تطابق AC؟ أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه في جبر: استعن بالمستطيل DEFG للإجابة عن الأسئلة الآتية: E D كل مما يأتي: 900° (7 2880° (9 1980° (8 5400° (10 11) اختيار من متعدد : إذا كان QRST متوازي أضلاع، فما قيمة x؟ R 14x - 34 34 12x - 8 G (21) إذا كان (2) - DF = 2 x + 5 - EG = 3 x، فأوجد EG. (22) إذا كان " (7) + mLEDF = (5x - 3) ", mLDFG = (3x، فأوجد mLEDF. (23) إذا كان 6 + (3) - (DE = 14 + 2x, GF = 4(x، فأوجد GF. حدد ما إذا كان الشكل الرباعي متوازي أضلاع أم لا في كل مما يأتي. الفصل 5 اختبار الفصلة ال193يم Ministry of Educat 2024-1446 (25 برر إجابتك. (24 S 13 C 11 A 14 D 12 B

الفصل 5 الإعداد للاختبارات تطبيق التعريفات والخصائص يتطلب حل كثير من المسائل الهندسية في الاختبارات تطبيق التعريفات والخصائص. استعمل هذه الصفحة والتي تليها للتدرّب على تطبيق التعريفات والخصائص عند حل أسئلة الهندسة ذات الإجابات المطولة. استراتيجيات تطبيق التعريفات والخصائص الخطوة | اقرأ نص السؤال بعناية. . حدّد المطلوب في المسألة. ا . ادرس الأشكال المعطاة في المسألة. . اسأل نفسك: ما خصائص هذا الشكل التي يمكنني تطبيقها لحل المسألة؟ الخطوة 2 حل المسألة. . حدّد التعريفات أو المفاهيم الهندسية التي يمكنك استعمالها لمساعدتك على إيجاد القيم المجهولة في ا . استعمل التعريفات وخصائص الأشكال لكتابة معادلة وحلها. المسألة. الخطوة 3 . تحقق من إجابتك. مثال اقرأ المسألة جيدًا، وحدّد المطلوب فيها . ثم استعمل المعطيات لحلها. يصنع خالد إطارًا خشبيا على شكل ثماني منتظم محيطه cm 288. ما طول كل لوح خشبي يشكل ضلعا للإطار ؟ ما الزاوية التي سيُقطع بها كل لوح عند طرفيه الخارجيين حتى تتلاءم الألواح بعضها مع بعض وتشكل الإطار؟ وضح إجابتك. a) طول كل ضلع من أضلاع الإطار أو طول كل لوح خشبي. 194 الخطوة 1: اقرأ المسألة بعناية، علمت أن الألواح ستشكل ثمانيا منتظما محيطه 288cm. والمطلوب إيجاد طول كل لوح . الفصل 5 الأشكال الرباعية وزارة التعليم Ministry of Education 2024-1446

الخطوة 1 تطبيق التعريفات والخصائص
الخطوة 2 تطبيق التعريفات والخصائص
الخطوة 3 تطبيق التعريفات والخصائص
اقرأ المسألة جيدا، وحدد المطلوب فيها. ثم استعمل المعطيات لحلها
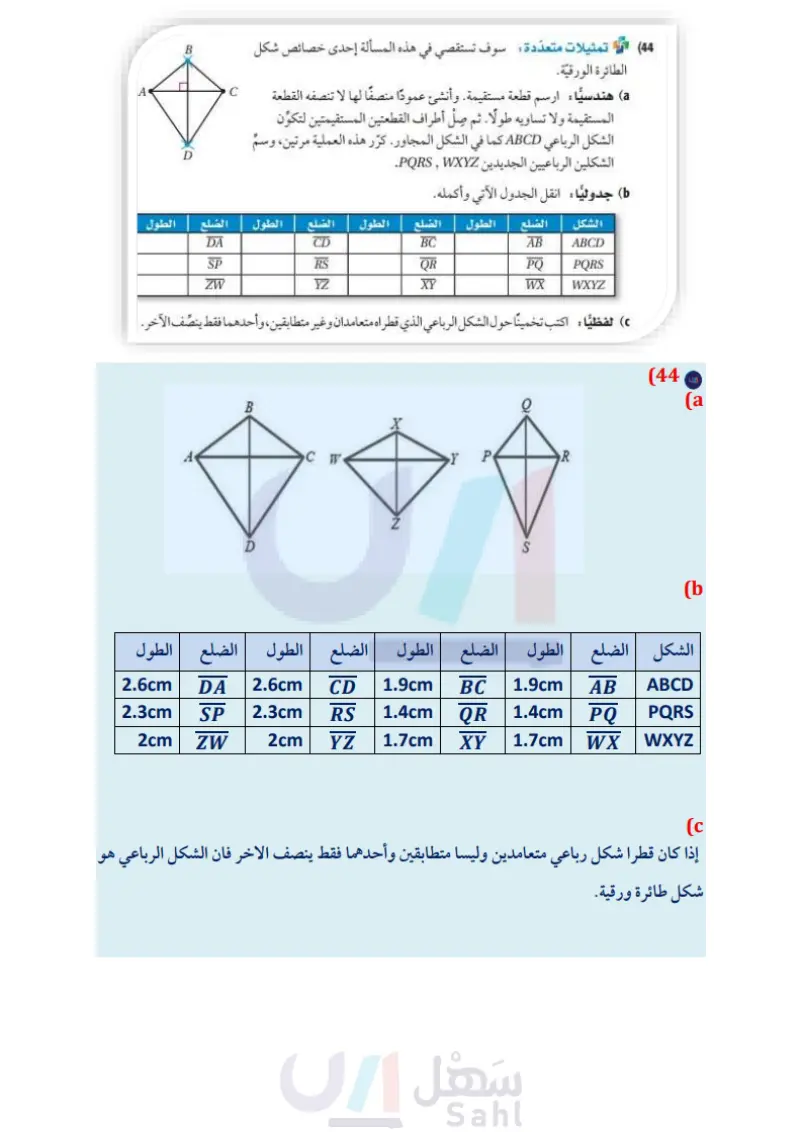
الخطوة 2: حل المسألة، لإيجاد طول كل لوح، اقسم المحيط على عدد الألواح. 2888 36 إذن طول كل لوح يجب أن يكون 36cm. الخطوة 3: تحقق من حلك بإيجاد محيط المضلع محيط المضلع المنتظم = عدد الأضلاع × طول الضلع الواحد 8x36cm = 288 cm قياس الزاوية التي سيقطع بها كل لوح عند طرفيه الخارجيين حتى تتلاءم الألواح وتشكل الإطار. الخطوة 1: المطلوب إيجاد قياس الزاوية التي ستقطع بها الألواح عند أطرافها حتى يتلاءم بعضها مع بعض تمامًا. الخطوة 2: حل المسألة، استعمل خاصية مجموع قياسات الزوايا الداخلية للمضلع المحدَّب لإيجاد قياس زاوية داخلية للثماني المنتظم. أوجد أولا المجموع 5 لقياسات الزوايا الداخلية. S (n-2) 180° = (8-2) 180° = 1080° إذن قياس الزاوية الداخلية للثّماني المنتظم يساوي 135 = 8 : 1080. وبما أنه سيُستعمل لوحان لتشكيل كل رأس للإطار، فإن كل طرف للألواح سيُقطع بزاوية قياسها 67.5 = 2 : 135. الخطوة 3: تحقق من حلك بالحل عكسيا أوجد عدد أضلاع المضلع المنتظم (n) الذي قياس زاويته الداخلية °135. (3) استعن بالتمثيل البياني أدناه في كل من السؤالين الآتيين: a) هل ينصف قطرا الشكل الرباعي RSTU كل منهما الآخر؟ استعمل صيغة المسافة بين نقطتين لتتحقق من إجابتك. ما نوع الشكل الرباعي RSTU؟ وضح إجابتك باستعمال خصائص هذا النوع من الأشكال الرباعية أو تعريفه. 4) ما مجموع قياسات الزوايا الخارجية للثماني المنتظم؟ الفصل 5 الإعداد للاختبارات ال195يم Ministry of Education 2024-1446 (n-2)-180° 135° = n 135°n = 180°n - 360° -45°n = - 360° n = 8 / تمارين ومسائل اقرأ كل مسألة مما يأتي، و ، وحدد المطلوب . ثم استعمل المعطيات لحلها، وبين خطوات حلك 1) RS قطعة متوسطة لشبه المنحرف MNOP. ما طول RS ؟ M. 10x + 3 N 9x - 1 R S D P 4x+7 /65" A x° (2) إذا كان AB || DC ، فأوجد قيمة x . C

حل المسألة لإيجاد طول كل لوح، اقسم المحيط على عدد الألواح
وزارة التعليم Ministry of Education 2024-1446 اختبار تراكمي الفصل 5 أسئلة الاختيار من متعدد اقرأ كل سؤال مما يأتي، ثم اكتب رمز الإجابة الصحيحة. 1) إذا كان 6 || ، فأي العبارات الآتية ليست صحيحة ؟ ما قياس كل زاوية داخلية في الخماسي المنتظم؟ B 120° C 96° A 135° D 108° B (5) الشكل الرباعي ABCD معين فيه 120 = mBCD، أوجد mDAC. 90° C 30° A 120° D 60° B 7/6 3/A a 22 = 25 C 2123 A 28 = 22 D 24 = 27 B (2) صنف المثلث أدناه تبعًا لقياسات زواياه. اختر المصطلح الأنسب. 60 60° 60° منفرج الزاوية قائم الزاوية (6) ما قيمة x في الشكل أدناه؟ 62' (5x+2)° 14 C 15 D 10 A S 12 B (1) DT, AE قطران للمستطيل DATE يتقاطعان في S. إذا كان 5 + AE = 0 T = x ، فما قيمة x؟ 15 C 10 D 35 A 25 B A حاد الزوايا B متطابق الزوايا (3) أوجد قيمة x في متوازي الأضلاع RSTU. T (4x+6)° 25 C 30 D (6x-54) R 12 A 18 B إرشادات للاختبار السؤال 3 استعمل خصائص متوازي الأضلاع لحل المسألة. كل زاويتين متقابلتين متطابقتان الفصل 5 الأشكال الرباعية 196

استعمل خصائص متوازي الاضلاع لحل المسألة كل زاويتين متقابلتين متطابقتان.
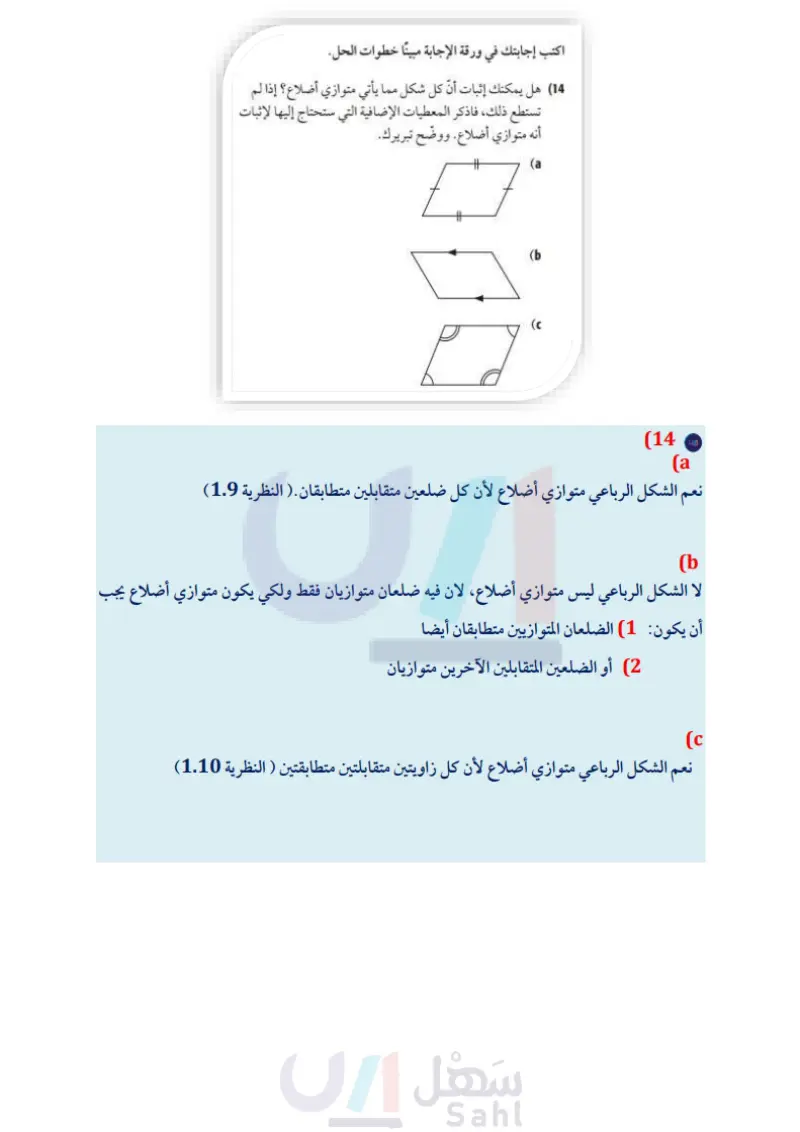
أسئلة ذات إجابات قصيرة اكتب إجابتك في ورقة الإجابة. 8) تشكل أعمدة خيمة رؤوس سداسي منتظم، ما قياس الزاوية المتكونة عند أي من أركان الخيمة؟ (12) أوجد قيمة x في الشكل أدناه وقرّب الإجابة إلى أقرب عُشر إن كان ذلك ضروريا. 6x + 4 5x+10 10x - 2 (13) ما إحداثيات مركز الدائرة التي تمر برؤوس المثلث أدناه؟ 3 У 9) ما إحداثيات الرأس الرابع لشبه المنحرف المتطابق الساقين LMNJ؟ بين خطوات الحل. IN M 00 10) ماذا نسمي متوازي الأضلاع إذا كان قطراه متعامدين ؟ وضح إجابتك. 11) حدد ما إذا كانت النتيجة صحيحة أم لا فيما يأتي اعتمادًا على المعطيات. فسر تبريرك. المعطيات: إذا كان العدد يقبل القسمة على 9، فإنّه يقبل القسمة على 3. العدد 144 يقبل القسمة على 9. النتيجة العدد 144 يقبل القسمة على 3. أسئلة ذات إجابات مطولة اكتب إجابتك في ورقة الإجابة مبينًا خطوات الحل. 14) هل يمكنك إثبات أن كل شكل مما يأتي متوازي أضلاع؟ إذا لم تستطع ذلك، فاذكر المعطيات الإضافية التي ستحتاج إليها لإثبات أنه متوازي أضلاع ووضح تبريرك. 14 13 12 11 10 9 8 7 6 5-3 مهارة سابقة 5-6 مهارة سابقة 5-1 5-6 5-5 5-4 مهارة سابقة الفصل 5 اختبار تراكمي ال197 Ministry of Educat 2024-1446 4 3 2 1 5-1 5-5 5-2 مهارة مهارة سابقة سابقة هل تحتاج إلى مساعدة إضافية ؟ إذا لم تستطع الإجابة عن السؤال فعد إلى الدرس..




 0
0 

 0
0