المعين والمربع - رياضيات 1-2 - أول ثانوي

F www.ien.edu.sa أضف إلى مطويتك وزارة التعليم Ministry of Education 2024-1446 G H J A B D N P \6 5 1 2. 8 4 R Q المعين والمربع Rhombus and Square الماذا؟ 5-5 فيما سبق درست تحديد ما إذا كان صمم فنان الألماسة المجاورة، بحيث تكونت من أنماط متكررة من تصمم الألماسات باستعمال أنماط متكررة من الأشكال الهندسية. إذا الشكل الرباعي متوازي أضلاع أو مستطيلا الدرس (4-5) والان - أتعرف خصائص المعين والمربع وأطبقها. . أحدد ما إذا كان الشكل الرباعي مستطيلا أو معينا أو مربعًا. المفردات: مثلثات وأشكال رباعية، كيف يمكن تحديد نوع الأشكال الرباعية المحددة باللون الأحمر في الألماسة؟ خصائص المعين والمربع المعين هو متوازي أضلاع جميع أ أضلاعه متطابقة. وللمعين جميع خصائص متوازي الأضلاع علاوة على الخاصيتين الواردتين في النظريتين الآتيتين : نظريات قطرا المعين 5.15 إذا كان متوازي أضلاع معيّنا، فإن قطريه متعامدان. مثال : إذا كان ABCD معيّنا، فإن . AC 1 BD 5.16 إذا كان متوازي أضلاع معيّنا فإن كل قطر فيه ينصف كلا من الزاويتين اللتين يصل بين رأسيهما. مثال: إذا كان NPQR معينا، فإن Z1 Z2, Z3 Z4, 25 = 26, 27 = 28 سوف تبرهن النظرية 5.16 في السؤال 28 برهان نظرية 5.15 أكتب برهانا حرا للنظرية 5.15 المعطيات ABCD معين المطلوب: AC IBD البرهان بما أن ABCD معيّن، فإن AB = BC بحسب التعريف. B P C D وبما أن المعيّن متوازي ،أضلاع، وقطري متوازي الأضلاع ينصف كل منهما الآخر، فإنّ BD ينصف AC عند P؛ لذا فإن AP = PC . وكذلك BP = BP بحسب خاصية الانعكاس؛ إذن AAPB = ACPB بحسب SSS وبما أن العناصر المتناظرة في المثلثات المتطابقة تكون متطابقة، فإن LAPB = LCPB. وكذلك APB ,CPB متجاورتان على مستقيم، والزاويتان المتطابقتان المتجاورتان على مستقيم تكونان قائمتين. وبما أن APB قائمة، فإن AC 1 BD بحسب تعريف المستقيمين المتعامدين. الفصل 5 الأشكال الرباعية المعين rhombus المربع square 172

F G K эн مثال 1 استعمال خصائص المعين استعن بالمعين FGHJ المبين جانبًا. a) إذا كان 82 = mLFJH، فأوجد mLKHJ. بما أن FGHJ معيّن، فإن القطر JG ينصف LFJH. لذا فإن mZKJH = = mZFJH. إذن "41 = (82) { = m_KJH وبما أن قطري المعين متعامدان، فإنّ 90 = mJKH بحسب تعريف المستقيمين المتعامدين. نظرية مجموع قياسات زوايا المثلث بالتعويض بالتبسيط بطرح 131 من كلا الطرفين A B D mZKJH+mZJKH+mZKHJ = 180° 41° + 90° + mZKHJ = 180° 131° + mZKHJ = 180° mZKHJ = 49° جبر إذا كان 2 - GH = x + 19 JH = 5x ، فأوجد قيمة x. GH = JH GH = JH x+9=5r 2 9 = 4x - 2 11 = 4x 2.75 = x تعريف المعين تعريف تطابق القطع المستقيمة بالتعويض بطرح x من كلا الطرفين بجمع 2 لكلا الطرفين بقسمة كلا الطرفين على 4 تحقق من فهمك استعن بالمعين FGHJ أعلاه. 1) إذا كان 13 = FK = 5, F، فأوجد KJ 18) جبر إذا كان " (5) - (9) = mJFK = (6y + (7)", mZKFG، فأوجد قيمة y. إرشادات للدراسة المربع هو متوازي أضلاع جميع أضلاعه متطابقة وجميع زواياه قوائم. تذكّر أن متوازي الأضلاع الذي زواياه الأربع قوائم يكون مستطيلا، ومتوازي الأضلاع الذي أضلاعه الأربعة المربع والمعين متطابقة يكون معيّنا ؛ لذا فعندما يكون متوازي الأضلاع معيّنا وإحدى زواياه قائمة فإنه يكون كل مربع معين ولكن مربعا أيضًا، وعليه فإن المربع هو متوازي أضلاع ومستطيل ومعين. ليس كل معين مربعا وكل مربع مستطيل ويلخص شكل من الآتي العلاقة بين متوازي الأضلاع والمعين والمربع والمستطيل. وليس كل مستطيل مربعا. ملخص المفهوم متوازي الأضلاع متوازي الأضلاع الأضلاع المتقابلة متوازية ) C المربع ABCD أضف إلى طويتك المستطيل المعين المربع ( الزوايا الأربع قوائم) الأضلاع الأربعة متطابقة) الدرس - المعين والمربع ال 173يم Ministry of Edu 2024-1446

تنبيه ! أخطاء شائعة يخطئ البعض فيستعمل النظريات 5.17, 5.18, 5.19 مع أي شكل رباعي وهذا غير صحيح؛ لأن هذه النظريات تكون صحيحة فقط إذا كان الشكل الرباعي متوازي أضلاع. إرشادات للدراسة المثلثات المتطابقة بما أن للمعين أربعة أضلاع متطابقة، فإن كلا من قطريه يقسمه إلى مثلثين متطابقي الضلعين ومتطابقين وإذا رسم القطران جميع خصائص متوازي الأضلاع والمستطيل والمعين تنطبق على المربع فمثلا قطرا المربع ينصف كل منهما الآخر (متوازي أضلاع، وهما متطابقان (مستطيل)، ومتعامدان (معين). إثبات أن الشكل الرباعي معين أو مربع تُحدد النظريات الآتية الشروط الكافية للمعين والمربع. نظريات الشروط الكافية للمعين والمربع 5.17 إذا كان قطرا متوازي أضلاع متعامدين فإنه معيّن (عكس النظرية (5.15) مثال: إذا كان JKLM متوازي أضلاع، وكان JL LKM ، فإن JKLM معين. K L 5.18 إذا نصف قطر متوازي أضلاع كلا من الزاويتين اللتين يصل بين رأسيهما، فإن متوازي الأضلاع يكون معينا. (عكس النظرية 5.16) مثال : إذا كان WXYZ متوازي أضلاع، وكانت 24 = 3 ,2 = 1، 2546,47 48 gi فإن DWXYZ معين. 5.19 إذا كان ضلعان متتاليان في متوازي الأضلاع متطابقين فإنه معين. مثال: إذا كان ABCD متوازي أضلاع، وكان AB = BC ، فإن ABCD معين. 5.20 إذا كان الشكل الرباعي مستطيلا ومعينا فإنه مربع. B M أضف إلى مطويتك 1 W 5 8 x سوف تبرهن النظريات 5.17 إلى 5.20 في الأسئلة 32-29 على الترتيب. يمكنك استعمال خصائص المعيّن والمربع في البراهين. مثال 2 استعمال خصائص المعين والمربع في البراهين اكتب برهانا حرا. المعطيات JKLM متوازي أضلاع AJKL متطابق الضلعين. المطلوب JKLM معين. برهان حر L M C 3 A P K D فإنهما يقسمان المعين بما أن AJKL متطابق الضلعين، فإن KL = JK بحسب التعريف، وهذان الضلعان متتاليان في متوازي إلى أربعة مثلثات قائمة ومتطابقة. الأضلاع JKLM ، لذا وبحسب النظرية 1.19، يكون JKLM معيناً. 174 الفصل 5 الأشكال الرباعية تحقق من فهمك (2) اكتب برهانا حرا. المعطيات SQ عمود منصف لـ PR PR عمود منصف لـ SQ . ARMS متطابق الضلعين. المطلوب PQRS مربع. S M Q R وزارة التعليم Ministry of Education 2024-1446

مثال 3 من واقع الحياة استعمال المعين والمربع علم الآثار: مفتاح الكشف الناجح عن الآثار هو وضع خريطة دقيقة لموقع البحث. كيف يمكن لعالم الآثار في الصورة أدناه أن يتحقق من أن منطقة بحثه هي مربع طول ضلعه m 1 مستعملا الحبل وشريط القياس فقط ؟ الربط مع الحياة علم الآثار هو دراسة أعمال الإنسان في العصور القديمة كي يزودنا بمعلومات حول حياته ونشاطاته. وساعد اكتشاف الإنسان للكتابة منذ 5000 عام تقريبًا على فهم أسرار أزمنة ما بعد هذا التاريخ m m طول كل من أضلاع الشكل الرباعي ABCD يساوي 1m. وبما أن كل ضلعين متقابلين متطابقان، فإنّ ABCD متوازي أضلاع. وبما أن أضلاع ABCD المتتالية متطابقة فإنّه معين. وإذا استطاع عالم الآثار بيان أن ABCD مستطيل أيضًا فإنّه بحسب النظرية 5.20، يكون مربعا . 1 m 1 m 1 m إذا كان قطرا متوازي الأضلاع متطابقين فإنّه مستطيل؛ لذا يمكن لعالم الآثار استعمال الحبل لقياس طولي القطرين، فإذا وجدهما متساويين، فإن ABCD يكون مربعًا. تحقق من فهمك 3) خياطة: خاطت كوثر غطاء طاولة باستعمال قطع ملونة من القماش كما في الرسم المجاور. A رسمت کوثر قطري كل من القطع الصفراء فوجدت أنهما متعامدان، هل يمكنها استنتاج أن كل قطعة صفراء معين؟ وضح إجابتك. إذا كانت الزوايا الأربع للقطعة الخضراء متساوية القياس، والضلعان الأيسر والسفلي متساويي الطول، فهل يمكنها استنتاج أن القطعة الخضراء مربع؟ وضح إجابتك. استعملت الهندسة الإحداثية سابقا لتصنيف المثلثات. ويمكن استعمال الهندسة الإحداثية لتصنيف الأشكال الرباعية أيضًا. الدرس - المعين والمربع ال175 Ministry of Edu 2024-1446

إرشادات للدراسة تمثيل الشكل بيانيا : عند تحليل شكل رباعي باستعمال الهندسة الإحداثية، مثله بيانيا لمساعدتك على وضع تخمين، ثم تحقق من تخمينك جبريًا. مثال 4 تصنيف الأشكال الرباعية باستعمال الهندسة الإحداثية هندسة إحداثية: حدد ما إذا كان JKLM الذي إحداثيات رؤوسه (2) ، 4 ,0)، (92) (24) معيّنا أو مستطيلا أو مربعًا. اكتب جميع التسميات التي تنطبق عليه. وضّح إجابتك. افهم : المعطيات: JKLM إحداثيات رؤوسه L(9, 2). K(0, 4) (-7,-2) .M (2,-4) المطلوب إثبات أن JKLM هو معين أو مستطيل أو مربع. خطط : عين الرؤوس على المستوى الإحداثي وصل بينها. K يظهر من الرسم أن أضلاع JKLM متطابقة. ولكن زواياه ليست قوائم؛ لذا يبدو أنه معين وليس مربعًا أو مستطيلا. إذا كان قطرا متوازي الأضلاع متطابقين فإنّه مستطيل. وإذا كانا متعامدين فإنه معين. وإذا كانا متطابقين ومتعامدين فإنه مستطيل ومعين؛ أي أنه مربع. حل: أولا: استعمل صيغة المسافة بين نقطتين للمقارنة بين طولي القطرين. 176 الفصل 5 الأشكال الرباعية KM (2-0)2 + (-4-4)²= √√68 = 2√√17 JL = V[9 - (7)]2 + [2 - (2) 2 = 272 = 417 بما أن 417 + 217 ، فإن القطرين ليسا متطابقين؛ لذا JKLM ليس مستطيلا. وبما أنه ليس مستطيلا فإنه ليس مربعا أيضًا. ثانيا: استعمل صيغة الميل لتحديد ما إذا كان القطران متعامدين . میل KM : -4-4 2-0 2-(-2) -=-4 میل IL : 1 = 1 9-(-7) وبما أن حاصل ضرب الميلين يساوي 1-، فإن القطرين متعامدان؛ لذا فإن JKLM معين. تحقق 85 JK = V[4 - (2)]2 + [0 - (-7)]2 = ' KL = √√(9-0)² + (2 – 4)² = √85 لذا فإن JKLM معين بحسب النظرية 1.20 . ميل JK : - 4-(-2) 0-(-7) = ، وميل. وبما أن حاصل ضرب هذين الميلين لا يساوي 1-، فإن الضلعين المتتاليين JK و KL غیر متعامدين؛ لذا فإن JKL ليست قائمة؛ إذن JKLM ليس مستطيلا ولا مربعا. ✓ تحقق من فهمك (4) حدد ما إذا كان JKLM الذي إحداثيات رؤوسه - 6 )K(8, 11), L1 ,0 ,5) ، معيّنا أو مستطيلا أو مربعا ؟ اكتب جميع التسميات التي تنطبق عليه. وضح إجابتك. وزارة التعليم Ministry of Education 2024-1446

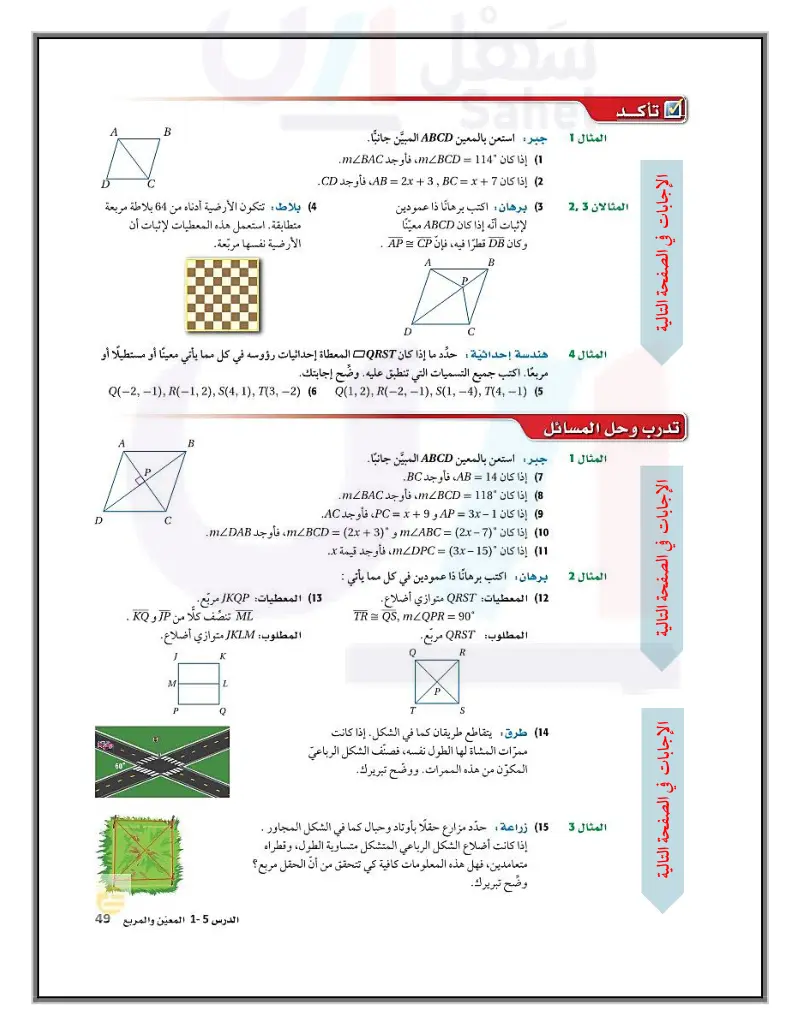
المثال 1 جبر: استعن بالمعين ABCD المبين جانبا. (1) إذا كان 114 = mBCD، فأوجد mZBAC. إذا كان + AB = 2x + 3 = x، فأوجد CD. المثالان 23 (3) برهان اكتب برهانا ذا عمودين لإثبات أنه إذا كان ABCD معيّنا وكان DB قطرًا فيه، فإن AP = CP A B بلاط : تتكون الأرضية أدناه من 64 بلاطة مربعة متطابقة. استعمل هذه المعطيات لإثبات أن الأرضية نفسها مربعة. B P C هندسة إحداثية: حدد ما إذا كان QRST المعطاة إحداثيات رؤوسه في كل مما يأتي معينًا أو مستطيلا أو مربعًا. اكتب جميع التسميات التي تنطبق عليه. وضح إجابتك. Q(-2, -1), R(-1, 2), S(4, 1), T(3,-2) (6 Q(1, 2), R(-2, -1), S(1, -4), T(4, -1) (5 المثال 4 تدرب وحل المسائل المثال 1 جبر: استعن بالمعين ABCD المبين جانبًا. (7) إذا كان 14 = AB، فأوجد BC. 8 إذا كان 118 = mBCD، فأوجد mBAC. (9) إذا كان 1 - AP = 3 x و 9 + PC = x ، فأوجد AC. (10) إذا كان 7 - mABC = (2x و ° (3) + mBCD = (2x، فأوجد mDAB. (11) إذا كان " (15) - mLDPC = (3x، فأوجد قيمة x المثال 2 برهان اكتب برهانا ذا عمودين في كل مما يأتي : (12) المعطيات QRST متوازي أضلاع TR QS, mZQPR = 90° المطلوب QRST مربع 13) المعطيات JKQP مربع .. B P A D C ML تنصف كلا من JP و KQ. المطلوب: JKLM متوازي أضلاع J K M L P Q الدرس المعين والمربع ال177يم Ministry of Educ 2024-1446 R T S 14 طرق : يتقاطع طريقان كما في الشكل. إذا كانت ممرات المشاة لها الطول نفسه، فصنف الشكل الرباعي المكوّن من هذه الممرات. ووضح تبريرك. المثال 3 15) زراعة حدّد مزارع حقلًا بأوتاد وحبال كما في الشكل المجاور . إذا كانت أضلاع الشكل الرباعي المتشكل متساوية الطول، وقطراه متعامدين فهل هذه المعلومات كافية كي تتحقق من أن الحقل مربع؟ وضّح تبريرك.

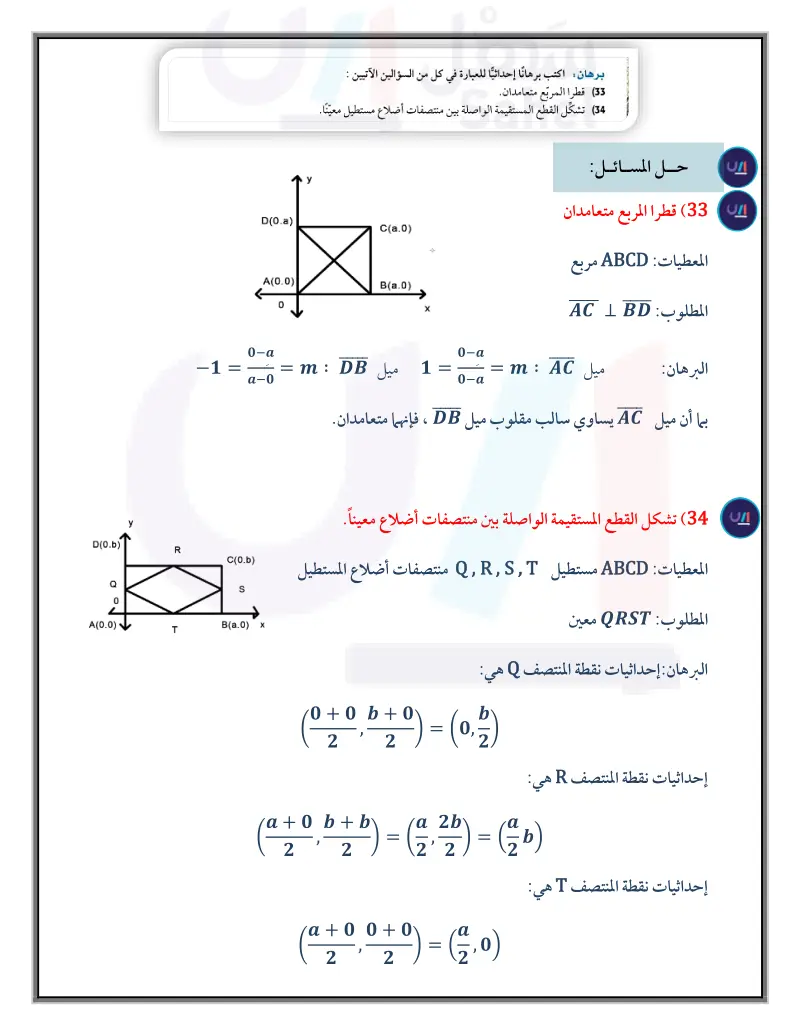
المثال 4 هندسة إحداثية: حدد ما إذا كان IKLM المعطاة إحداثيات رؤوسه في كل مما يأتي معينًا أو مستطيلا أو مربعا. اكتب جميع التسميات التي تنطبق عليه. ووضّح إجابتك. J(-3,-2), K(2,-2), L(5, 2), M(0, 2) (17 J(-4, -1), K(1, −1), L(4, 3), M(-1,3) (16 J(-2, -1), K(-4, 3), L(1, 5), M(3, 1) (18 A J(-1, 1), K(4, 1), L(4, 6), M(-1, 6) (19 P B في المعين ABCD ، إذا كان 24 = PB = 12, AB = 15, ABD، : فأوجد كلا مما يأتي : CP (21 D C mZACB (23 W T Z B N A D * X AP (20 mZBDA (22 في المربع WXYZ، إذا كان 3 = WT، فأوجد كلًا مما يأتي : XY (25) mZWYX (27 ZX (24 mZWTZ (26 برهان اكتب برهانا حرًّا لكل مما يأتي : (28) النظرية 5.16 (29) النظرية 5.17 (30) النظرية 5.18 (32) النظرية 5.20 C (31) النظرية 5.19 الربط مع الحياة الفسيفساء صور تشكل باستعمال أنماط من أحجار أو زجاج أو قرميد أو أي مواد أخرى. والفسيفساء في الصورة أعلاه فسيفساء إغريقية قديمة من الصخر البلوري (الكوارتز). استعمل الإغريق قطعا صغيرة أو أشكالا منتظمة من المواد منذ 200 سنة قبل الميلاد بدلا من الصخر البلوري في أعمال الفسيفساء. برهان اكتب برهانًا إحداثيا للعبارة في كل من السؤالين الآتيين : 33) قطرا المربع متعامدان. (34) تشكل القطع المستقيمة الواصلة بين منتصفات أضلاع مستطيل معينًا. (35) تصميم : يتكون نمط الفسيفساء المبين جانبا من قطع ثمانية منتظمة وأخرى رباعية. صنف الأشكال الرباعية في ا ووضّح تبريرك. النمط، (36) تمثيلات متعدّدة : سوف تستقصي في هذه المسألة إحدى خصائص شكل الطائرة الورقية، وهو شكل رباعي يتكون من زوجين متمايزين من الأضلاع المتجاورة والمتطابقة. a) هندسيا : ارسم قطعة مستقيمةٌ، ثم افتح الفرجار وثبته عند أحد طرفيها وارسم قوسًا فوقها، ومن دون تغيير فتحة الفرجار، ثبت رأس الفرجار عند الطرف الآخر للقطعة المستقيمة، وارسم قوسًا يقطع القوس السابق. غير فتحة الفرجار وارسم قوسين أسفل القطعة المستقيمة كما فعلت سابقا. استعمل المسطرة وصل بين طرفي القطعة والأقواس، وسينتج لك شكل طائرة ورقية سمّها ABCD . ثم كرّر ذلك مرتين، وسمّ شكلي الطائرتين الورقيتين، PQRS WXYZ، ثم ارسم قطري كل منهما، ولتكن نقطة تقاطع قطري كل منها N. (6) جدوليا : استعمل مسطرة لقياس المسافة من N إلى كل رأس. وسجل النتائج في جدول على النحو الآتي. الشكل على القطر الأقصر المسافة من N إلى كل رأس المسافة من N إلى كل رأس على القطر الأطول ABCD PQRS WXYZ لفظيا : اكتب تخمينا حول قطري شكل الطائرة الورقية. وزارة التعليم Ministry of Education 2024-1446 الفصل 5 الأشكال الرباعية 178

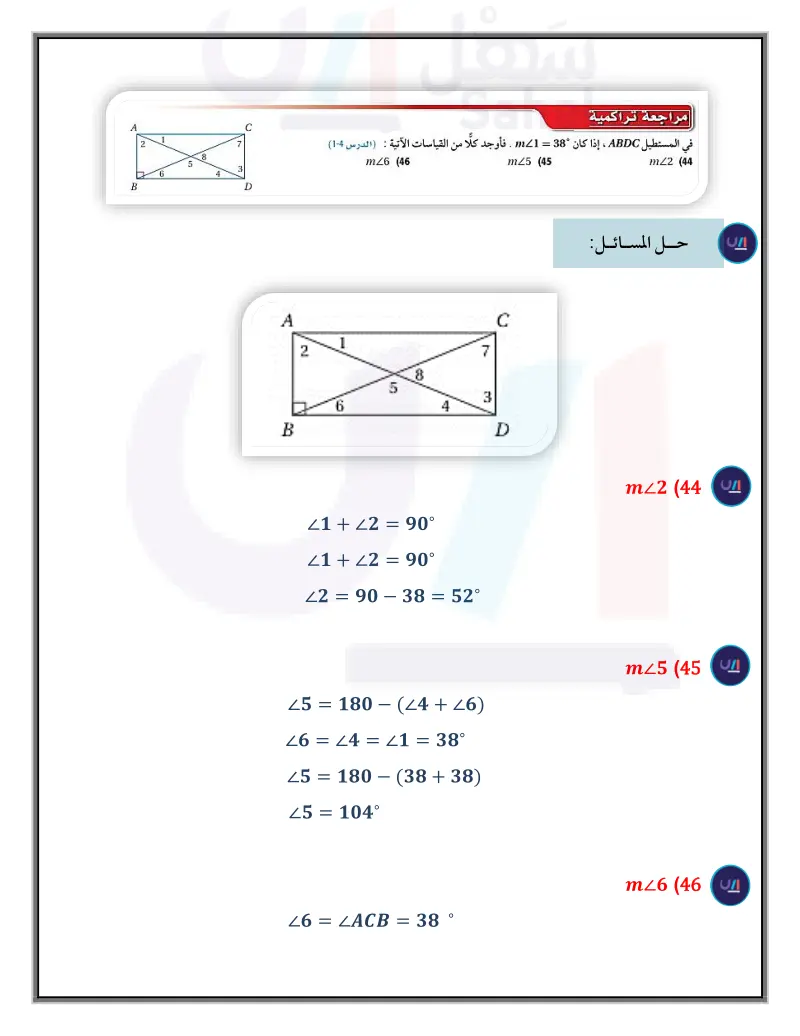
تدريب على اختبار مسائل مهارات التفكير العليا 37 اكتشف الخطأ في الشكل الرباعي SRQP المبين جانبا، PR = QS. قال محمد: إن الشكل مربع. بينما قال إبراهيم: إنه معين. هل أي منهما على صواب؟ وضح تبريرك. (38) تبرير: حدد ما إذا كانت العبارة الآتية صحيحة أم خطأ؟ ثم اكتب عكسها ومعكوسها ومعاكسها الإيجابي، وحدد قيمة الصواب لكل منها. وضح تبريرك. إذا كان الشكل الرباعي مربعا، فإنّه مستطيل. 39) تحد: مساحة المربع ABCD المجاور تساوي 36 وحدة مربعة. ومساحة AEBF تساوي 20 وحدة مربعة. إذا كانت EB 1 BF ، وطول AE يساوي وحدتين، فأوجد طول CF . (40) مسألة مفتوحة أوجد إحداثيات رؤوس مربع قطراه محتویان في المستقيمين 6 + y = x, y = x. وضح تبريرك. (41) اكتب قارن بين جميع خصائص الأشكال الرباعية الآتية : متوازي الأضلاع، المستطيل، المعين، المربع. (42) في المعين JKLM ، إذا كان 8 = JK = 10 ، CK ، فأوجد JC Q S R A B E D C F (43) جبر: ما قيمة كل من , x بحيث يكون ABCD متوازي أضلاع؟ A 17, A 13 B D 5x + y C 2 1 B 6 8 4 x = 3, y = 2 A x = ,y = -1 B M 13x-3y x= 2, y = 3 C D x = 3, y = - 1 D (49 4.5 4.5 8C 10 D 4 A 6 B مراجعة تراكمية في المستطيل ABDC ، إذا كان 38 = m1 . فأوجد كلًا من القياسات الآتية : (الدرس 4-5) mZ6 (46 mZ5 (45 mz2 (44 حدد ما إذا كان الشكل الرباعي في كل مما يأتي متوازي أضلاع أم لا. برر إجابتك (الدرس 3-5) (48 (47 60° 120° (50) قياسات قال :مروان إن الحديقة الخلفية لمنزله على شكل مثلث أطوال أضلاعه ft 3 ft, ft 22 فهل ترى أن هذه القياسات صحيحة ؟ وضح تبريرك. (مهارة سابقة) (12x + 6-8x+7)=9 (53 { (10x + 6x + 2) = 7 (52 الدرس - المعين والمربع ال179يم Ministry of Educ 2024-1446 استعد للدرس اللاحق حل كل معادلة مما يأتي : (5x+7x-1)=11.5 (51