توصيف البيانات عن طريق الإحصاءات الجزء الأول - صناعة القرار في الأعمال - ثاني ثانوي
الجزء الأول
الفصل1: تحديد المشكلات وتعريفها
الفصل2: حل المشكلة
الفصل3: التفكير الناقد
الفصل4: اتخاذ القرار وحل المشكلات ضمن مجموعة
الفصل5: أدوات دعم القرار
الجزء الثاني
الفصل6: خطوات اتخاذ القرار في المنظمات
الفصل7: إدارة الفرق لدعم القرارات في المنظمات
الفصل8: التواصل التنظيمي وصنع القرارات
الفصل9: استخدام البيانات لدعم عملية اتخاذ القرار
الجزء الثالث
الفصل10: أساسيات نظام دعم القرار
الفصل11: استخدام أداة سولفر في برنامج مايكروسوفت إكسل
الفصل12: مشروع إنتاج السيارات
الفصل13: مشروع منتجع التزلج
الفصل14: مشروع السيارة الكهربائية
الفصل15: مشروع شركة الطيران
310 الدرس 4 الفصل 9 رابط الدرس الرق www.ien.edu.sa توصيف البيانات عن طريق الإحصاءات ( الجزء الأول ) 1-4 أهمية الإحصاء The importance of statistics || يُعتبر البشر غير منطقيين أحيانًا في القرارات التي يتخذونها ؛ نحن لا نقول هذا من باب الانتقاد وإنما من باب إبداء الملحوظة حول الطريقة التي يميل إليها العقل لمعالجة البيانات والمعلومات التي تصله. فمثلا، لقد بينت الدراسات مبالغة الناس أحيانًا في تقدير قدرة التمارين الرياضية على استهلاك ما نأكله. وفي مثل هذه الحالة يتناول الناس كمية مأكولات أكبر من الكمية التي يمكنهم استهلاكها بالتمارين الرياضية التي يمارسونها ، بل بدأ بعض الباحثين يتساءلون إذا كان مجرد التفكير في التمارين الرياضية يؤدي إلى تناول كمية أكبر من الطعام بمجرد التفكير في التمارين الرياضية، يجعلني أتناول مزيدًا من الطعام فالنشاط الجسدي سيعوض عن السعرات الحرارية المكتسبة". بناءً عليه، أجرى الباحثون تجربة وزّعوا فيها على المشاركين وجبات خفيفة كمكافأة على المشاركة. وبموجب هذه التجربة، طلبوا من المشاركين قراءة مقال قصير والإجابة من بعده عن بعض الأسئلة . قرأت المجموعة الأولى من المشاركين مقالا لا علاقة له بالتمارين الرياضية، عنوانه "ضبط السعرات الحرارية أما المجموعة الثانية فقرأت مقالًا يتحدث عن الإصغاء إلى الموسيقى خلال نزهة على الأقدام مدتها 30 دقيقة، عنوانه "المرح مع السعرات الحرارية" فيما المجموعة الثالثة قرأت مقالا عن التمارين الرياضية الشاقة عنوانه " الرياضة والسعرات الحرارية" في الشكل "9-3". ୨ أعطي المشاركون كيسين فيهما نوعان من الحلويات والوجبات الخفيفة اللذيذة، وطلب منهم أن يأكلوا ما طاب لهم من الكيسين . وبعد تناول المشاركين ما حلا لهم ، تم وزن الكيسين حتى يحدد الباحثون عدد السعرات الحرارية التي استهلكت، ومن ثم استخدموا عدد السعرات الحرارية الذي استهلكته كلّ مجموعة ليرسموا المخطّط النقطي المبين بالشكل التالي. يتضح من هذا المخطّط اختلاف عدد السعرات الحرارية المستهلكة من شخص إلى شخص، مع كونه أعلى بكثير عند أولئك الأشخاص الذين قرؤوا عن التمارين الرياضية مقارنة بالمشاركين الذين شاركوا بالمجموعة الأولى التي قرأت مقالا لا علاقة له بالرياضة. حتى نبيّن المقارنة بشكل أوضح، من الأفضل لنا تلخيص النتائج باستخدام الأرقام. الشكل "9 - 3 : مخطّط نقطي للسعرات الحرارية ضبط السعرات الحرارية المرح مع السعرات الحرارية : 300 400 500 600 700 800 900 الرياضة والسعرات الحرارية الفصل 9 السعرات الحرارية وزارة التعليم Ministry of Education 2024-1446

توصيف البيانات عن طريق الإحصاءات
24 المقاييس الرقمية الموجزة Numerical summary measures بعد ذلك سننظر في أصول احتساب المقاييس الرقمية الموجزة التي تصف لنا النقطة الوسطى ومدى الاختلاف في مجموعات البيانات. لمحة سريعة • لتوصيف البيانات الرقمية بشكل واضح نحدد بالعادة قيمة لها مكانة تمثيلية لمجموعة مقاييس النزعة البيانات تطلعنا بشكل تقريبي على نقطة تموضع أو تمركز البيانات على خط الأرقام، ومن هنا تسميتها مقاييس النزعة المركزية Measure of center. المقياسان الأكثر استخدامًا المركزية هي مقاييس مفيدة لغالبية الأمور التي نقيسها، وذلك بسبب ميل البيانات إلى التجمع حول نقطة مركزية. هما الوسط والوسيط. تعريف مقياس النزعة المركزية Measure of center مقياس موجز يسعى إلى وصف مجموعة كاملة من البيانات من خلال قيمة واحدة تمثل وسط أو مركز توزيعه. وهو • الوسط Mean في مجموعة بيانات رقمية هو المتوسط الحسابي الذي نعرفه جميعنا: وبذلك فمقاييس يُقاس بجمع قيم مختلف عناصر مجموعة البيانات وقسمتها على عدد العناصر. من المفيد النزعة المركزية تحديد المتغيّر الذي تصفه هذه الأرقام، لعدد العناصر في مجموعة البيانات، ولكل عنصر تخبرنا الكثير منفرد وفق الآتي: عن البيانات من خلال رقم واحد بسيط. = المتغيّر الذي يُدرس n = عدد العناصر في مجموعة البيانات (حجم العينة) x1 = قيمة العنصر الأول في مجموعة البيانات x2 = قيمة العنصر الثاني في مجموعة البيانات xn = قيمة آخر عنصر في مجموعة البيانات = إذا كانت عينتنا مثلًا، تتألف من (4) عناصر لمتغيّر (x) = الوقت اللازم لتنفيذ حجز n x4=5.7 x3=6.6 x2 = 7.3 فندقي (بالدقائق): x1 = 5.9 لاحظ غياب علاقة الرقم الموجود بمحاذاة الرمز "n" بقيمة العنصر ، ففي هذا المثل، "x1" وهو العنصر الأول في مجموعة البيانات ليس بالضرورة أصغر العناصر، فيما (xn) يمثل آخر عنصر في مجموعة البيانات من دون وجوب كونه أكبرها. يمكن تمثيل عملية جمع قيم مختلف العناصر x1 + x2 + ... + x) كالآتي xn ... + 2 ( 1 ) أو بمختصرها الذي يُمثل بالحرف اليوناني (٤) ، إذ يعني (٤) مجموع قيم مختلف عناصر مجموعة البيانات قيد الدراسة. استخدام البيانات لدعم عملية اتخاذ القران الـ311 Ministry of Education 2024-1446

مقاييس النزعة المركزية هي مقاييس مفيدة لغالبية الأمور التي نقيسها
تعريف الوسط أو المتوسط الحسابي Mean هو المتوسط الحسابي لعيّنة تتألف من عدة عناصر رقمية ،، = X X2 لک يمثل بحرف (x) ، معادلته الحسابية كالآتي: مجموع قيم مجمل العناصر الموجودة في العينة عدد العناصر الموجودة في العينة Ex 1+ X, + X2 + ... + X n n الخط الوسيط الذي تراه على الطريق العام هو الخط الذي يقسم الطريق العام إلى شطرين. أما في مجموعة البيانات الرقمية، فيلعب الوسيط الدور نفسه. فمثلا في ترتيب القيم من أصغرها إلى أكبرها ، يكون الوسيط Median هو القيمة التي تقع في وسط المجموعة، وهو يقسمها إلى شطرين متساويين من حيث عدد العناصر. • تختلف عملية تحديد الوسيط بعض الشيء بحسب حجم العينة ( عدد العناصر في العينة)، أي بحسب إذا كانت العيّنة زوجية أو فردية. عندما يكون عدد العناصر في العينة عددًا فرديًّا (5) مثلا ) ، يكون الوسيط هو القيمة التي تقع في وسط العيّنة. أما في حال كان عدد العناصر في العيّنة زوجيًّا (6) مثلا) فسنجد رقمين وسطيين في القائمة المرتبة بالتسلسل، ويجب احتساب متوسط هاتين القيمتين لنحصل على الوسيط في هذه العينة. تعريف وسيط العينة Median نحصل على الوسيط أولا بترتيب عناصر العينة من أصغرها إلى أكبرها ( ونضع القيمة المتكررة على هذه القائمة ولا نحذفها، وهكذا يكون كل عنصر من عناصر العينة موجودًا على القائمة ) . وسيط العينة = القيمة الوسطى في حال كان حجم العينة رقماً فرديًّا، أو متوسط القيمتين المتوسطتين في حال كان حجم العينة رقما زوجيًّا. و متى يجب استخدام المتوسط الحسابي ومتى عليك اختيار الوسيط لتوصيف مجموعات البيانات؟ أنظر إلى المثال التالي تضع إحدى المنظمات على موقعها الإلكتروني معلومات عن منتجات حتى تتيح لعملائها الوصول إلى هذه المعلومات. نبيّن في ما يلي خلاصة تقرير يُظهر عدد الزيارات لكل صفحة منتج خلال الأسبوع الماضي. حجم عيّنة الزيارات إلى الموقع هو w 40 = n ، وهو رقم زوجي. بترتيب البيانات من أصغرها إلى أكبرها نحصل على القائمة التالية ( مع إبراز القيمتين الوسطيتين) : 0000003444 5 5 7 7 8 12 12 88 13 13 13 14 14 16 18 20 19 19 20 21 23 22 36 26 36 42 37 84 331 المتوسط الحسابي لمجموعة البيانات هذه = (مجموع القيم ) / 40 = 23.10 وزارة التعليم Ministry of Education 2024-1446 الفصل 9 312

يمكن للقيم الطرفية التأثير لمحة سريعة أي من النتيجتين تمثل القيمة النموذجية لمجموعة البيانات أفضل تمثيل؟ في هذا المثال، يقدّم الوسيط توصيفًا أفضل للبيانات مقارنةً بالمتوسط الحسابي، وهذا مردّه لقيمة طرفية Outlier الأكبر بكثير من القيم الأخرى الموجودة ضمن مجموعة البيانات. قد يتأثر المتوسط الحسابي بمجرد وجود قيمة واحدة هي أعلى بكثير أو أقل بكثير من سائر القيم في مجموعة البيانات، تسحب القيمة الطرفية المتوسط باتجاهها. تعريف في النتيجة لذلك يجب التعامل معها بحذر. في بعض الحالات يمكن حذف القيمة الطرفية البيانات قبل البدء بالأعمال الطرفية Outlier : قيمة ضمن مجموعة البيانات هي أعلى بكثير أو أقل بكثير من سائر القيم في مجموعة البيانات. من مجموعة • يمثل المنوال Mode في مجموعة البيانات القيمة الأكثر تكرارًا في المجموعة. هو مقياس آخر من مقاييس النزعة المركزية، وقيمته الوصفية أقل مقارنة بالمتوسط الحسابي أو الوسيط. يمكن أن يكون المنوال مفيدًا بشكل خاص في بعض التحليلات التي تستفيد من اكتشاف وجود قيمة تتكرر أكثر من سواها. تعريف الحسابية. في بعض الحالات الأخرى، قد يكون من الأفضل استخدام الوسيط بدل من المتوسط الحسابي. المنوال Mode القيمة الأكثر تكرارًا في المجموعة. قد لا يكون المنوال رقمًا واحدًا. الشكل "9-1" : المتوسط الحسابي، والوسيط، والمنوال المتوسط الحسابي الوسيط المتوسط الحسابي هو المتوسط الوسيط هو القيمة المنوال ء المنوال يمثل القيمة الأكثر أو مجموع قيم مختلف عناصر الوسطى في مجموعة تكرارا في المجموعة. مجموعة البيانات مقسم على عدد البيانات بعد ترتيب القيم عناصر مجموعة البيانات. المتوسط الحسابي = مجموع قيمة مختلف عناصر العينة / عدد عناصر العينة ضمن تسلسل. مثلا ، إذا كان لدينا مجموعة القيم التالية = 2 ، 2، 3، 4، 5، إذن: المتوسط الحسابي = (2+2+3+4+5)/5 = 3.2 الوسيط = 3 المنوال = 2 مثال عدد الزيارات إلى موقع إلكتروني تعليمي التحق 40 طالبًا بمادة العلوم في مدرسة أهلية في جدة جهّز أستاذ المقرر المادة الدراسية، والدرجات، والملحوظات الصفية، ووضعها على الموقع الإلكتروني المخصص للمادة لتكون بمتناول أيدي الطلبة. تتبع الخادم (server) عدد زيارات كل طالب لصفحات هذا الموقع. وبعد استخدام البيانات لدعم عملية اتخاذ القرآن الـ 313 Ministry of Education 2024-1446

يمكن للقيم الطرفية التأثير في النتيجة
عدد الزيارات إلى موقع إلكتروني تعليمي
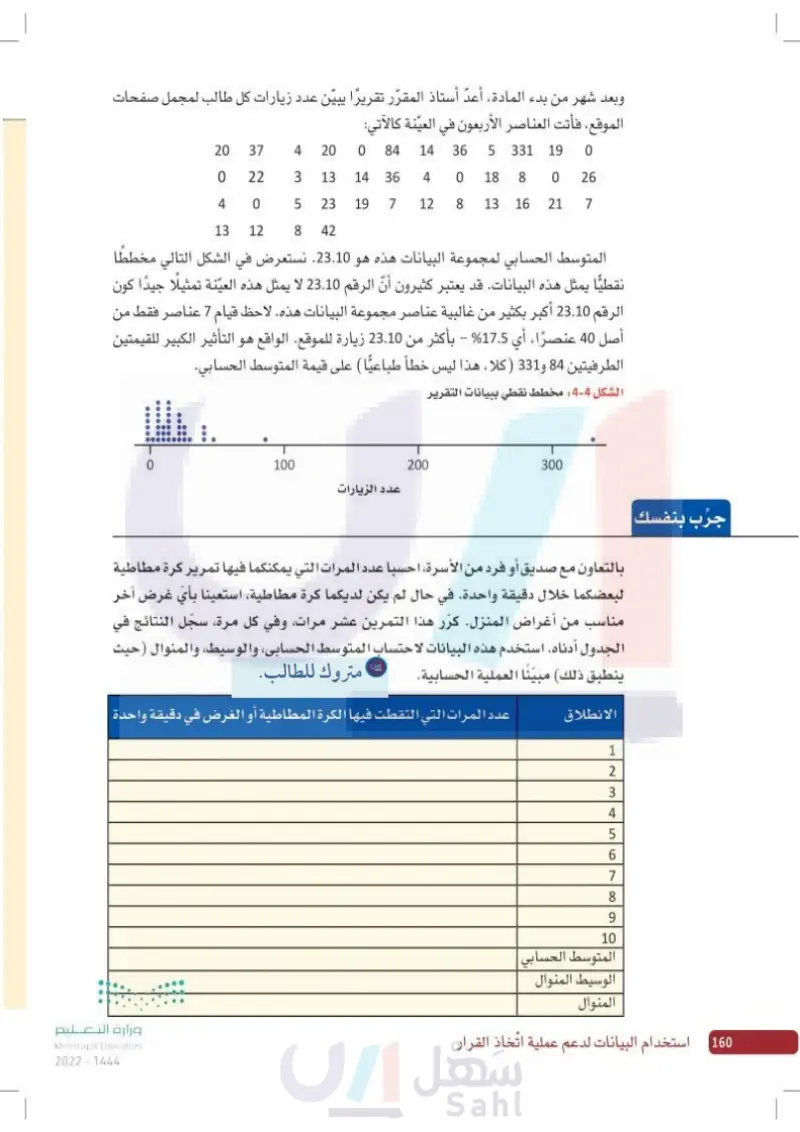
314 شهر من بدء المادة، أعد أستاذ المقرر تقريرًا يبين عدد زيارات كل طالب لمجمل صفحات الموقع ، فـ ، فأتت العناصر الأربعون في العينة كالآتي: 20 20 37 4 0 84 331 5 36 14 19 0 0 22 3 13 14 36 18 4 0 8 0 26 405 23 19 7 12 8 16 13 21 7 13 12 8 42 المتوسط الحسابي لمجموعة البيانات هذه هو 23.10 x . نستعرض في الشكل التالي مخططا نقطيًّا يمثل هذه البيانات. قد يعتبر كثيرون أن الرقم 23.10. لا يمثل هذه العينة تمثيلا جيدًا كون الرقم 23.10 أكبر بكثير من غالبية عناصر مجموعة البيانات هذه. لاحظ أن 7 عناصر فقط من أصل 40 عنصرًا ، أو 17.5 ، هي أكبر من 23.10 . الواقع هو التأثير الكبير للقيمتين الطرفيتين 84 و 331 (كلا ، هذا ليس خطأ طباعيًّا على قيمة المتوسط الحسابي . الشكل "و - 4" : مخطّط نقطي ببيانات التقرير جرب عدد الزيارات بنفسك 0 100 200 300 بالتعاون مع صديق أو فرد من الأسرة احسبا عدد المرات التي يمكنكما فيها تمرير كرة مطاطية لبعضكما خلال دقيقة واحدة. في حال لم يكن لديكما كرة مطاطية، استعينا بأي غرض آخر مناسب من أغراض المنزل. كرّر هذا التمرين عشر مرات، وفي كل مرة، سجل النتائج في الجدول التالي. استخدم هذه البيانات لاحتساب المتوسط الحسابي، والوسيط والمنوال (حيث ينطبق ذلك) مبيّنًا العملية الحسابية. الانطلاق 1 234567 8 9 10 المتوسط الحسابي الوسيط المنوال المنوال الفصل 9 عدد المرات التي التقطت فيها الكرة المطاطية أو الغرض في دقيقة واحدة وزارة التعليم Ministry of Education 2024-1446

مخطط نقطي ببيانات التقرير
أسئلة مراجعة 1. تجد في ما يلي أسعار ستة أنواع إطارات شاحنات فازت بأعلى نسبة تصويت من العملاء في العام 2018 (الأسعار هي بالريال السعودي 159.00 199.00 157.00 127.65 123.99 126.00 ب. احسب قيمة المتوسط الحسابي والوسيط. ما سبب الفارق بين هاتين القيمتين؟ ج أي من القيمتين - المتوسط الحسابي أو الوسيط - يصف بشكل أفضل القيمة النموذجية في مجموعة البيانات هذه؟ 2. حددت دراسة طبية أجريت مؤخرًا كمية الصوديوم الموجودة في الحصة الغذائية الواحدة من 11 نوعًا من زبدة الفستق (الكمية بالميليغرام 150 120 140 50 120 150 150 170 65 لک 250 اعرض هذه البيانات على مخطط نقطي، بيّن ملحوظاتك على الخصائص غير الاعتيادية في هذا المخطط. 110 .i ب. احسب المتوسط الحسابي والوسيط من محتوى الصوديوم في كلّ عيّنة زبدة فستق. ج. تتشابه قيمة المتوسط الحسابي وقيمة الوسيط في هذه المجموعة من البيانات. أي الجوانب الأخرى التي يبينها المخطّط النقطي (من السؤال (أ) عن توزّع قيمة محتوى الصوديوم تشرح سبب تشابه قيمة المتوسط الحسابي وقيمة الوسيط؟ استخدام البيانات لدعم عملية اتخاذ القرآن الـ 315 Ministry of Education 2024-1446