الرياضيات أحيائي الفصل الأول: الأعداد المركبة 1-6 التمثيل الهندسي للأعداد المركبة

التمثيل الهندسي للأعداد المركبة - الرياضيات أحيائي - سادس اعدادي

الفصل الأول: الأعداد المركبة

1-1 الحاجة إلى توسيع مجموعة الأعداد الحقيقية

1-2 العمليات على مجموعة الأعداد المركبة

1-3 مرافق العدد المركب

1-4 الجذور التربيعية للعدد المركب

1-5 حل المعادلة التربيعية في (c)

1-6 التمثيل الهندسي للأعداد المركبة

1-7 الصيغة القطبية للعدد المركب

1-8 مبرهنة ديموافر

الفصل الثاني: القطوع المخروطية

القطوع المخروطية وأهمية دراستها

2-1 القطع المخروطي

2-2 القطع المكافئ

2-3 القطع الناقص

2-4 القطع الزائد

الفصل الثالث: تطبيقات التفاضل

3-1 المشتقات ذات الرتب العليا

3-2 المعادلات المرتبطة

3-3 مبرهنتا رول والقيمة المتوسطة

3-4 اختيار التزايد والتناقص للدالة باستخدام المشتقة الأولى

3-5 النهاية العظمى والنهاية الصغرى

3-6 تقعر وتحدب المنحنيات ونقط الانقلاب

3-7 اختبار المشتقة الثانية لنقط النهايات العظمى والصغرى المحلية

3-8 رسم المخطط البياني للدالة

3-9 تطبيقات عملية على القيم العظمى أو الصغرى

الفصل الرابع: التكامل

4-1 النظرية الأساسية للتكامل - الدالة المقابلة

4-2 خواص التكامل المحدد

4-3 التكامل غير المحدد

4-4 اللوغارتم الطبيعي

4-5 إيجاد مساحة المنطقة المستوية

4-6 الحجوم الدورانية

الفصل الخامس: المعادلات التفاضلية الاعتيادية

5-1 مقدمة

5-2 حل المعادلة التفاضلية الاعتيادية

5-3 الحل الخاص والعام للمعادلة التفاضلية الاعتيادية

5-4 المعادلات التفاضلية الاعتيادية من المرتبة الأولى والدرجة الأولى

5-5 بعض طرق حل المعادلات التفاضلية

الفصل السادس: الهندسة الفضائية

6-1 تمهيد

6-2 الزاوية الزوجية والمستويات المتعامدة

6-3 الاسقاط العمودي على مستو

تمارين عامة

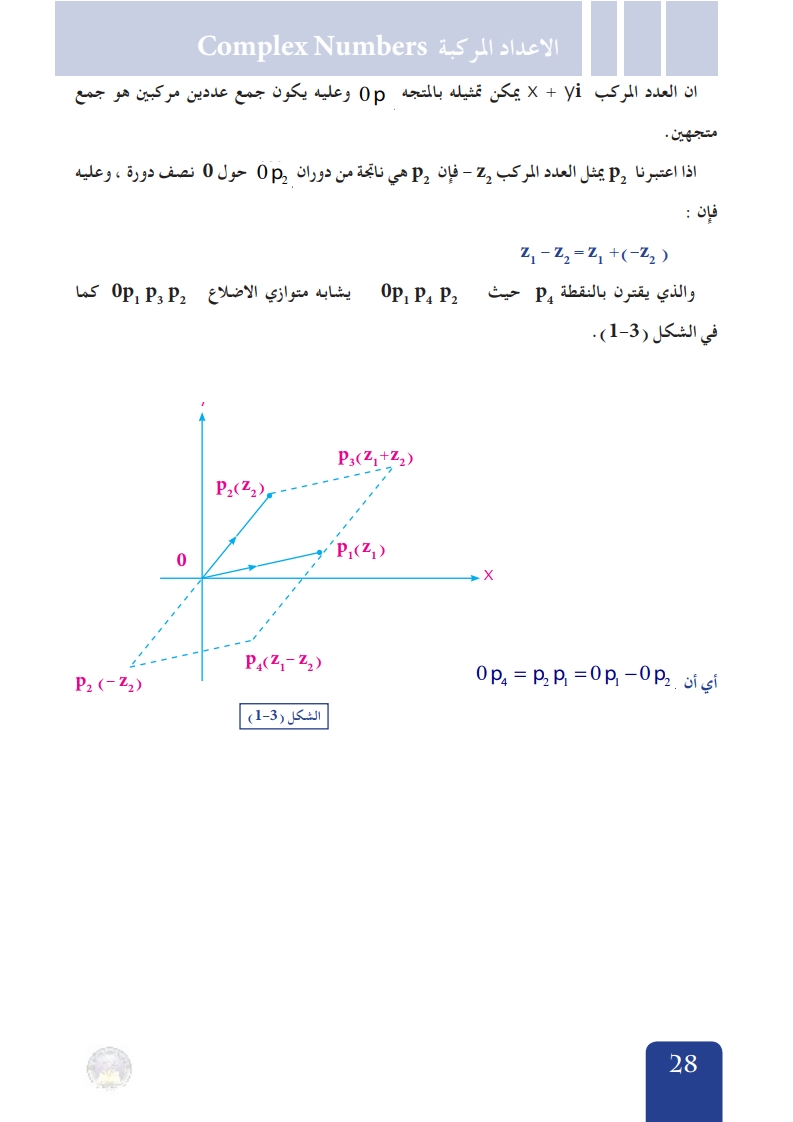
1-6 التمثيل الهندسي للأعداد المركبة

التمثيل الهندسي للأعداد المركبة

شرح التمثيل الهندسي للأعداد المركبة

1-6 التمثيل الهندسي للأعداد المركبة

ان العدد المركب x+yi يمكن تمثيله بالمتجة

1-6 التمثيل الهندسي للأعداد المركبة

مثال 19 مثل العمليات الاتية هندسيا في شكل ارجاند

شرح مثال 19 مثل العمليات الاتية هندسيا في شكل ارجاند

1-6 التمثيل الهندسي للأعداد المركبة

اكتب النظير الجمعي لكل من الاعداد الآتية ثم مثل هذه الاعداد ونظائرها الجمعية على شكل ارجاند

شرح اكتب النظير الجمعي لكل من الاعداد الآتية ثم مثل هذه الاعداد ونظائرها الجمعية على شكل ارجاند

اكتب العدد المرافق لكل من الاعداد الآتية ثم مثل هذه الاعداد ومرافقاتها على شكل ارجاند

شرح اكتب العدد المرافق لكل من الاعداد الآتية ثم مثل هذه الاعداد ومرافقاتها على شكل ارجاند

اذا كان z=4+2i فوضح على شكل ارجاند كلا من

شرح اذا كان z=4+2i فوضح على شكل ارجاند كلا من

اذا كان z2=1+2i , z=4+2i فوضح على شكل ارجاند كلا من

شرح اذا كان z2=1+2i , z=4+2i فوضح على شكل ارجاند كلا من