قانون الجاذبية وقوانين كبلر - علوم الأرض والفضاء - ثالث ثانوي
القسم الأول 1-1
الفصل1: تطور الكون
الفصل2: الميكانيكا السماوية
الفصل3: المعادن
الفصل4: الصخور
الفصل5: الصفائح الأرضية وآثارها
الفصل6: البراكين والزلازل
القسم الثاني 1-2
الفصل1: المجموعة الشمسية
الفصل2: البيئة الفضائية
الفصل3: الأجهزة الفلكية
الفصل4: الأحافير والتأريخ الصخري
الفصل5: الطاقة ومصادرها
الفصل6: جيولوجيا المملكة العربية السعودية
21 الفصل الميكانيكا السماوية الفكرة العامة تخضع الأجرام السماوية والأنظمة الفضائية المجموعة من التوالين التي تحدد خصائص حركتها وديناميكيتها السماوية. 21 قانون الجاذبية وقوانين كبلر ال الرئيسة قوانين كبلر نصف شکل وخصائص حركة الأجرام التي تسلكها حول بعضها، والسرعات التي تتحرك بها، والكتل المتبادلة بينها. 22 التقلية الفضائية المات الرئيسة استطاع الإنسان بواسطة التقنيات الفضائية الوصول إلى أجرام لم تكن المناظير الفلكية كافية للدراستها. حقائق فلكية . حينما تتطلق المركبات الفضائية نحو الفضاء فإنها تبدأ رحلتها من الأرض بمسار المنحن وليس مستقيما - كما في الصورة. 40 Celestial Mechanics درازة البا

نشاطات تمهيدية تجربة استهلالية هل تتحرك جميع الاجسام في نظام الشمسي بالسرعة نفسها ؟ تحرك أجرام السماء حول بعضها في مدارات اهليليجية، وتتأثر حركتها بالعديد من العوامل: كالمسافات والقوى المتبادلة فيما بينها. الخطوات BBC 1. أحضر حوضين دائريين قطر الأول 1m وقطر الآخر 0.5m، وقم بوضع علامة نقطية على طرف محيط قاع كل منهما. 2 ادفع كرة حديدية صغيرة بشكل دائري حول محيط قاع الحوض الكبير، وقم بحساب الزمن الدوري. 3 أعد الخطوة 2 للحوض الصغير. التحليل 1. قارن بين زمني دوران الكرة في الحوضين. ماذا تلاحظ 2. ما علاقة قطر الحوضين بالزمن الدوري؟ 3 هل تتوافق نتائج تجربتك مع زمن دوران الكواكب حول الشمس. فسر ذلك ؟ المطويات منظمات الأفكار اصنع المطوية الآتية لتتعرف على أنواع المركبات الفضائية الخطوة 1: ضع ورقتين من دفترك إحداهما فوق الأخرى، بحيث تبعد إحداهما عن الأخرى cm 2 تقريبا، كما في الشكل المجاور. الخطوة 2: إلى الطرف السفلي للورقتين التكوين حبة السنة متساوية. لم أضغط بقوة على الجزء المطري لتشتت الألسنة في أماكنها . الخطوة 3: ثبت أوراق المطوية معا بالدبابيس، وعون الألسنة بأنواع المركبات الفضائية: الأقمار الصناعية المحطات الفضائية، المركبات المأهولة، و المركبات غير المأهولة اميم حده التامة في أثناء دراستك القسم 2-2، لتتعرف على مميزات كل نوع، واعط مثالا على كل نوع مبينا أهميته alja 41

اصنع المطوية الآتية لتتعرف على أنواع المركبات الفضائية
2-1 الأحداف يحسب زمن دوران حرم حول الشمس. يحسب وزن جسم ماعلى کوکب قانون الجاذبية وقوانين كبلر قلم الكاري The law of gravity and kepler's laws است الاسس قوانين كبلر تصف شكل وخصائص حركة الأجرام التي تسلكها حول يحسب سرعة حروب قمر بعضها والسرعات التي تتحرك بها، والكتل المتبادلة بينها. صناعي. الربط مع الحياة حينما تتابع بنا مباشرًا النهائيات كأس العالم في كرة القدم، فإن هذا الأمر لم يكن ممكناً إلا من خلال وضع أقمار صناعية في المدار الصحيح بدقة حول الأرض، وذلك استنادا إلى مجموعة قوانين فيزيائية ميكانيكية، توصل إليها الإنسان من خلال رصد الأجرام السماوية، ووضع حسابات تتوافق مع الرصد وذلك من أجل فهم وتفسير الظواهر المسيار مركبة فضائية تستعمل الملكية كالخوف والكسوف الشكل 2 و شروق وغروب الشمس. وعمل تقاويم لاستكشاف الفضاء الخارجي؛ الأشهر السنة ولتحديد مواقيت العبادة من حج وصوم وتحديد مواسم الزراعة، وعمل مراجعة المفردات حيث يتم إطلاقها في الفضاء محاكاة حاسوبية لتحديد المواقع واتجاه الحركة الشكل 2-2. ومن أبرز هذه القوانين قوانين الخارجي بهدف استكشاف واحد كبار التي تستخدم لحساب خصائص مدارات الأقمار الصناعية وليس فقط في معرفة المدارات في النظام الشمسي، وهذه القوانين اكتشفها الفلكي (يوهانس كبلر Johannes kepler) خلال القرن السابع عشر الميلادي بعد توافقها مع أرصاد "تيخو براهي" لكوكب أو أكثر من الأجرام السماوية. المفردات الجديدة قانون كيلر الأول البعد الحضيضي البعد الأوجي قانون كيلر الثاني قانون كبلر الثالث المريخ سرعة الهروب 42 الشكل 1-2 كسوف شمسي كلي. الشكل 22 تحديد المواقع بواسطة نظام الملاحة العالمي. درارة التعليم

قوانين كبلر تصف شكل وخصائص حركة الأجرام التي تسلكها حول بعضها والسرعات التي تتحرك بها والكتل المتبادلة بينها

الشكل 1 تحديد كسوف شمسي كلي
قوانين كبلر قانون كبلر الأول Kepler Laws Kepler's First Law ينص قانون كبلر الأول Kepler's First Law على أن الكواكب تدور حول الربط مع الرياضيات القطع الناقص هو المحل الشمس في مدارات على شكل قطع ناقص، وتقع الشمس في إحدى بؤرتيه كما في الهندسي لمجموعة النقاط في المستوى الشكل 24 خصائص القطع الناقص يوضح الشكل 3 بعض خصائص القطع الناقص ؛ فمثلا المسافة A,A=2a هي المحور الأكبر والمسافة BB26 هي المحور الأصغر ونصف المحور الأكبر للقطع الناقص ترمز له بالرمز a ونصف المحور الأصغر للقطع الناقص ترمز له بالرمز 6 ومركز القطع الناقص هو . والقطع الناقص له بؤرتين E و F. وأيضا كلما صغرت المسافة FE. اقترب شكل القطع من شكل الدائرة، بينما كلما زادت المسافة FR زادت بيضاوية القطع أو تفلطح القطع . ويستعمل الرمز التعريف تفلطح القطع، ويسمى "الاختلاف المركزي". للاطلاع الذي يكون مجموع بعديها عن نقطتين ثابتين يساوي مقدارا ثابتا تمى هاتان النقطتان بالبؤرتين. الراس الرامي المرافق الموكو المواس المرافق ... المحور الأكبر المراسي البورتات 43 مراره e= CF = ae FF e-ga B Q b A A F C a B. الشكل 3-2 خصائص القطع الناقص

القطع الناقص هو المحل الهندسي لمجموعة النقاط في المستوى
خصائص القطع الناقص
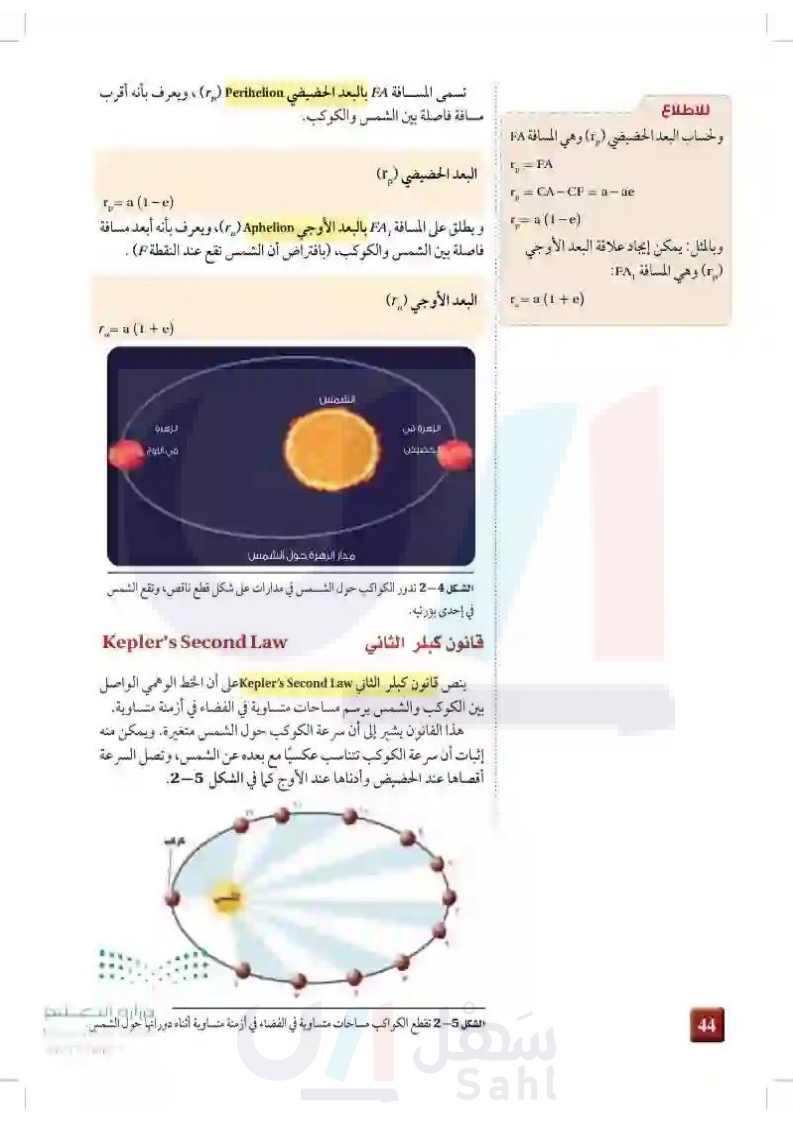
للاطلاع ولحساب البعد الحضيضي (1) وهي المسافة FA تسمى المسافة PA بالبعد الحضيضي r) Perilion) ، ويعرف بأنه أقرب مسافة فاصلة بين الشمس والكوكب. = PA r = CA-CP = 0 البعد الحضيضي (٢) -a (1-e) =a (1-e) و يطلق على المسافة FA بالبعد الأوجي r) phelion)، ويعرف بأنه أبعد مسافة وبالمثل: يمكن إيجاد علاقة البعد الأوجي فاصلة بين الشمس والكوكب، بافتراض أن الشمس تقع عند النقطة ) . (1) وهي المسافة PA 44 =(1+e) البعد الأوجي (٢) 7=(1+0) الشمس الزهرة بين الزهري في اليوم فجار الزهرة حول الشمس الشكل 24 تدور الكواكب حول الشمس في مدارات على شكل قطع ناقص، وتقع الشمس في إحدى بورتيه. قانون كبلر الثاني Kepler's Second Law ينص قانون كبلر الثاني Kepler's Second Law على أن الخط الوهمي الواصل بين الكوكب والشمس برسم مساحات متساوية في الفضاء في أزمنة متساوية. هذا القانون يشير إلى أن سرعة الكوكب حول الشمس متغيرة، ويمكن منه إثبات أن سرعة الكوكب تتناسب عكسيًا مع بعده عن الشمس، وتصل السرعة أقصاها عند الحضيض وأدناها عند الأوج كما في الشكل 25 عرف حرارة التعليم الشمسية الشكل 25 تقطع الكواكب مساحات متساوية في الفضاء في أزمنة متساوية أثناء دورانها -

يمكن إيجاد علاقة البعد الأوجي وهي المسافة FA
قانون كبلر الثالث Kepler's Third Law ينص قانون كبلر الثالث Kepler's Third Lay على أن مربع مدة دورة الكوكب مشروع كبار الفضائي حول الشمس تتناسب مع مكعب نصف طول المحور الأكبر لمداره الشكل 6-2 إذا كان: T= زمن دورة الكوكب حول الشمس، a = نصف المحور الأكبر لمدار الكوكب فإن Taa إذا قسنا T بالسنة النجمية (years) ، وقسنا a بالوحدة الفلكية (AU) تقديرا لجهود العالم كبلر في محال علم الفلك (الوحد الفلكية هي: متوسط المسافة بين الأرض والشمس، وتساوي 150 مليون فقد اطلقت وكالة ناسا مشروعا قضائيا باسمه، کیلومتر) فإن الثابت = 1 الصيغة الرياضية قانون كبار الثالث T²=a³ وهو عبارة عن مرصد فضائي تم إطلاقه إلى الفضاء من اجل استكشاف ما إذا كانت هناك حياة في كواكب نجوم مجرة درب التبانة، حيث قام باكتشاف أكثر من 2600 تركب نجمي إلى الآن. وجمع المرصد كمية هائلة من البيانات التي سيستمر تحليلها لسنوات. مثال 1 مذنب يدور حول الشمس في مدار قطع ناقص تفلطحه 0.97، وصل إلى أقرب نقطة للشمس على بعد 04540. احسب مدة دورة هذا المذنب حول الشمس بالسنوات. تحليل المسالة ورسمها الرسم وضح المعقب حول الشمسي المجهول المعلوم 045AU ,=0.45AU e=0.97 T=? ابجاد الكمية المجهولة حل قانون البعد الحضيضي لإيجاد نصف قطر المحور الأكبر التعويض حساب مدة دوران المذئب حول الشمس بالسنوات حل قانون كبلر الثالث التمريض - تقويم الجواب هل الوحل اب ساحة ستكون وحدة مدال دوران حرم حول الشمسى بالسلة. a I-e a= 0.45 1-0.97 = 15 AU T=a√a T = 15√√15 T= 58.1 Year خريج من ان الکرک مول الی ۱ الشكل - علاقة من دورة الكواكب المدارية حول الشمس يبعده عنها حسب قانون كبار الثالث. قراره ای 45

مذنب يدور حول الشمس في مدار قطع ناقص تفلطحه 0.97، وصل إلى أقرب نقطة للشمس عل بعد 0.45 احسب مدة دورة هذا المذنب حول الشمس بالسنوات
قانون كبار الثالث المعدل : Modified 3 Kepler's law في عام 1687 قام نيوتن بتعديل قانون كبلر الثالث وفقا لقوانينه الخاصة للحركة وقانون الجذب العام. للاطلاع قانون كبلر الثالث المعدل قانون كبار الثالث المعدل a=TM من قانون الجذب العام لنيوتن يمكن إثبات أن : ملاحظة عند حل المسائل: Tea GM-m حيث كتلة الشمس، m كتلة الجزم. إذا أخذنا السنة وحدة القياس الزمن والوحدة الفلكية A10 القياس المسافة التحويل الكتلة إلى كتلة شمسية يكون بقسمة الكتلة على كتلة الشمس التحويل البعد إلى وحدة فلكية: يكون بقسمة المسافة على مسافة الأرض عن الشمس. مثال 2 مركبة فضائية تدور حول الأرض في مدار بيضاوي على متوسط بعد يساوي 10 أضعاف نصف وكتلة الشمس لقياس الكتلة، فإن قطر الأرض ، احسب مدة دورتها حول الأرض .day. علماً بأن نصف قطر الأرض 6378=R الثابت يساوي واحد (1) أي أن G a=T(M.m) إذا طبقنا هذا القانون الجرم يدور حول الشمس فإن kam وكتلة الأرض Me=6x10kg وكتلة الشمس Ms=2x10kg. الحل المعلوم a=10R, km 6ة المجهول T=? 30 46 M.=6x10 kg a=TM ايجاد الكمية المجهولة . بقسمة بعد المركبة على 1510 (متوسط يعد الأرض عن التلفي | الحساب بعد المركبة بالوحدة الفلكية .AU 4.25x10 AU بقسمة كتلة الأرضى على كتلة الشمس لحساب كتلة الأرض بدلالة كتلة الشمس 63780 15x10 ادة M= M. = M 6x1026 2x100 = 3x10 M من قانون كتير الثالث المعدل / تهمل كتلة المركبة لسفرها مقابل كتلة الأرضى ) بالضرب 25 365 التحويل إلى duyes . تقويم الجواب a = PM T= a (4.25x10) M T= 2.55x10- 3×10-0 7.67x10-" 3x10 T=√2.55x10 T= 5.1x10-years T=5: 1x10 x 365.25=1.84 day هل الوحدات صحيحة استكون وحدة مدة دورات المركبة حول الأرمني . درارة التصليح

ایجاد كتلة كوكب له تابع من الممكن ايجاد كتلة كوكب له تابع إذا علم نصف المحور الأكبر ومدة الدوران للكوكب وتابعه كالأتي للاطلاع GM-m كتلة الشمس M كتلة الكوكب m مثال 3 m- M يبعد القمر كارون عن مركز بلوتو km 19700، فإذا كانت مدة دورانه حول بلوتو هي 6.4 day أوجد كتلة بلوتو. علما بأن الفترة المدارية لبلوتو هي year 248 وبعده عن الشمس ALU .40 الحل تحليل المسألة ورسمها للكوكب () () = (a) اللتابع (a) = (r) (mm) إذا أهملنا كتلة التابع مقارنة بكتلة الكوكب في البسط أي أنه = ,m وكتلة الكوكب مقارنة بكتلة الشمس في المقام 0 = m التالي سكون كتلة الكركب m+m M+m m M (+)-(2) a = المعلوم المجهول =? T₁=248 year T=6.4 day a=40 AU a, 19700 km M=2x10kg برتو m إيجاد الكمية المجهولة. بقسمة الفترة المدارية الكترول على 863.25 لتكون بوحدة (year) 1.75x10-year بقسمة بعد كارون في بلوتو على 15x10 لتكون بوحدة ( الوحدة الفلكية (A) حل قانون إيجاد كتلة كوكب من كتلة جرم تابع له 6.4 365.25 19700 = 1.3x10-AU 158107 بالتعويض لإيجاد كتلة بلوتو - تقويم الجواب: 248 1.75x10-2 حل الوحدات سجحة ؟ سكون وحدة كتلة بارتون (( T= m= M (1.3×10 m= 2x100 1.3x10 40 m= 2x10x3.4x10 17×2×10 m= 1.3x1018 Loja

قانون الجذب العام لنيوتن Newton's Gravitational Law كان إسحاق نيوتن Isaac newton أول من وضع صيغة رياضية لقوة الجاذبية بين جسمين عام 1687م في كتابه principia. ينص القانون على أن قوة الجاذبية F بين جسمين تتناسب طرديا مع كتلتيهما وعكسياً مع مربع المسافة بينهما. Mm F=G: الاطلاع: فإذا كانت لدينا كتلتان، ولتكن الشمس والأرض مثلا كنها في الشكل 27 فإن هناك قوة جذب من كتلة الشمس على كتلة الأرض تعطى بالعلاقة F=G- Mm يمثل ثابت الجذب الكوني عجلة الجاذبية للكوكب تساوي: (1) Adm Fx Mg = G May إذا افترضنا أن هذا الكوكب هو الأرض فإن تسارع الجاذبية الأرضية . 9,-G9 g 9. و 9. Gry (2) يعطي بالعلاقة حيث كتلة الأرض بأخذ النسبة بين 9 و 2 هي كتلة الكوكب بدلالة كتلة كوكب الأرض وتساوي هي نص قطر الكوكب بدلالة نصف قطر كوكب الأرض وتساوي 99. إذا افترضنا أن الشكل 22 قوة جذب كتلة الشمس على كتلة الأرض. هان وبما أن وزن جسم كتلته على سطح كوكب يساوي قوة جذب الكوكب W = m.g W=m, g W کرارة التعليم (1) (2) لهذا الجسم تساوي: وزنه على الأرض: إذا وزن هذا الجسم على الكوكب بدلالة وزنه على الأرض: W m.9. 48

لوزن الجسم على الكوكب بدلالة وزنه على الأرض يعطى بالعلاقة : مثال 4 W=W, 9 كوكب كتلته تساوي 0.01 من كتلة الشمس وتصف قطره يساوي تصف قطر الأرض. 1. احسب جاذبيته مقارنة بجاذبية الأرض. 2. افترض أن رائد فضاء وزنه على الأرض يساوي 100N هبط على هذا الكوكب فكم يبلغ وزنه بعد هبوطه عليه ؟ الحل تخليل المسألة ورسمها. العلوم المجهول W=100N m,=1.01M, = 2x108 إيجاد الكمية المجهولة. بحساب كتلة الكوكب بالنسبة الكتلة الأرض W =? mp m me 2x10 6x10 = 3333m حل قانون وزن جسم على كوكب بدلالة وزنه على الأرض بالتعويض تكون جاذبية الكوكب بحساب وزن والد القضاء على الكوكب - تقويم الجواب: g=3333 g, MB-M g 9 W=3333 W W = 3333x100 = 33,3x10 على الوحدات جعة الوحدة وقدراته القضاء بالنيوتن هل الحراب منطقي ؟ نعم لأن والله على هذا المكا اتف وايه على الأرض بمطار الا مرة دراره 49

الربط مع الجار العلماء الاسلام السرعة المدارية لجرم سماوي Orbital Velocity For a Celestial Body وهي تمثل سرعة جرم حول جرم آخر ومن قانون الجذب العام وعلى سبيل المثال حركة جرم كتلته m حول جرم كتلته ، فإن سرعة الجرم ٧ في حالة كون المدار قطع ناقص - تحقق المعادلة للاطلاع V=G(M.m) استحق أن يكون "ابن الشاطر" هو علهم علماء الفلك لاستنتاج نظرية مركزية السمن النظامنا الشمسي بدلا في حالة دوران جرم حول الشمس أو مركبة فضاء حول القمر، فإن كتلة الجرم الدوار تهمل لصغرها بالنسبة للكتلة الأخرى، فتصبح المعادلة كالآتي: للاطلاع V2= ( من الأرض، إنه من المعروف منذ فترة ويمكن كتابتها على الصيغة التالية إذا قسنا و a بالوحدة الفلكية والكتلة M طويلة أن نماذج "كوبرنيكوس " المركزية بدلالة كتلة الشمس، فإن السرعة ، ستكون بوحدات km sec الشمس نماذج ابن الشا قد استخدم واضحا مع كوبرنيكوس الحركات غير المنتظمة لمؤشرات الكواكب التي أحدثها بطليموس ويتضح هنا أن للاطلاع V - 301 2 نماذج ابن الشاطر لها في الواقع الحيازا في حالة حركة جرم حول الشمس فإن M ستمثل كتلة الشمس وهي تساوي المركزية الشمن مما جعلها مناسبة واحد وتصبح المعادلة بشكل خاص كأساس النماذج مركزية الشمس. 50 V=30 a مثال 5 في المثال 1 السابق كم تبلغ أدنى سرعة للمذنب ؟ حيث قيمة الاختلاف المركزي 0.97 ونصف قطر المحور الأكبر 15AU المحل تحليل المسألة ورسمها ارسم حركة المذنب حول الشمس وحدد أوجه المعلوم e=0.97 a=15 AU ايجاد الكمية المجهولة حل قانون البعد الأوجي T المجهول -30 AU- V=? t=a(1+e) درارة التعليم 5=15(1+0.97)-29.55 AU

حل قانون السرعة المدارية لجرم سماوي بالتعويض لايجاد اللي سرعة للمذهب - تقويم الجواب : =0.94 Km/s V=30 a V = 30 2 29.55 15 هل الوحدات صحيحة أو علة السرعة الطبارية للبنك / em على الجواب منطقي العم يحكم أن هذه الشركة القلب وهو في الخطة الأود سرعة الهروب Escape Velocity سرعة الحروب Escape Velocity: في السرعة اللازمة لجسم ما للدخول في مسار على شكل قطع مكافئ حول كوكب ما ثم الهروب من جاذبيته الشكل 8-2 مثال 6 V= 2GM R km/sec فكر معنا کیف تهرب المركبات الفضائية خارج كوكب الأرضي ؟ رعة الإفلات السرعة المدارية أوجد سرعة الهروب لكوكب كتلته 7.5x10 kg ونصف قطره m 10×1.5 الشكل 28 سرعة الإفلات لقمر صناعي . علما بأن ثابت الجذب العام N.m/kg 10×6.67. الحل تحليل المسالة ورسمها . المعلوم M=7.5x102 KB R=1.5x10 km إيجاد الكمية المجهولة حل قانون سرعة الهروب بالتعويض لايجاد سرعة الهروب للكوك - تقويم الجواب المجهول V_=? V R 2X6.67x10"x7.5x10 1.5x10 V=2.5 km/s هل الوحدات محيحة أو علة سرعة الهروب الكركي لرحلة . 51 Loja

نشاط عملي تمثل رحلة مشروع أرتيمس للقمر الشكل -- مثال حي على انتقال جرم تمثيل سرعة الهروب من جاذبية الأرض بين أنظمة مدارية الجرمين سماويين هما: الأرض والقمر، وذلك حينما تبلغ مغناطيس كرات حديد - غطاء بلاستيكي كبير. سرعة إفلاته من الأرض km s 11 لينطلق ناحية القمر في مسار قطع مكافئ ليدخل مداره و يسير بسرعة مدارية تختلف بحسب ارتفاعه عن القمر، وبعد إكمال مهمته ينطلق من مداره حول القمر بسرعة إفلات km s 2.4 عائدا نحو ورق مقوى شريط لاصق الخطوات . قص الورق المقوى بطول 30 سم وعرض 10 سم، واثن الورقة على شكل مجرى ماني ذو طرفين. . ضع المغناطيس في طرف الغطاء البلاستيكي الصق نهاية الورق المقوى بالمغناطيس . ضع كرة الحديد في بداية الورق المقوى واتركها تتدحرج إلى الأسفل. ارفع بداية الورق المقوى إلى الأعلى، ثم ضع كرة أخرى واستمر في الرفع مع دحرجة الكرات إلى أن تصل إلى درجة يصعب فيها على المغناطيس جذب كرات الحديد. التحليل ماذا تلاحظ ؟ قارن بين حركة الكراث المتحررة من المغناطيس وحركة جم يهرب من جاذبية الأرض. الأرض. التخلص من المرحلة الأساسية فصل السراج الاطلاق هبوط مركية فضائية بالمظلة الدخول في مدار انتقالي قمري الربط مع الفيزياء انطلاق الصواريخ الفضائية هو أحد تطبيقات قانون نيوتن الثالث الذي بنصر على أن لكل قوة فعل قوة رد فعل مسار له في المقدار ومعاكس له في الاتجاه، ومن امثلته احتراق الوقود في الصاروخ مولدا الغازات، حيث يعمل الصاروخ على دفع هذه الغازات للتخلص منها من خلال فتحة اسفل الصاروخ. أما قوة رد الفعل التي تولدها هذه الغازات فتدفع الصاروخ لأعلى. رحلة العودة 52 مدار قمري الشكل 29 رحلة مشروع أرتيم للقمر. حرارة التعليم

53 مختبر تحليل البيانات التفكير الناقد 1. ثمة حوالي 10 آلاف كويكب صغير يدور حول الشمس وبعضا منها يجوم قريبا من الأرض، وقد تكون خطيرة على البشر وكل ما هو على سطح الأرض الجدول التالي يستعرض بعضًا من هذه الكويكبات القريبة منا : سرعة المترايه بطله عمر الأرض النسبية 11 قطرد lm اسم الكويت 2022 YS0 1.786.449 0.01194 9.72 20.27 2022 YT6 B13.642 0.00544 201 L) 1,819,585 3.48 0.01216 1.816.884 9.92 0.01215 التحليل .2 كيف ألهمت قوانين كبير العلماء للوصول بنجاح إلى تصميم نظام إنذار مبكر للحد من أخطار الكويكبات ؟ 3. بناء على بيانات الجدول أي الكويكبات الواردة تتوقع انه يشكل خطرا على الأرض في حالة اذا اقترب منها . و لماذا ؟ 4. ابحث في الشبكة العنكبوتية عن كويكب اقترب مؤخراً من الأرض وقارن خصائصه بخصائص الكويكبات الواردة بالجدول . ماذا تلاحظ ؟ دراره

54 التقويم 1-2 الخلاصة ينص قانون كبار الأول على أن الكواكب الدور حول الشمس في مدارات على شكل فهم الأفكار الرئيسة احسب متوسط المسافة بين فيستا (كويكب) و بين الشمس علماً بأنه يستغرق year 3.63 للدوران حول الشمس قطع ناقص، وتقع الشمس في إحدى بؤرتيه . 2 وضح نوع العلاقة بين متوسط المسافة لفيستا ومدة دورانه حول ينص قانون كيلو الثاني على أن الخط الوهمي : الشمس الواصل بين الكوكب والشمس يرسم التفكير الناقد مساحات متساوية في العضاء في أزمة. متساوية. ينص قانون كبار الثالث على أن مربع مدة 3. لماذا يلجأ العلماء إلى قوانين كمل عند تعاملهم مع حركة المذنبات التي تتعدد مصادرها. دورة الكوكب حول الشمس تتناسب مع الرياضيات 20 الفلك مکعب نصف طول المحور الأكبر المدارد. .. أكملت وكالة الفضاء السعودية مهمتها على سطح القمر ولذا فهي ترغب بمغادرة مركبتها حدد سرعة هروبها من القمر إذا كانت كتلة القمر 7.3510kg ونصف القطر 10m × 1.5 دارة التعليم




 0
0 

 0
0