خطة حل المسألة الاستدلال المنطقي - الرياضيات 1 - رابع ابتدائي
الفصل الأول: القيمة المنزلية
الفصل الثاني: الجمع والطرح
الفصل الثالث: تنظيم البيانات وعرضها وتفسيرها
الفصل الرابع: الأنماط والجبر
نشاط الفصل الأول: القيمة المنزلية
نشاط الفصل الثاني: الجمع والطرح
نشاط الفصل الثالث: تنظيم البيانات وعرضها وتفسيرها
٤ - ٣ خُطَّأَ حَلَّ الْمَسْأَلَة رابط الدرس الرقمي فكرةُ الدَّرس: أستعمل خطَّةَ الاستدلال المنطقي لأحل المسألة. سلة يضعُ خمسةٌ منْ طُلاب الفصل قصاصات الورق في المُهمَلاتِ، وقدْ اصْطَفُّوا بعضُهُمْ خلفَ بعض مبتدئين بالأطول. فإذا كان عبد الله أطول من بدر وأقصر من فهد. وكانَ محمدٌ أقصرَ مِن شعودٍ، وأطول من فهد. فمَا التَّرْتِيبُ الَّذِي اصطفُوا بِهِ؟ افهم ما معطيات المسألة؟ kh حُلْ تَحَقَّق • عبدالله أطولُ مِن بدرِ. ، عبدالله أقصر من فهد. محمد أقصرُ مِن سُعود. • مُحمدٌ أطولُ مِن فهد. • اصطفّ الأصدقاء بعضُهم خلف بعض مبتدئين بالأطول. ما المطلوب؟ • تحديد الترتيب الَّذِي اصطفّ به الأصدقاء الخمسة. ابدأ باستعمال المعلوماتِ المنطقية المعطاة لتتوصل إلى الترتيب المطلوب. www.ien.edu.sa استعمِلْ مُعطياتِ المسألةِ لتُرَتِّبَ الأصدقاءَ، حيثُ تبدأُ باستعمال المعلوماتِ المَنطِقِيَّةِ. عبد اللهِ أطولُ مِن بدرٍ عبد الله أقصر من فهد محمد أطول من فهد محمد أقصر من سُعود الأطول ع 3 ع ف C إِذَنِ التَّرتيب هوَ: سُعود، محمد، فهد، عبدالله، بدر. راجع الحلَّ، سَتَجِدُهُ يَتَّفِقُ منطِقِيًّا مع معطياتِ المسألة. ع الأقصر ١١٤ الفصل الرابع: الأنماط والجبر وزارة التعليم Ministry of Education 2024-1446

خلل الخطة ارجع إلى المسألة السابقة، ثُمَّ أَجِبْ عن الأسئلة ١ - ٤: سو 1 هل ستتغيّر النتيجة لو نقصتْ إحدَى مُعطياتِ المسألة؟ إشرح إجابتك. ° ٣ إذا كانَ فهد أطول منْ سُعُودٍ وأقصر منْ عبدِاللَّهِ، وكانَ بدر أطولَهُمْ، واصطف محمدٌ ٤ خلفَ سعودٍ، فما الترتيب الذي اصطفوا به؟ وَضّحٌ لماذا كانتْ هذهِ الخُطَّةُ مناسبة لحل هذه هلْ يُمكنُ أنْ تَستعمِلَ خُطَّةً أُخرَى لحلَّ هذهِ المسألة. المسألة؟ إشْرَحْ إجابتك. تدرب عَلَى الخُطة استعمِلْ خُطَّةَ الاستدلال المنطقي لحل المسائلِ التَّالِيَةِ: 7 مع شعادَ الآنَ ٨ ريالات. أعطاها والدها أمس ٥:٤ الهَنْدَسةُ : يُوَضْحُ الشَّكلُ أدْنَاهُ أحدَ أَوْجُهِ ريالات، وأعطت أخاها ريالين. فكم ريالًا كان مُكَعب. إذا كانت الأوجه السِّتَّةُ متشابهةً، فما عددُ المُربَّعَاتِ الزَّرقاءِ فِي جَمِيعِ الأُوجُهِ؟ معها في البداية؟ القِيَاسُ : يبلغ طولُ مِضمارِ الجَرْيِ ٤٠٠ متر. ركض أسامة مسافة ٨٠ مترًا فِي المَرَّةِ الأُولى، ثُمَّ ركض ٦٠ مترًا في المرَّةِ الثَّانيةِ. فإذا كانَ قدْ بدأ من مسافةِ ٦ أمتار بعد خط البداية، فكم مترًا يَهْوَى كُلِّ مِن علي وعمر لعب كرة القدم، بقي ليصل إلى خط النهاية؟ وكُرةِ تنس الطَّاوِلةِ، والسباحة، فكم ترتيبا لتِلْكَ الألعاب يمكنهما القيام به؟ لدى محل لبيع أسماك الزينة ١٠ سمكاتٍ موزعةً على ٣ أحواض إذا باع منها ٤ سمكات، رِبَ ٥ أشخاص الحافلة في المحطَّةِ الأُولى. وبقي في كل حوض عدد مختلف من السمكِ، المحطَّةِ الثَّانية ركِبَ ٤ أشخاص ونزل فكم سمكةً بقيت في كل حوض؟ وفي شخصان. وفي المحطَّةِ الثَّالثةِ رَكِبَ ٥ أشخاص. وفي المحطة قبل الأخيرةِ رَكِبَ شخص واحدٌ ونزل ٤ أشخاص، فكم شخصًا أصبح في الحافلة؟ أكتب - كيف يمكنك حل المسألةِ رَقْمِ ۱۰ باستعمال خُطة الاستدلال المنطقي؟ وزارة التعليم ٤-٣- ARIS الدرس ٤ ٣- خطة حل المسألة Ministry bridation 2024-1446

يبلغ طول مضمار الجري ٤٠٠ متر ركض أسامة مسافة 80 متر في المرة الأولى ثم ركض 60 مترا في المرة الثانية فإذا كان قد بدا من مسافة 6 أمتار بعد خط البداية فكم متراُ بقي ليصل إلى خط النهاية؟


ركب 5 أشخاص الحافلة في المحطة الأولى وفي المحطة الثانية ركب ٤ أشخاص ونزل شخصان وفي المحطة الثالثة ركب ٥ أشخاص وفي المحطة قبل الأخيرة ركب شخص واحد ونزل ٤ أشخاص فكم شخصا أصبح في الحافلة؟


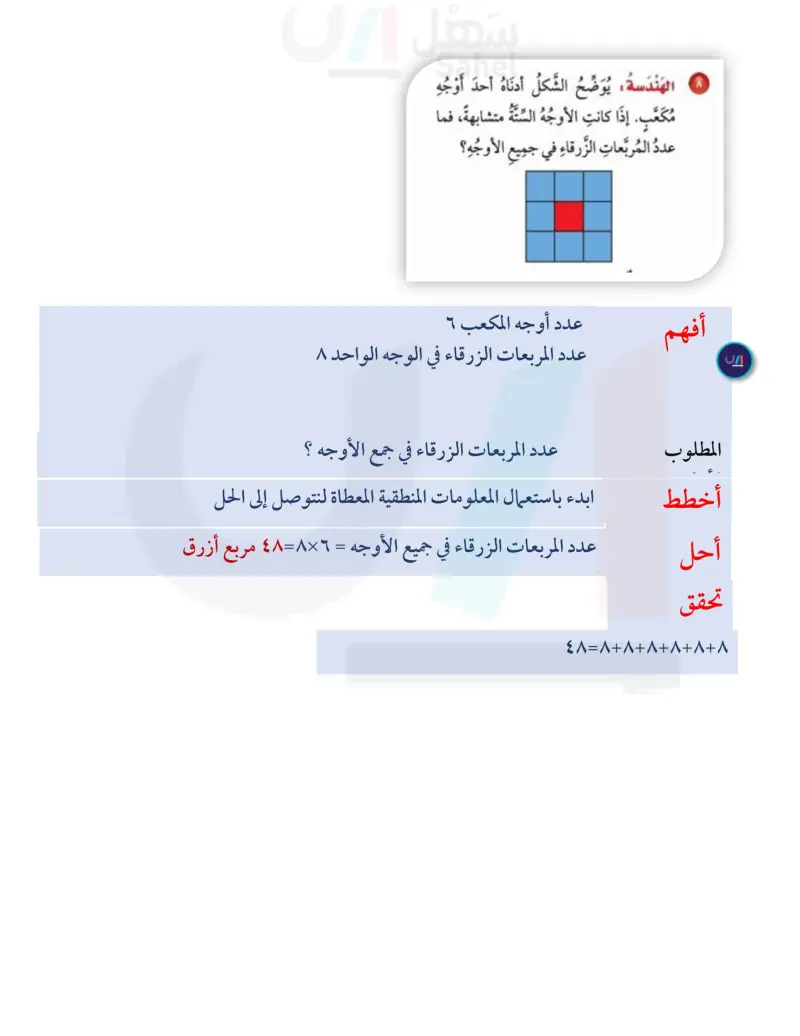
يوضح الشكل أدناه أحد أوجه مكعب إذا كانت الأوجه الستة متشابهة فما عدد المربعات الزرقاء في جميع الأوجه؟


يهوى كل من علي وعمر لعب كرة القدم وكرة تنس الطاولة والسباحة فكم ترتيباً لتلك الألعاب يمكنهما القيام به؟





 1
1 

 1
1 
 2
2 

 6
6