تمثيل الدوال المثلثية بيانيا - رياضيات2-3 - ثاني ثانوي

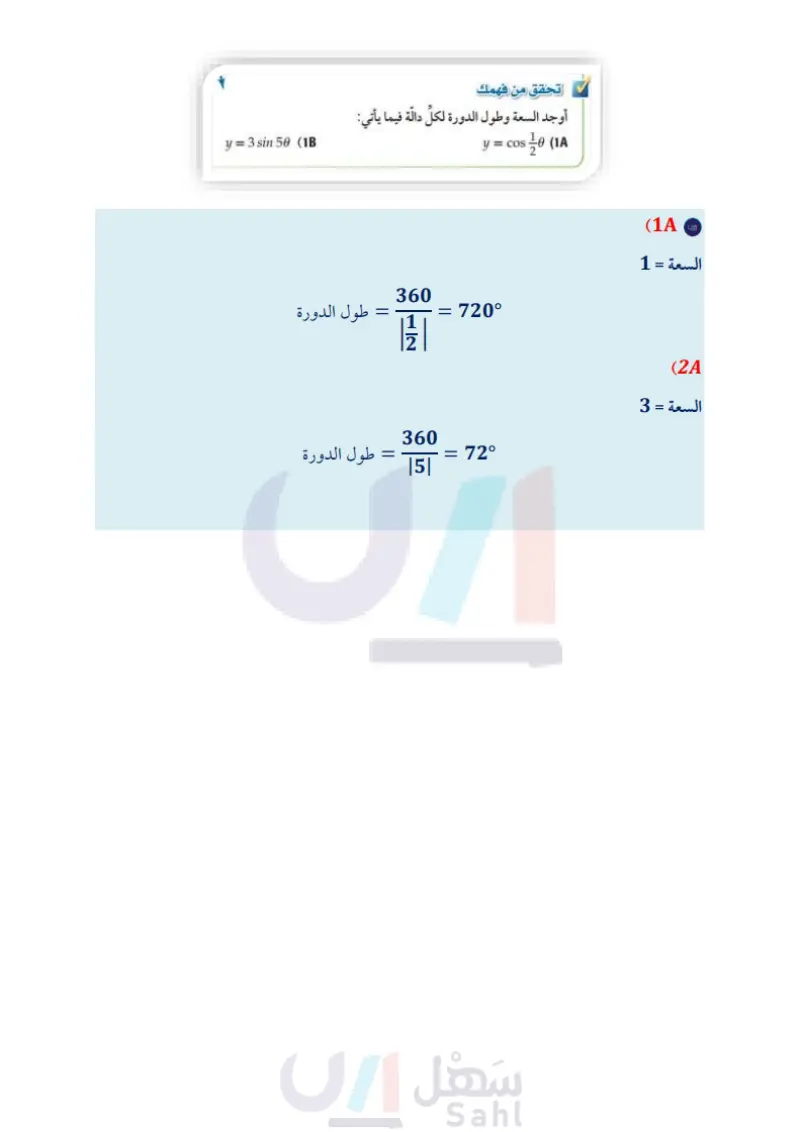
تمثيل الدوال المثلثية بيانيا رابط الدرس الرقمي www.ien.edu.sa Graphing Trigonometric Functions 8-7 فيما سبق درست الدوال الدورية. الدرس (6-8) وا الان . أصف دوال الجيب وجيب التمام والظل، وأمثلها بيانيا. لماذا؟ الموجات الضوء المرئية، أطوال موجات أو ترددات مختلفة. فاللون الأحمر له أكبر طول موجة واللون البنفسجي له أقصر طول موجة. ويمكنك تمثيل الحركة الموجية بالمعادلة: 2xx - y = Asin، حيث تمثل A سعة الموجة، طول الموجة. 入 m طول الموجة الأحمر طول الموجة دوال الجيب وجيب التمام والظل يمكنك تمثيل الدوال المثلثية بيانيًا في المستوى الإحداثي. تذكر أن أصف دوال مثلثية أخرى، منحنيات الدوال الدورية فيها أنماط متكررة أو دورات. وأن الطول الأفقي لكل دورة يُسمّى طول الدورة. وأمثلها بيانيا. اللمفردات السعة amplitude سعة منحنى دالة الجيب أو دالة جيب التمام تساوي نصف الفرق بين القيمة العظمى والقيمة الصغرى للدالة. | مفهوم أساسي الدالة المولدة (الأم) دالتا الجيب وجيب التمام y = sin 0 y = cos 0 أضف الي مطويتك الدورة Lycos |- الدورة y sin e 0 900 180270360 4500 5400 90 1827060450549 التردد frequency التمثيل البياني قراءة الرياضيات المجال مجموعة الأعداد الحقيقية مجموعة الأعداد الحقيقية المدى السعة طول الدورة (y-1≤ y ≤ 1} 1 360° {y | -1 = y = 1} 1 360° رمز طول الموجة يُستعمل الرمز للدلالة على طول الموجة، ويُقرأ لمبدا. إرشادات للدراسة طول الدورة في الدالتين: y = a sin b0, ، y = a cos bo ما تُمثل عدد الدورات "360. ففي المثال 1 يدل العدد 3 في الدالة: 30 y = 4 cos على وجود 3 دورات في 360 مما يعني وجود دورة واحدة في 120. يمكنك تطبيق ما تعلمته في أثناء دراستك لتحويلات التمثيل البياني للدوال الأخرى على التمثيل البياني للدوال المثلثية في صورتها العامة: y = a sin by = a cos b0، التي سعتها lal، وطول دورتها . مثال 1 إيجاد السعة وطول الدورة أوجد السعة وطول الدورة للدالة 30 y = 4 cos . السعة من الرسم نصف الفرق بين القيمة العظمى والقيمة 4-(-4) 2 الصغرى للدالة يساوي 4 = - أو طول الدورة 120 = 360° 360° Ты |3| من الرسم يكرر الرسم نفسه كل 120 تحقق من فهمك 360° Ты الدورة = 4 cos 30 ΛΙ AMAA 90 180 210 3600 1a1= 141 = 4 أوجد السعة وطول الدورة لكل دالة فيما يأتي: وزارة التعليم Ministry of Education 2024-1446 y = 3 sin 50 (1B y = cos 10 (IA 100 الفصل 8 حساب المثلثات

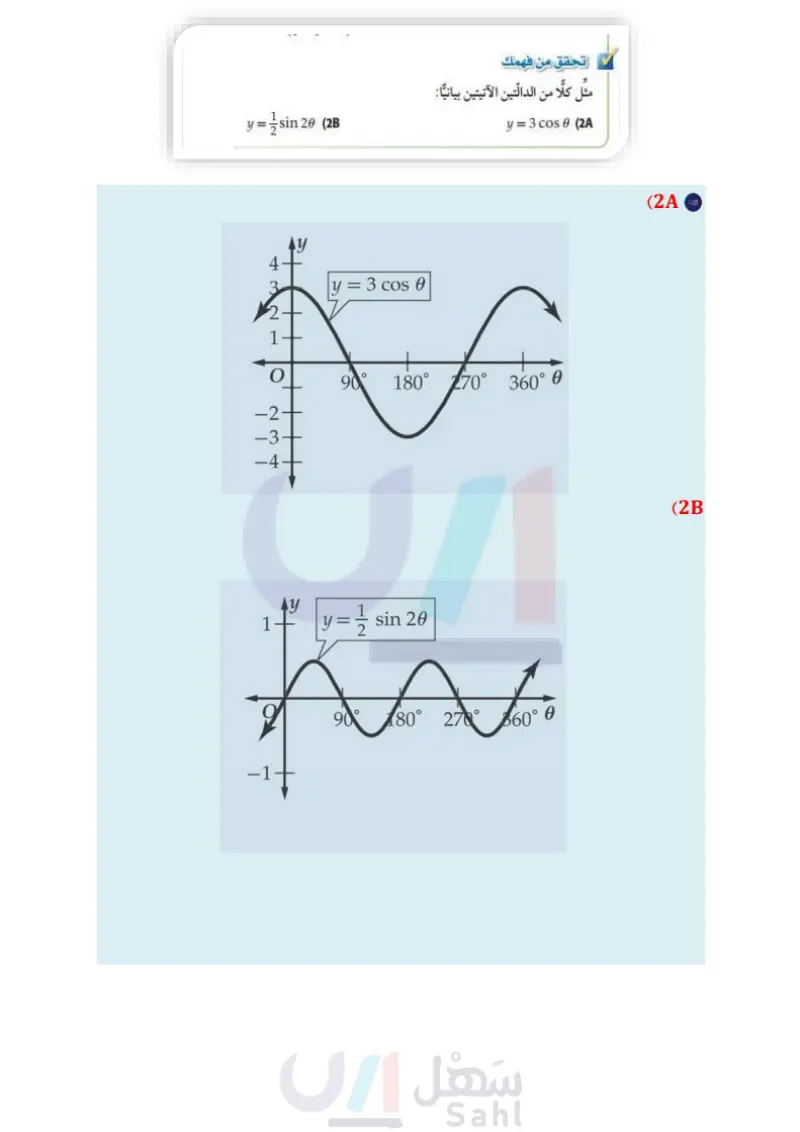
إرشادات للدراسة نقاط التقاطع مع المحور 6 يمكن إيجاد نقاط استعمل منحنيات الدوال المولدة (الأم) لتمثيل كل من الدالّتين : y = a sin bo y = a cos b0. ثم استعمل السعة وطول الدورة لرسم منحنى دالة الجيب أو دالة جيب التمام المناسبة بيانيا. ويمكنك أيضًا استعمال نقاط التقاطع مع المحور 6. إذا كانت دورة كل من الدالّتين y = a sin b و y = a cos b تبدأ عند 0 = 0 ، فإن نقاط تقاطع كل منهما مع تقاطع منحنى الدالة مع المحور 6 هي كما في الجدول الآتي: المحور 0 بوضع 0 = y وحل المعادلة أو إيجاد قيم 0 التي تحققها. y = a sin bo y=a cos be 1 360° 360° (0, 0), b b 20) (1 360° 4 b 0°, 0), (14/14 (3 360° إرشادات للدراسة السعة في التمثيل البياني لكل من الدالتين y = a sin bo, y = a cos be ، تكون السعة. هي lal ، والقيمة العظمي هي y = lal والقيمة الصغرى هي . y = - |a| مثال 2 تمثيل دالّتي الجيب وجيب التمام بيانيا مثل كلا من الدالّتين الآتيتين بيانيا : y = 2 sin 0 (a أوجد السعة، وطول الدورة، ونقاط التقاطع مع المحور 6 حيث: 1 = 2 = a . السعة : 2 = |2| = lal طول الدورة 360 = 360° 161 360° = |1| نقاط التقاطع مع المحور 0 هي: (00) y = cos 40 (b 360° b , 0) = (180°, 0) (360) = (360,00) - المنحنى يتسع رأسيا بحيث تكون القيمة العظمى 2 والقيمة الصغرى -2 . دورة واحدة طولها 360 . = 2 sin 0 90° 180° 270° 360° أوجد السعة، وطول الدورة، ونقاط التقاطع مع المحور ، حيث : 4 = a = 1, b . السعة 1= |1|= |a| طول الدورة : 90 = - 360° 141 =- 360° Ть نقاط التقاطع مع المحور 0 هي: (22.50) = تحقق من فهمك y = cos 40 1 AAAAA (360) 360° b 4 ,0) 360° = (67.5°, 0) , 0) = b 4 -2+ مثل كلا من الدالّتين الآتيتين بيانيا: y= 3 cos 0 (2A y-sin 29 (28 تفيد الدوال المثلثية في تمثيل المواقف الحياتية المرتبطة بالحركة الدورية، مثل الموجات الكهرومغناطيسية أو موجات الصوت. ويتم وصف هذه الأمواج عادة باستعمال التردد، وهو عدد الدورات في وحدة الزمن. ولإيجاد تردد التمثيل البياني لدالة نجد مقلوب طول الدورة، فمثلا إذا كان طول الدورة للدالة ثانية، فإن ترددها يساوي 100 دورة في الثانية. 100 وزارة التعليم الدرس - تمثيل الدوال المثلثية بيانيا 0 101 2024-1446

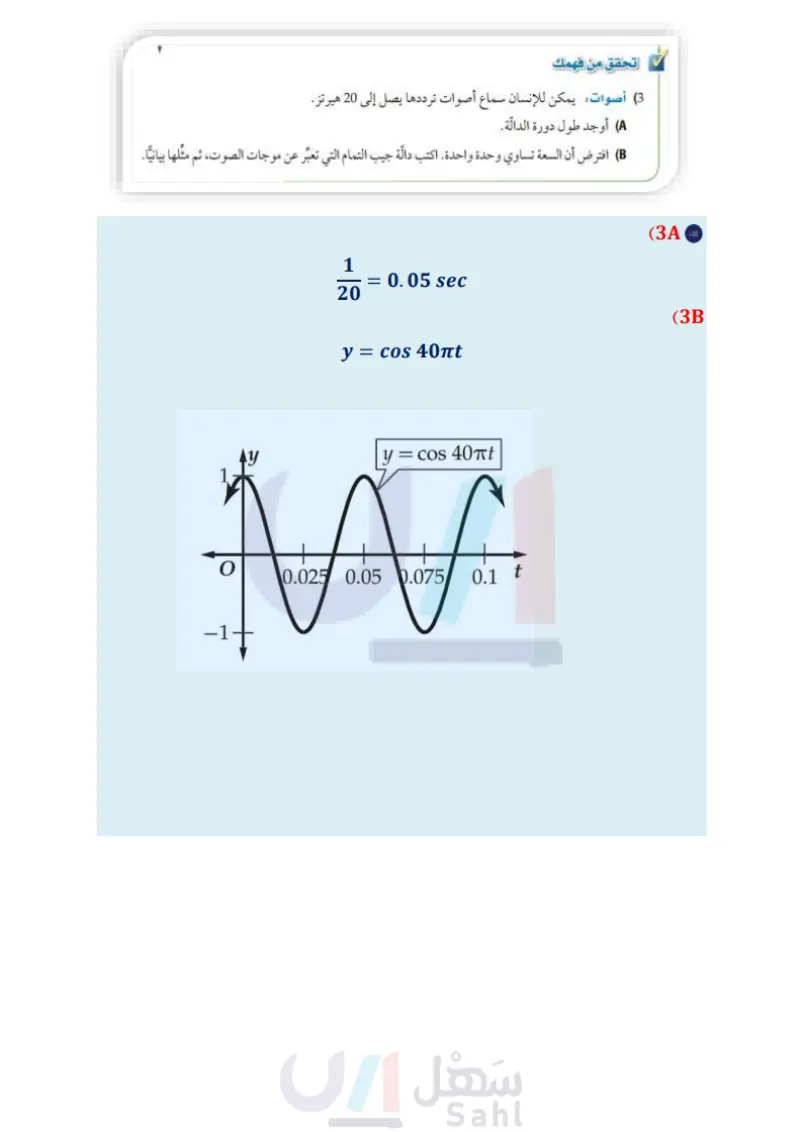
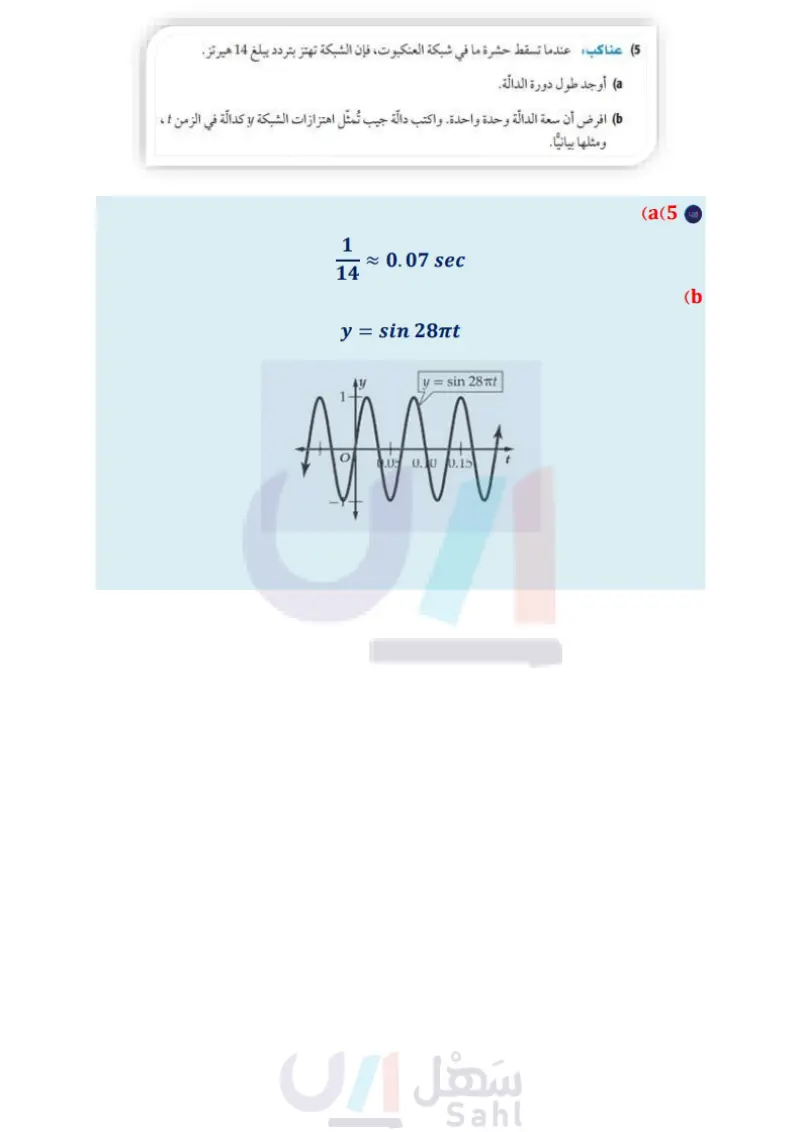
الربط بالحياة مثال 3 من واقع الحياة تمثيل موقف بدالة دورية أصوات تُسمى الأصوات التي يكون ترددها أقل من المستوى الذي يسمعه الإنسان، الأصوات تحت السمعية. ويمكن للفيلة سماع الأصوات تحت السمعية التي يصل ترددها إلى 5 هيرتز أو 5 دورات/ ثانية. a أوجد طول دورة الدالة التي تعبر عن موجات الصوت. يوجد 5 دورات في الثانية، وطول الدورة هو مقلوب التردد، ويساوي الزمن الذي تستغرقه دورة واحدة، لذلك فإن طول الدورة هو 0.2 = . ) افترض أن السعة تساوي وحدة واحدة. اكتب دالة جيب تُمثل موجة الصوت / باعتبارها دالة في الزمن ، ثم يمكن للفيلة سماع صوت يبعد عنها 5 أميال. ويمكن للإنسان سماع الأصوات التي يتراوح ترددها بين 20 هيرتز إلى 20000 هيرتز. مثلها بيات طول الدورة =- 27 161 27 = 0.2 161 0.2|| = 27 اكتب العلاقة بين طول الدورة و 6 عوض اضرب الطرفين في 161 اضرب الطرفين في 15 موجبة الصورة العامة لدالة الجيب y = sin 10mt b = 10π 0. A y = a sin bo 0.8 a = 1, b = 107, 0=t y = 1 sin 10mt بسط y = sin 10mt إرشادات للدراسة السعة وطول الدورة لاحظ أن السعة تؤثر في منحنى الدالة في اتجاه المحور ، أما طول الدورة فيؤثر في اتجاه المحور x . تحقق من فهمك أصوات يمكن للإنسان سماع أصوات ترددها يصل إلى 20 هيرتز أوجد طول دورة الدالة. افترض أن السعة تساوي وحدة واحدة. اكتب دالّة جيب التمام التي تعبر عن موجات الصوت، ثم مثلها بيانيا. تُعد دالة الظل من الدوال المثلثية التي لها خطوط تقارب. أضف إلى مطويتك التمثيل البياني للدالة الدورة مفهوم أساسي دالة الظل الدالة المولدة (الأم) المجال y = tan 0 y = tan 0 100 ± 90° +180°n, ne Z المدى مجموعة الأعداد الحقيقية السعة طول الدورة غير معرفة 180° طول الدورة لمنحنى الدالّة y = a tan be يساوي . لها تكون عند المضاعفات الفردية للعدد . 180° 161 102 الفصل 8 حساب المثلثات 180° Ты 90% 90° 270% 450° ، ولا يوجد سعة لهذه الدالة، وخطوط التقارب الرأسية وزارة التعليم Ministry of Education 2024-1446

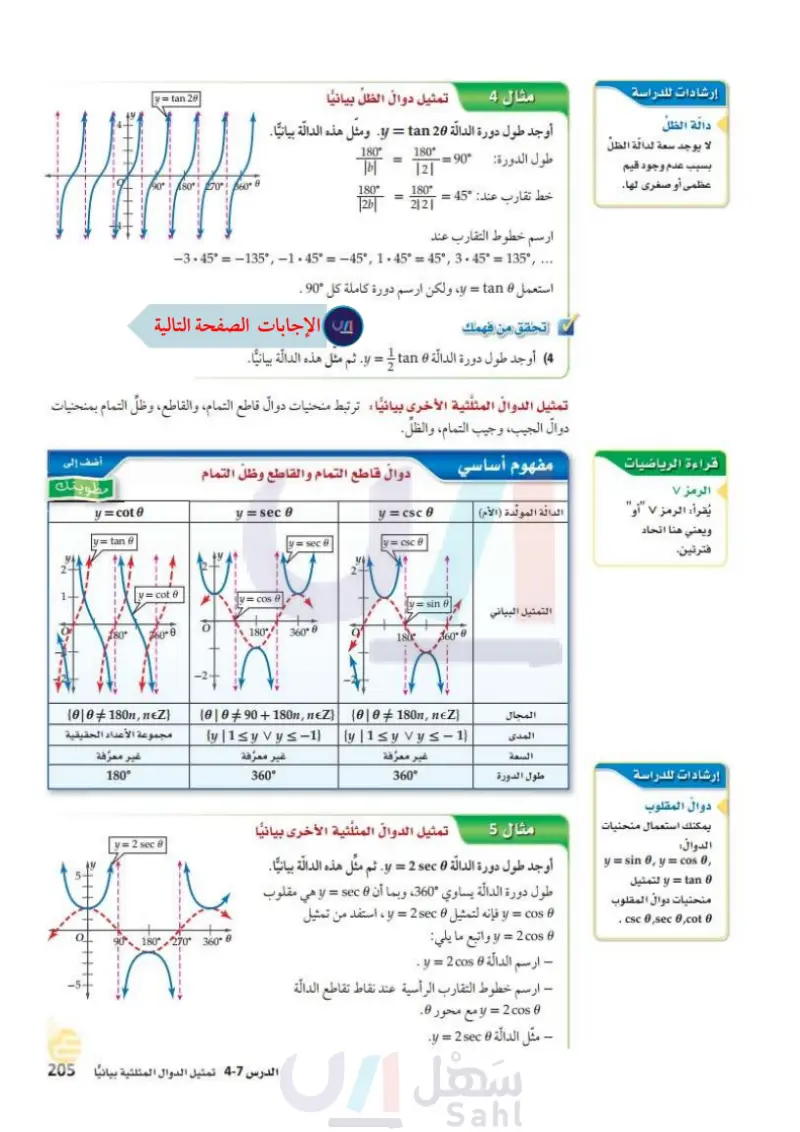
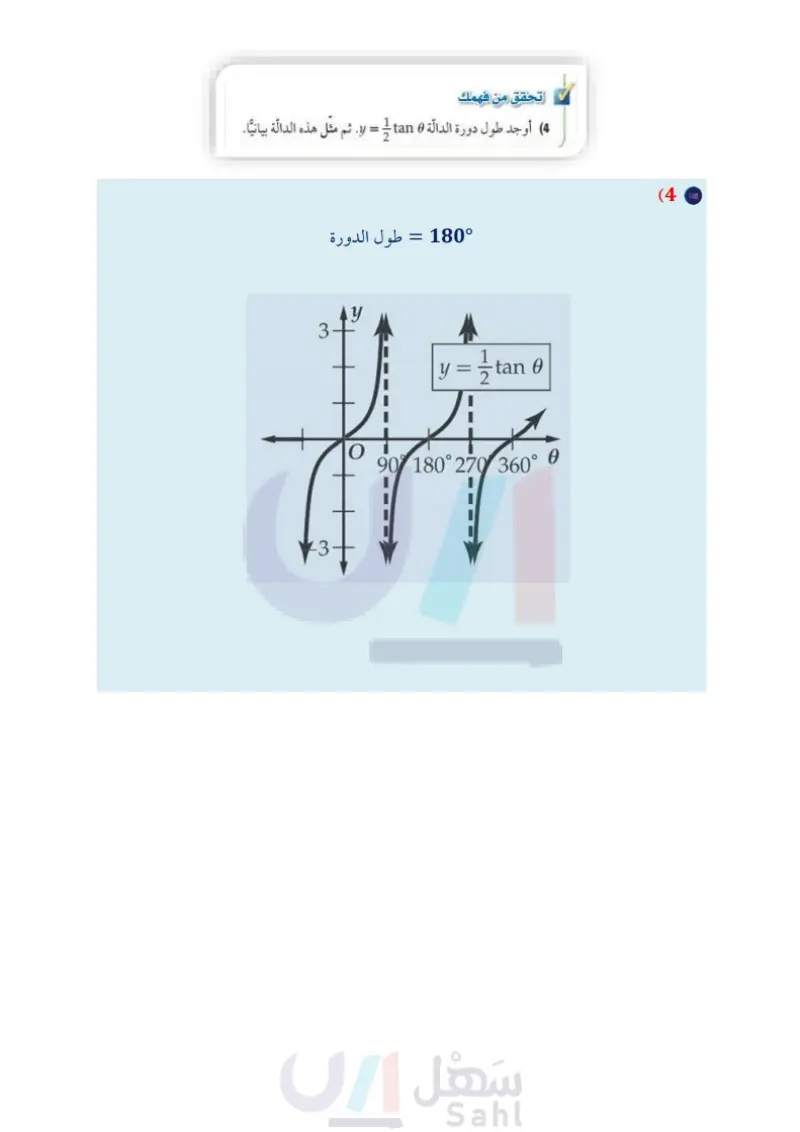
إرشادات للدراسة دالة الظل مثال 1 تمثيل دوال الظل بيانيا أوجد طول دورة الدالة 20 y = tan. ومثل هذه الدالة بيانيا. لا يوجد سعة لدالة الظل = 180° 121 بسبب عدم وجود قيم طول الدورة: 90 = . عظمى أو صغرى لها. خط تقارب عند : 45 = 180° 2121 180° = y = tan 20 (80°1 70° 60° 0 180° 2b ارسم خطوط التقارب عند =135°, -3.45°=-135°, -1.45° = -45°, 1.45° 45°, 3.45°=1 = قراءة الرياضيات الرمز ۷ يُقرأ: الرمز 7 "أو" ويعني هنا اتحاد فترتين. استعمل 6 y = tan، ولكن ارسم دورة كاملة كل °90 . تحقق من فهمك (4) أوجد طول دورة الدالة 0 y = A tan. ثم مثل هذه الدالة بيانيا. تمثيل الدوال المثلثية الأخرى بيانيًا ترتبط منحنيات دوال قاطع التمام والقاطع، وظل التمام بمنحنيات دوال الجيب، وجيب التمام، والظل. مفهوم أساسي الدالة المولدة (الأم) دوال قاطع التمام والقاطع وظل التمام y = sec 0 y = csc 0 V = sec 9 y=csc 8 أضف إلى مطويتك y = Cot o y = tan 0 180° y = cot 8 y= cos v = sin 8 60-0 0 180 360°0 1808 360-0 (010180n, neZ} مجموعة الأعداد الحقيقية غير معرفة 10 | 0 ± 90 + 180n, neZ} {y | 1 = y v y = -1} {0 | 0 + 180n, neZ y | 1 = y vy = - 1} غير معرفة غير معرفة 180° y = 2 sec 0 al 180 270° 360° 0 360° 360° التمثيل البياني المجال المدى السعة طول الدورة امثال تا تمثيل الدوال المثلثية الأخرى بيانيا أوجد طول دورة الدالة 6 y = 2 sec. ثم مثل هذه الدالة بيانيا. طول دورة الدالة يساوي 360، وبما أن 6 y = sec هي مقلوب y = cos فإنه لتمثيل 6 y = 2 sec ، استفد من تمثيل 0 y = 200s واتبع ما يلي: ارسم | الدالة 6 y = 2cos . - ارسم خطوط التقارب الرأسية عند نقاط y = 2 cos مع محور 0. - مثل الدالة 6 y = 2 sec . تقاطع ا الدالة وزارة التعليم الدرس - تمثيل الدوال المثلثية بيانيا 1030 2024-1446 إرشادات للدراسة دوال المقلوب يمكنك استعمال منحنيات الدوال y = sin 0, y = cos 6, 0 y = tan لتمثيل منحنيات دوال المقلوب .csc 0,sec 0,cot 0

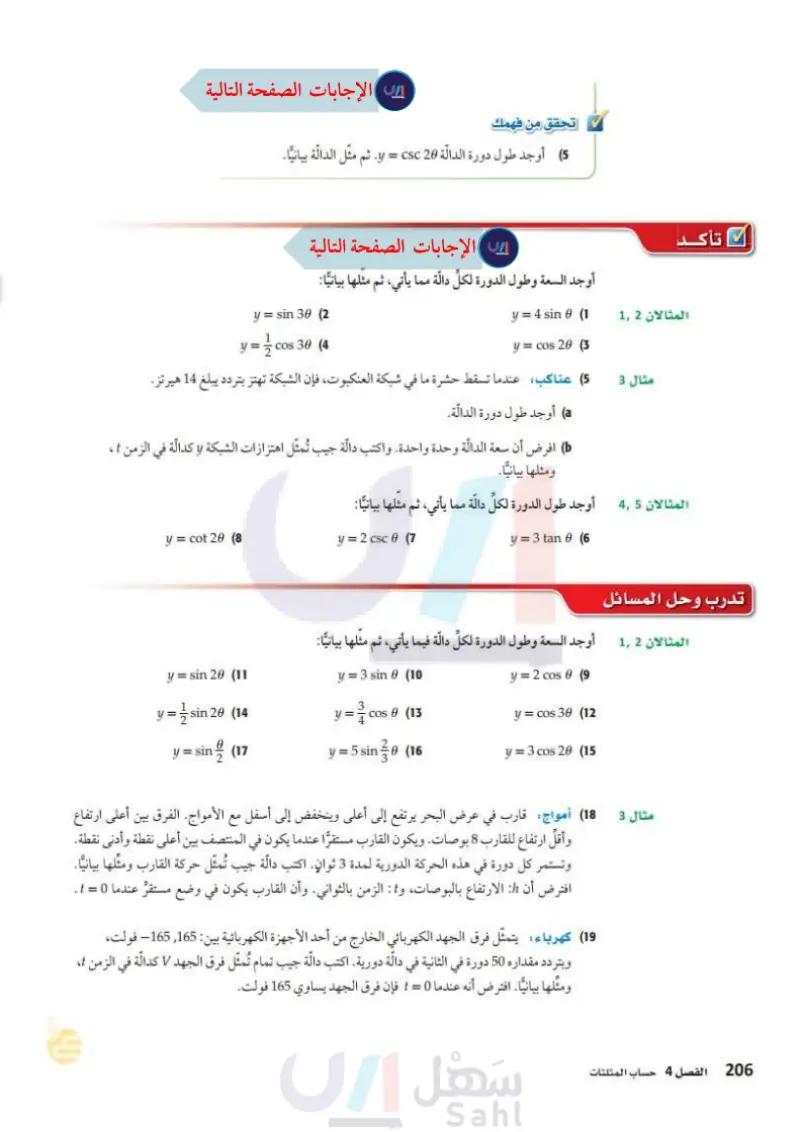
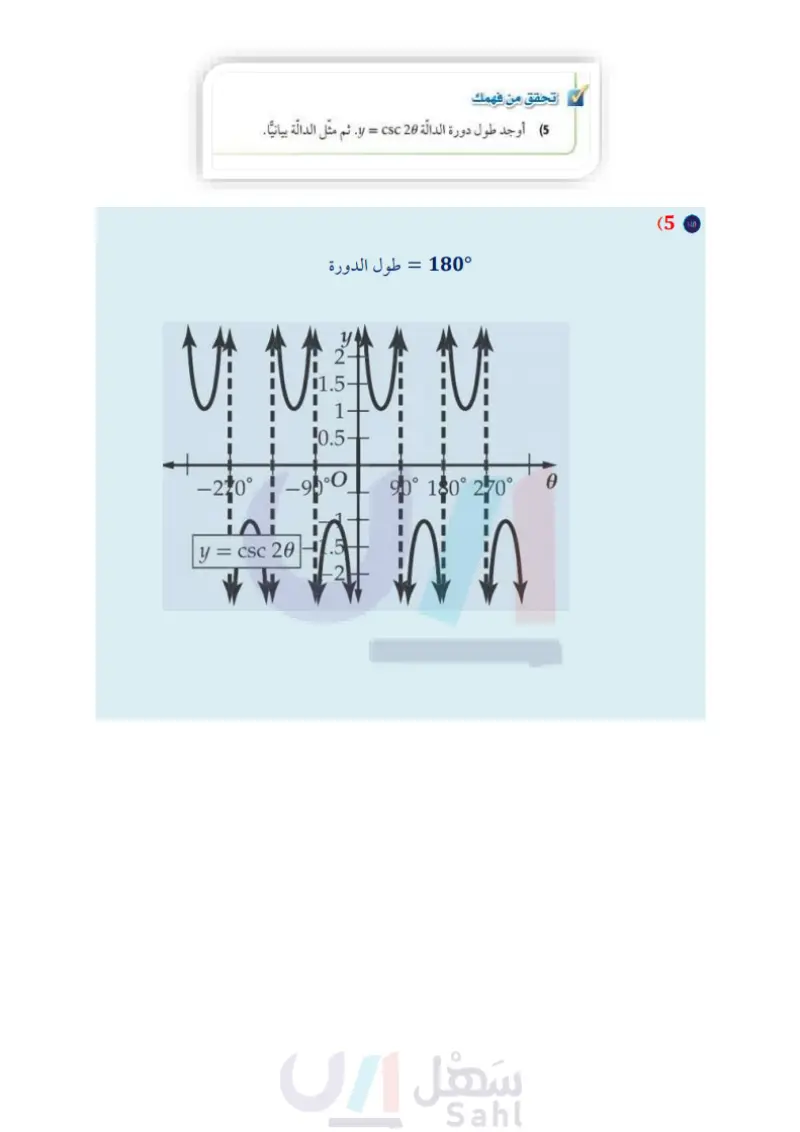
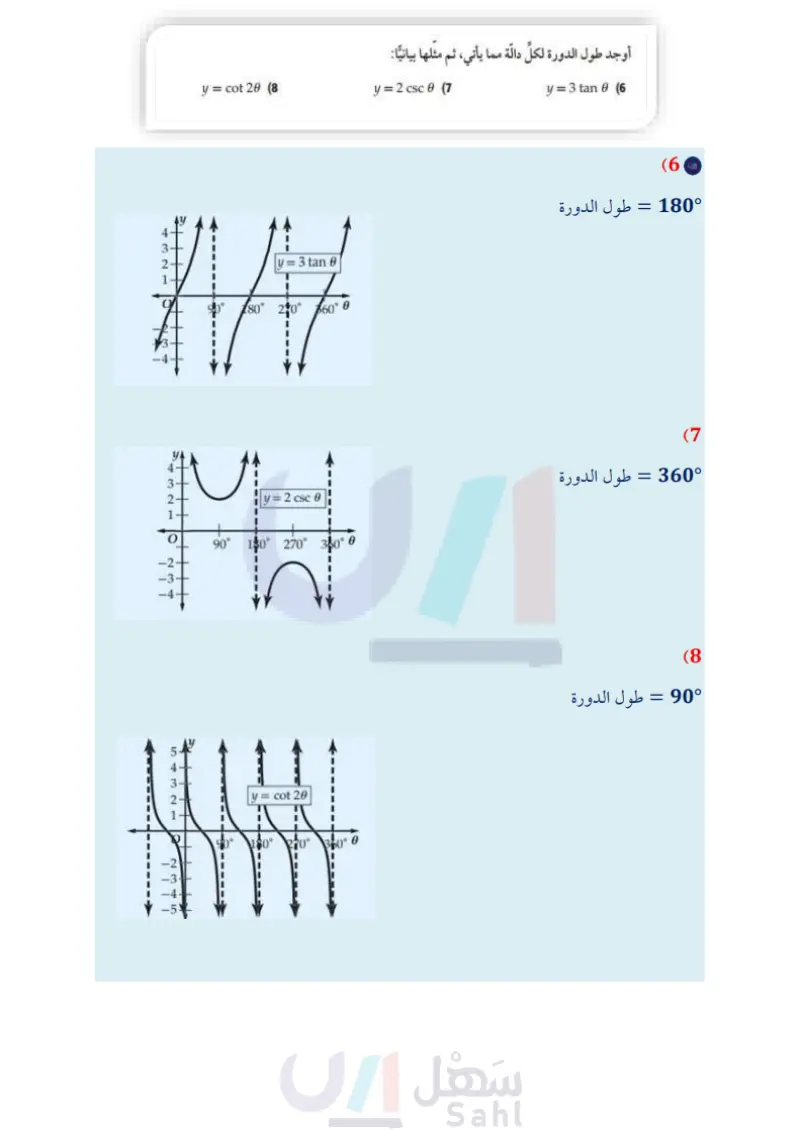
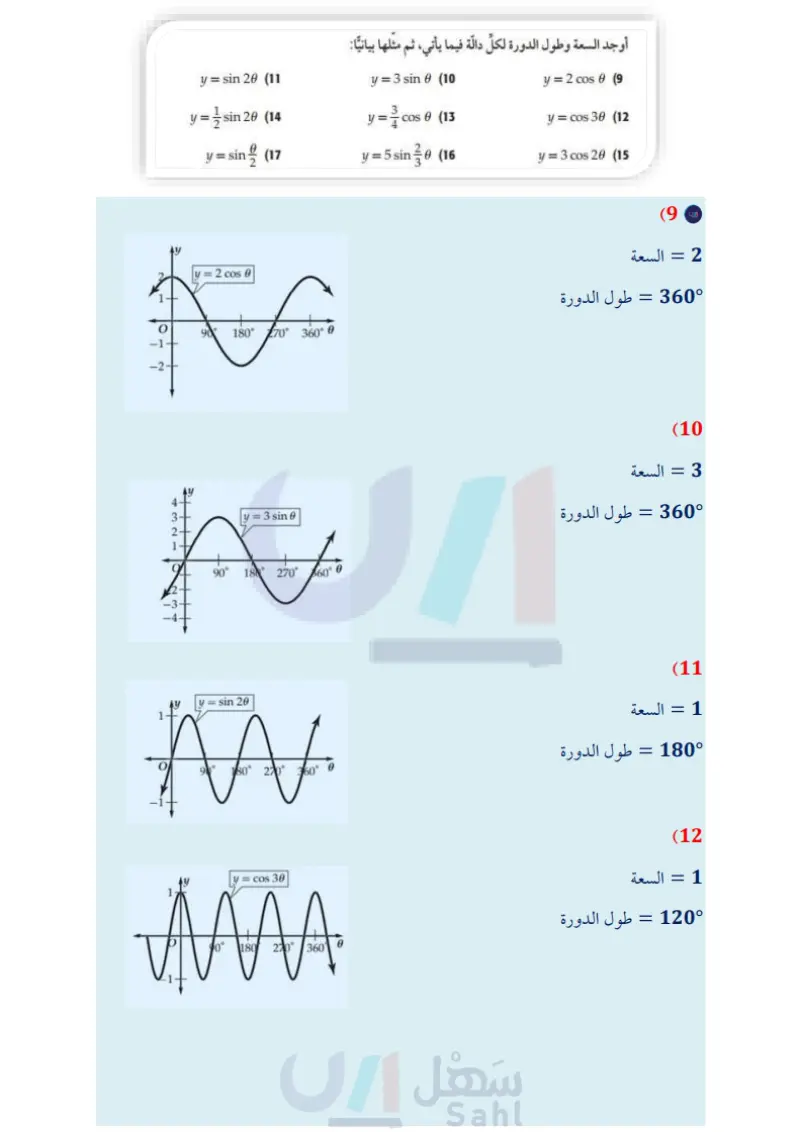
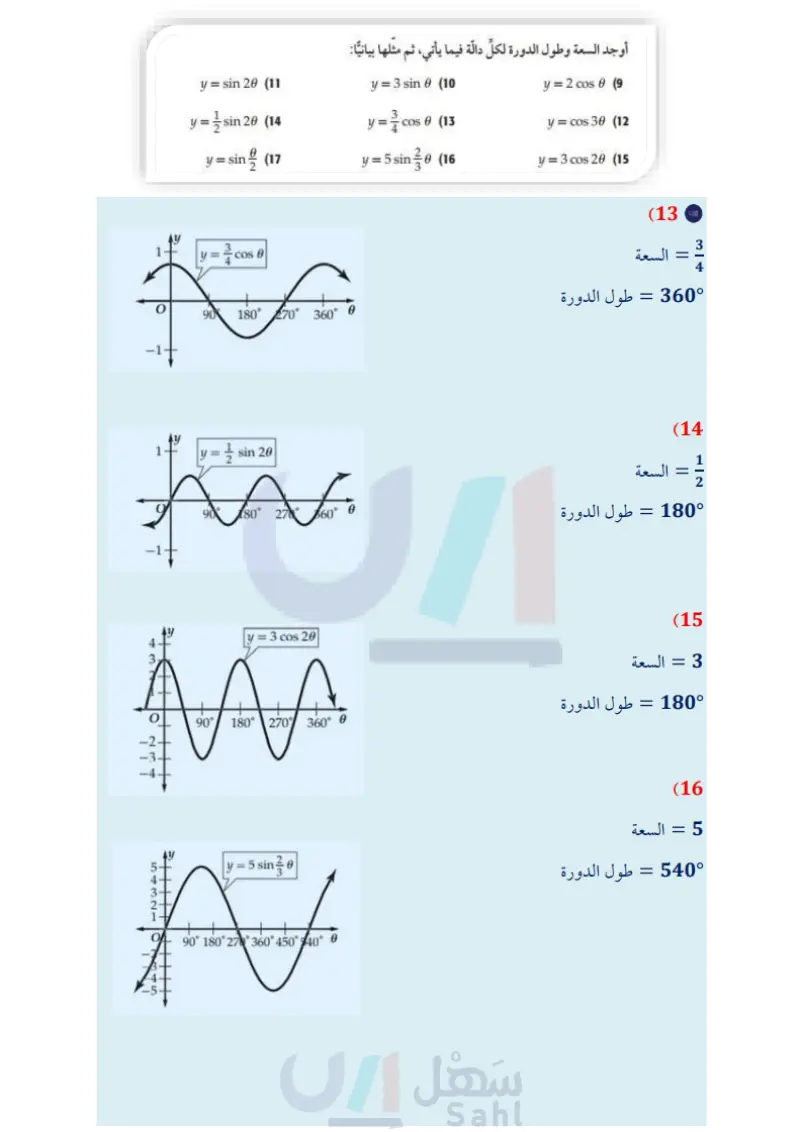
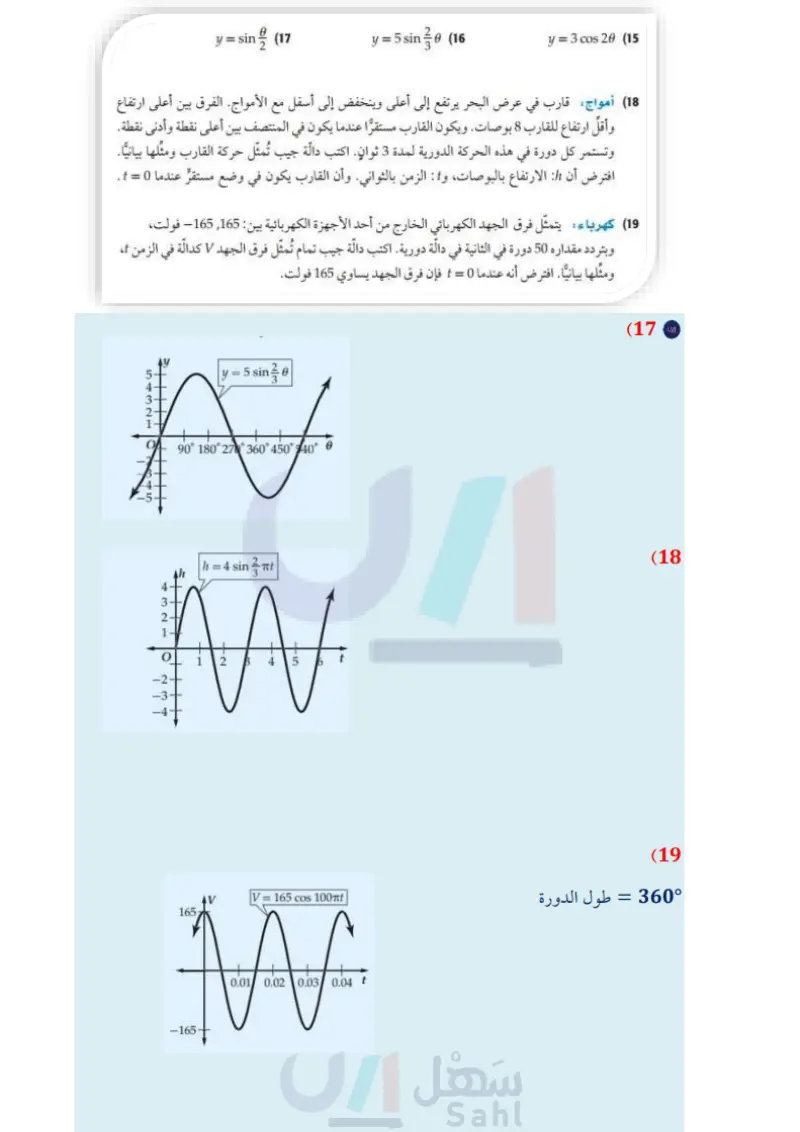
تأكد المثالان 1 تحقق من فهمك = CS ما أوجد طول دورة الدالة 20 و ثم مثل الدالة بيانيا. أوجد السعة وطول الدورة لكل دالة مما يأتي، ثم مثلها بيانيا: y = 4 sin 6 (1 y = cos 20 (3 y = sin 30 (2) y= .cos 30 (4 مثال 3 (5) عناكب عندما تسقط حشرة ما في شبكة العنكبوت، فإن الشبكة تهتز بتردد يبلغ 14 هيرتز. الله أوجد طول دورة الدالة. ) افرض أن سعة الدالة وحدة واحدة. واكتب دالة جيب تُمثل اهتزازات الشبكة و كدالة في الزمن ٤ ، ومثلها بيانيا. المثالان 45 الوجد طول الدورة لكل دالة مما يأتي، ثم مثلها بيانيا تدرب وحل المسائل y = 3 tan 6 (6 y = cot 20 (8 y = 2 csc 0 (7 المثالان 12 أوجد السبعة وطول الدورة لكل دالة فيما يأتي، ثم مثلها بيانيا : y = sin 20 (11 y = 3 sin 6 (10) y= 2 cos 0 (9 y = 3 sin 28 (14 y = cos 0 (13 y= cos 30 (12 y = sin (17 y = 5 sin 30 (16 y = 3 cos 20 (15 مثال 3 18 أمواج قارب في عرض البحر يرتفع إلى أعلى وينخفض إلى أسفل مع الأمواج. الفرق بين أعلى ارتفاع وأقل ارتفاع للقارب 8 بوصات. ويكون القارب مستقرا عندما يكون في المنتصف بين أعلى نقطة وأدنى نقطة. وتستمر كل دورة في هذه الحركة الدورية لمدة 3 ثوان. اكتب دالة جيب تُمثل حركة القارب ومثلها بيانيا. افترض أن : الارتفاع بالبوصات و الزمن بالثواني. وأن القارب يكون في وضع مستقر عندما 0 = t . 19) كهرباء يتمثل فرق الجهد الكهربائي الخارج من أحد الأجهزة الكهربائية بين : 165, 165 فولت، وبتردد مقداره 50 دورة في الثانية في دالة دورية. اكتب دالة جيب تمام تمثل فرق الجهد V كدالة في الزمن ، ومثلها بيانيا. افترض أنه عندما 0 = t فإن فرق الجهد يساوي 165 فولت 104 الفصل 8 حساب المثلثات وزارة التعليم Ministry of Education 2024-1446

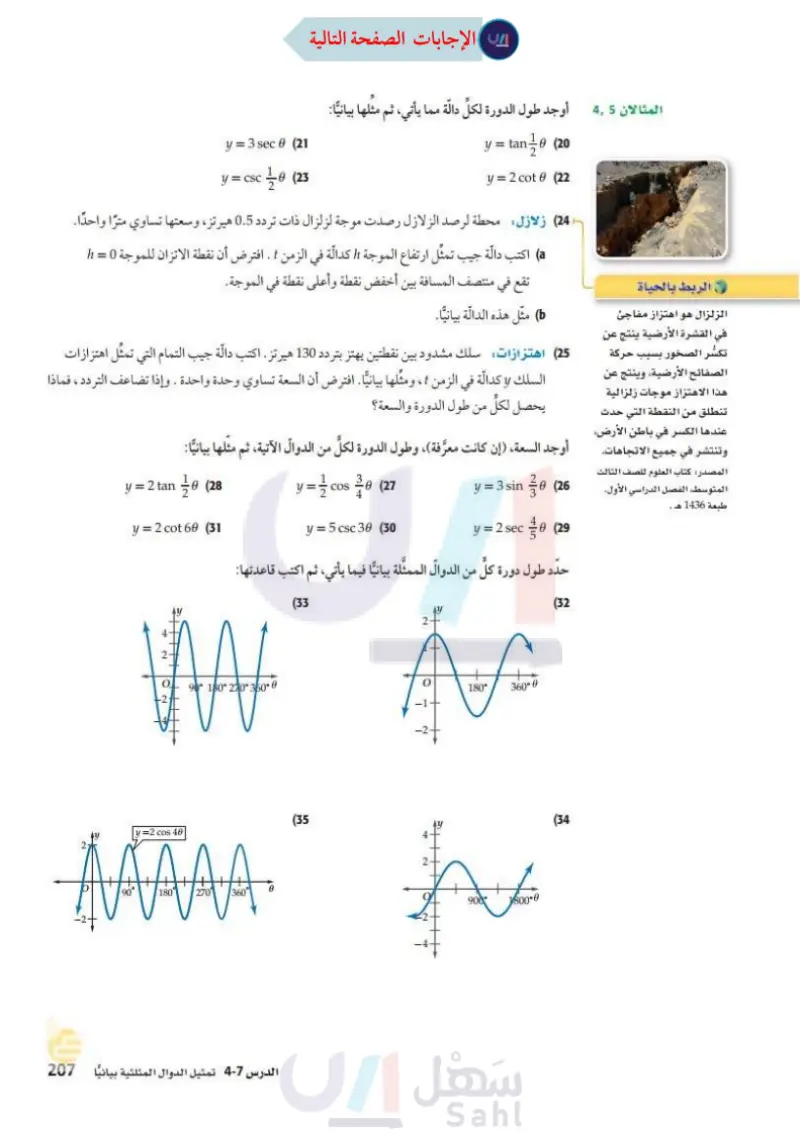
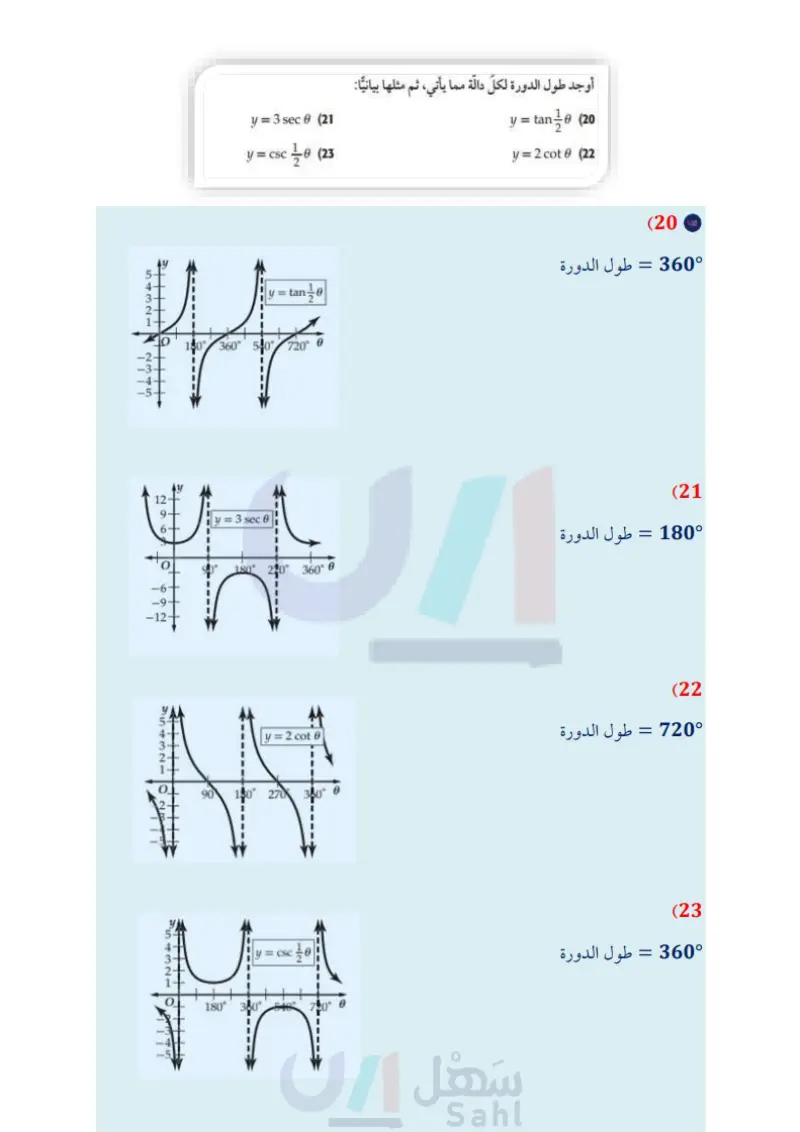
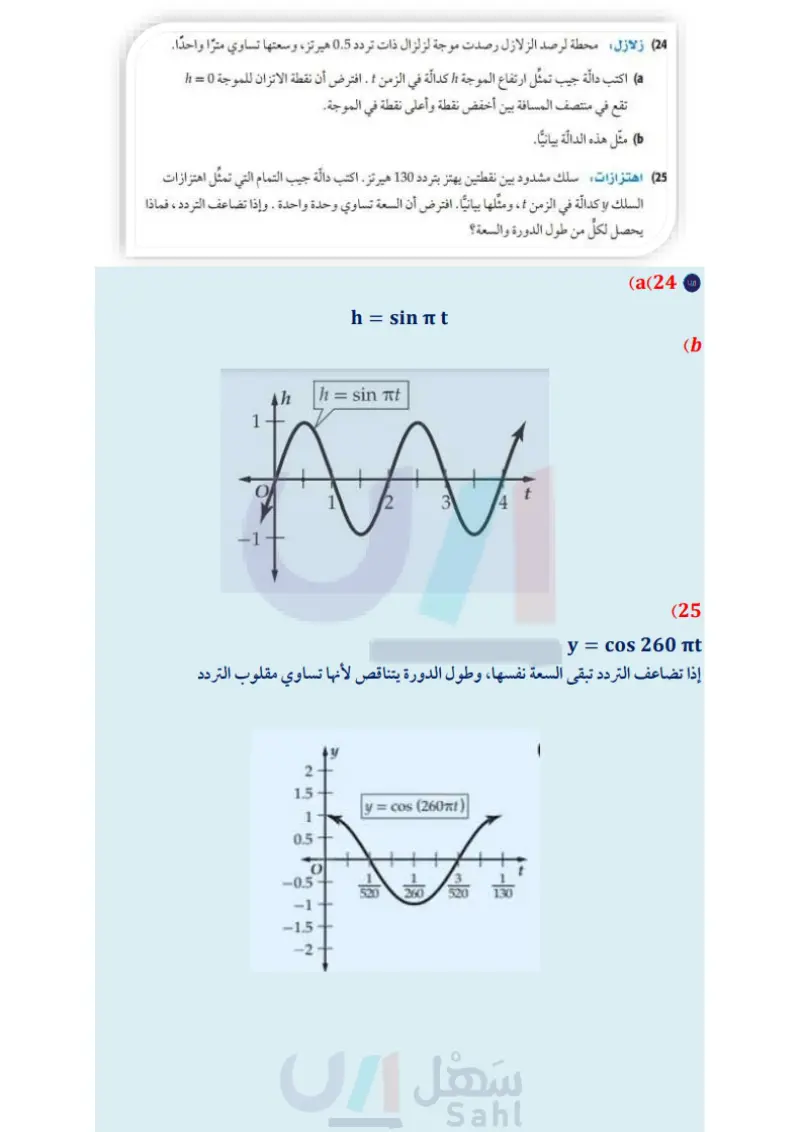
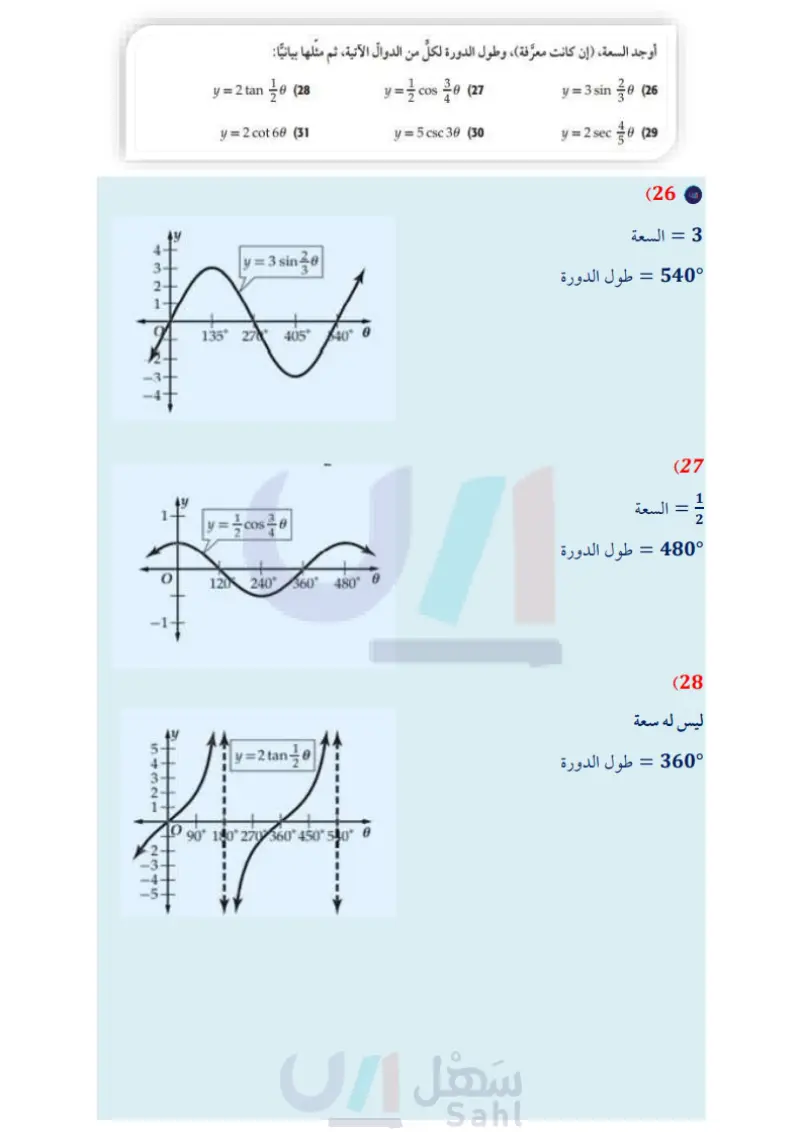
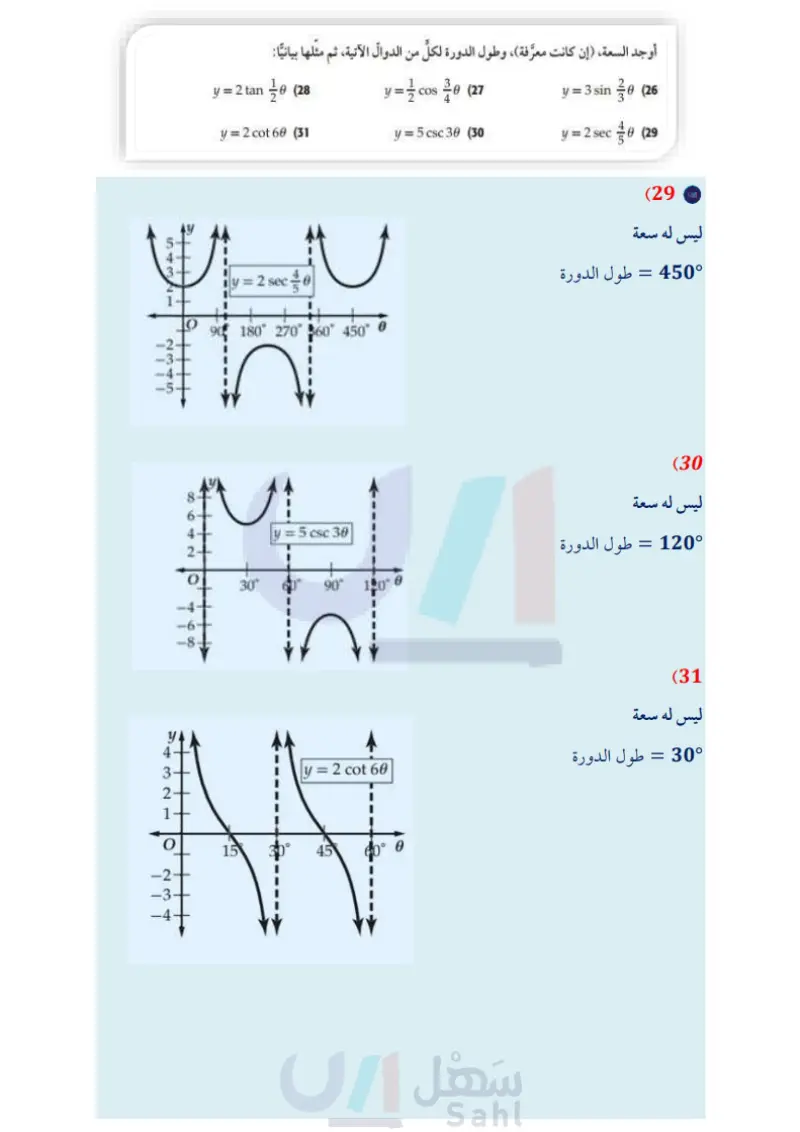
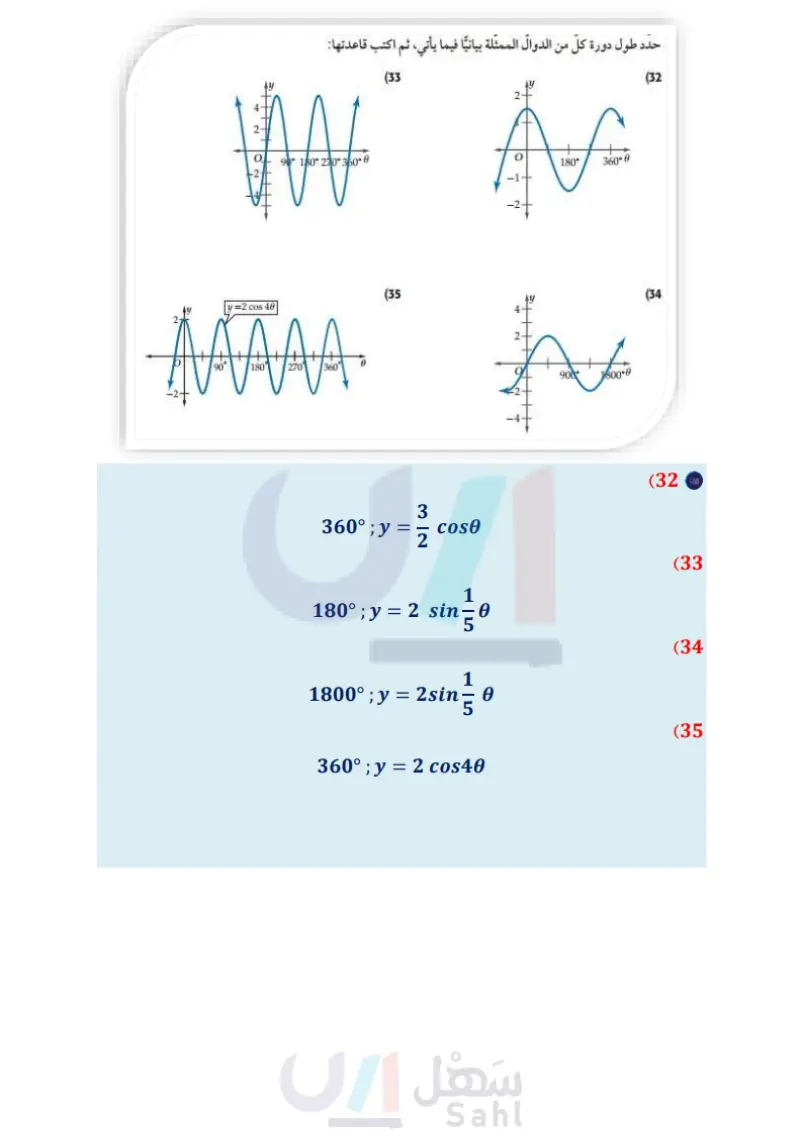
المثالان 45 أوجد طول الدورة لكل حالة مما يأتي، ثم مثلها بيانيا: y = tan 30 (20 y = 2 cot 6 (22) y = 3 sec 6 (21 y = csc 10 (23 الربط بالحياة الزلزال هو اهتزاز مفاجئ في القشرة الأرضية ينتج عن (24) زلازل محطة لرصد الزلازل رصدت موجة لزلزال ذات تردد 0.5 هيرتز، وسعتها تساوي مترًا واحدًا. a) اكتب دالة جيب تمثل ارتفاع الموجة كدالة في الزمن .. افترض أن نقطة الاتزان للموجة 0 = تقع في منتصف المسافة بين أخفض نقطة وأعلى نقطة في الموجة. مثل هذه الدالة بيانيا. تكسر الصخور بسبب حركة (25) اهتزازات سلك مشدود بين نقطتين يهتز بتردد 130 هيرتز . اكتب دالة جيب التمام التي تمثل اهتزازات الصفائح الأرضية، وينتج عن السلك لو كدالة في الزمن ، ومثلها بيانيا . افترض أن السعة تساوي وحدة واحدة ، وإذا تضاعف التردد ، فماذا هذا الاهتزاز موجات زلزالية يحصل لكل من طول الدورة والسعة؟ تنطلق من النقطة التي حدث عندها الكسر في باطن الأرض وتنتشر في جميع الاتجاهات. أوجد السعة، (إن كانت معرفة)، وطول الدورة لكل من الدوال الآنية، ثم مثلها بيانيا: المصدر كتاب العلوم للصف الثالث المتوسط الفصل الدراسي الأول. طبعة 1436 هـ . y-(27 y = 3 sin 30 (26 y = 5 csc 30 (30) y = 2 sec 06 (29 y = 2 tan 10 (28 y = 2 cot 60 (31 حدد طول دورة كلِّ من الدوال الممثلة بيانيا فيما يأتي، ثم اكتب قاعدتها : 2- ww 01 y=2 cos 40 W 90 180 270 350° AAAA. (33 (35 As 180° 360-0 for 900 1600-6 (32) (34 وزارة التعليم الدرس - تمثيل الدوال المثلثية بيانيا 0 105 2024-1446 Edu

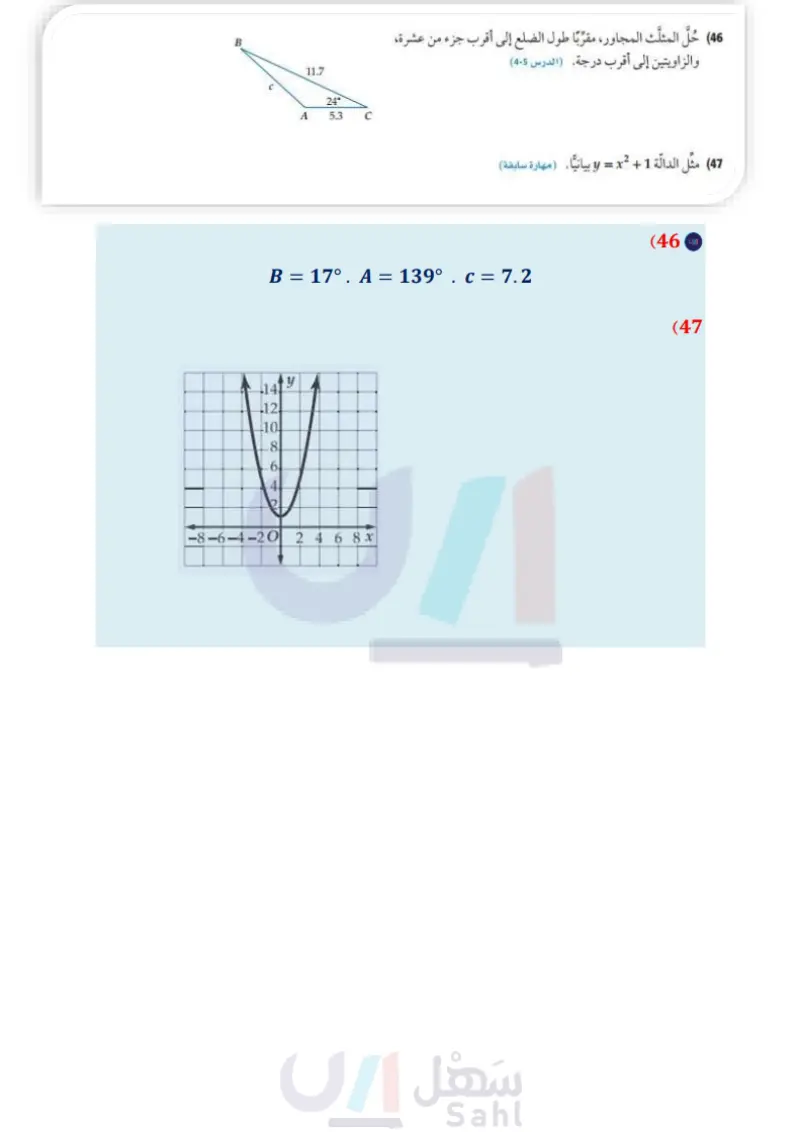
| تدريب على اختبار مسائل مهارات التفكير العليا 36) تحد، حدد المجال والمدى لكل من الدالتين 6 y = a sec 6 y = a cos حيث a عدد حقيقي موجب. 37) تبرير عين أوجه الشبه وأوجه الاختلاف بين منحنى الدالة 6 y = { sin ، ومنحنى الدالة 0 3 sin = / (38) مسألة مفتوحة : اكتب دالّة مثلثية سعتها 3 ، وطول دورتها "180. ثم مثلها بيانيا. (39) اكتب وضح كيف تُحسب سعة الدالة 0 y = 2 sin . ووضح كيف يؤثر المعامل السالب في التمثيل البياني للدالة (40) . 10) مراجعة أي من الزوايا الآنية تحلق لا - tan؟ = 6 1215° D 3 1080° B 1830° C 990° A (41) إجابة قصيرة: أوجد الحدّ رقم 100001 في المتتابعة: (42) إذا كان عدد سكان إحدى المدن قبل عشر سنوات يساوي 312430 نسمة، وعدد السكان الحالي يساوي 418270 نسمة، فما النسبة المئوية للزيادة في عدد السكان خلال السنوات العشر الماضية؟ 75% D 66% C 34% B 25% A y= وزارة التعليم Ministry of Education 2024-1446 13, 20, 27, 34, 41, ... 4 sin 4-2 cos(45 3(sin 45°)(sin 60°) (44 B 11.7 C 24° A 5.3 C مراجعة تراكمية أوجد قيمة كل مما يأتي: (الدرس (3-8) cos 120° sin 30° (43 46) حل المثلث المجاور، مقربًا طول الضلع إلى أقرب جزء من عشرة، والزاويتين إلى أقرب درجة (الدرس 5-8) 147 مثل الدالة للروبيائيا. (مهارة سابقة) + 106 الفصل 8 حساب المثلثات