الدوال المثلثية في المثلثات القائمة الزاوية - رياضيات2-2 - ثاني ثانوي
الفصل الخامس: العلاقات والدوال النسبية
الفصل السادس: المتتابعات والمتسلسلات
الفصل السابع: الاحتمالات
الفصل الثامن: حساب المثلثات
نشاط الفصل الخامس: العلاقات والدوال النسبية
نشاط الفصل السادس: المتتابعات والمتسلسلات
نشاط الفصل السابع: الاحتمالات
8-1 الدوال المثلثية في المثلثات القائمة الزاوية رابط الدرس الرقمي Trigonometric Functions in Right Triangles الماذا؟ www.ien.edu.sa فيما سبق درست استعمال نظرية فيثاغورس في إيجاد أطوال يعتمد ارتفاع الشخص في التزلُّج الهوائي على طول حبل السحب ) والزاوية " التي يصنعها الحبل مع الخط الأفقي. وإذا علمت هاتين أضلاع مثلثات قائمة الزاوية (مهارة سابقة) القيمتين، يمكنك استعمال نسبة معينة لإيجاد ارتفاع المتزلج. والان الارتفاع أجد قيم الدوال المثلثية الدوال المثلثية للزوايا الحادة يُعرف حساب المثلثات بأنه دراسة العلاقة : بين زوايا المثلث وأضلاعه. أستعمل الدوال المثلثية وتقارن النسبة المثلثية بين طولي ضلعين في المثلث القائم الزاوية، أما الدالّة المثلثية فتعرف من خلال نسبة مثلثية. لزوايا حادة. لإيجاد أطوال أضلاع وقياسات زوايا مثلثات يُستعمل الرمز الإغريقي ) ( ويُقرأ ثيتا) عادة للدلالة على قياس زاوية حادة في قائمة الزاوية. الالمقران انشا حساب المثلثات trigonometry النسبة المثلثية trigonometric ratio الدالة المثلثية trigonometric function sine جيب التمام cosine الظل tangent قاطع التمام cosecant القاطع secant ظل التمام cotangent المثلث ، القائم الزاوية. حيث يُستعمل الوتر والضلع المقابل للزاوية التي قياسها 6 والضلع المجاور لها في تعريف الدوال المثلثية الست. مفهوم أساسي الوتر A الضلع المقابل الضلع المجاور C 0 B جميع الدوال المثلثية في مثلث قائم الزاوية بنك أضف إلى التعبير اللفظي: إذا كانت 0 تمثل قياس زاوية حادة في مثلث قائم الزاوية، فإن الدوال المثلثية الست تعرف بدلالة الوتر والضلع المقابل والضلع المجاور. المقابل الوتر = جيب (0) 0 sin المجاري - ، تمام 0 0 cos = ( ظل ) 0 tan الوتر الرموز المقابل (قاطع تمام 0 0 csc الوتر المجاور : ( قاطع 0 0 sec الوتر المجاور = ظل تمام (0) 8 cot المقابل المجاور المقابل أمثلة: sin 0 = cos = tan 6 = 5 csc 0 = sec 6 = cot 0 3 دوال المقلوب reciprocal functions معكوس الجيب inverse sine معكوس جيب التمام inverse cosine مثال 1 إيجاد قيم الدوال المثلثية إذا كانت تمثل قياس زاوية حادة في المثلث القائم الزاوية في ، فأوجد قيم الدوال المثلثية الست الزاوية 6 عندما يكون: طول الضلع المقابل للزاوية 0 : 8 = BC، طول الضلع المجاور للزاوية 0 : 15 = AC، طول الوتر : 17 = AB معكوس الظل inverse tangent زاوية الارتفاع angle of elevation زاوية الانخفاض angle of depression تحقق من فهمك 8 15 15 = المقابل المجاور المجاور المقابل 15 tan 0 = 17 17 cot 0 = 15 = المجاور الوتر الوتر المجاور 8 = cos 0= 17 17 sec 6 = 8 المقابل الوتر الوتر المقابل sin 0 = csc 0 = ) أوجد قيم الدوال المثلثية الست للزاوية 8 الواردة أعلاه. وزارة التعليم الدرس 1- الدوال المثلثية في المثلثات القائمة الزاوية 570 2024-1446

قراءة الرياضيات تسمية المثلثات تستعمل الأحرف الكبيرة لاحظ أن النسب: قاطع التمام والقاطع، وظلّ التمام، هي مقلوب النسب الجيب، وجيب التمام، والظل على الترتيب. وتُستعمل في تعريف دوال المقلوب. حيث يمكن تعريفها على النحو الآتي: cot 0 = 1 tan 0 sec 6 = cos 0 CSC 0 = sin 0 مجال أي دالة مثلثية هو مجموعة قياسات الزوايا الحادة 6 في المثلث القائم الزاوية؛ لذا فإن قيم الدوال المثلثية تعتمد فقط على قياسات الزوايا الحادة وليس على أطوال أضلاع المثلث القائم الزاوية؛ أي أنَّ قيم الدوال المثلثية للزاوية الحادة ستبقى كما هي مهما اختلفت أطوال أضلاع المثلث. (مثال2 إيجاد النسب المثلثية خلال هذا الفصل للدلالة B زاوية حادة في مثلث قائم الزاوية ، إذا كان } = sin B ، فأوجد قيمة tan B. على رؤوس المثلث وقياسات زوايا الرؤوس ويُستعمل الحرف الصغير المقابل للحرف الكبير الخطوة 1 ارسم مثلثا قائم الزاوية وسم إحدى زواياه الحادة B . المقابل بما أن . الوتر = بـ 5، والوتر بـ 8 . . = sin B . فحدد على الرسم طول الضلع المقابل 5 للدلالة على طول الضلع المقابل للزاوية، وتتضح الخطوة 2 استعمل نظرية فيثاغورس لإيجاد ) . دلالة الحرف من السياق. نظرية فيثاغورس a 8 بسط b = 5, c = 8 a² + b² = c² a²+5² = 82 a²+25=64 a² = 39 = ±√√39 a = a = √√39 الخطوة 3 أوجد قيمة tan B . اطرح 25 من كلا الطرفين خذ الجذر التربيعي لكلا الطرفين الطول لا يمكن أن يكون سالبا تاريخ الرياضيات اكتشف علماء العرب المسلمون العديد من العلاقات في حساب المثلثات، واستعملوها في حل المعادلات، وإيجاد ارتفاع الشمس وعمل الجداول الرياضية، ويرجع المقابل المجاور 5 √39 tan B=- = 5 √39 39 تحقق من فهمك (2) إذا كان = tan B ، فأوجد قيمة sin B . دالة الظل عوض عن المقابل بـ 5 والمجاور بـ أنطق المقام إليهم الفضل في جعله علما تتكرر الزوايا التي قياساتها 30,560 كثيرًا في حساب ! مستقلا عن علم الفلك. ومن أبرز هؤلاء العلماء : البيروني ( أبو الريحان محمد بن أحمد البيروني (362-439 هـ)). الطوسي ( نصر الدين الطوسي (597-672 هـ) ). الكاشي ( غياث الدين بن مسعود الكاشي ( توفي سنة 839 هـ ) ) . البتاني ( ابن عبد الله بن محمد بن سليمان الحراني (235-316هـ) ). مفهوم أساسي 60° 2x المثلثات. √39 بعض قيم الدوال المثلثية للزوايا الخاصة نستنتج من المثلث الذي قياسات زواياه 90-60-30 أن: tan 30° = 3 30° tan 60° = V3 13 45° x√√2 x sin 30° = = 를 cos 30°= sin 60 = cos 60° = 2 نستنتج من المثلث الذي قياسات زواياه 90-45-45 أن: tan 45° = 1 أضف إلى مطوينك sin 450 = √2 cos 45° = √2 2 58 الفصل 8 حساب المثلثات 45° x B وزارة التعليم Ministry of Education 2024-1446

قراءة الرياضيات
تاريخ الرياضيات
استعمال الدوال المثلثية: يمكنك استعمال الدوال المثلثية لإيجاد أطوال الأضلاع المجهولة وقياسات الزوايا المجهولة في مثلث قائم الزاوية مثال 3 إيجاد طول ضلع مجهول استعمل دالّة مثلثية لإيجاد قيمة x ، م مقربًا إلى أقرب جزء من عشرة. طول الوتر يساوي 8 والطول المجهول هو الضلع المجاور للزاوية 30 . استعمل دالة جيب التمام لإيجاد قيمة x . 30° x المجاور الوتر إرشادات للدراسة اختيار دالة إذا كان طول الوتر مجهولا فإنه يجب استعمال دالة الجيب أو جيب التمام لإيجاد دالة. القيمة المجهولة. COS = دالة التمام جيب عوض عن 6 بـ 30 ، المجاور بـ X الوتر بـ 8 cos 30° = √3 cos 30° = 2 اضرب كلا من الطرفين في 8 8√√3 =x 6.9 x اتحقق من فهمك استعمل الآلة الحاسبة استعمل دالّة مثلثية لإيجاد قيمة x. قرب إلى أقرب جزء من عشرة. (3A x 60° 14 (3B 45° I 10 الربط بالحياة يمكنك استعمال الآلة الحاسبة لإيجاد أطوال الأضلاع المجهولة في المثلثات التي لا تتضمن زواياها أياً من الزوايا: 30,560 . مثال ا إيجاد طول ضلع مجهول بناية لحساب ارتفاع بناية مشى أحمد مسافة ft 200 مبتعدا عن قاعدة البناية. واستعمل أداة (مقياس زاوية الميل) لقياس الزاوية المحصورة بين خط نظره المار مقاييس زاوية الميل تستعمل بقمة البناية والخط الأفقي. إذا كان مستوى نظره على ارتفاع ft 5، فما ارتفاع البناية؟ لقياس زاوية ميل المجال الزاوية المقيسة كما يوضّح الشكل هي 76. طول الضلع المجاور لها ft 200، المغناطيسي الأرضي ودرجة الضلع المجهول طوله هو الضلع المقابل لها. استعمل دالة الظل لإيجاد ) . ميل واهتزاز المركبات والقوارب والطائرات. كما 76° + .200 ft 5 ft تستعمل في رصد البراكين المقابل المجاور وحفر الآبار. tan 0 = d tan 76° = 200 200 tan 76° = d 802 = d دالة الظل عوض عن 0 بـ 76 ، والمقابل بـ ) ، والمجاور بـ 200 اضرب الطرفين في 200 استعمل الآلة الحاسبة للتبسيط بما أن مقياس زاوية الميل كان على ارتفاع ft 5 عن سطح الأرض ، فإن ارتفاع البناية يساوي ft 807 تقريباً. وزارة التعليم الدرس 1- الدوال المثلثية في المثلثات القائمة الزاوية 59 2024-1446

اختيار دالة
مقاييس زاوية الميل تستعمل لقياس زاوية ميل المجال المغناطيسي الارضي ودرجة ميل واهتزاز المركبات
قراءة الرياضيات تحقق من فهمك 4 بنايات في الشكل المجاور بنايتان ارتفاع إحداهما 18m، وارتفاع الأخرى 37m، ولقياس المسافة الأفقية بينهما، وَضَعَ سعد أداة (مقياس زاوية الميل) على قمة البناية الصغرى، فوجد أن قياس الزاوية المحصورة بین الخط الأفقي بين البنايتين والخط المار من الأداة إلى قمة البناية الكبرى هو "25. فما المسافة الأفقية بين البنايتين؟ 118 m 37 m معكوس النسب المثلثية عند حل معادلات مثل 27 = 3x، تستعمل العملية العكسية للضرب. كما يمكنك استعمال معكوس الجيب أو تقرأ العبارة sin-1 x جيب التمام أو الظل في إيجاد قياسات الزوايا. معکوس جيب ، وتعني: الزاوية التي جيبها x يشبه هذا الرمز رمز الدالة العكسية (f-1 (x. كن حذرا ولا تخلط هذا الرمز مع رمز الأس ي مفهوم أساسي معكوس النسب المثلثية إذا كانت A زاوية حادة وجيبها يساوي ، فإن التعبير اللفظي: معكوس جيب x هو قياس 24 . أضف الى مطويتك السالب sin 1 sin x الرموز مثال: إذا كان sin A = x ، فإن : sin-1 x = m LA . sin A = 1 + sin-1 1 = m LA → m LA = 30° التعبير اللفظي : إذا كانت 4 زاوية حادة وجيب التمام لها يساوي x، فإن: معكوس جيب تمام X هو قياس 4 . الرموز مثال: إذا كان cos A = x ، فإن : cos-1 x = m LA . cos A=- -- cos-1. √2 2 =mZA mZA = 45° 2 التعبير اللفظي: إذا كانت A زاوية حادة وظلها يساوي ، فإن: معكوس ظل X هو قياس 4 . إذا كان tan A = x ، فإن : tan - 1 x = MLA . الرموز إرشادات للدراسة مثال: استعمال الآلة الحاسبة لإيجاد sin-16 10 tan A√√3 tan¹ √√3 = mLA →mLA = 60° = -> إذا علمت الجيب، أوجيب التمام أو الظل لزاوية حادة، فإنه يمكنك استعمال الحاسبة لإيجاد قياس هذه الزاوية باستعمال الآلة الحاسبة والذي هو معكوس النسبة المثلثية المعلومة. اضغط على المفاتيح 60 الآتية بالترتيب من اليسار إلى اليمين SHIFT sin (6 10 مثال تا إيجاد قياس زاوية مجهولة أوجد قياس كل زاوية مما يأتي مقربا إلى أقرب جزء من عشرة ZN (a Cos-1.81 16 ستحصل على الإجابة 36.9 ، ولإيجاد. اضغط على المفاتيح بما أنك تعرف طول الضلع المقابل للزاوية N وطول الوتر. استعمل دالة الجيب. SHIFT cos (8 +16- وستحصل على الإجابة 60 الفصل 8 حساب المثلثات sin N = 10 sin-1_6 =mZN 10 36.9° = mLN المقابل الوتر sin 0 = معكوس الجيب استعمل الآلة الحاسبة M N 6 10 L وزارة التعليم Ministry of Education 2024-1446

قراءة الرياضيات
استعمال الالة الحاسبة
18 x" A 16 cos 0= C 8 B المجاور الوتر معكوس جيب التمام استعمل الآلة الحاسبة ZB (b استعمل دالة جيب التمام. 8 cos B = 16 COS-1 8 16 =mZB 60° =mZB تحقق من فهمك أوجد قيمة ، مطرنا إلى أقرب جزء من عشرة (5B 27 15 (SA 17 إرشادات للدراسة في الشكل المجاور، تستى الزاوية المحصورة بين خط نظر السابع إلى المنقل والخط الأفقي له زاوية الارتفاع. كما تسمى زوايا الارتفاع والانخفاض الزاوية المحصورة بين خط نظر المنقذ إلى السابح والخط زاويتا الارتفاع والانخفاض للحالة الواحدة متطابقتان لأنهما زاويتان داخليتان متبادلتان لخطين متوازيين . الأفقي له زاوية الانخفاض. مثال 6 استعمال زوايا الارتفاع والانخفاض زاوية انخفاض 36 ft a لعبة الجولف : يقف لاعب جولف أسفل تل، وينظر إلى الحفرة في القمة. إذا كان ارتفاع التل 36ft، وزاوية ارتفاع أسفل التل عن الحفرة هي 12 فأوجد المسافة من أسفل التل إلى الحفرة. اكتب معادلة باستعمال دالة مثلثية تتضمن نسبة الارتفاع الرأسي (الضلع المقابل للزاوية (12) إلى المسافة من أسفل التل إلى الحفرة (الوتر). زاوية ارتفاع المنقذ 60° 195 ft المقابل الوتر sin 0=- اضرب : كلا من الطرفين في X 36 sin 12° = x x sin 12° = 36 36 x= الربط بالحياة أكثر العربات الدوارة انحدارا في العالم لها زاوية انحدار انخفاض) تقارب 90 . sin 12° x = 173.2 اقسم كلا من الطرفين على 12 sin استعمل الآلة الحاسبة لذا فإن المسافة من أسفل التلّ إلى الحفرة تساوي: 173.2ft تقريباً. العربة الدوارة قياس زاوية انحدار انخفاض) جزء من مسار عربة دوارة في إحدى مدن الألعاب هي 60 وينحدر هذا المسار من ارتفاع رأسي مقداره 195ft أوجد طول هذا الجزء من المسار. اكتب معادلة باستعمال دالّة مثلثية تتضمّن نسبة الارتفاع الرأسي (الضلع المقابل للزاوية 60) إلى طول الجزء من المسار (الوتر). 195 sin 60° = x x sin 60° = 195 x = 195 sin 60° x = 225.2 sin 0 = المقابل الوتر اضرب كلا من الطرفين في X اقسم كلا من الطرفين على 60 sin استعمل الآلة الحاسبة لذا فإن طول هذا الجزء من المسار يساوي 225.2ft تقريباً. وزارة التعليم الدرس 1- الدوال المثلثية في المثلثات القائمة الزاوية 61 of 2024-1446

زوايا الارتفاع والانخفاض
اكثر العربات الدوارة انحدارا في العالم لها زاوية انحدار (انخفاض)تقارب 90
32° 1.2 m 4m تحقق من فهمك (6) تفريغ حمولة : استُعمل سطح مائل لتفريغ شاحنة بزاوية ارتفاع قياسها 32. إذا كان ارتفاع السطح عند باب الشاحنة عن الأرض 1.2m، فأوجد طول السطح المائل. (68) سلالم : سُلَّم طوله 4m يستند إلى جدار منزل بزاوية ارتفاع قياسها 72، ما ارتفاع قمة السلم عن الأرض؟ مثال 1 أوجد قيم الدوال المثلثية الست للزاوية 0 الموضحة في كل مما يأتي: 16 12 (2 (1 6 مثال 2 معتبرا 24 زاوية حادة في مثلث قائم الزاوية، أجب عما يأتي: 3) إذا كان = cos A ، فما قيمة sin A؟ 4) إذا كان 2 = tan A، فما قيمة cos A؟ مثال 3 استعمل دالة مثلثية لإيجاد قيمة x في كلّ ممَّا يأتي مقربا إلى أقرب جزء من عشرة: x (7 7 33° 70° 100 ft 6 16 (11 x (5) 52° 6 60° x 22 مثال 4 8 أشجار يقف عبد الله ملاصقا لإحدى شجرتين متقابلتين في حديقة. إذا تحرك مبتعدا عن مكانه مسافة 100ft، في مسار عمودي على الخط الواصل بين الشجرتين، ومشكلا معهما زاوية قياسها 70 ، فما البعد بين الشجرتين ؟ مثال 5 أوجد قيمة x مقربًا إلى أقرب جزء من عشرة: 14 6 (10) 15 (9 مثال 6 (12) سلالم إذا علمت أن زاوية ارتفاع السلالم الموصى بها لمكافحة الحرائق هي °75، فإلى أي ارتفاع على بناية يمكن أن يصل سلم طوله 6.5m، إذا تم الاعتماد على زاوية الارتفاع الموصى بها، مقربا إلى أقرب جزء من عشرة؟ وزارة التعليم Ministry of Education 2024-1446 تأكد الفصل 8 حساب المثلثات 62

x 9 6 40 تدرب وحل المسائل مثال 1 أوجد قيم الدوال المثلثية السبت للزاوية 0 الموضحة في كل مما يأتي: (14 0 9 (16 0 12 0 13 (13 (15 10 مثال 2 إذا علمت أن AB زاويتان حادتان في مثلث قائم الزاوية، فأجب عما يأتي: (17) إذا كان = tan A، فما قيمة cos A (18) إذا كان لا = cos A، فما قيمة tan A؟ (19) إذا كان 3 = tan B، فما قيمة sin B (20) إذا كان و = sin B ، فما قيمة tan B؟ المثالان 34 في كل مما يأتي، استعمل دالة مثلثية لإيجاد قيمة x في كل مما يأتي، مقربا إلى أقرب جزء من عشرة. 30° 18 (23 (26) 70° 15 x 3.5m 250 ft 33° 3.1 m (22) 64° 4 32° 14 x (25 22 9 (21 x 48° 45 (24 (27) تزلج هوائي: ارجع إلى فقرة "لماذا؟“، واستعن بالمثلث إلى اليسار في إيجاد قيمة a التي تمثل ارتفاع المتزلج، إذا كان طول حبل السحب ft 250، وقياس الزاوية المحصورة بين الحبل والخط الأفقي يساوي 32، مقربًا إلى أقرب جزء من عشرة. 28) أرجوحة : يلعب طفل على أرجوحة في متنزه، فإذا كان ارتفاع أعلى الأرجوحة من الأرض 3.5m، والزاوية التي يصنعها حبل الأرجوحة مع الخط العمودي على الأرض في لحظة ما، كما هو مبين في الشكل المجاور، فأوجد ارتفاع مقعد الأرجوحة عن الأرض في تلك اللحظة. وزارة التعليم الدرس 1-1 الدوال المثلثية في المثلثات القائمة الزاوية 63 of 2024-1446

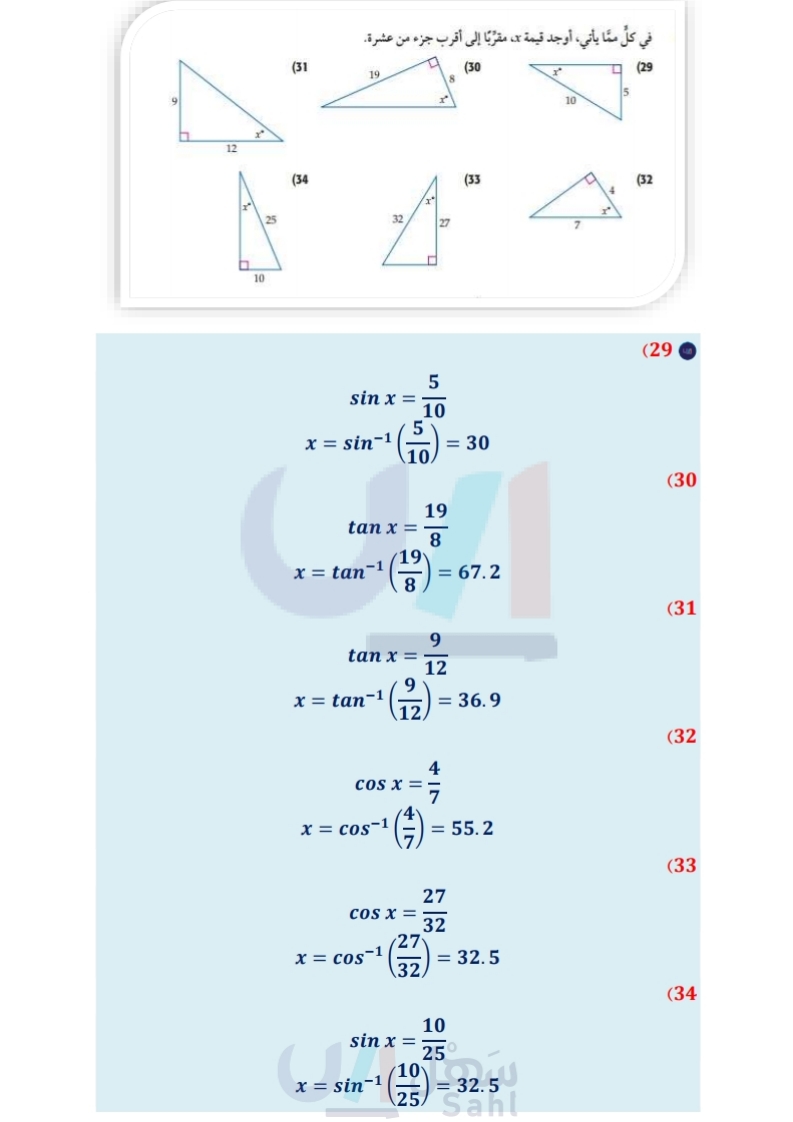
9 12 10 25 مثال في كل مما يأتي أوجد قيمة )، مقربا إلى أقرب جزء من عشرة 5 (31 19 (34 x" 32 27 (30 8 (33 (29) 5 10 7 4 (32 مثال 6 تسلق تسلّق أحد الأشخاص تلا بزاوية ارتفاع قياسها 20 أوجد ارتفاع الشخص عندما يكون قد قطع مسافة أفقية مقدارها m .18 . في كل مما يأتي، استعمل دوال مثالية، لإيجاد قيمة كل من 3.9 مقربا إلى أقرب جزء من عشرة. (38 4 81 50° (37 (36 30.2 71.8 x 46.5' y sin N = (40 sin T = 0.35 (42) cos Z = 0.98 (44) حُلَّ كلا من المعادلات الآتية: cos A = 3 (39 19 tan X = 15 (41 tan G = 0.125 (43) الربط بالحياة يستطيع الصقر رؤية أجسام طولها 10cm من km 1.5 كما أنه يستطيع رؤية الأشياء بوضوح عندما ينقض بسرعة 100 ميل/ الساعة. (45) أعشاش تنظر فاطمة نحو عُشُ طائر على شجرة بزاوية ارتفاع قياسها 74.5، فإذا كان مستوى نظرها يرتفع ft 5 عن سطح الأرض، وكانت تقف على بعد 12ft من قاعدة الشجرة، فما ارتفاع عُشّ الطائر عن سطح الأرض، مطرنا إلى أقرب قدم ؟ (46) صقور رأى صقر من ارتفاع ft 200 أرنبين A, B كما هو موضح في الشكل. ما المسافة التقريبية 2 بين الصقر والأرنب B؟ 6) ما البعد بين الأرنبين؟ 62° 72° 200 ft وزارة التعليم Ministry of Education 2024-1446 الفصل 8 حساب المثلثات 64

يستطيع الصقر رؤية اجسام طولها cm10 من 1.5km،كما انة يستطيع رؤية الاشياء بوضوح عندما ينقص بسرعة 109 ميل/الساعة.
في C ، AABC زاوية قائمة استعمل القيم المُعطاة لإيجاد أطوال الأضلاع المجهولة وقياسات الزوايا المجهولة في AABC، مقربًا إلى أقرب جزء من عشرة. mZB = 31°, b = 19 48 tan A= a=6 (50 mLA = 36", a = 12 (47) a=8, c = 17 (49 مسائل مهارات التفكير العليا (51) تحد قطعة مستقيمة تصل بين النقطتين (65) (2) كما هو موضح في الشكل المجاور، ما قياس الزاوية الحادة 6 المحصورة بين القطعة المستقيمة والمحور x ؟ وضح كيف وجدت القياس. (52) تبرير بين ما إذا كانت الجملة الآتية صحيحة أم خاطئة. وبرر إجابتك: قيمة دالة الجيب لأي زاوية حادة، لن تكون سالبة أبدا. y 7 6 B 5 1 2 3 4 5 6 7 x (53) إجابة مفتوحة في المثلث القائم الزاوية ABC، إذا علمت أن : sin A = sin C ، فماذا يمكن أن تستنتج عن هذا المثلث؟ برر إجابتك. 4- 3- 2 1- تدريب على اختبار (54) إذا كان ثمن شطيرة x ريالًا، وثمن علبة عصير لا ريالا، وثمن (55) نسبة طول مستطيل إلى عرضه هي 12:5 . إذا كانت مساحة المستطيل 2 240cm، فكم سنتمترا طول قطر المستطيل؟ شطيرتين مع علبة عصير 4.50 ريالات، وثمن ثلاث شطائر مع علبتي عصير 7.25 ريالات، فأي المصفوفات الآتية يمكن 4.50 7.25] ضربها في المصفوفة لا لإيجاد قيمة كل من x, y ؟ 26 A 28 B 30 C 32 D 3a2+6a+312a2-12 a2-3a-10 ÷ (58) 14c2f535cf4 ÷ (57 2-4 ga² 18ab3 (مهارة سابقة) 1 1 - + 4 8 16 - 1 + (60) 32 وزارة التعليم الدرس 1- الدوال المثلثية في المثلثات القائمة الزاوية 65 OF 2024-1446 C A 2 2 D B ] • | مراجعة تراكمية بسط كل حيارة مما يأتي: (مهارة سابقا) 15a2b2 14ac2 (56 6ab3 21ac أوجد مجموع حدود كل متسلسلة مما يأتي: 59 58 + ... + 13 + 8 + 8 (مهارة سابقة)




 0
0 

 0
0 

 2
2 

 0
0