القيم القصوى ومتوسط معدل التغير - رياضيات1-3 - ثالث ثانوي
الفصل الأول: تحليل الدوال
الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
كتاب النشاط
نشاط الفصل الأول: تحليل الدوال
نشاط الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية

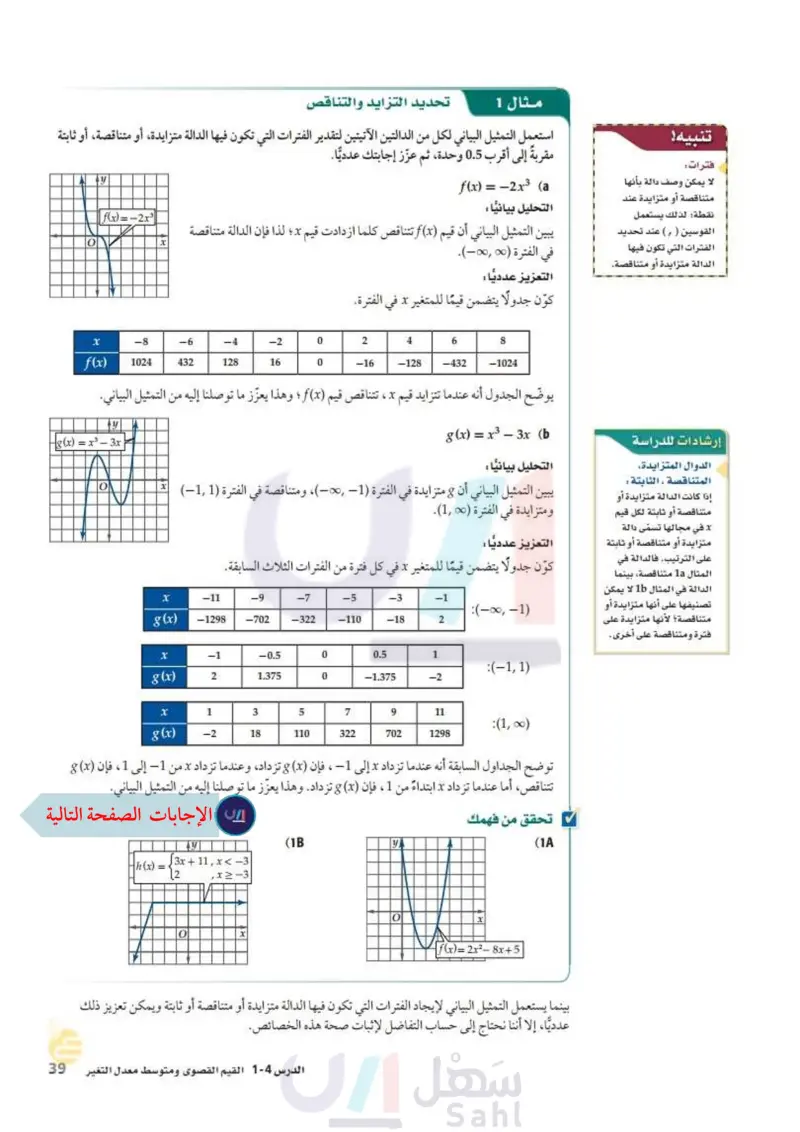
استعمل التمثيل البياني لدالة لأحدد الفترات التي تكون فيها الدالة: متزايدة، ثابتة، متناقصة، وأحدد القيم العظمي والصغرى لها.

1A- استعمل التمثيل البياني لكل من الدالتين الآتيتين، لتقدير الفترات التي تكون فيها الدالة متزايدة أو متناقصة أو ثابتة .


فترات
إذا كانت الدالة متزايدة أو متناقصة أو ثابته لكل قيم x في مجالها تسمى متزايدة، متناقصة ، ثابتة على الترتيب .

القيم القصوى
قيمة قصوى محلية

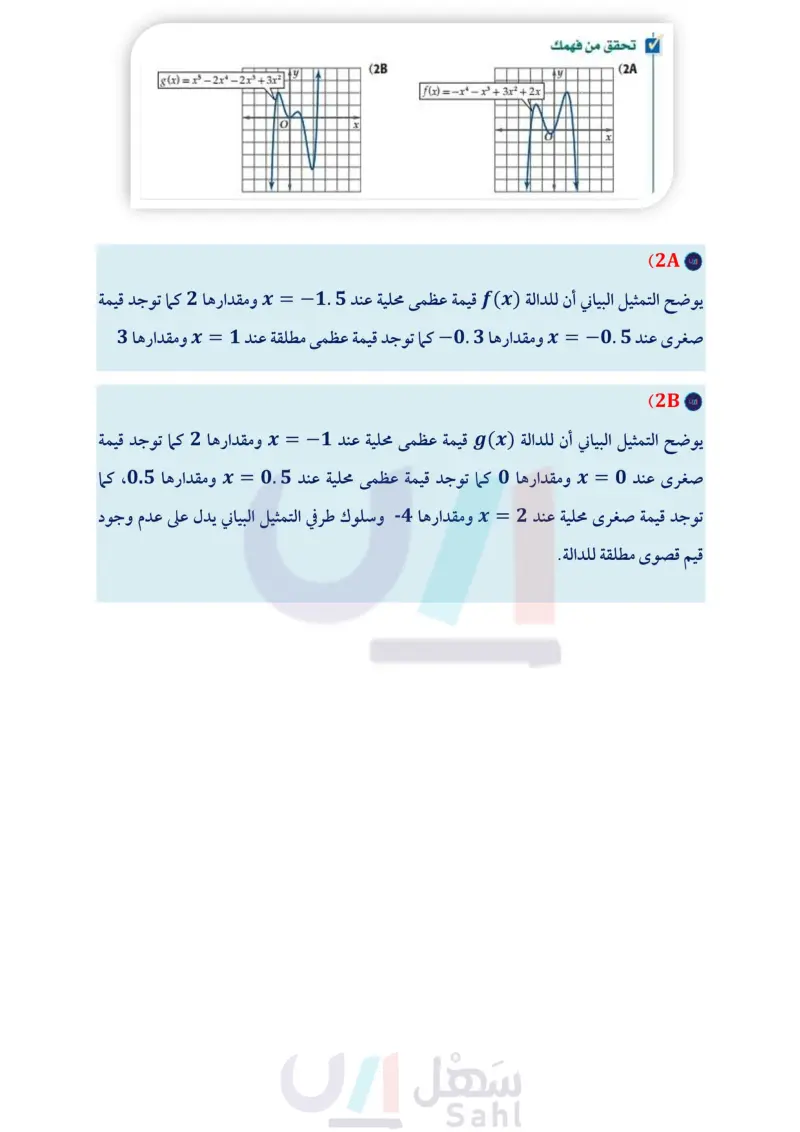
2A- استعمل التمثيل البياني لتقدير قيم x التي يكون للدالة f(x0 عندها قيم قصوى مقربة إلى أقرب 0.5 وحدة. وأوجد قيم الدالة عندها


ضبط

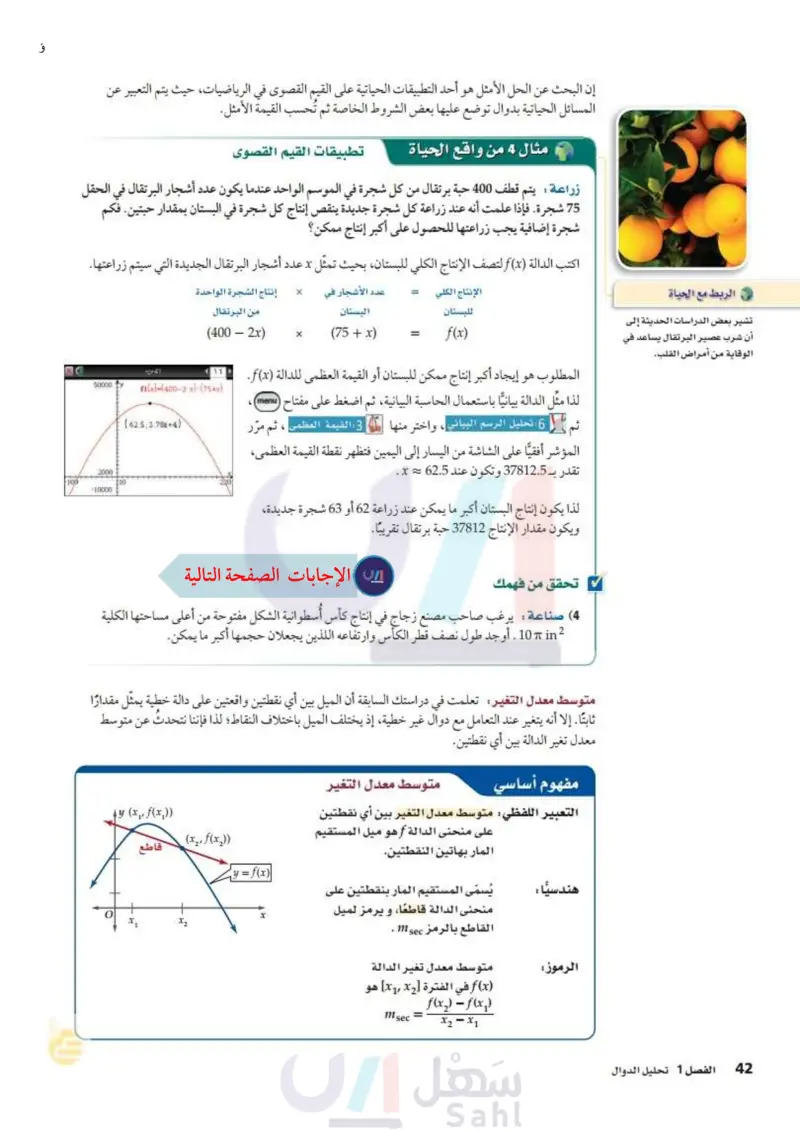
تشير بعض الدراسات الحديثة إلى أن شرب عصير البرتقال يساعد في الوقاية من أمراض القلب.

السرعه المتوسطة
إن الاجسام الساقطة تصل أخيرا إلى سرعة ثابتة تسمى السرعة الحدية.
الشكل 1.4.1

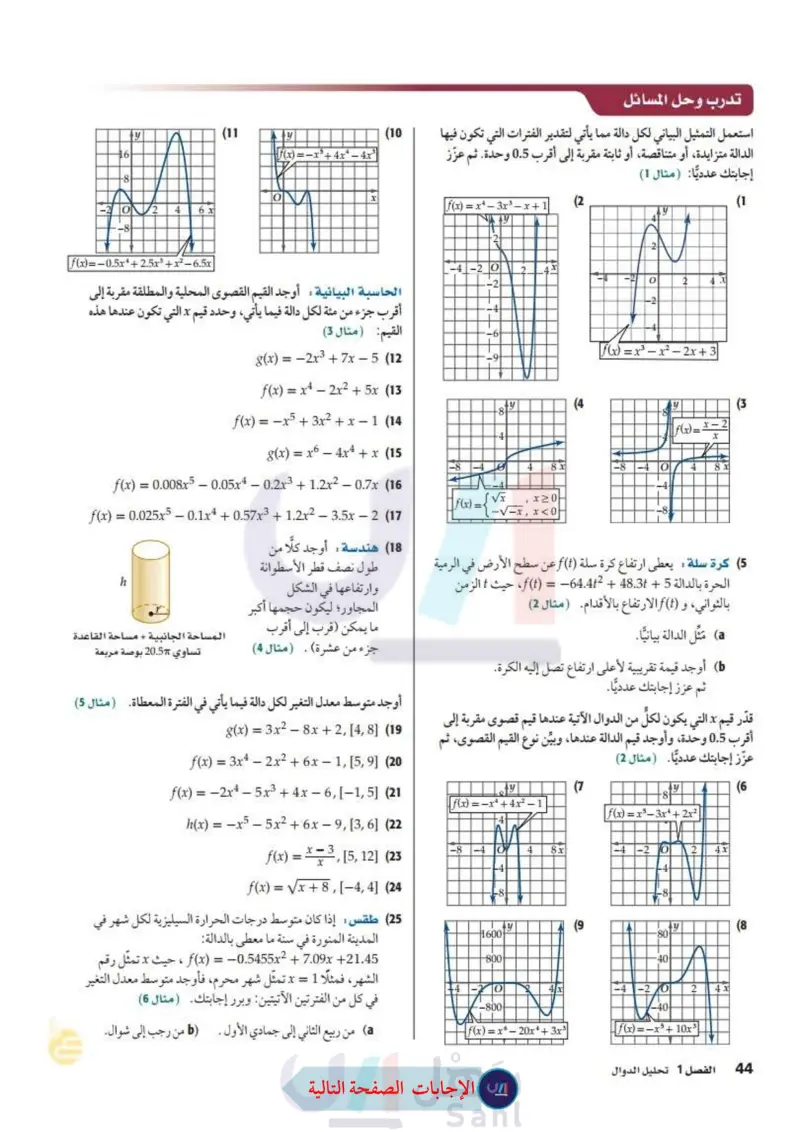
1- استعمل التمثيل البياني لكل مما يأتي لتقدير الفترات التي تكون فيها الدالة متزايدة او متناقصة أو ثابتة مقربة إلى أقرب 0.5 وحدة ثم عزز إجابتك عدديا:


6- قدر قيم x التي تكون لكل من الدوال الاتية قيم قصوى مقربة إلى أقرب 0.5 وحدة. وأوجد قيم الدالة عندها، وبين نوع القيم القصوى ثم عزز إجابتك عدديا:


10- قدر قيم x التي تكون لكل من الدوال الاتية قيم قصوى مقربة إلى أقرب 0.5 وحدة. وأوجد قيم الدالة عندها، وبين نوع القيم القصوى ثم عزز إجابتك عدديا:





استعمل التمثيل البياني للدالة في السؤال 18 اعلاه، وقدر قيمة x التي يكون للدالة ندها قيمة قصوى مقربة إلى أقرب 0.5 وحدة.