تشابه المثلثات - رياضيات 1 - أول ثانوي
الوحدة الأولى: الجبر والعلاقات والدوال
الوحدة الثانية: التشابه
الوحدة الثالثة: نظريات التناسب في المثلث

فكر وناقش
عمل تعاوني

مسلمة
حاول أن تحل1: بين أيا من أزواج المثلثات التالي تكون متشابهة. اكتب المثلثات المتشابهة بترتيب الرؤوس المتناظرة.

مثال حاول أن تحل2: في المثلث أ ب ج، د ينتمي الى أ ج حيث د هـ يوازي ب ج، ب د= 1,2 سم، أ هـ = 3 سم ، أ ج = 4 سم ، د هـ 4,2 سم.
نتيجة1

تابع نتيجة1
مثال حاول أن تحل3: في الشكل المقابل أ ب ج مثلث، د ينتمي الى أ ب، رسم د هـ يوازي ب ج ويقطع أ ج في هـ، د و يوازي أ ج ويقطع ب ج في و. برهن أن: مثلث أ د هـ يشابه مثلث د ب و
نتيجة2
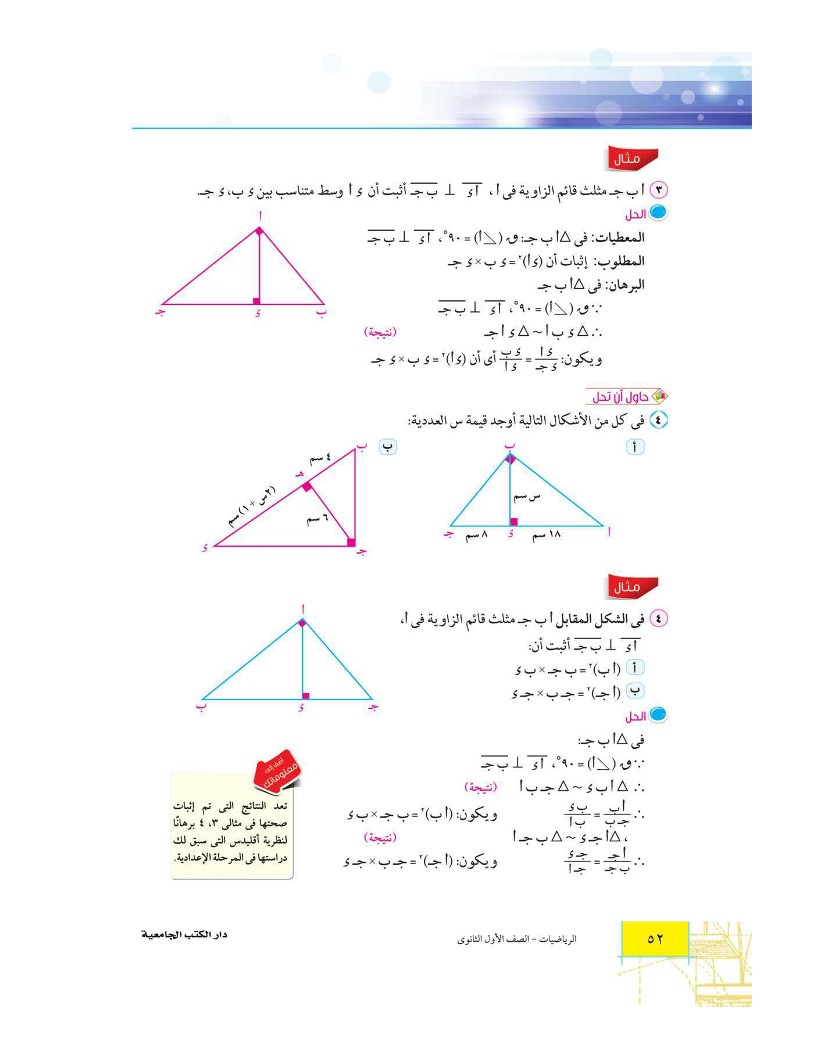
مثال حاول أن تحل 4 أ ب ج مثلث قائم الزاوية في أ، أ د عمودي على ب ج أثبت أن د أ وسط متناسب بين د ب، د ج
مثال4: في الشكل المقابل أ ب ج مثلث قائم الزاوية في أ، أ د عمودي على ب ج أثبت أن:

حاول أن تحل5: أوجد قيمة س، ص العددية في أبسط صورة (الأبعاد مقدرة بالسنتيمترات)
القياس غير المباشر مثال5

حاول أن تحل 6: أوجد المسافة س في كل من الحالات الآتية:
نظرية1

مثال حاول أن تحل7: في الشكل المقابل: ب، ص، ج على استقامة واحدة. أثبت أن:

نظرية2
مثال8: أ ب ج مثلث، أ ب = 8سم، أ ج = 10سم، ب ج = 12سم ، هـ ينتمي الى أ ب حيث أ هـ = 2سم، د ينتمي الى ب ج حيث ب د = 4سم

تابع مثال 8
حاول أن تحل8: في كل من الأشكال التالية أوجد قيمة الرمز المستخدم في القياس مفسراً إجابتك
مثال حاول أن تحل9 تحقق من فهمك: أ ب ج مثلث، د ينتمي الى ب ج حيث ( أ ج )² = ج د × ج ب أثبت أن: المثلث أ ج د يشابه المثلث ب ج أ

أذكر أي الحالات يكون فيها المثلثان متشابهين، وفي حالة التشابه اذكر سبب التشابه
أوج قيمة الرمز المستخدم في القياس:
في الشكل المقابل: أ ب ج مثلث قائم الزاوية أ د عمودي على ب ج
أ ب ، د ج وتران في دائرة، أ ب تقاطع د ج يساوي (هـ) حيث هـ خارج الدائرة، أ ب = 4سم، د ج = 7سم، ب هـ = 6سم. أثبت أن المثلث أ د هـ يشابه المثلث ج ب هـ، ثم أوجد طول جـ هـ
أ ب ج، د هـ و مثلثان متشابهان. رسم أ س عمودي على ب ج ليقطعه في س، ورسم د ص عمودي على هـ و ليقطعه في س. أثبت أن ب س
في المثلث أ ب ج، أ ج اكبر من أ ب، م ينتمي الى أ ج حيث ق(الزاوية أ ب م) = ق (الزاوية ج) أثبت أن (أ ب)²= أ م × أ ج.

في الشكل المقابل: أ ب ج مثلث قائم الزاوية في أ، أ د عمودي على ب ج ، د هـ عمودي على أ ب ، د و عمودي على أ ج أثبت أن:
أ ب ج مثلث قائم الزاوية في أ، رسم أ د عمودي على ب ج ليقطعه في د. إذا كان ب د/ د ج = 1/ 2، أ د = 6 جذر 2سم أوجد طول كل من ب د ، أ ب، أ ج.
في الشكل المقابل: أ ب ج مثلث منفرج الزاوية في أ، أ ب = أ ج رسم أ د عمودي على أ ب ويقطع بج في د. أثبت أن: 2( أ ب )² = ب د × ب ج
تعبر المجموعتان أ، ب عن أطوال أضلاع مثلثات مختلفة بالسنتمترات. اكتب أمام كل مثلث من المجموعة أ رمز المثلث الذي يشابهه من المجموعة ب
في الشكل المقابل: أ ب ج مثلث فيه أ ب = 6سم ، ب ج = 9سم، أ ج = 7،5سم، د نقطة خارجة عن المثلث أ ب ج حيث د ب = 4سم ، د أ = 5 سم. أثبت أن:
من الشكل المقابل أكمل:

في الشكل المقابل: أ ب ج يشابه س ص ع، هـ منتصف ب ج، م منتصف ص ع ، جد عمودي على أ ب، ع ل عمودي على س ص أثبت أن:
أ ب ج ، س ص ع مثلثان متشابهان، حيث أ ب اكبر من أ ج، س ص اكبر من س ع. هـ ، ل منتصفي ب ج ، ص ع على الترتيب، رسم أ و عمودي على ب ج ، س م عمودي على ص ع أثبت أن مثلث أ هـ و يشابه المثلث س ل م
أ ب ج مثلث، د ينتمي الى ب ج حيث (أ د)² = ب د × د ج ، ب أ × أ د = ب د × أ ج أثبت أن:
يبين المخطط المقابل موقع محطة خدمة وتموين سيارات يراد إقامتها على الطريق السريع عند تقاطع طريق جانبي يؤدي إلى المدينة ج و عمودياً على الطريق السريع بين المدينتين أ، ب.
استخدم برنامج خرائط قوقل ارث لحساب أقصر بعد بين عواصم محافظات جمهورية مصر العربية






