المسلمات والبراهين الحرة - الرياضيات 1-1 - أول ثانوي

المسلمات والبراهين الحرة Postulates and Paragraph Proofs 1-5 رابط الدر www.ien.edu.sa فيما سبق الماذا؟ درست استعمال التبرير التجربة في الصورة المجاورة تُظهر سقوط الريشة والتفاحة بالسرعة نفسها في الاستنتاجي بتطبيق قانون حجرة مفرغة من الهواء، وتوضح هذه التجربة قوانين نيوتن في الجاذبية الأرضية الفصل المنطقي وقانون والقصور الذاتي، والتي تُقبل على أنها حقائق أساسية في الفيزياء. وفي الهندسة أيضًا توجد قوانين تقبل على أنها صحيحة دون برهان. القياس المنطقي. ( الدرس 4-1) والآن: أتعرف المسلّمات الأساسية حول النقاط والمستقيمات والمستويات وأستعملها. أكتب برهانا حرا. المفردات: المسلمة axiom or postulate البرهان proof النظرية theorem البرهان الحر paragraph proof قراءة الرياضيات النقاط والمستقيمات والمستويات المسلمة أو البدهية عبارة تعطي وصفًا لعلاقة أساسية بين المفاهيم الهندسية الأولية وتُقبل على أنها صحيحة دون برهان درست مبادئ أساسية حول النقاط والمستقيمات والمستويات، ويمكن اعتبار هذه المبادئ الأساسية مسلّمات. مسلمات التعبير اللفظي 1.1 أي نقطتين يمر بهما مستقيم واحد فقط. 1.2 أي ثلاث نقاط لا تقع على استقامة واحدة يمر بها مستوى واحد فقط. 1.3 كل مستقيم يحوي نقطتين على الأقل. 1.4 كل مستوى يحوي ثلاث نقاط على الأقل ليست على استقامة واحدة. 1.5 إذا وقعت نقطتان في مستوى، فإن المستقيم الوحيد المار بهما يقع كليًّا في ذلك المستوى. النقاط والمستقيمات والمستويات مثال n K R P B A C R P n B K L C E B K A m .R, أضف إلى مطويتك المستقيم n هو المستقيم الوحيد المار بالنقطتين P و R . المستوى X هو المستوى الوحيد الذي يحوي النقاط A و B و C ، والتي لا تقع على استقامة واحدة. المستقيم n يحوي النقاط P و Q يحوي المستوى النقاط L و B و و C و E ، وهي ليست على استقامة واحدة. النقطتان A و B في المستوى ، ويمر بهما المستقيم m ؛ إذن المستقيم m يقع كليا في المستوى و .K يرمز للمستقيم بحرف تتعلق المسلّمات الآتية بتقاطع المستقيمات والمستويات. صغير مائل مثل: ...,,, أو بأي نقطتين واقعتين عليه مثل : .. ,AB, AC يرمز للمستوى بحرف كبير مائل مثل: ... , أو بأي ثلاث نقاط فيه ليست على استقامة واحدة XYZ مسلمتان التعبير اللفظي تقاطع المستقيمات والمستويات 1.6 إذا تقاطع مستقيمان، فإنهما يتقاطعان في نقطة واحدة فقط. 1.7 إذا تقاطع مستويان، فإن تقاطعهما يكون مستقيما. S P G لله F مثال أضف إلى مطويتك المستقيمان ، و t يتقاطعان في النقطة P يتقاطع المستويان 7 و 6 في المستقيم الدرس 5-1 - المسلمات والبراهين الحرة التP45 Ministry of Education 2024-1446

Q m E G B تعد المسلّمات أساسًا للبراهين والتبريرات المتعلقة بالنقاط والمستقيمات والمستويات. مثال 1 من واقع الحياة تحديد المسلمات هندسة معمارية : اذكر المسلّمة التي تبرر صحة كل عبارة مما يأتي: a) يحتوي المستقيم m على النقطتين F و G، ويمكن أن تقع النقطة E أيضًا على المستقيم m. المسلمة ،1.3 التي تنص على أن كل مستقيم يحوي نقطتين على الأقل. حيث إن حافة البناية عبارة عن المستقيم .m. والنقاط G,, واقعة على هذه الحافة؛ لذا فهي تقع على المستقيم m. يتقاطع المستقيمان s و t في النقطة D. المسلّمة 1.6 التي تنص على أنه إذا تقاطع مستقيمان فإنهما يتقاطعان في نقطة واحدة فقط. حيث إن الشبكة المثلثة أعلى واجهة البناية تتشكل من مستقيمات متقاطعة، والمستقيمان ، و t يتقاطعان في نقطة واحدة فقط د هي D تحقق من فهمك إرشادات للدراسة نظام المسلمات هو مجموعة من المسلمات التي يمكن استعمال بعضها أو كلها لاستنتاج النظريات عن طريق المنطق. A النقاط تحدد مستوى. (18) يتقاطع المستويان P و Q في المستقيم m. يمكنك استعمال المسلّمات لتفسير تبريرك في أثناء تحليل بعض العبارات. مثال 2 تحليل العبارات باستعمال المسلمات حدد ما إذا كانت كل جملة مما يلي صائبة دائمًا أو صائبة أحيانًا أو غير صائبة أبدًا. فسّر تبريرك. a إذا تقاطع مستقيمان واقعان في مستوى واحد، فإن نقطة تقاطعهما تقع أيضًا في المستوى الذي يحويهما. صائبة دائمًا؛ تنص المسلّمة 1.5 على أنه إذا وقعت نقطتان في مستوى، فإن المستقيم الوحيد المار بهما يقع بكامله في ذلك المستوى، وبما أن المستقيمين يقعان في المستوى نفسه، فإن أي نقطة واقعة عليهما بما فيها نقطة التقاطع تقع في المستوى نفسه. أي أربع نقاط لا تقع على استقامة واحدة. صائبة أحيانًا: تنص المسلّمة 1.3 على أن كل مستقيم يحوي نقطتين على الأقل، وهذا يعني أنه يمكن أن يحوي المستقيم نقطتين أو أكثر؛ إذن يمكن أن تكون أربع نقاط ليست على استقامة واحدة مثل في الشكل المجاور، أو تكون على استقامة واحدة مثل A, B, C, D . تحقق من فهمك E B C D (2) المستقيمان المتقاطعان يحددان مستوى. 2B تتقاطع ثلاثة مستقيمات في نقطتين. A البرهان الحر عند إثباتك نتيجة تخمين ما ، فإنك تستعمل التبرير الاستنتاجي للانتقال من الفرض إلى النتيجة التي تريد إثبات صحتها بكتابة برهان ، وهو دليل منطقي فيه كل عبارة تكتبها تكون مبررة بعبارة سبق إثباتها أو قبول صحتها. وزارة التعليم Ministry of Education 2024-1446 الفصل 1 التبرير والبرهان 46

في حال إثبات صحة عبارة (أو تخمين) فإنها تُسمى نظرية، ويمكن بعد ذلك استعمالها في البراهين لتبرير صحة عبارات أخرى . مفهوم أساسي خطوات كتابة البرهان الخطوة 1 اكتب المعطيات، وارسم شكلا يوضحها إن أمكن. الخطوة 2 اكتب العبارة أو التخمين المطلوب إثباته. الخطوة 3: استعمل التبرير الاستنتاجي لتكوين سلسلة منطقية من العبارات التي تربط المعطيات بالمطلوب. الخطوة :4: برّر كل عبارة مستعملا تعريفات أو خصائص جبرية أو مسلمات أو نظريات. الخطوة 5 اكتب العبارة أو التخمين الذي قمت بإثباته. أضف إلى مطويتك المعطيات (الفرض) العبارات والمبررات المطلوب (النتيجة) البرهان الحر هو أحد أنواع البراهين، وفيه تُكتب فقرة تفسر أسباب صحة التخمين في موقف مُعطّى. مثال 3 كتابة البرهان الحر 6 المعطيات M نقطة منتصف XY ، اكتب برهانًا حرًا لإثبات أن XM = MY الخطوتان 1 و 2 المعطيات M نقطة منتصف XY المطلوب : Y XM = MY X M إرشادات حل المسألة العمل عكسيا إحدى استراتيجيات الخطوتان 3 و 4 6 إذا كانت M نقطة منتصف XY ، فإنه بحسب تعريف نقطة منتصف القطعة المستقيمة تكون XM و MY لهما الطول نفسه. ومن تعريف التطابق، إذا كانت القطعتان المستقيمتان لهما الطول نفسه، فإنهما تكونان متطابقتين. كتابة البرهان هي العمل عكسيًا، وذلك بأن تبدأ من المطلوب وتعمل عكسيا خطوة بخطوة حتى تصل الخطوة 5 لذا XM = MY إلى المعطيات. تحقق من فهمك C إذا علمت أن تقع على AB، حيث AC = CB ، فاكتب برهانا حرًا لإثبات أن C هي نقطة منتصف AB . يعرف التخمين في مثال 3 بنظرية نقطة المنتصف. نظرية 1.1 نظرية نقطة المنتصف إذا كانت M نقطة منتصف AB ، فإن AM = MB A M B أضف إلى مطويتك الدرس 5-1 - المسلمات والبراهين الحرة التP47 Ministry of Education 2024-1446

المثال 1 اذكر المسلّمة التي تبرر صحة كل عبارة من العبارات الآتية: (1) المستويان P و Q يتقاطعان في المستقيم . (2) المستقيمان T و n يتقاطعان في النقطة D. (3) المستقيم n يحوي النقاط C,D,E. (4) المستوى P يحوي النقاط . (5) المستقيم n يقع في المستوى .Q (6) المستقيم r هو المستقيم الوحيد الذي يمر بالنقطتين A و D . m A Q F P n D C E المثال 2 حدد ما إذا كانت كل جملة مما يلي صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. وفسّر تبريرك. (7) تتقاطع ثلاثة مستويات في مستقيم. ( المستقيم r يحوي النقطة P فقط. (9) يمر مستقيم واحد فقط بنقطتين معلومتين. في الشكل المجاور: يقع AK في المستوى P وتقع النقطة M على NE اذكر المسلمة التي تثبت صحة كل من العبارات الآتية: 10 K, N, تقع في مستوى واحد. 11) NE يحوي النقطتين M، N. 12 النقاط A,, تقع في المستوى نفسه. المثال 3 (13) برهان في الشكل المجاور AE = DB، والنقطة C نقطة منتصف كلّ من AE و DB . اكتب برهانًا حرًا لإثبات أن AC = CB . . B P M N A K C E A D E B n h C 00000000 D H K e m وزارة التعليم Ministry of Education 2024-1446 E Q g تأكد تدرب وحل المسائل المثال 1 كعك : اذكر المسلّمة التي تبرر صحة كل عبارة من العبارات الآتية: (14) المستقيمان n و يتقاطعان في النقطة K. (15) المستويان , يتقاطعان في المستقيم m. (16) النقاط , تحدد مستوى. D, K, H 17) النقطة D تقع على المستقيم 1 المار بالنقطتين . 18 النقاط تقع في المستوى نفسه. ,,,,, 19 EF يقع في المستوى.Q. 20 المستقيمان يتقاطعان في النقطة ) . g , 48 الفصل 1 التبرير والبرهان

المثال 2 حدد ما إذا كانت كل جملة مما يلي صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. فسّر تبريرك. 21) يوجد مستوى واحد فقط يحوي النقاط الثلاث التي لا تقع على استقامة واحدة. (22) ثلاثة مستقيمات على الأقل تمر بالنقطتين J و K. ,,, (23) إذا وقعت النقاط في المستوى ، فإنها تقع على استقامة واحدة. (24) تقع النقطتان X و Y في المستوى .. وأي نقطة على استقامة واحدة مع X و Y تقع أيضًا في المستوى Z. , (25) النقاط A تحدد مستوى المثال 3 (26) برهان : إذا علمت أن Y هي نقطة منتصف XZ ، وأن Z هي نقطة منتصف XZ ، وأن Z هي نقطة منتصف YW ، فأثبت أن XY = ZW هي . (27) برهان النقطة L فأثبت أن LK = MK نقطة منتصف JK ، ويتقاطع JK مع MK في النقطة K . إذا كان MK = JL ، (28 خرائط أمام خالد طريقان للانتقال من الموقع A إلى الموقع B كما يظهر في الخريطة المجاورة. إذا كان الحد الأعلى للسرعة المسموح بها على الطريق (1) هو 90km/h، وعلى الطريق (2) هو 110km/h a أي الطريقين يبدو أقصر طولا؟ فسّر تبريرك. ( إذا كانت المسافة من A إلى B عبر الطريق (1) تساوي 16.8km ، والمسافة بينهما عبر الطريق (2) تساوي 17.6km، فأي الطريقين أسرع وصولًا، إذا قاد خالد سيارته بالحد الأعلى للسرعة المسموح بها؟ في الشكل المجاور، CD و CE واقعان في المستوى P، DH و D واقعان في المستوى Q. اذكر المسلمة التي يمكن استعمالها لإثبات صحة كل عبارة فيما يأتي : (29) النقطتان C و B على استقامة واحدة. → EG (30 يحوي النقاط E, F, G 31) النقطتان D و F تقعان على استقامة واحدة. (32) النقاط C, D, B تقع في المستوى نفسه. J C, H, D, (33) المستوى Q يحوي النقاط . 34) المستوى P يتقاطع مع المستوى.Q في CD. النقطة A الطريق (2) النقطة B Q الطريق (1) E H A F D G B J الدرس 5-1 - المسلمات والبراهين الحرة الت49م Ministry of Education 2024-1446

الربط مع الحياة تُصمَّم أسطح المنازل بطرائق هندسية مختلفة لمنع تسرب الماء. من هذه الطرائق استعمال مواد عازلة لا تسمح بنفاذ الماء، أو أن تُبنى مائلة؛ لتسهيل (35) هندسة عمارة: يُحسب ميل السطح عادة بقسمة الارتفاع مقيسًا بالبوصة على المسافة الأفقية مقيسة بالقدم. استعمل العبارات أدناه لتكتب برهانًا حرًا للعبارة الآتية : ميل السطح في تصميم أحمد غير كاف. عند استعمال مواد عازلة للماء، يجب أن يكون الميل 7 بوصة لكل قدم على الأقل. 4 حتى ينحدر الماء بتأثير الجاذبية الأرضية، يجب أن يكون ميل السطح 4 بوصات لكل قدم. صمم أحمد سطح منزله بحيث يكون مائلا. الميل في تصميم أحمد يساوي 2 بوصة لكل قدم. انحدار الماء عنها بتأثير (36) رياضة : أُقيمت بطولة شاركت فيها ثماني فرق كرن الجاذبية الأرضية. قدم للناشئين. ما عدد المباريات التي ستجرى في الدور الأول؟ ارسم شكلا يوضح عدد مباريات الدور الأول. أي مسلّمة يمكنك استعمالها لتبرير هذا الشكل؟ أوجد طريقة حسابية لإيجاد عدد المباريات التي ستجرى الدور الأول، بغض النظر عن عدد الفرق المشاركة في البطولة؟ مسائل مهارات التفكير العليا ستجرى مباريات الدور الأول بين الفرق الثمانية خلال شهر شوال (37) مسألة مفتوحة ارسم شكلا يحقق خمسًا من المسلمات السبع التي تعلمتها في هذا الدرس. اشرح كيف تحققت كل منها في الشكل. 38 اكتشف الخطأ قام كل من عمر وسعيد بكتابة برهان لإثبات أنه إذا كانت AB تطابق BD ، وكانت على استقامة واحدة، فإن B نقطة منتصف AD. وقد بدأ كل منهما برهانه بطريقة مختلفة. أيهما بدأ برهانه بطريقة صحيحة ؟ فسر إجابتك. , 50 الفصل 1 التبرير والبرهان إذا كانت B نقطة منتصف AB ، فإن B تقسم AD إلى قطعتين مستقيمتين متطابقتين. سعيد AB تطابق BD ، والنقاط A,B,C تقع على استقامة واحدة. تبرير حدد ما إذا كانت الجملة الآتية صحيحة أحيانًا أو صحيحة دائمًا أو غير صحيحة أبدًا. فسّر تبريرك أو أعط مثالا مضادا: (39) أيُّ ثلاث نقاط يمر بها مستوى واحد فقط. (40) اكتب بين أوجه الشبه والاختلاف بين المسلمات والنظريات. وزارة التعليم Ministry of Education 2024-1446

تدريب على اختبار (41 أيُّ العبارات الآتية ليست صائبة؟ B C D أي ثلاث نقاط ليست على استقامة واحدة تحدد مستوى واحدًا فقط . يتقاطع المستقيمان في نقطة واحدة فقط. يوجد على الأقل مستقيمان يحويان النقطتين نفسيهما. تقسم نقطة المنتصف القطعة المستقيمة إلى قطعتين متطابقتين. (42) ما أكبر عدد من المناطق التي تتشكل عندما تقطع ثلاثة مستقيمات مختلفة دائرة ؟ 6 C 4 A 7 D 5 B مراجعة تراكمية استعمل قانون الفصل المنطقي أو قانون القياس المنطقي؛ لتحصل على نتيجة صائبة من العبارات الآتية إن أمكن، واذكر القانون الذي استعملته. وإذا تعذر الحصول على نتيجة صائبة، فاكتب " لا نتيجة صائبة". فسر تبريرك (الدرس 4-1) (43) (1) إذا كانت الزاويتان متقابلتين بالرأس، فإنهما لا تكونان متجاورتين على مستقيم. (2) إذا كانت الزاويتان متجاورتين على مستقيم فهما غير متطابقتين. 44) (1) إذا كانت الزاوية حادة، فإن قياسها أقل من 90 (2) EFG حادة. اكتب العبارتين الشرطيتين الآتيتين على صورة إذا) ... فإن ... ) . (الدرس (3-1) (45) يُكتب اسم الطالب المتفوق في لوحة الشرف. و استعد للدرس اللاحق حُلَّ كلًّا من المعادلات الآتية: 4x - 3 = 19 47 (46) يخشى البطل أن يخسر. 5(x2+2)=30 (49 } 3 x + 6 x + 6 = 14 (48) الدرس 5-1 - المسلمات والبراهين الحرة الت51م Ministry of Education 2024-1446

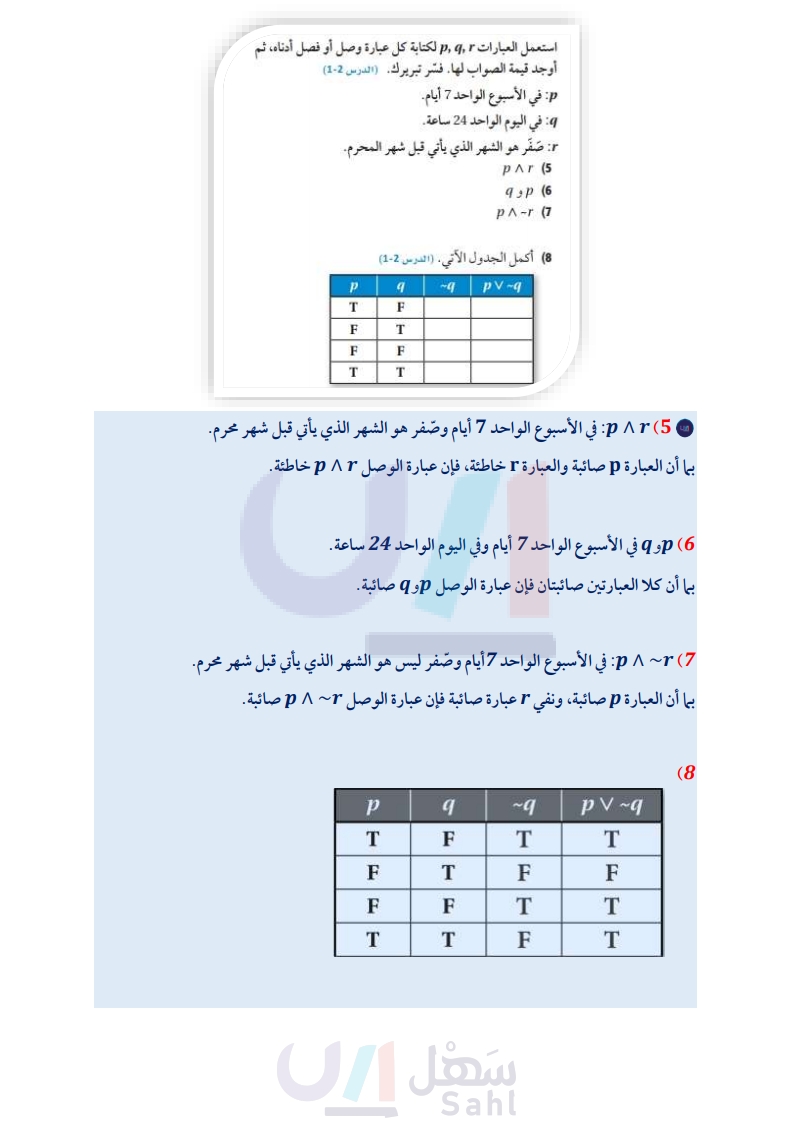
الفصل 1 اختبار منتصف الفصل الدروس 1-1 إلى 15 اكتب تخمينًا يصف النمط في كل متتابعة مما يأتي، ثم استعمله لإيجاد استعمل أشكال فن أدناه لتحديد قيمة الصواب لكلِّ من العبارات الحد التالي في كل منها . الدرس (1-1) الشرطية الآتية وفسر تبريرك . (الدرس (3-1) (2 5, 5, 10, 15, 25, ...... (1 المستطيلات المربعات التعامد أعط مثالا مضادا يبين أن كلا من التخمينين الآتيين خاطئ الدرس (1-1) = إذا كان ABB ، فإن B نقطة منتصف AC . (4 إذا كان n عددًا حقيقيا، فإن n <3 التوازي (14) إذا كان المضلع مربعًا ، فإنه يكون مستطيلاً. (15) إذا كان المستقيمان متعامدين، فإنهما لا يمكن أن يكونا متوازيين. استعمل العبارات لكتابة كل عبارة وصل أو فصل أدناه، ثم (16) كرة قدم : تقابل فريقا الفرسان والفهود في المباراة النهائية. أوجد قيمة الصواب لها فسّر تبريرك (الدرس (2-1) • p في الأسبوع الواحد 7 أيام. في اليوم الواحد 24 ساعة. :r: صَفَر هو الشهر الذي يأتي قبل شهر المحرم. pr (5 6) p و 9 P^~r (7 (8) أكمل الجدول الآتي. (الدرس (2-1) p 9 ~9 pv ~q T F F T F F T T حدد الفرض والنتيجة في كلّ من العبارات الشرطية الآتية: (الدرس (3-1) (9) إذا كان للمضلع خمسة أضلاع، فإنه خماسي. 10) إذا كان 10 = 6 - 4x ، فإن 4 = x. (11) الزاوية التي قياسها أقل من 900 تكون حادة. حدد قيمة الصواب لكلِّ من العبارتين الشرطيتين الآتيتين. وإذا كانت العبارة صائبة، فبرر إجابتك (الدرس (3-1) a معتمدًا على المعطيات، حدد ما إذا كانت النتيجة صائبة أم لا في كل مما يأتي. وفسّر تبريرك (الدرس 4-1) المعطيات الفريق الفائز بالكأس هو الفريق الذي يحرز أهدافًا أكثر في نهاية المباراة. أحرز فريق الفرسان 3 أهداف، بينما أحرز فريق الفهود هدفين. النتيجة فاز فريق الفرسان بالكأس. (17) اختيار من متعدد أي العبارات الآتية تنتج منطقياً عن العبارتين (1) و (2)؟ (الدرس 4-1) (1) إذا كنت أحد طلاب المرحلة الثانوية، فإن عمرك 16 سنة على الأقل. (2) إذا كان عمرك 16 سنة على الأقل، فإن عمرك يؤهلك لقيادة السيارة. A إذا كان عمرك يؤهلك لقيادة السيارة، فإنك أحد طلاب المرحلة الثانوية. إذا كان عمرك لا يؤهلك لقيادة السيارة، فأنت في المرحلة المتوسطة. C إذا كنت أحد طلاب المرحلة الثانوية، فإن عمرك يؤهلك لقيادة السيارة . D إذا كان عمرك 16 سنة على الأقل، فإنك أحد طلاب المرحلة الثانوية. حدد ما إذا كانت كل جملة مما يأتي صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. وفسر تبريرك (الدرس 5-1) 18 النقاط ليست على استقامة واحدة، وتقع جميعها في 12) 21 و 22 متكاملتان. 13) 1 و 4 متطابقتان. 52 الفصل 1 التبرير والبرهان 1 2 6 4 3 المستوى M. 19) يوجد مستقيم واحد فقط يمر بالنقطتين . , (20) المستقيم a يحتوي على النقطة ) فقط . وزارة التعليم Ministry of Education 2024-1446