المشتقات - رياضيات3-3 - ثالث ثانوي
الفصل السادس: الإحداثيات القطبية والأعداد المركبة
الفصل السابع: الاحتمال والإحصاء
الفصل الثامن: النهايات والاشتقاق
نشاط الفصل السادس: الإحداثيات القطبية والأعداد المركبة
نشاط الفصل السابع: الاحتمال والإحصاء
نشاط الفصل الثامن: النهايات والاشتقاق
المشتقات Derivatives 8-4 فيما سبق. لماذا ؟ درست حساب ميل المماسات ركل أحمد كرة رأسيا إلى أعلى من ارتفاع ، فانطلقت بسر لإيجاد معدل التغير اللحظي (الدرس (3-8) والان سرعة 65ft/s يمكنك استعمال معادلات الحركة بتسارع ثابت التي درستها في الفيزياء لكتابة دالة تصف ارتفاع الكرة بعد 1 ثانية، ومن ثم تحديد ما إذا كانت الكرة ستبلغ ارتفاع ft 68 أم لا. أجد ميل منحنى دالة غير خطية باستعمال المشتقات. قواعد أساسية للاشتقاق: استعملت النهايات في الدرس 3-8 لتحديد ميل . أستعمل قواعد الاشتقاق مماس منحنى الدالة (f(x عند أي نقطة عليه ، وتُسمى هذه النهاية مشتقة الدالة ويرمز لها بالرمز (x) ، وتُعطى بالصيغة لإيجاد المشتقات. المفردات المشتقة f'(x) = lim f(x + h) -f(x) h→0 h derivative الاشتقاق differentiation المعادلة التفاضلية differential equation المؤثر التفاضلي differential operator قراءة الرياضيات . المشتقات يقرأ الرمز (f(x مشتقة f بالنسبة للمتغير x ، أو f prime of x. رابط الدرس www.icn.edu.sa بشرط وجود هذه النهاية، وتُسمى عملية إيجاد المشتقة الاشتقاق، وتُسمّى النتيجة معادلة تفاضلية. مثال 1 مشتقة دالة عند أي نقطة أوجد مشتقة 8 + f(x) = 4x2 - 5x باستعمال النهايات، ثم احسب قيمة المشتقة عندما 15 = x . صيغة المشتقة f'(x) = lim 0-4 f(x + h) - f(x) h f(x + h)=4(x+h)² - 5(x + h) +8, = lim f(x)=4x²-5x+8 h-0 4(x+ h)-5(x+h) +8 (4x²-5x+8) h 8xh+4h²-5h بسط = lim = : lim اقسم على h-0 h-0 h(8x + 4h - 5) h = lim (8x+4h - 5) h→0 = [8x+4(0)5] = 8x-5 h تاريخ الرياضيات شرف الدين الطوسي العالم المسلم شرف الدين الطوسي (المتوفى عام (610هـ) من خلال دراسته المعادلات التي درجتها 35 استعمل في حل هذه المعادلات القيمة العظمى للعبارات الجبرية أي أن مشتقة (f(x هي 5 - f(x) = 8x . احسب (f(x عندما 1,5 = x . f'(x)=8x-5 المعادلة الأصلية f'(x)=8x-5 f '(1) = 8(1) - 5 f'(1)=3 x = 1, x=5 f'(5)=8(5)-5 f'(5) = 35 وأخذ" المشتق الأول لهذه العبارات تحقق من فهمك من دون أن يستعمل اسمه (المشتق بسط الأول)، وبرهن على أن جذر المعادلة أوجد مشتقة (f(x باستعمال النهايات، ثم احسب قيمة المشتقة عند قيم x المعطاة: التي يحصل عليها إذا ما عُوض به في العبارة الجبرية، أعطى القيمة العظمى للعبارة. 114 f(x)=6x²+7, x = 2,5 (1A يرمز مشتقة الدالة. لمشتقة (y = f(x أيضًا بالرموز . الفصل 8 النهايات والاشتقاق df dx dy dx f(x)=-5x²+2x-12, x = 1,4 (1B .... d ل ، وإذا سبق الدالة المؤثر التفاضلي ل ، فإن ذلك يعني إيجاد وزارة التعليم Ministry of Education 2024-1446

تاريخ الرياضيات: شرف الدين الطوسي
أهداف درس المشتقات
حتى هذه اللحظة استعملت النهاية؛ لإيجاد كل من المشتقة وميل المماس والسرعة المتجهة اللحظية. وتعد قاعدة مشتقة القوة من أكثر القواعد فعالية لإيجاد المشتقات من دون اللجوء إلى استعمال النهايات، مما يجعل عملية إيجاد المشتقات أكثر سهولة ودقة. مفهوم أساسي قاعدة مشتقة القوة التعبير اللفظي : قوة x في المشتقة أقل بواحد من قوة x في الدالة الأصلية، ومعامل x في المشتقة يساوي قوة x في الدالة الأصلية. الرموز مثال 2 إذا كان "f(x) = x) ، حيث 11 عدد حقيقي، فإن: 1 - "f(x) = nx . قاعدة مشتقة القوة أوجد مشتقة كل حالة مما يأتي: f(x) = x a f(x) = x⁹ f'(x) = 9x9-1 = 9x8 g(x)=√√x7 (b 8(x) = √x7 7 8(x)=x5 g'(x) = -1 x h(x) = 1(c x h(x) = الدالة المعطاة قاعدة مشتقة القوة بسط الدالة المعطاة أعد كتابة الدالة كقوة نسبية قاعدة مشتقة القوة الدالة المعطاة تنبيه مشتقات القوى السالبة مشتقة f(x) = x لیست f(x) = - 4x3 . تذكر بأننا يجب أن نطرح واحدا من الأس: لنحصل على -4-1=-4+(-1)=-5 لذا فإن f(x) = - 4x5 . h(x)=x-8 h'(x)=-8x-8-1 = - 8 x -9 = -- X 8 تحقق من فهمك أوجد مشتقة كل دالة مما يأتي: j(x) = x² (2A أعد كتابة الدالة كقوة سالبة قاعدة مشتقة القوة بسط (x) = Vx3 (28 m(x)= (2C هناك العديد من قواعد الاشتقاق الأخرى المهمة التي تفيد في إيجاد مشتقات الدوال التي تحوي أكثر من حد. مفهوم أساسي قواعد أخرى للاشتقاق مشتقة الثابت: مشتقة الدالة الثابتة تساوي صفرًا: أي أنه إذا كانت = (f(x، حيث C عدد ثابت ، فإن 0 = (f(x . f'(x) = cnx"-1, مشتقة مضاعفات القوة: إذا كانت "f(x) = cx ، حيث ثابت، و 11 عدد حقيقي، فإن مشتقة المجموع أو الفرق: إذا كانت (f(x) = (x) (x ، فإن : (f(x) = g (x) t h (x . Ministry of Education الدرس 4- المشتقات 201156

إرشادات للدراسة . المشتقات إذا كانت f(x) = x ، فإن 1 = (f(x، وإذا كانت (f(x cx = ، فإن f(x) = c . مثال 3 قواعد الاشتقاق أوجد مشققة كل حالة مما يأتي: f(x) = 5x3 + 4 (a 4 + f(x) = 5x3 الدالة المعطاة 0 + 1 - f(x) = 50 3x3 قواعد مشتقات الثابت ومضاعفات القوى، والمجموع = 15x2 g(x) = x(2x+4) (b بسط (4 + x) = x5(2x3) الدالة المعطاة x) = 2x8 + 4x5) خاصية التوزيع 1 - x) = 2 . 8x8) قاعدتا مشتقتي مضاعفات القوى، والمجموع +4.5x5-1 = 16x7 + 20x4 = h(x) = 5x³-12x+6√√x5 5x³-12x+6√√x5 + 6V h(x)=5x² - 12 + 6 x² x x کر ہے۔ ہے۔ بسط (x) الدالة المعطاة = ( القسم كل حد في البسط على X xxx 6011+ 0 - 1 - 22 - 5 = (x) قواعد مشتقات الثابت، ومضاعفات القوى، والمجموع والفرق -1 1 = 10x + 9x2 = 10x + 97 تحقق من فهمك أوجد مشتقة كل دالة مما يأتي: بسط 4x³-3x²+5x h(x) = (3 x g(x) = 3x4(x+2) (3B - f(x) = 2x5 x3 102 (3A تنبيه الآن ، وبعد أن درست القواعد الأساسية للاشتقاق، يمكنك حل المسائل التي تتطلب حساب ميل مماس المنحنى، أو للتسهيل يمكنك إيجاد كل من إيجاد السرعة المتجهة اللحظية بخطوات أقل، ففي مثال 5 من الدرس 3-4 ، أوجدنا معادلة السرعة المتجهة اللحظية ميل المماس لمنحنى الدالة الجسم متحرك، وستلاحظ الآن سهولة حل المسألة نفسها بتطبيق قواعد الاشتقاق. والسرعة المتجهة اللحظية ومشتقة الدالة، باستخدام القواعد ما لم يُطلب منك استخدام النهايات لإيجاد أي منها. مثال 4 السرعة المتجهة اللحظية تعطى المسافة التي يقطعها جسم بالسنتمترات بعد ثانية بالدالة: 1 - 33 - 18 = (t) ، أوجد معادلة السرعة المتجهة اللحظية (t)) للجسم. السرعة المتجهة اللحظية للجسم هي (t) . s(t) 18t 3t3-1 الدالة المعطاة 0 - 1 - 33 - 3 - 1 - 11 18 = (4) قواعد مشتقات الثابت ومضاعفات القوى، والفرق = 18-92 - بسط أي أن سرعة الجسم المتجهة اللحظية هي: 912 - 18 = ) ، لاحظ أن هذه الإجابة مكافئة لتلك التي حصلت عليها في المثال 5 من الدرس -3 تحقق من فهمك الدالة: 164 - 55 - (61) تمثل الارتفاع بالأقدام بعد ؟ ثانية لكرة قذفت رأسياً إلى أعلى أوجد معادلة . = السرعة المتجهة اللحظية للكرة عند أي زمن . وزارة التعليم 116 الفصل 8 النهايات والاشتقاق Ministry of Education 2024-1446

تنبية
الربط مع الحياة ازدادت سرعة الأفعوانيات حديثا لتصل إلى 120mi/h ، وكذلك ازدادت ارتفاعاتها لتبلغ 450ft النقطة التي تكون عندها مشتقة الدالة صفرًا أو غير موجودة تُسمّى نقطة حرجة للدالة، والنقطة الحرجة قد تشير إلى وجود نقطة قيمة عظمى أو صغرى للدالة ، وتحدثُ عندما يكون ميل مماس منحنى الدالة صفرا أو غير موجود. مفهوم أساسي نظرية القيمة القصوى إذا كانت (f(x متصلة على الفترة المغلقة [a,b] فإن لها قيمة عظمى وصغرى على الفترة [a,b] وذلك إما عند أحد طرفي الفترة أو عند إحدى النقاط الحرجة. y=flx) ' a b y = f(x) a صغری (Lim f(x غير موجودة X-0 التعيين نقاط القيم العظمى والصغرى للدالة على فترة مغلقة، لا بد من حساب قيم الدالة عند أطراف الفترة، وعند النقاط الحرجة في تلك الفترة. مثال 5 من واقع الحياة القيمتان العظمى والصغرى لدالة أفعوانية: الدالة: 1 + 2 4 + 2 14 == 3' = (t) تمثل ارتفاع إبراهيم بالأقدام في أثناء ركوبه أفعوانية، حيث } الزمن بالثواني في الفترة الزمنية [112] ، أوجد أقصى وأدنى ارتفاع يبلغه إبراهيم. أوجد مشتقة (h(t . h(t) = == - 13 + 442 + 11 3 43-1 +4.22-1+0 == =-2+8t الدالة المعطاة (t) قواعد اشتقاق الثابت ومضاعفات القوى، والمجموع، والفرق بسط أوجد النقاط الحرجة بحل المعادلة 0 = (t) . إرشادات للدراسة . دالة كثيرة الحدود مجال تعريف دالة كثيرة الحدود هو مجموعة الأعداد الحقيقية لذلك إذا كانت المشتقة دالة كثيرة حدود فإن النقاط الحرجة توجد فقط عندما تكون المشتقة صفرا ولذلك عند إيجاد القيم العظمى والصغرى لدالة كثيرة حدود (x)) على فترة [a,b] نجد قيم الدالة عند h'(t) = 0 - 12 + St = 0 -t(t-8)=0 اكتب المعادلة h'(t)=-12+8t حلل إذن: 8 = أو 0=t ، وحيث إن 0 = : لا تقع في الفترة [12] ، فإن للدالة نقطة حرجة واحدة عند 8 = E ؛ لذا نحسب قيم (t) عندما 1,812 = . 11 = 89 (1) = - 1 (1)3 + 412 + 1 * h(8)=(8)+4(8)2+. = 7.33 h(12)=(12)+4(12)² + 1 = 3.67 قيمة عظمى قيمة صغرى طرفي الفترة وعند أي قيمة أي أن أقصى ارتفاع يبلغه إبراهيم هو 89ft، وذلك بعد 85، في حين أن أدنى ارتفاع هو 3.67ft تقريبا بعد 12s. لا تكون عندها 0=(f(x . التحقق من الحل التمثيل البياني للدالة: 1 + 42 + 1 - = (h(t المجاور على تحقق من فهمك الفترة [112] باستعمال الآلة البيانية يعزّز هذه النتيجة ، حيث يبين التمثيل البياني أن أعلى ارتفاع يساوي 89 ، ويكون عندما 85 = t. وأدنى ارتفاع يساوي 3.67، ويكون عندما 128=vt nich har (5) رياضة القفز الدالة: 330 + 160 - 2012 = (t) تمثل ارتفاع سعد بالأقدام في أثناء مشاركته في قفزة البنجي (القفز من أماكن مرتفعة، بحيث تكون القدمان موثقتين بحبل مطاطي)، حيث : الزمن بالثواني في الفترة [06] . أوجد أقصى وأدنى ارتفاع يبلغه سعد في هذه الفترة الزمنية. وزارة التعليم Ministry of Education الدرس 4- المشتقات 2011746

الربط مع الحياة: سرعة الافعوانيات
ارشادات للدراسة: دالة كثيرة الحدود
إرشادات للدراسة . قاعدة مشتقة الضرب ينتج عن قاعدة مشتقة الضرب مقدار يمكن تبسيطه. ويمكنك أيضا تركه على حاله من دون تبسيط، ما لم تكن في حاجة إلى تبسيطه. 118 قاعدتا مشتقتَي الضرب والقسمة تعلمت في هذا الدرس أن مشتقة مجموع دالتين تساوي مجموع مشتقتي الدالتين، فهل تكون مشتقة ناتج ضرب دالتين مساويةً لناتج ضرب مشتقتي الدالتين؟ افترض أن: f(x)=x, g(x)=3x3 مشتقة الضرب ضرب المشتقات [f(x) g(x)] = [x 3x³] dx = (3x4)= 12 x³ = d (x) . (3x³) dx = 1.9x2=9x2 f(x)· . dx 8(x) يتضح من هذا المثال أن مشتقة ناتج ضرب دالتين لا تساوي بالضرورة ناتج ضرب مشتقتي الدالتين، ويمكننا استعمال القاعدة الآتية لإيجاد مشتقة ناتج ضرب دالتين. مفهوم أساسي قاعدة مشتقة الضرب إذا كانت مشتقة كل من الدالتين أو 8 موجودة عند x ، فإن : (f(x) gx] = f(x) gx) + f(x) (x) ہے ستبرهن قاعدة مشتقة الضرب في التمرين 48 dx مثال 6 أوجد مشتقة كل حالة مما يأتي: قاعدة مشتقة الضرب h(x) = (x³-2x+7)(3x²-5) (a .h(x) = f(x)g(x): s. f(x) = x³-2x+7, g(x) = 3x²-5:0 من الفرض f(x) = x3 - 2x + 7 2 - f(x) = 3 x2 قواعد مشتقات القوة، ومضاعفات القوى، والثابت والمجموع والفرق g(x)=3x²-5 g'(x)=6x من الفرض قواعد مشتقات مضاعفات القوى، والثابت والفرق استعمل (f(x), f(x), (x), (x لإيجاد مشتقة (x) . h'(x) f'(x) g(x) + f(x) g'(x) =(3x²-2)(3x25) + (x³-2x+7)(6x) = 9x4-15x²-6x² + 10 + 6x4 - 12x² + 42x = 15x4 - 33x2 + 42x + 10 h(x) = (x³-4x²+48x64) (6x2-x-2) (b قاعدة مشتقة الضرب عوض خاصية التوزيع بسط افترض أن: - f(x) = x3 - 4x 2 + 48x - 64, g(x) = 6x2 - x . f(x) = x3 - 4x2 + 48x - 64 f(x) = 3x2 - 8x + 48 - g(x)=6x2-x-2 g'(x)=12x-1 من الفرض قواعد مشتقات القوة، ومضاعفات القوى والثابت والمجموع والفرق من الفرض قواعد مشتقات ومضاعفات القوى والقوة، والثابت والفرق استعمل (f(x), f(x), (x), (x لإيجاد مشتقة (x) . (x) = f(x) (x) + f(x) (x) قاعدة مشتقة الضرب =(3x²-8x+48)(6x2-x-2)+(x³-4x² + 48x64)(12x-1) عوض الفصل 8 النهايات والاشتقاق تحقق من فهمك أوجد مشتقة كل دالة مما يأتي: h(x) = (x² + x3 + x)(8x²+3) (6B h(x) = (x² + 13x²)(7x³- 5x²+18) (6A وزارة التعليم Ministry of Education 2024-1446

بطريقة التبرير نفسها في مشتقة الضرب، يمكنك ملاحظة أن مشتقة ناتج قسمة دالتين لا تساوي ناتج قسمة مشتقتي الدالتين، ويمكن استعمال القاعدة الآتية لحساب مشتقة قسمة دالتين. مفهوم أساسي قاعدة مشتقة القسمة إذا كانت مشتقة كل من الدالتين 8, موجودة عند x ، وكان 0 (x) ، فإن وزارة التعليم Ministry of Education الدرس 4-8 المشتقات 201196 d[f(x) dxgx). = f'(x) g (x) = f (x) g'(x) [g(x)]² ستبرهن قاعدة مشتقة القسمة في التمرين 50 مثال 7 قاعدة مشتقة القسمة أوجد مشتقة كل دالة مما يأتي: 5x2 -3 h(x)= x²-6 f(x) .h(x): = 8(x) افترض أن 6 - f(x) = 5x - 3x = x2 ؛ أي أن: من الفرض f(x) = 10x قواعد مشتقات مضاعفات القوى ، والثابت، والفرق f(x) = 5x2 - 3 (x) = x2 - 6 g'(x) = 2x من الفرض قواعد مشتقات القوة، والثابت، والفرق استعمل (f(x), f(x), (x), (x لإيجاد مشتقة (x) . =(x) قاعدة مشتقة القسمة عوض خاصية التوزيع بسط = f'(x) g(x) = f(x) g'(x) [g(x)]² - 10x(x2 6) (5x2-3)(2x) (x2-6)² 10x3 - 60x - 103 + 6x (x2-6)² = -54x (x2-6)2 h(x)= (b x³-2 إرشادات للدراسة. قاعدة مشتقة القسمة بعد تبسيط ناتج مشتقة القسمة مهما في كثير من التمارين ، إلا أنه ليس من الضروري فك أقواس المقام ما لم ينتج عن ذلك تبسيط أكثر. افترض أن 2 - f(x) = x2 + 8, 8(x) = x3 . 8 + 2 = (f(x من الفرض f(x) = 2x قواعد مشتقات القوة ، والثابت والمجموع 2 - 3 = (x) من الفرض x) = 3x2) قواعد مشتقات القوة، والثابت والفرق استعمل (f(x), f(x), (x), (x لإيجاد مشتقة (x). قاعدة مشتقة القسمة فك الأقواس، ثم بسط 6x k(x) = (78) 2x²+4 h'(x) = f'(x) g(x) f(x) g'(x) [g(x)]² 2x(x32) (x2+8)3x² - (x³-2)2 -x4-24x²-4x = (3-2)2 تحقق من فهمك أوجد مشتقة كل حالة مما يأتي: j(x)= 7x - 10 12x + 5 (7)

تدرب وحل المسائل أوجد مشتقة كل دالة مما يأتي باستعمال النهايات، ثم احسب قيمة المشتقة أوجد مشتقة كل دالة مما يأتي: (مثال 6) عند النقاط المعطاة (مثال (1) f(x) = (4x + 3) (x2) + (9) (22) g(x)=(3x+2x)(5-3x) (23 s(t) (√+2)(311-4) (24 = 8(x) = (x² + 2x) (0.5x+ - 3x) (25 c(t) = (³ + 2tt)(t + 3+4 - 22t) (26 q(a) = - (a+a) (a-13a) (27 f(x) (1.4x5 +2.7x)(7.3x9 -0.8x5) (28 = استعمل قاعدة مشتقة القسمة لإيجاد مشتقة كل دالة مما يأتي: (مثال (7) r(t) = 12+2 (30 3-12 f(m) = 3-2m (29 3 + 201 V + 2x f(x) = m(q)= (32 -x²+3 w+w4 t(w) = (34 9(r)= = 9 +29²+3 93-2 1.53 +5-2 (31 (33 f(x)=4x²-3, x=2,-1 (1 (t) = 2 + 2 + 11, 1 = 5,3 (2) m(j) 14j 13,j=-7,-4 (3 = v(n) 5n2+9n-17, n = 7,2 (4 = r(b) 263-10b, b = -4, -3 (5 = أوجد مشتقة كل دالة مما يأتي : (المثالان (23) z(n) = 2n² + 7n (7 y(f)=-11f (6 2h (8) 1 b(m) = 3m³ - 2m² (9 g(h) = 2h+6h 3. 1 3 01100 - 1+2+3+400 + f(x)=3x2-x2+2x 2 (11 n(t) t = p(k) =k5.28k4.8+3k (13 q(c)=c9-3c5+5c2-3c (12 14) درجات حرارة تُعطى درجة حرارة إحدى المدن بالفهرنهايت في أحد الأيام بالدالة : f(h): =-0.0036 h3 -0.01 h2 + 2.04h+52 حيث عدد الساعات التي انقضت من ذلك اليوم (مثال 4) a) أوجد معادلة تمثل معدّل التغير اللحظي لدرجة الحرارة. ) أوجد معدل التغير اللحظي لدرجة الحرارة عندما : . h = 2, 14, 20 أوجد درجة الحرارة العظمى في الفترة 24 = s h 0 استعمل الاشتقاق لإيجاد النقاط الحرجة، ثم أوجد نقاط القيم العظمى والصغرى لكل دالة مما يأتي على الفترة المعطاة (مثال (5) (35) قام بائع ملابس بإيجاد العلاقة بين سعر قميص، وعدد القطع المبيعة منه يوميا، فوجد أنه عندما يكون سعر القميص ) ريالا ، فإن عدد القطع المبيعة يومياً يساوي 2 - 80 . a) أوجد (d) التي تمثل إجمالي المبيعات اليومية، عندما يكون سعر القميص d ريالا. ) أوجد (d) . أوجد السعر d الذي تكون عنده قيمة المبيعات اليومية أكبر ما يمكن. أوجد مشتقة كل دالة مما يأتي، ثم مثل الدالة والمشتقة بيانيا على المستوى الإحداثي نفسه. (إرشاد يمكنك استعمال الحاسبة البيانية في التمثيل البياني) f(x) = 3x2 + 2x - 7 (36) (x) = VT + 4 (37) f(x) = 45 - 6x3 + 10x - 11 (38 g(x) = (39 f(x)=2x²+8x, [-5,0] (15 r(t) +62-2, [1,4] (16 t(u) u3+15u2+75u + 115, [-6, -3] (17 f(x)=-5x290x, [-11, -8] (18 z(k) k3 3k2 + 3k, [0,3] (19 c(n) =n³+n2-6n+8, [-5, 5] (20 (21) رياضة : عُد إلى فقرة "لماذا؟“ في بداية الدرس. الدالة: 3 + 162 - 65 = ) تمثل ارتفاع الكرة بالأقدام بعد ا ثانية، عندما 4 = 0 ( مثال (5) a) أوجد (t) . أوجد نقاط القيم العظمى والصغرى للدالة (t) في الفترة [04] هل يمكن لأحمد ركل الكرة لتصل إلى ارتفاع 68ft ؟ (40) المشتقات العليا لتكن ( f ( x مشتقة (f(x ، إذا كانت مشتقة (f(x موجودة، فإنها تسمى المشتقة الثانية للدالة ، ويُرمز لها بالرمز (f(x ، أو الرمز (x) (2) ) ، وكذلك إذا كانت مشتقة (x)" موجودة، فإنها تسمى المشتقة الثالثة للدالة ، ويرمز لها بالرمز (f(x أو (x) (3) ، وتسمى المشتقات على هذا النحو المشتقات العليا للدالة في أوجد كلا مما يأتي: المشتقة الثانية للدالة 6 + 23 - f(x) = 4x5 المشتقة الثالثة للدالة : 4x4 - 73 + 10x + 27 = 800 المشتقة الرابعة للدالة: x - 3x - 3 + 2x 2 + 4x2) وزارة التعليم Ministry of Education 2024-1446 الفصل 8 النهايات والاشتقاق 120

قام بائع ملابس بايجاد العلاقة بين سعر قميص وعدد القطع المبيعة، أوجد d التي تمثل إجمالي المبيعات اليومية

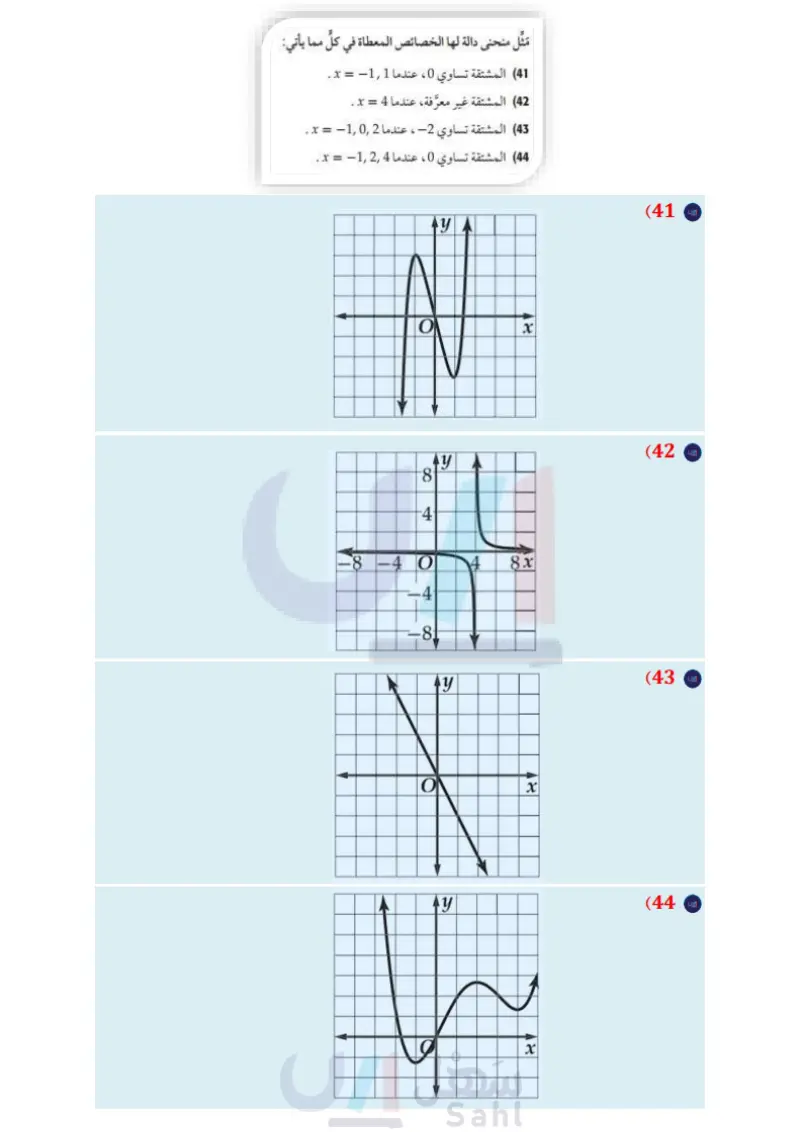
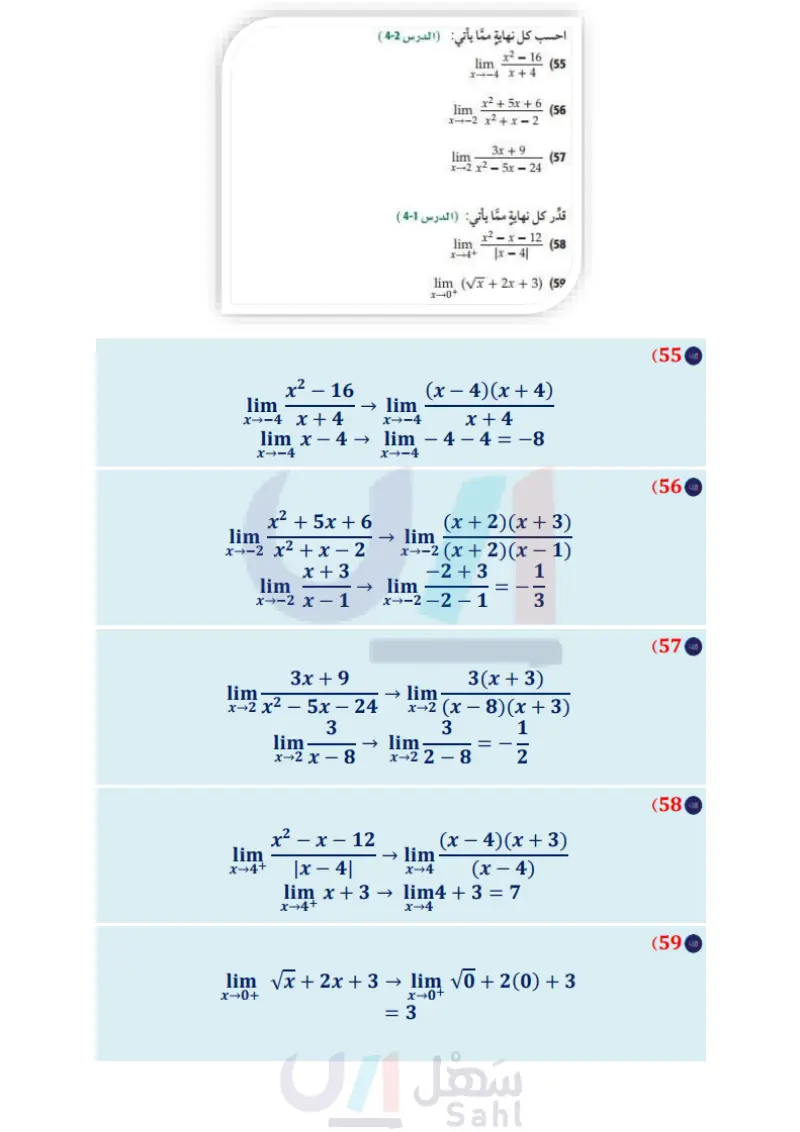
مثل منحنى دالة لها الخصائص المعطاة في كل مما يأتي: (41) المشتقة تساوي 0 ، عندما ,1 = x . (42) المشتقة غير معرفة، عندما 4 = x . (43) المشتقة تساوي 2 ، عندما 102 = x . 44) المشتقة تساوي 0 ، عندما 124 = x . (45) تمثيلات متعددة في هذا التمرين ستستكشف علاقة المشتقات ببعض الخصائص الهندسية للدوال (a) تحليليا أوجد مشتقة صيغة مساحة الدائرة بالنسبة لنصف القطر . 51) اكتب هل من الممكن أن يكون لدالّتين مختلفتين المشتقة نفسها؟ عزز إجابتك بأمثلة. مراجعة تراكمية أوجد ميل مماس منحنى كل دالة مما يأتي عند النقاط المعطاة (الدرس 3-8 ) y=x2 3x, (0, 0), (3,0) (52 y=4-2x, (-2,8), (6, -8) (53 y = x²+9, (3, 18), (6,45) (54 ) لفظيا : وضّح العلاقة بين المعادلة الأصلية ومشتقتها في الفرع 2. احسب كل نهاية مما يأتي: (الدرس 2-8 ) بيانيا : ارسم مربعًا طول ضلعه 2 ، ومكعبا طول ضلعه 24 . تحليليا : اكتب صيغة تمثل مساحة المربع، وأخرى تمثل ح المكعب بدلالة ، ثم أوجد مشتقتي الصيغتين. النقياء وضح العلاقة بين المعادلة الأصلية ومشتقتها في الفرع . مسائل مهارات التفكير العليا (46) اكتشف الخطأ قام كلّ من أحمد وعبدالله بإيجاد 2[ (f(x] للدالة f(x) = 6x 2 + 4x ، حيث كانت إجابة عبد الله: 16 + 144x2 + 96x ، في حين كانت إجابة أحمد: x 3 + 144x2 + 32x 144 ، فأيهما كانت إجابته صحيحة ؟ برر إجابتك. (47) تحد أوجد (y) علما بأن: lim x-4x+4 x²-16 (55 x2 + x + 6 lim x-2 x²+x-2 (56 3x+9 lim x-2 x2-5x-24 (57 قدر كل نهاية مما يأتي: (الدرس 1-8 ) lim x-4+ x2 - x - 12 1x-41 (58 lim (Vx+2x+3) (59 x-0+ تدريب على اختبار h(x)=(-7x2 + 4) (2-x): (60 h'(x)=-14 x A h'(x) = 14 x B h'(x)=-21x2-28x +4 C h'(x) = 21x²-28x-4 D f(y) = 10x2y3 + 5xz2 - 6xy2 + 8x5 - 11xyz 7 (48) برهان برهن صحة قاعدة مشتقة الضرب، بإثبات أن f'(x)g(x) + f(x)g'(x) = lim h-0 f(x + h)g(x + h) - f(x)g(x) h إرشاد: ابدأ بالطرف الأيمن، وأضف ( + )f(x)(x إلى البسط واطرحه منه). (49) تبرير بين ما إذا كانت العبارة الآتية صحيحة أو خاطئة، وبرر إجابتك. "إذا كانت: 3 + 51 f(x) = x ، فإن 2 + f(x) = (5n + (3) x5n" (50) برهان برهن صحة قاعدة مشتقة القسمة، وذلك بإثبات أن: f'(x) g(x) − f(x) g'(x) [g(x)]² lim = h-0 f(x+h) f(x) 8(x + h) h g(x) إرشاد: ابدأ بالطرف الأيمن، ووحد المقامات في البسط، ثم أضف (f(x) (x إلى البسط واطرحه منه). (61) ما ميل مماس منحنی 2 y = 2x عند النقطة (12) 1 A 2B (62) ما مشتقة: 58 = (f(x ؟ 40 f(x) = x 5 4 C 8 D f'(x) = 225 x3 H .... 8 f'(x) = 225 x³ f'(x) = 40 x3 G وزارة التعليم Ministry of Education الدرس 4- المشتقات 2012146




 0
0