الصورة القطبية والصورة الديكارتية للمعادلات - رياضيات3-3 - ثالث ثانوي

الصورة القطبية والصورة الديكارتية للمعادلات رابط الدرس الرقمي www.icn.edu.sa y P(x, y) P(cos 6, sin 0) 10 0 x Polar and Rectangular Forms of Equations 6-2 فيما سبق درست تمثيل النقاط وبعض المعادلات القطبية. (الدرس 1 - 6) والآن . أحول بين الإحداثيات القطبية والديكارتية. . أحول المعادلات من الصورة القطبية إلى الصورة الديكارتية والعكس. لماذا ؟ يبعث مجس مثبت إلى رجل آلي أمواجًا فوق صوتية على شكل دوائر كاملة، وعندما تصطدم الأمواج بجسم، فإن المجس يستقبل إشارة، ويقوم بحساب بعد الجسم عن مقدمة الرجل الآلي بدلالة المسافة المتجهة r ، والزاوية المتجهة ) . ويوصل المجس هذه الإحداثيات القطبية إلى الرجل الآلي الذي يحولها إلى الإحداثيات الديكارتية؛ ليتمكن من تعيينها على خريطة داخلية. الإحداثيات القطبية والديكارتية يمكن كتابة إحداثيات النقطة (x,y) الواقعة على دائرة الوحدة، والمقابلة لزاوية 0 على الصورة ( cos sin) ؛ لأن sin 0 = 1 = =y cos = s 0 = 1 = 1 = =x فإذا كان طول نصف قطر دائرة عددًا حقيقيا r بدلًا من 1، فإنه يمكننا كتابة النقطة (x,y) بدلالة على النحو الآتي: cos 0 = ' sin 0 = r cos 60 = x ' r sin 6 = y اضرب في 7 وإذا نظرنا للمستوى الديكارتي على أنه مستوى قطبي، بحيث ينطبق المحور القطبي على الجزء الموجب من المحور x ، والقطب على نقطة الأصل، فإنه يصبح لدينا وسيلة لتحويل الإحداثيات القطبية إلى الإحداثيات الديكارتية. مفهوم أساسي تحويل الإحداثيات القطبية إلى الإحداثيات الديكارتية إذا كان للنقطة P الإحداثيات القطبية (10) ، فإن الإحداثيات الديكارتية ( ) للنقطة P هي : P(x, y) P(r, e) المحور القطبي .8 x x x = r cos, y = r sin (x, y) = (r cos 0, r sin 0) i تحويل الإحداثيات القطبية إلى الإحداثيات الديكارتية مثال 1 حول الإحداثيات القطبية إلى إحداثيات ديكارتية، لكل نقطة مما يأتي: (4.) بما أن إحداثيات النقطة (4) = ( ) ، فإن 5 = 4,0 = 1 . y = r sin 0 صيغ التحويل = 4 sin r = 4,0= = 4 = 2 (4) بسط x = r cos 0 = 4 cos 唔 = = 2√√3 أي أن الإحداثيات الديكارتية للنقطة ) هي (23) أو (3.462) تقريباً كما في الشكل أعلاه .. وزارة التعليم Ministry of Education الدرس 2-- الصورة القطبية والصورة الديكارتية للمعادلات 2017446

3 R 135° 10 .r=-2,0 = Q(-2, 135°) (b بما أن إحداثيات النقطة (25) = (10) ، فإن 135 y = r sin 0 =-2 sin 135° --9-- صيغ التحويل x = r cos 0 ۲ = -2,0 = 135 =-2 cos 135° بسط = ----√2 = أي أن الإحداثيات الديكارتية للنقطة هي (2-2) أو (1.41141) تقريبا كما في الشكل أعلاه. V(3,-120°) (c بما أن إحداثيات النقطة (3,120) = ( ) ، فإن 120 = 3,0 = r y = r sin 0 صيغ التحويل x = r cos = 3 sin (-120°) r = 3, 0 = 120 = 3 (cos-120°) -120° = -3(-3)--15 =- بسط =- = = 2 -3(-)---- أي أن الإحداثيات الديكارتية للنقطة V ي ( 22-3-) او (2.6 ,1.5) تقريبا كما في الشكل أعلاه. تحقق من فهمك هي حول الإحداثيات القطبية إلى إحداثيات ديكارتية، لكل نقطة مما يأتي: T(-3,45°) (1C 5(5.) (18 R(-6,-120°) (1A إرشادات للدراسة ولكتابة زوج الإحداثيات الديكارتية بالصيغة القطبية، فإنك بحاجة إلى إيجاد المسافة المتجهة r من النقطة (x,y) إلى نقطة الأصل أو القطب، وقياس الزاوية المتجهة التي يصنعها مع الجزء الموجب من المحور x أو المحور القطبي. استعمل نظرية فيثاغورس؛ لإيجاد المسافة 7 من النقطة (x,y) إلى نقطة الأصل. إن العملية المتبعة لتحويل تحويل الإحداثيات P(x, y) 0 π Ox 3 الإحداثيات الديكارتية إلى الإحداثيات القطبية هي ذاتها العملية المتبعة في إيجاد طول المتجه واتجاهه. r² = x² + y² r = √√x² + y² نظرية فيثاغورس خذ الجذر التربيعي الموجب للطرفين ترتبط الزاوية 0 بكل من x y من خلال دالة الظل، ولإيجاد الزاوية 0 tan 0 = 0 = Tan - 1 y تعريف الظل دالة معكوس الظل تذكر أن الدالة العكسية للظل معرفة فقط على الفترة ( 1 - ) أو (9090 - ) في نظام الإحداثيات الديكارتية. وتُعطى قيم 0 الواقعة في الربع الأول أو الرابع أي عندما تكون 70 x ، كما في الشكل 6.2.1 . وإذا كانت 0 > x ، فإن الزاوية تقع في الربع الثاني أو الثالث، لذا عليك إضافة T أو 180 (طول الدورة للدالة y = tan x) إلى قياس الزاوية المعطاة بالدالة العكسية للظل كما في الشكل 6.2.2 T 0+T 0 3 P(x, y) y 1 - Tan = 0 عندما 0 > x وزارة التعليم Ministry of Education 2024-1446 = Tan- + T = 6 أو 180 + * الشكل 6.2.2 3 0 Tan = 0 عندما 0 < x P(x, y) -1 الشكل 6.2.1 الفصل 6 الإحداثيات القطبية والأعداد المركبة 18

مفهوم أساسي تحويل الإحداثيات الديكارتية إلى الإحداثيات القطبية إذا كان للنقطة P الإحداثيات الديكارتية (x,y) ، فإن الإحداثيات القطبية للنقطة ( هي (0) حيث P(.0) P(x, y) y 0 x x 1= =Tan-11/ + = √√x² + y² = 6 ، عندما 0 < x وعندما 0 > x فإن : المحور القطبي. 0 = Tan - 1 أو °180 + 1 Tan = 6 . وعندما 0 = x فإن: 1 = 0 ، r = y إذا كانت 0 < y أو 1 - = 0 ، r = y إذا كانت 0 > y تذكَّر أن هناك عددًا لانهائيا من أزواج الإحداثيات القطبية للنقطة والتحويل من الإحداثيات الديكارتية إلى الإحداثيات القطبية يعطي أحدها. مثال 2 تحويل الإحداثيات الديكارتية إلى الإحداثيات القطبية أوجد زوجين مختلفين كل منهما يمثل إحداثيين قطبيين لكل نقطة معطاة بالإحداثيات الديكارتية في كل مما يأتي: s(1,-√5) بما أن إحداثيات النقطة (3 - (1) = (x,y) ، فإن 3- = x = 1, y . ولأن 0 < x ، لذا استعمل الصيغة 1 - Tan = 0 ؛ لإيجاد الزاوية 0 . 5π 3 6.71 297" + Olv 21 0 = Tan - 1 == Tan-1-V T 3 صيغ التحويل r = Vx2 + 12 x= 1, y = -3 = V12 + (3) 2 = √4=2 بسط أي أن (2) زوج من الإحداثيات القطبية للنقطة S. ويمكن إيجاد زوج آخر باستعمال قيمة موجبة لـ ، وذلك بإضافة 27. فيكون (27 + 3 (2) أو (2) ، كما في الشكل المجاور. T(-3,6) (b - بما أن إحداثيات النقطة (3) = ( x ) ، فإن 6 = x = -3 y ولأن 0 > x ، لذا استعمل الصيغة 180 + 1-Tan = 0 ؛ لإيجاد الزاوية 0 0 = Tan - 1 y = x +180° +180° Tan (-)+ = Tan-1(2) + 180 = 117 y وزارة التعليم Ministry of Education 117° صيغ التحويل r = √√√x² + y² y = 6, x = -3 = (3) 2 + 62 بسط = √√45 = 6.71 أي أن (16.711179 تقريبا هو زوج من الإحداثيات القطبية للنقطة T ، ويمكن إيجاد زوج آخر باستعمال قيمة سالبة لـ ، فنحصل على (180° + 117° ,6.71 - ) أو ( 6.71,297 - ) ، كما في الشكل المجاور. تحقق من فهمك أوجد زوجين مختلفين كل منهما يمثل إحداثيين قطبيين لكل نقطة معطاة بالإحداثيات الديكارتية في كل مما يأتي: W(-9,-4) (2B الدرس 2-- الصورة القطبية والصورة الديكارتية للمعادلات 201946 V(8,10) (2A

في بعض ظواهر الحياة الطبيعية ، قد يكون من المفيد أن تحوّل بين الإحداثيات القطبية والإحداثيات الديكارتية. مثال 3 من واقع الحياة التحويل بين الإحداثيات رجل آلي بالرجوع إلى فقرة «لماذا؟» ، افترض أن الرجل الآلي متجه إلى الشرق، وأن المِجَسَّ قد رَصَدَ جسما عند النقطة (5295) . a ما الإحداثيات الديكارتية التي يحتاج الرجل الآلي إلى حسابها ؟ y = r sin 0 صيغ التحويل x = r cos 0 = 5 sin 295° r = 5, 0 = 295 = 5 cos 295° =-4.53 بسط 2.11 الربط مع الحياة صممت وكالة ناسا رجلا آليا وزنه 3400 باوند، وطوله 12ft، وطول ذراعه ft 11 لأداء بعض المهام في الفضاء الخارجي. أي أن الإحداثيات الديكارتية لموقع الجسم هي (4.53 - 2.11) تقريبا. إذا كان موقع جسم رُصد سابقا عند النقطة التي إحداثياتها (37) ، فما المسافة وقياس الزاوية بين الجسم والرجل الآلي؟ 0 = Tan -1 1/ -17 = Tan - = 66.8° صيغ التحويل x=3,y=7 بسط r = √√x² + y² = √√3² + 72 = 7.62 الإحداثيات القطبية لموقع الجسم هي (66.8 (7.62) تقريباً ؛ أي أن المسافة بين الجسم والرجل الآلي 7.62، وقياس الزاوية بينهما 66.8 تحقق من فهمك 3) صيد الأسماك: يُستعمل جهاز رصد؛ لتحديد موقع وجود الأسماك تحت الماء. افترض أن قاربا يتجه إلى الشرق، وأن جهاز الرصد قد رصد سربًا من الأسماك عند النقطة (6,125). ما الإحداثيات الديكارتية لموقع سرب الأسماك ؟ إذا كان موقع سرب الأسماك قد رصد سابقا عند النقطة التي إحداثياتها الديكارتية (26) ، فما الإحداثيات القطبية لموقع السرب؟ المعادلات القطبية والديكارتية قد تحتاج في دراستك المستقبلية إلى تحويل المعادلة من الصورة الديكارتية إلى الصورة القطبية والعكس؛ وذلك لتسهيل بعض الحسابات. فبعض المعادلات الديكارتية المعقدة صورتها القطبية أسهل كثيرا. لاحظ معادلة الدائرة على الصورة الديكارتية والقطبية كما في الشكل أدناه. وزارة التعليم Ministry of Education 2024-1446 المعادلة على الصورة القطبية r = 3 플 3- 2 المعادلة على الصورة الديكارتية x2 + y2 = 9 وبشكل مماثل فإن بعض المعادلات القطبية المعقدة صورتها الديكارتية أسهل كثيرا، = r صورتها الديكارتية هي 6 = 2x - 3y 6 2 cos 0 - 3 sin 0 فالمعادلة القطبية : الفصل 6 الإحداثيات القطبية والأعداد المركبة 20

إرشادات للدراسة المتطابقات المثلثية من المفيد أن تراجع المتطابقات المثلثية التي تعلمتها سابقا لمساعدتك على تبسيط الصورة القطبية للمعادلات الديكارتية إن عملية تحويل المعادلة من الصورة الديكارتية إلى الصورة القطبية عملية مباشرة؛ إذ نعوض عن x بـ 6 r cos، وعن لا بـ 0 r sin ، ثم نبسط المعادلة الناتجة باستعمال الطرق الجبرية والمتطابقات المثلثية. مثال 4 تحويل المعادلات الديكارتية إلى المعادلات القطبية اكتب كل معادلة مما يأتي على الصورة القطبية: (x - 42 + y = 16 (2) لإيجاد الصورة القطبية للمعادلة، عوض عن x بـ 0 r cos وعن y بـ 0 r sin . ثم بسط المعادلة. المعادلة الأصلية x = r cos 6, y = r sin 0 اضرب r² cos²0- (x-4)² + y² = 16 (r cos 0-4)2 + (r sin 0)² = 16 . 8r cos 6 + 16 + 12 sin2 0 = 16 2 cos2 0 - 8r cos 6 + 2 sin2 0 = 0 2 cos2 0 + 12 sin2 0 = 8r cos 2 (cos2 0 + sin2 0 = 8r cos r² (1) = 8r cos 0 r = 8 cos 0 y= x² (b y = x² المعادلة الأصلية x = r cos 0, y = r sin 0 r sin 0 = (r cos 02 اضرب r sin 0 = 2 cos2 0 = 1 sin cos20 اقسم الطرفين على r cos20 اطرح 16 من الطرفين ضع الحدود المربعة في طرف واحد حلل متطابقة فيثاغورس اقسم الطرفين على 7 حيث 0 r sin 4 sin 6 cos² 0 cos cos sin 1 . =r cos e cos e المتطابقات النسبية ومتطابقات المقلوب tan 10 sec 6 = r تحقق من فهمك اكتب كل معادلة مما يأتي على الصورة القطبية : x2 + (y - 32 = 9 (4) x2 - 12 = 1 (48 المعادلة الديكارتية إلى عملية تحويل المعادلة القطبية إلى معادلة ديكارتية ليست مباشرة مثل عملية التحويل من | المعادلة القطبية، ففي التحويل الثاني تلزمنا جميع العلاقات الآتية: . 2 = x2 + y2, tan 0 = 3 x = r cos , y = r sin 0 وزارة التعليم Ministry of Education الدرس 2-- الصورة القطبية والصورة الديكارتية للمعادلات 2021446

وزارة التعليم Ministry of Education 2024-1446 مثال 5 تحويل المعادلات القطبية إلى المعادلات الديكارتية اكتب كل معادلة قطبية مما يأتي على الصورة الديكارتية. المعادلة الأصلية خذ tan الطرفين tan 6 = اضرب الطرفين في x المعادلة الأصلية اضرب الطرفين في 7 2 = x2 + y , y = r sin 0 أضف 5 إلى الطرفين المعادلة الأصلية ربع الطرفين r² = x²+ y² 0 = (a tan 0 = 3 3 r = 7 (b r = 7 2 = 49 x2 + y2 = 49 r = -5 sin 0 (c r = -5 sin 0 2 = -5r sin 0 x2 + y2 = -5y x2 + y2 + 5y = 0 تحقق من فهمك اكتب كل معادلة قطبية مما يأتي على الصورة الديكارتية: r 3 cos 0 (5C = (58) 7 = -3 (5 إرشادات للدراسة طريقة بديلة النقطتان (2) و (4) تقعان على المستقيم = 8 والإحداثيات الديكارتية لهما . (2√√3,2), (√3,1) فتكون معادلة المستقيم المار بهاتين النقطتين هي: √3 y=x الفصل 6 الإحداثيات القطبية والأعداد المركبة 22

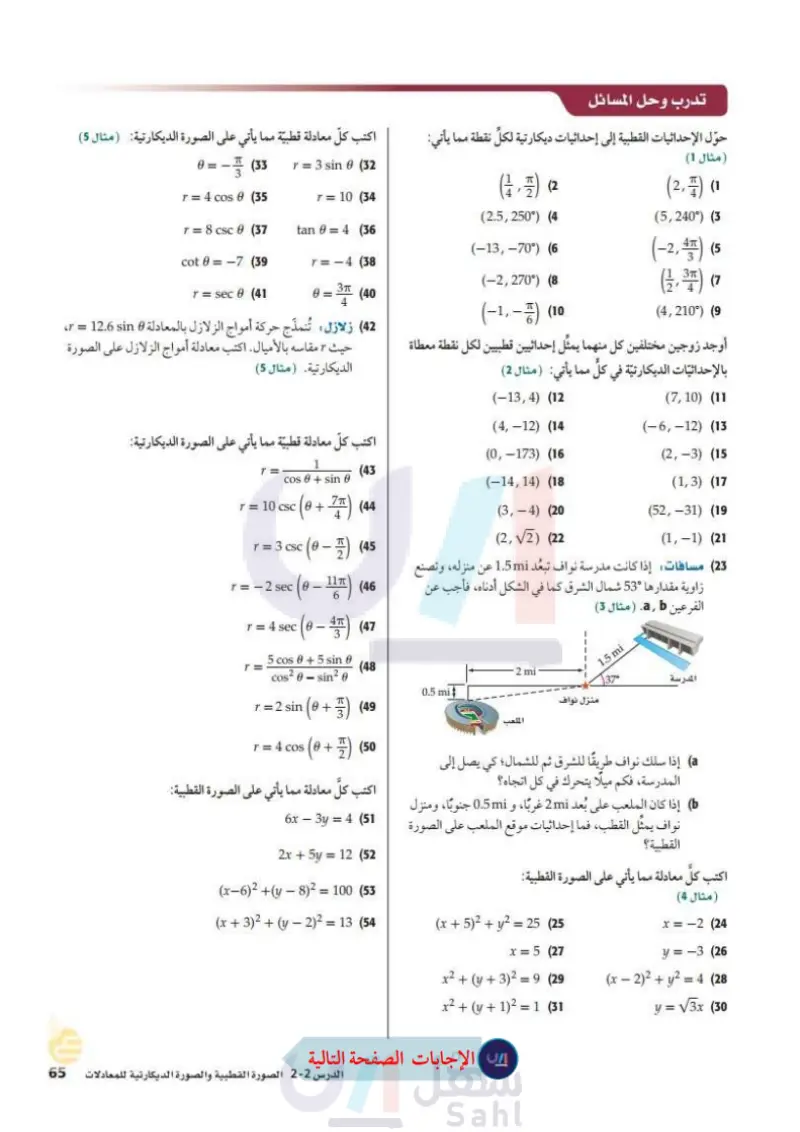
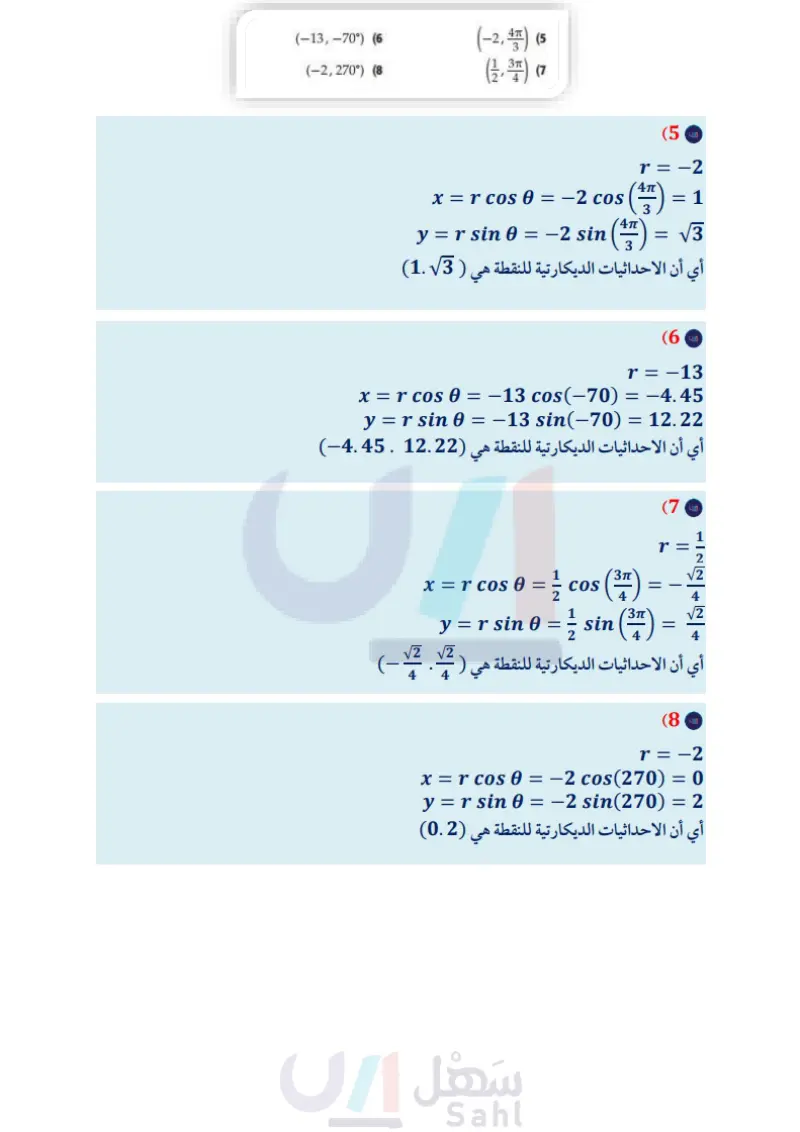
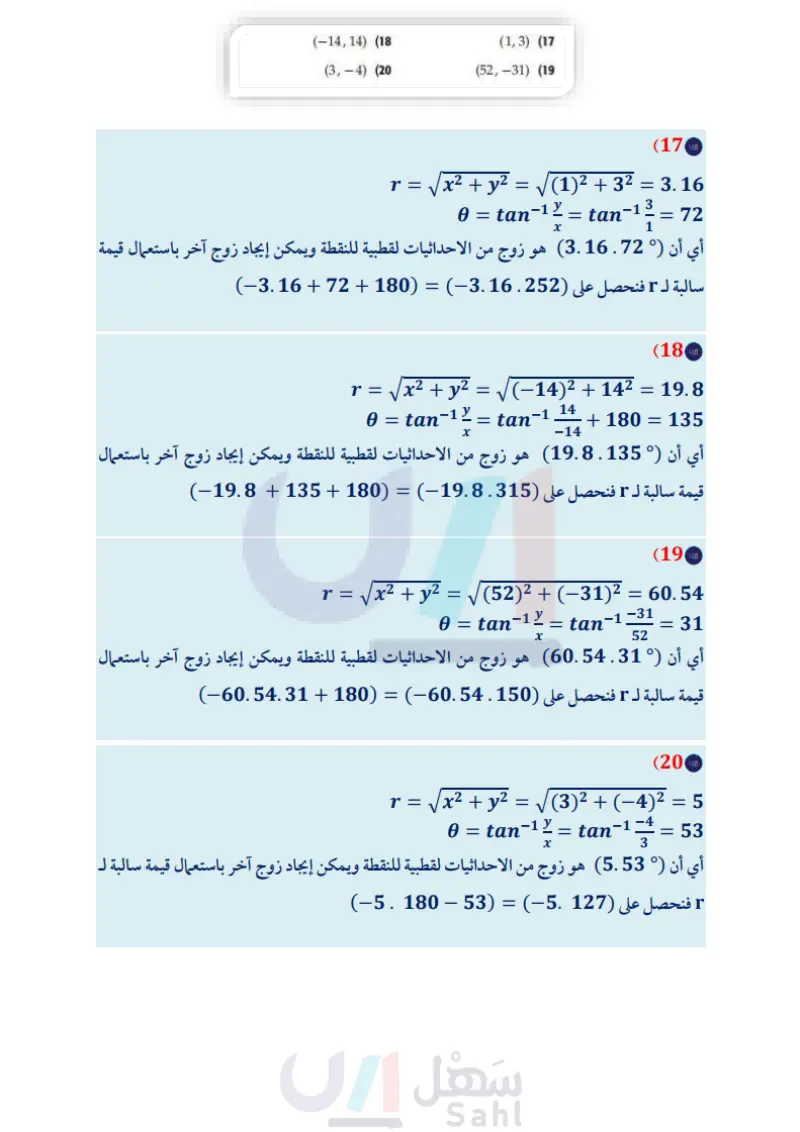
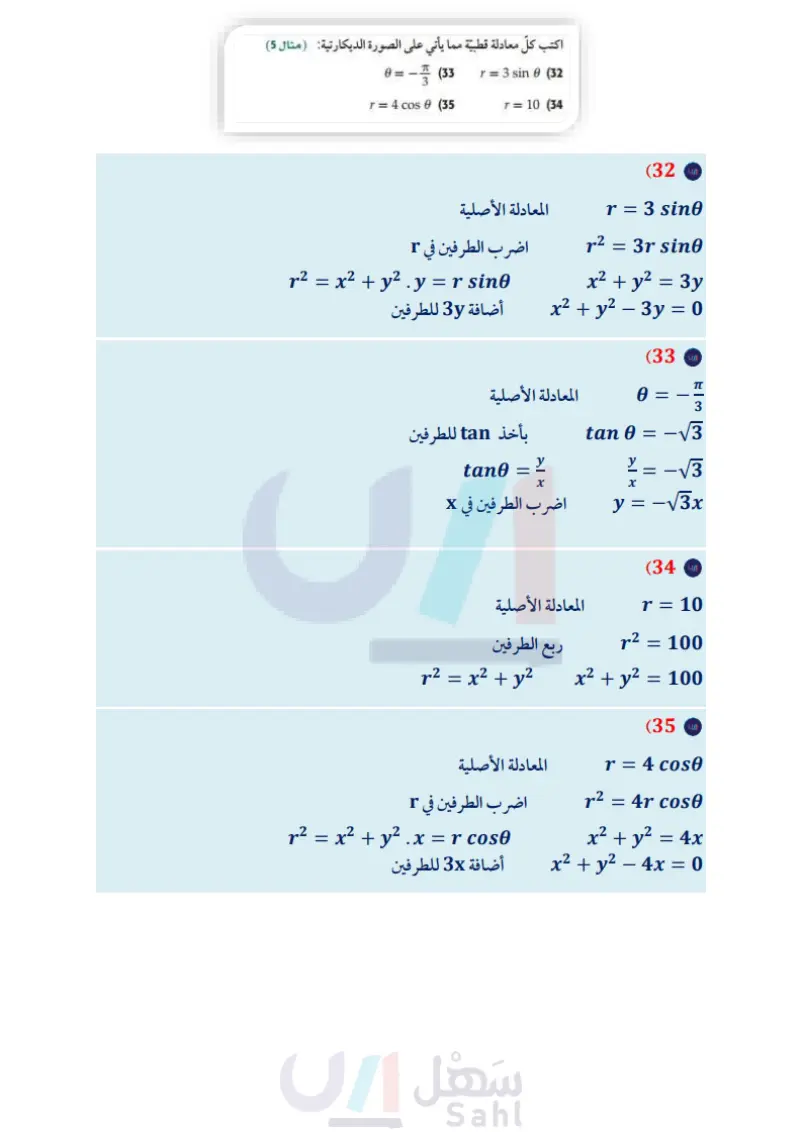
تدرب وحل المسائل اكتب كلّ معادلة قطبية مما يأتي على الصورة الديكارتية (مثال (5) حول الإحداثيات القطبية إلى إحداثيات ديكارتية لكل نقطة مما يأتي: (مثال (1) r = 3 sin 6 (32) (-) (2 (2, 1) (1 (2.5,250°) (4 (5,240°) (3 (-13,-70°) (6 (-2,270°) (8 (-1,-) (10 (-2, 4) (5 (1,3) (7 (4,210°) (9 أوجد زوجين مختلفين كل منهما يمثل إحداثيين قطبيين لكل نقطة معطاة بالإحداثيات الديكارتية في كل مما يأتي: (مثال 2) (7, 10) (11 (-6,-12) (13 (2,-3) (15 (1,3) (17 (52,-31) (19 (1,-1) (21 (-13,4) (12 0=-(33 r = 4 cos 0 (35 r = 10 (34 r = 8 csc 0 (37 tan 0=4 (36 cot =-7 (39 r = -4 (38 r = sec 6 (41 0 = 3 (40 (42) زلازل: تُنمذج حركة أمواج الزلازل بالمعادلة 0 r = 12.6 sin، حيث r مقاسه بالأميال. اكتب معادلة أمواج الزلازل على الصورة الديكارتية (مثال (5) اكتب كل معادلة قطبية مما يأتي على الصورة الديكارتية (4,-12) (14 (0,-173) (16 (43) (-14, 14) (18 (3,-4) (20 (2,√2) (22 (23) مسافات إذا كانت مدرسة نواف تبعد 1.5mi عن منزله، وتصنع زاوية مقدارها 53" شمال الشرق كما في الشكل أدناه، فأجب عن الفرعين a, b (مثال (3) المدرسة 1.5 mi 37 T= 1 cos 8 + sin 0 r = 10 csc | 0 + (0+7) (44 r = r = 3 csc (0 - ) (45 117 -2sec (0-1) (46 r = 4 sec 0 4x (0-4) T= 3 5 cos 0 + 5 sin 0 cos² - sin² 0 r = 2 sin (0+) (49 r = 4 cos (0 + 1 ) (50 (47 (48 2.mi 0.5 mi منزل نواف الملعب a إذا سلك نواف طريقًا للشرق ثم للشمال؛ كي يصل إلى المدرسة، فكم ميلا يتحرك في كل اتجاه؟ إذا كان الملعب على بعد 2mi غربا، و 0.5mi جنوبا، ومنزل نواف يمثل القطب، فما إحداثيات موقع الملعب على الصورة القطبية؟ اكتب كل معادلة مما يأتي على الصورة القطبية : (مثال (4) x = -2 (24 y = -3 (26 (x-2)² + y²=4 (28 y = √√3x (30 اكتب كل معادلة مما يأتي على الصورة القطبية : 6x-3y=4 (51 2x+5y=12 (52 (x-6)²+(y-8)² = 100 (53 (x+3)²+(y-2)² = 13 (54 (x + 52 + y2 = 25 (25) x = 5 (27 x2 + y + 32 = 9 (29) x2 + y + 12 = 1 (31 وزارة التعليم Ministry of Education الدرس 2-- الصورة القطبية والصورة الديكارتية للمعادلات 20236

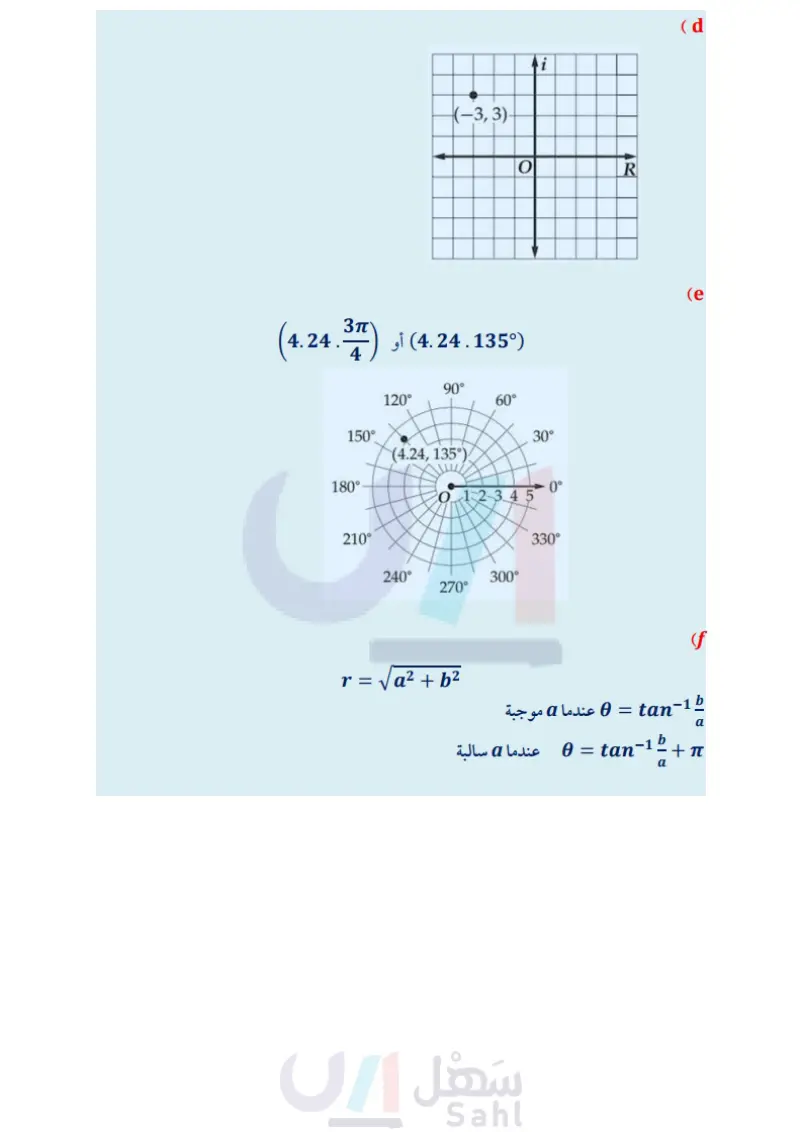
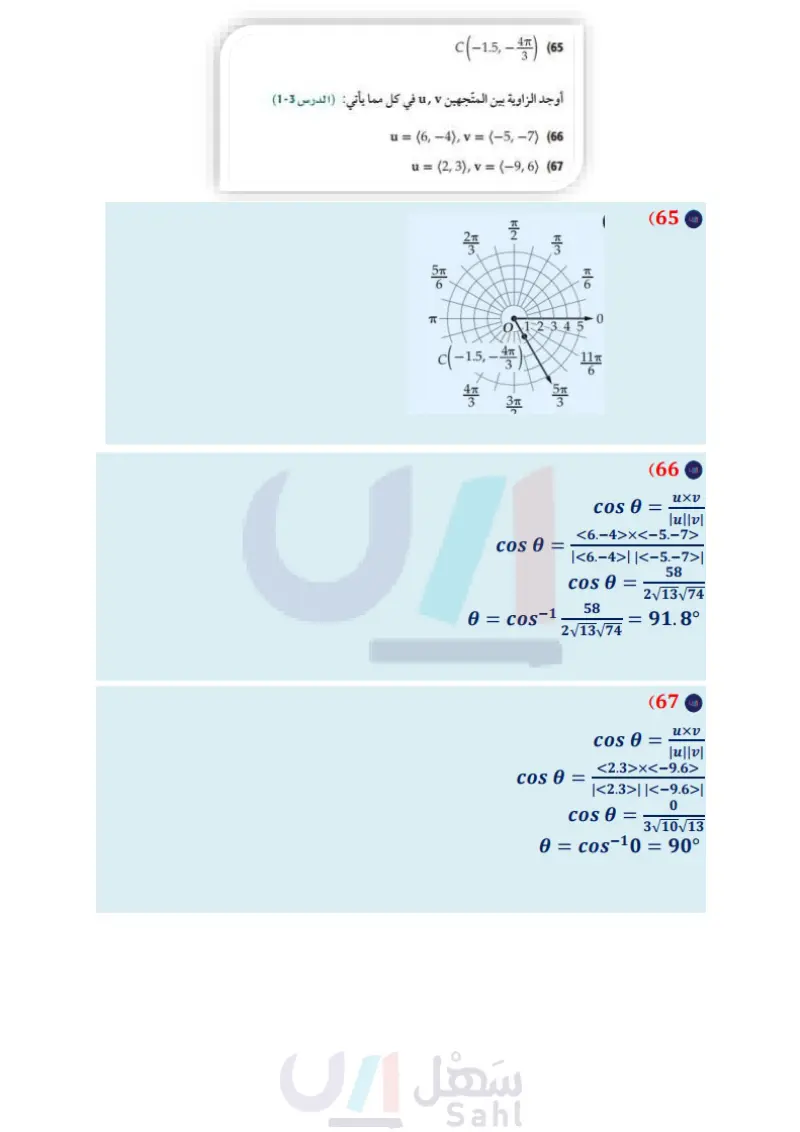
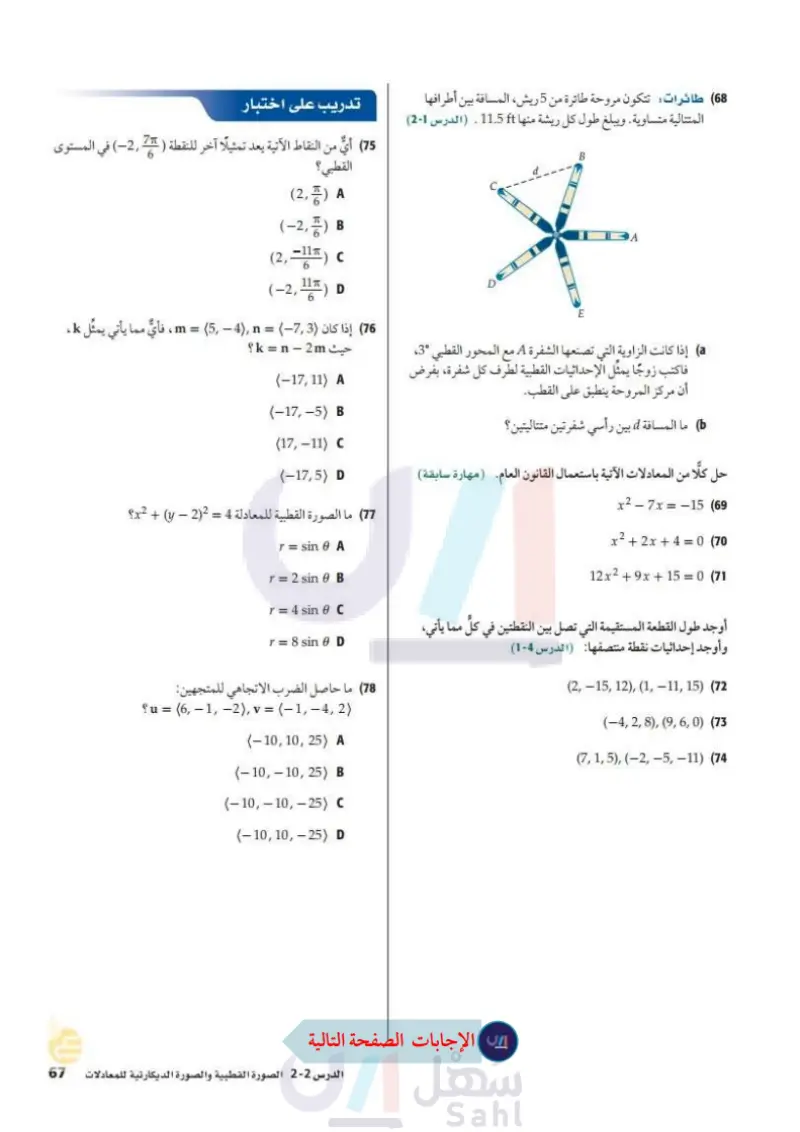
(55) جولف في أحد ملاعب الجولف، يحيط بثقب الهدف منطقة خضراء محاطة بمنطقة رملية، كما في الشكل أدناه أوجد مساحة مسائل مهارات التفكير العليا المنطقة الرملية على فرض أن الثقب يمثل القطب لكلتا المعادلتين، وأن المسافات تُقاس بوحدة الياردة. T=6 cos 0+2 sin x7 + y - 6x - 2 = 39 (58) اكتشف الخطأ يحاول كل من باسل وتوفيق كتابة المعادلة القطبية 0 r = sin على الصورة الديكارتية ، فيعتقد توفيق أن الحل هو + ( - 1 = 1 + 2، في حين يعتقد باسل أن الحل هو y = sin x . أيهما كانت إجابته صحيحة ؟ برر إجابتك. (59) تحد اكتب معادلة الدائرة 6 2a cos = " بالصورة الديكارتية، وأوجد مركزها وطول نصف قطرها. (56) عجلة دوارة إذا كانت إحداثيات أدنى نقطة في عجلة دوارة 60 اكتب اكتب تخمينا يبين متى يكون تمثيل المعادلة على الصورة (0 ,0)، وأعلى نقطة فيها (020). فاكتب معادلة العجلة الدوارة الموضحة بالشكل المجاور على الصورة الديكارتية. ) اكتب المعادلة في الفرع a بالصيغة القطبية. (0,20) القطبية أسهل من تمثيلها على الصورة الديكارتية، ومتى يكون العكس صحيحًا. (61) برهان: استعمل 0 x = r cos, y = r sin ؛ لإثبات أن 0 sec 10, r = y csc ، حيث 0 0 sin 0 ± 0, cos (0,0) (62) تحد اكتب المعادلة: r2(4 cos² + 3 sin2 0) + r(-8a cos 0+ 6b sin 0) = 12-4a²-362 (57) تمثيلات متعددة في هذه المسألة سوف تكتشف العلاقة بين الأعداد المركبة والإحداثيات القطبية a بيانيا يمكن تمثيل العدد المركب a + bi في المستوى الديكارتي بالنقطة (a). مثل العدد المركب 8i + 6 في المستوى الديكارتي. 6 عدديا أوجد الإحداثيات القطبية للعدد المركب باستعمال الإحداثيات الديكارتية التي أوجدتها في الفرع a . بيانيا : عزّز إجابتك في الفرع b بتمثيل الإحداثيات القطبية في المستوى القطبي. بيانيًا مثل بيانيا العدد المركب 3 + 3 في المستوى الديكارتي بيانيا : أوجد الإحداثيات القطبية للعدد المركب باستعمال الإحداثيات الديكارتية التي أوجدتها في الفرع d. ومثل الإحداثيات القطبية في المستوى القطبي. تحليليا أوجد العبارات الجبرية التي تبين كيفية كتابة العدد المركب a + bi بالإحداثيات القطبية. على الصورة الديكارتية (إرشاد؛ فك الأقواس قبل تعويض قيم 12 ، . تمثل المعادلة الديكارتية قطعا مخروطيا). مراجعة تراكمية مثل كل نقطة مما يأتي في المستوى القطبي. (مهارة سابقة) A(-2,45°) (63 D (1,315°) (64 c(-1.5-1) 165 V أوجد الزاوية بين المتجهين , في كل مما يأتي: (مهارة سابقة) u = (6,-4), v = (-5,-7) (66 u = (2,3), v = (-9,6) (67 24 الفصل 6 الإحداثيات القطبية والأعداد المركبة وزارة التعليم Ministry of Education 2024-1446

68 طائرات تتكون مروحة طائرة من 5 ريش، المسافة بين أطرافها المتتالية متساوية. ويبلغ طول كل ريشة منها ft 11.5 . الدرس (1-6) B تدريب على اختبار 75) أني من النقاط الآتية بعد المليلا أخر للنقطة ( 21 (2) في المستوى القطي؟ (2,1) A (-2,7) B (2,-11) C (-2) D E إذا كانت الزاوية التي تصنعها الشفرة A مع المحور القطبي 3، فاكتب زوجاً يمثل الإحداثيات القطبية لطرف كل شفرة، بفرض أن مركز المروحة ينطبق على القطب. ما المسافة ، بين رأسي شفرتين متتاليتين؟ حل كلا من المعادلات الآتية باستعمال القانون العام (مهارة سابقة) x2 - 7x = -15 (69) x 2 + x + 4 = 0 (70 12x²+9x+150 (71 (76) إذا كان (73) = 4 = m ، فأي مما يأتي يمثل k، حيث k = n - 2m (-17,11) A (-17,-5) B (17,-11) C (-17,5) D (77) ما الصورة القطبية للمعادلة 4 - 22 - x 2 + (y؟ r = sin A r = 2 sin 0 B وزارة التعليم Ministry of Education أوجد طول القطعة المستقيمة التي تصل بين النقطتين في كل مما يأتي، وأوجد إحداثيات نقطة منتصفها (مهارة سابقة) r = 4 sin 0 C r = 8 sin 0 D 78 ما حاصل الضرب الاتجاهي للمتجهين: fu (6,-1,-2), v = (-1,-4, 2) (-10, 10, 25) A (-10, -10, 25) B (-10, 10, 25) C (-10, 10, 25) D الدرس 2-- الصورة القطبية والصورة الديكارتية للمعادلات 20256 (2,-15, 12), (1, -11, 15) (72 (-4, 2, 8), (9,6, 0) (73 (7, 1, 5), (-2, -5, -11) (74