التوزيعات ذات الحدين - رياضيات3-3 - ثالث ثانوي

7-6 فيما سبق التوزيعات ذات الحدين Binomial Distributions لماذا ؟ www.icn.edu.sa الحدين (مهارة سابقة) درست استعمال نظرية ذات في لعبة الكرة الطائرة تبين أن اللاعب سلمان ينجح في لعب الإرسال الساحق الذي لا يصده الخصم في %36 من محاولاته، وبذلك يحصل فريقه على نقطة في كل مرة ينجح فيها. والان أميز تجربة ذات الحدين أجد الاحتمالات باستعمال التوزيع ذي الحدين ومفكوكه. المفردات: تجربة ذات الحدين binomial experiment التوزيع ذو الحدين binomial distribution 17 التوزيع ذو الحدين كثير من التجارب الاحتمالية يكون لها نتيجتان فقط؛ نجاح أو فشل أو يمكن جعلها كذلك. فمثلا في مسائل الاختيار من متعدد التي لها 5 إجابات، يمكن تصنيف نتائج الإجابة عن كل فقرة إلى صح، أو خطأ، ويمكن تصنيف نتائج دواء طبي على أنه فعّال أو غير فعال. مفهوم أساسي تجربة ذات الحدين تجربة ذات الحدين هي تجربة احتمالية تحقق الشروط الآتية: • يُعاد إجراء التجربة لعدد محدد (1) من المحاولات المستقلة (المرات) . كل محاولة لها فقط نتيجتان متوقعتان نجاح 5 ، أو فشل F . . (S) "ويرمز له بالحرف p" هو نفسه في كل محاولة. واحتمال الفشل (P(F "ويرمز له بالحرف q" هو نفسه في كل محاولة ويساوي p - 1 . ويُمثل المتغير العشوائي X عدد مرات النجاح في 11 من المحاولات. 72 الفصل 7 الاحتمال والإحصاء مثال 1 تمييز التجربة ذات الحدين حدد ما إذا كانت كل تجربة مما يأتي ذات حدين، أو يمكن جعلها كذلك. وإذا كانت تجربة ذات حدين، فاكتب قيم ، وقيم المتغير العشوائي الممكنة، وإذا لم تكن كذلك فبين السبب. تبين نتيجة لمسح إحصائي داخل إحدى المدارس أن 68% من الطلاب يمتلكون حاسبة بيانية. إذا تم اختيار 6 طلاب عشوائيا، وسؤالهم عما إذا كانوا يمتلكون هذه الآلة؛ وكان المتغير العشوائي X يُمثل عدد الطلاب الذين يملكون الحاسبة البيانية، فإن هذه التجربة تحقق شروط تجربة ذات الحدين وهي: • كل طالب تم اختياره يُمثل محاولة، وعملية اختيار الطلاب السنة تتكون من محاولات مستقلة. للتجربة نتيجتان متوقعتان الطالب يملك الحاسبة البيانية ، أو لا يملكها F . . احتمال النجاح نفسه لكل طالب تم اختياره 0.68 = (S) . وفي هذه التجربة 0.68 = (5) = n = 6, p . احتمال الفشل g = 1 - p ، أي أن: 0.32 = 0.68 - 1 = 1 . ويُمثل X عدد الطلاب الذين يملكون حاسبة بيانية من الذين تم اختيارهم، أي أن: X=0,1,2,3,4,5,6 (6) يحتوي صندوق على 52 بطاقة، وخُصص لكل 13 بطاقة أحد الألوان الآتية: الأحمر، الأسود، الأخضر، الأبيض. سحبت منه 5 بطاقات الواحدة تلو الأخرى دون إرجاع. وكان المتغير العشوائي X يدل على عدد البطاقات المسحوبة ذات اللون الأخضر. في هذه التجربة، كل بطاقة يتم سحبها تُمثل محاولة، وبما أنه يتم الاحتفاظ بالبطاقة التي تم اختيارها السحب دون إرجاع)، فإن المحاولات غير مستقلة، واحتمال النجاح في كل محاولة يختلف عن الأخرى؛ وزارة التعليم لذا فإن هذه التجربة ليست ذات حدين Ministry of Education 2024-1446

تحقق من فهمك حدد ما إذا كانت كل تجربة مما يأتي ذات حدين، أو يمكن جعلها كذلك. وإذا كانت تجربة ذات حدين، فاكتب قيم ، وقيم المتغير العشوائي الممكنة، وإذا لم تكن كذلك فبين السبب. 1) أظهرت نتيجة لمسح إحصائي في إحدى المدارس ذات الزي الموحد أن %61 يحبون الزي الجديد، وأن %24% لا يحبونه. إذا تم اختيار 20 طالبًا بشكل عشوائي، وسؤالهم عما إذا كانوا يحبون الزي الجديد. وكان المتغير العشوائي X يدل على عدد الطلاب الذين يحبون الزي الجديد. (18) أجاب خالد عن اختبار مكوّن من 20 فقرة من نوع الاختيار من متعدد لكل فقرة منها أربع إجابات، واحدة فقط صحيحة (دون معرفة علمية بموضوع الاختبار). وكان المتغير العشوائي X يدل على عدد الإجابات الصحيحة. يُسمى توزيع النتائج المتوقعة لتجربة ذات حدين والاحتمالات المرتبطة بها توزيع ذات الحدين. ويمكن حساب الاحتمالات في هذا التوزيع باستعمال الصيغة لا - الي الا ويوكي التي تمثل حدا في مفكوك اياها. مفهوم أساسي -x صيغة احتمال ذات الحدين احتمال النجاح في X مرة من 11 من المحاولات المستقلة في تجربة ذات الحدين هو: X-X = ! P(X) = Cxpg" - (n - X!X! Xn-X Pxq"- إرشاد تقني حيث p احتمال النجاح ، و احتمال الفشل في المحاولة الواحدة. مثال 2 من واقع الحياة التوزيع ذو الحدين اختبار في اختبار نهائي، أكد 35% من الطلاب أنهم أجابوا بشكل اعتيادي. إذا اختير 5 طلاب عشوائيا، وتم سؤالهم عما إذا أدوا الاختبار بشكل اعتيادي. وكان المتغير العشوائي X يدل على عدد الطلاب الذين أجابوا بنعم ن السؤال ، فكوّن جدولا للتوزيع ذي الحدين، ومثله بالأعمدة، ثم أوجد احتمال أن يجيب 3 طلاب على الأقل عن السؤال بنعم. عن هذه تجربة ذات حدين فيها : 0.65 = 0.35 - 1 = 1 ,0.35 = n = 5, p . استعمل الحاسبة البيانية TI-nspire؛ حساب احتمال ذات الحدين الحساب احتمال كل قيمة ممكنة من قيم X مستعملا صيغة احتمال ذات الحدين. لإيجاد كل احتمال لذات الحدين على الحاسبة البيانية استعمل الأمر binomPdf(n, p, x) قائمة تطبيق الحاسبة . مثال: لإيجاد (1) p اكتب (0.351 ,5) binomPdf ثم اضغط Enter فتحصل على 0.312386 كما يمكن إيجادها باستعمال الآلة الحاسبة العلمية كما يأتي: اضغط على المفاتيح الآتية من اليسار إلى اليمين P(1) = 5C (2) = (0) = Co. 0.350 . 0.655 = 0.116 0.351 . 0.654 = 0.312 C2 . 0.352 . 0,653 = 0.336 (3) = C3 0 0.353 . 0,652 = 0.181 P(4) = C4 0 0.354 . 0.651 = 0.049 = P(5) C 0.355.0.650 = 0.005 وفيما يأتي جدول التوزيع ذي الحدين للمتغير x ، وتمثيله بالأعمدة. عدد الذين أدوا الاختبار بشكل اعتيادي وزارة التعليم Ministry of Education P(X) 0.35 0.3 0.25 0.2 50.15 0.1 0.05 01234 عدد الطلاب الدرس 6-7 التوزيعات ذات الحدين 20736 x P(X) 0 0.116 1 0.312 2 0.336 3 0.181 4 0.049 5 0.005 5 5 SHIFT + 1 0.35 0.35 0.3123859315 فتظهر الشاشة

إرشادات للدراسة اختيار الاحتمالات أحيانا يكون من الأسهل أن تجد احتمال الفشل وتطرح هذه النتيجة من 1 لتجد لأنهما احتمال النجاح احتمالان متتامان 74 لإيجاد احتمال أن 3 طلاب على الأقل أجابوا بنعم، أوجد (5) + (4) + (3) . (5) + (4) + (3) = (3) )X) احتمال 3 طلاب على الأقل 0.181 +0.049 +0.005 =0.235=23.5% تحقق من فهمك P(3) = 0.181, P(4) = 0.049, P(5) = 0.005 بسط (2) كليات يدرس في إحدى الكليات 48% من الطلاب لغة عالمية خلال سنة التخرج. إذا اختير 7 خريجين عشوائيا، وتم سؤالهم عما إذا درسوا لغة عالمية في سنتهم الأخيرة. وكان المتغير العشوائي X يدل على عدد الطلاب الذين أجابوا بنعم، فكون التوزيع ذا الحدين، ومثله بالأعمدة، ثم أوجد احتمال أن يجيب أقل من 4 طلاب بنعم. تستعمل الصيغ الآتية؛ لإيجاد المتوسط والتباين والانحراف المعياري للتوزيع ذي الحدين. مفهوم أساسي المتوسط والتباين والانحراف المعياري للتوزيع ذي الحدين يحسب المتوسط والتباين والانحراف المعياري لمتغير عشوائي X في التوزيع ذي الحدين بالصيغ الآتية: المتوسط الفصل 7 الاحتمال والإحصاء التباين الانحراف المعياري H = np σ²=npq 0 = V2 = Vmpa مثال 3 المتوسط والتباين والانحراف المعياري للتوزيع ذي الحدين اختبار بالرجوع إلى تجربة ذات الحدين في المثال .2 . أوجد المتوسط والتباين والانحراف المعياري للمتغير العشوائي ، ثُمَّ فسر معنى المتوسط في سياق الموقف. استعمل صيغ المتوسط والتباين والانحراف المعياري للتوزيع ذي الحدين في هذه التجربة ذات الحدين . n = 5, p = 0.35, 9 = 0.65 = np = 5 (0.35) = 1.75 02 = pa = 5 (0.35)(0.65) = 1.1375 σ = = √1.1375 1.0665 متوسط التوزيع يساوي 1.8 تقريبا، ويعني أن خريجين تقريبًا من أصل 5 أجابوا بنعم. كل من التباين والانحراف المعياري يساوي 1.1 تقريبا. تحقق من فهمك 3) كليات أوجد المتوسط والتباين والانحراف المعياري للمتغير العشوائي X في تحقق من فهمك 2 ، وفسّر معنى المتوسط في سياق الموقف. وزارة التعليم Ministry of Education 2024-1446

عندما يزداد عدد المحاولات في تجربة ذات الحدين يمكن استعمال التوزيع الطبيعي لتقريب التوزيع ذي الحدين. مفهوم أساسي تقريب التوزيع ذي الحدين إلى التوزيع الطبيعي في التوزيع ذي الحدين عندما تُمثَل " عدد المحاولات ، واحتمال النجاح P ، واحتمال الفشل و ، ويكون 25 ,5 n p، يمكن تقريب التوزيع ذي الحدين إلى توزيع طبيعي بمتوسط np = ، وانحراف معياري a = Vnpq . إرشادات للدراسة . التقريب إلى التوزيع الطبيعي مثال 4 تقريب التوزيع ذي الحدين إلى توزيع طبيعي أشارت دراسة سابقة إلى أن 64% من الخريجين يرون أن سنوات الجامعة كانت ممتعة. وقد نفذ بلال دراسة يستعمل التقريب إلى التوزيع مسحية على 300 من هؤلاء الخريجين اختارهم عشوائيا ما احتمال أن يوافق 200 خريج منهم على الأقل على ما الطبيعي: جاء في الدراسة الإحصائية السابقة؟ لأنه مع زيادة " يصبح استعمال التوزيع ذي الحدين لإيجاد الاحتمال عملية معقدة وصعبة. في الدراسة المسحية التي نفذها ،بلال، عدد الخريجين الذين يرون أن سنوات الجامعة كانت ممتعة يتبع التوزيع ذا الحدين، حيث وحيث إن: n = 300, p = 0.64, 9 = 0.36 n p = 300 (0.64) = 192 > 5 n q = 300 (0.36) = 108 5 يمكنك استعمال التوزيع الطبيعي لتقريب الاحتمال على النحو الآتي: np = المتوسط للتوزيع الطبيعي 11=300, p = 0.64 = 300(0.64)=192 Vnpa = الانحراف المعياري للتوزيع الطبيعي n=300, p = 0.64, q=0.36 = √300(0.64)(0.36) استعمل الآلة الحاسبة 8.31 13.5% 2% 0.5% 192 216 208 200 L 08 العدد 200 أكبر من المتوسط بمقدار انحراف معياري واحد تقريبا كما هو مبين في الرسم أعلاه؛ لذا يكون احتمال أن يوافق 200 خريج منهم على الأقل يساوي %16% تقريبا. تحقق من فهمك (4) أشارت دراسة سابقة إلى أن 32% من أولياء الأمور المستطلعة آراؤهم يرون أنه يجب تقليل عدد أيام الإجازة الصيفية للطلاب في نهاية العام الدراسي غير أن آية ترى أن النسبة أقل من ذلك، ولذلك قامت بإجراء دراسة مسحية شملت 250 من أولياء الأمور اختارتهم بطريقة عشوائية ممن استهدفتهم الدراسة السابقة. ما احتمال الايرى أكثر من 65 من أولياء الأمور وجوب تقليل عدد أيام الإجازة الصيفية؟ وزارة التعليم Ministry of Education الدرس 6-7 التوزيعات ذات الحدين 20756

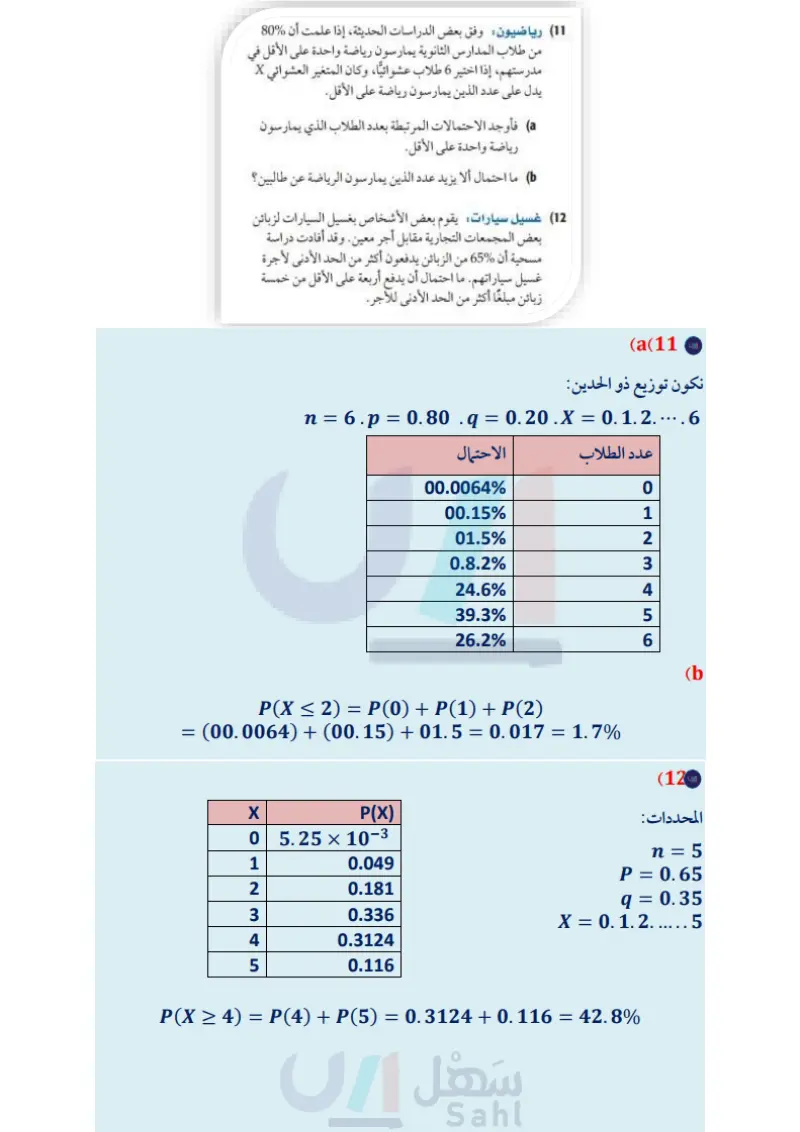
تدرب وحل المسائل حدد ما إذا كانت كل تجربة مما يأتي ذات حدين، أو يمكن جعلها ذات حدين. وإن كانت كذلك، فاكتب قيم ، ثم اكتب كل قيم المتغير العشوائي الممكنة، وإذا لم تكن تجربة ذات حدين فبين السبب (مثال (1) 9) رخصة قيادة اعتمادًا على إحدى الدراسات المسحية السابقة، إذا علمت أن 85% من طلاب إحدى الجامعات لديهم رخص قيادة سيارة، فما احتمال أن يكون 6 طلاب على الأقل من بين 10 تم اختيارهم عشوائيا لديهم رخص قيادة سيارة؟ (1) تم ترقيم أوجه مكعب بالأرقام من 1 إلى 6 ، ثم ألقي المكعب (10) كرة قدم: كسب فريق لكرة القدم %75.7 من مبارياته. أوجد 10 مرات، والمتغير العشوائي X يدل على عدد مرات ظهور الرقم 5 . احتمال أن يكسب 7 مباريات على الأقل من بين مبارياته العشر (2) ألقيت قطعة نقد 20 مرة، والمتغير العشوائي X يدل على عدد مرات ظهور الكتابة. (3) سألت 15 شخصا عن أعمارهم، والمتغير العشوائي X يدل على أعمار هؤلاء الأشخاص. (4) صندوق به 52 كرة، منها 13 كرة حمراء، و 13 كرة زرقاء، و13 كرة بيضاء، و13 كرة صفراء. سحبت 10 كرات على التوالي دون إرجاع. والمتغير العشوائي X يدل على عدد الكرات البيضاء المسحوبة. كون التوزيع ذا الحدين لكل متغير عشوائي مما يأتي، ومثله بالأعمدة، ثم أوجد المتوسط، وفسّر معناه في سياق الموقف، ثم أوجد التباين والانحراف المعياري (المثالان (23) (5) إذا كان 89% من طلاب المرحلة الثانوية في إحدى المدارس. القادمة. 11 رياضيون وفق بعض الدراسات الحديثة، إذا علمت أن %80 من طلاب المدارس الثانوية يمارسون رياضة واحدة على الأقل في مدرستهم، إذا اختير 6 طلاب عشوائيا، وكان المتغير العشوائي X يدل على عدد الذين يمارسون رياضة على الأقل. فأوجد الاحتمالات المرتبطة بعدد الطلاب الذي يمارسون رياضة واحدة على الأقل. ما احتمال ألا يزيد عدد الذين يمارسون الرياضة عن طالبين؟ (12) غسيل سيارات يقوم بعض الأشخاص بغسيل السيارات لزبائن بعض المجمعات التجارية مقابل أجر معين. وقد أفادت دراسة مسحية أن 65% من الزبائن يدفعون أكثر من الحد الأدنى لأجرة غسيل سياراتهم. ما احتمال أن يدفع أربعة على الأقل من خمسة يتابعون مباريات منتخبهم الوطني، وتم اختيار 5 طلاب عشوائياً من هذه المدرسة، وسؤالهم عما إذا كانوا يتابعون مباريات منتخبهم الوطني. 6 بينت دراسة أن % 26% من موظفي إحدى الشركات يستعملون الإنترنت في عملهم. إذا تم اختيار 10 موظفين من هذه الشركة عشوائيا، وسؤالهم عما إذا كانوا يستعملون الإنترنت في عملهم. (7) أفادت دراسة إحصائية أن %65% من طلاب الجامعات الذين يمتلكون سيارات يستعملون أحزمة الأمان في أثناء قيادة سياراتهم. إذا تم اختيار 8 طلاب عشوائياً ممن يمتلكون سيارات، وسؤالهم إن كانوا يستعملون أحزمة أمان في أثناء قيادة سياراتهم. 8 أعمال صيفية : تبين في دراسة سابقة أن 90%. من طلاب زبائن مبلغا أكثر من الحد الأدنى للأجر. (13) حوافز دعائية : تضع شركة للعصائر حوافز بحيث إن %30 من علب العصير تربح علبة مجانية، وقد اشترت سعاد 10 علب. مثل بالأعمدة البيانية التوزيع الاحتمالي للتوزيع ذي الحدين إذا كان المتغير العشوائي يدل على عدد علب العصير الرابحة. (14) برامج دينية: بناءً على دراسة مسحية سابقة، إذا علمت أن %70 من الأشخاص تحت سن العشرين يتابعون برنامجا دينيا على الأقل في التلفاز. إذا استطلع خليل رأي 200 شخص تحت سن 20 سنة، فما احتمال أن 146 شخصًا منهم على الأقل يتابعون برنامجا دينيا على الأقل؟ الصفوف العليا في مدرسة ثانوية يحصلون على أعمال صيفية، لكن إذا علمت أن نسبة النجاح في توزيع ذي حدين %60، ويوجد 18 محاولة، منذرًا قدر أن النسبة أقل من ذلك؛ لذا قام بدراسة مسحية شملت فأجب. 400 طالب من الصفوف العليا تم اختيارهم عشوائيا ما احتمال ألا يكون أكثر من 348 من الطلاب المستهدفين حصلوا على عمل (15) ما احتمال ألا توجد أي محاولة ناجحة؟ (16) ما احتمال أن توجد 12 محاولة فاشلة؟ صيفي ؟ (مثال (4) 76 الفصل 7 الاحتمال والإحصاء وزارة التعليم Ministry of Education 2024-1446

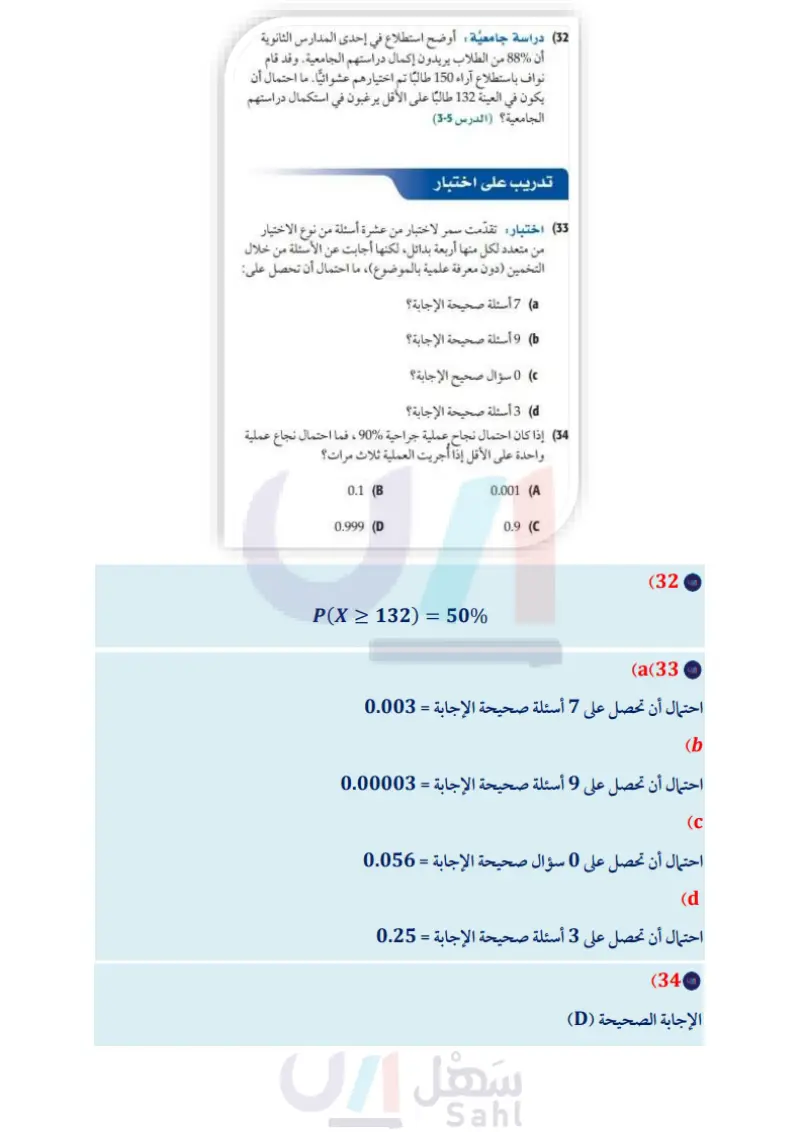
(17) تنس طاولة كسب لاعب 85% من مبارياته التي لعبها خلال مسيرته الرياضية، أوجد الاحتمالات الآتية: a أن يكسب 3 مباريات من بين 5 مباريات قادمة. أن يكسب مبارتين على الأقل من بين المباريات الخمس القادمة. أن يخسر مباراة واحدة على الأقل في مبارياته الخمس القادمة. لكل من التوزيعات ذات الحدين الآتية، يدل الرمز " على عدد مراجعة تراكمية حدد ما إذا كانت المعادلة في كل ممايأتي تمثل دائرة، أو قطعا مكافتًا، أو قطعاً ناقصا أو قطعًا ،زائدا دون كتابتها على الصورة القياسية. وبرر إجابتك (مهارة سابقة) x2 + 4y2 = 100 (28) 5y2-10x=0 (29 x2 + y2 - 3x + 4y - 16 = 0 (30 المحاولات، ويدل الرمز p على احتمال نجاح كل محاولة. أوجد احتمال 31) سرعة وضع نظام لمراقبة سرعة السيارات وتسجيلها في شارع الحصول على X من النجاحات. n = 8, p = 0.3, X 2 2 18 n = 10, p = 0.2, X>2 (19 n = 6, p = 0.6, X 5 4 20 n = 9, p = 0.25, X 5 (21 n = 10, p = 0.75, X≥8 (22 قريب من إحدى المدارس إذا توزّعت هذه السرعات توزيعا طبيعيا بمتوسط 37mi/h ، وانحراف معياري 4mih، فكم سيارة كانت تسير بسرعة تقل عن 33mi/h في عينة حجمها 425 سيارة؟ (الدرس 5-7) (32) دراسة جامعية : أوضح استطلاع في إحدى المدارس الثانوية أن 88% من الطلاب يريدون إكمال دراستهم الجامعية. وقد قام نواف باستطلاع آراء 150 طالبًا تم اختيارهم عشوائياً. ما احتمال أن يكون في العينة 132 طالبًا على الأقل يرغبون في استكمال دراستهم الجامعية؟ (الدرس 5-7) n = 12, p = 0.1, X <3 (23 مسائل مهارات التفكير العليا (24) تحد في تقريب التوزيع ذي الحدين إلى التوزيع الطبيعي، إذا علمت أن احتمال وجود 66 - 60 نجاحًا يساوي %34، وكان 60 = ، واحتمال النجاح 36 ، فكم كان عدد المحاولات؟ (25) تبرير حدد ما إذا كانت العبارة الآتية صحيحة دائمًا، أو صحيحة أحيانًا، أو غير صحيحة أبدًا. وبرّر إجابتك. ( من الأفضل أن تجد احتمال الفشل وتطرحه من 1 لتجد احتمال النجاح . (26) مسألة مفتوحة صف حالة من أنشطة المدرسة أو المجتمع ينطبق عليها التوزيع ذو الحدين، وحدّد عدد المحاولات المستقلة (n) ، وكلا من احتمال النجاح و احتمال الفشل في المحاولة الواحدة. (27) اكتب فسّر العلاقة بين التجربة ذات الحدين والتوزيع ذي الحدين. تدريب على اختبار (33) اختبار: تقدمت سمر لاختبار من عشرة أسئلة من نوع الاختيار من متعدد لكل منها أربعة بدائل لكنها أجابت عن الأسئلة من خلال التخمين (دون معرفة علمية بالموضوع)، ما احتمال أن تحصل على: 7 أسئلة صحيحة الإجابة؟ ) وأسئلة صحيحة الإجابة؟ سؤال صحيح الإجابة؟ 3 أسئلة صحيحة الإجابة؟ (34) إذا كان احتمال نجاح عملية جراحية 90% ، فما احتمال نجاع عملية واحدة على الأقل إذا أجريت العملية ثلاث مرات؟ 0.1 (B 0.999 (D 0.001 (A 0.9 (C وزارة التعليم Ministry of Education الدرس 6-7 التوزيعات ذات الحدين 207716

الفصل 7 78 دليل الدراسة والمراجعة ملخص الفصل مفاهيم أساسية العينة والمجتمع الدرسان -1- • تكون العينة متحيزة إذا صُممت لصالح نواتج معينة . . تكون العينة غير متحيزة إذا كانت عشوائية. الارتباط والسببية المفردات الدراسة المسحية ص 44 المجتمع ص 44 تعداد عام ص 44 العينة ص 44 المتحيزة ص 44 غير المتحيزة ص 44 الدراسة القائمة على . عندما يوجد ارتباط بين ظاهرتين فإن كلا منهما تؤثر في الملاحظة ص 45 الأخرى، وعندما يوجد سببية، فإن وقوع ظاهرة معينة يكون الدراسة التجريبية ص 45 سببا مباشرًا في وقوع الظاهرة الأخرى. هامش خطأ المعاينة المجموعة التجريبية ص 45 المجموعة الضابطة ص 45 عند سحب عينة حجمها 7 من مجتمع، فإنه يمكن تقريب هامش خطأ المعاينة بالقيمة: الارتباط ص 46 السببية ص 46 . المجتمع 1 √π الانحراف المعياري العينة Σ(x-2)² k= 12 2 - 1)2 11-1 الاحتمال المشروط (الدرس (73) . الاحتمال المشروط : هو احتمال وقوع حادثة معينة إذا علم وقوع حادثة أخرى. . الجداول التوافقية : هي جداول تكرارية ذات بعدين يتم فيها تسجيل بيانات ضمن خلايا، حيث إن كل خلية من خلايا الجدول تُمثل تكرارًا يسمى تكرارًا نسبيا، إذ يكون منسوبا إلى مجموع التكرارات في الجدول، أو منسوبا إلى مجموع التكرارات في الصف الذي تقع فيه الخلية، أو منسوبا إلى مجموع التكرارات في العمود الذي تقع فيه الخلية، ويمكن استعمال الجداول التوافقية في إيجاد الاحتمال المشروط . التوزيعات الاحتمالية ( الدروس 6-5-4-17 التحليل الإحصائي ص 50 المتغير ص 50 بيانات في متغير واحد ص 50 مقياس النزعة المركزية ص 50 المعلمة ص 50 الإحصائي ص 50 هامش خطأ المعاينة ص 51 الانحراف المعياري ص 51 الاحتمال المشروط ص 55 الجدول التوافقي ص 56 التكرار النسبي ص 56 60 النجاح صا الفشل ص 60 المتغير العشوائي ص 61 المتغير العشوائي المنفصل ص 61 التوزيع الاحتمالي ص 61 التوزيع الاحتمالي المنفصل ص 61 الاحتمال النظري ص 62 الاحتمال التجريبي ص 62 66 القيمة المتوقعة ص 62 التوزيع الاحتمالي المتصل ص التوزيع الطبيعي ص 66 التوزيع الملتوي ص 66 تجربة ذات حدين ص 72 التوزيع ذو الحدين ص 73 مقاييس التشتت ص 51 التباين ص 51 اختبر مفرداتك اختر المفردة المناسبة لكل عبارة مما يأتي من القائمة أعلاه: (1 المتغير عشوائي معين هو دالة تربط فضاء العينة باحتمالات نواتج فضاء العينة . (2) عندما توجد علاقة بين حادثتين، فإنه يوجد بينهما. (3) الدراسة المسحية تكون. نواتج معينة. إذا صممت لصالح (4) إذا أعطيت مجموعة معالجة شكلية لا أثر لها في النتيجة، فإن هذه المفهوم منفصل الوصف المجموعة تسعى. عدد محدد من النواتج الممكنة (5) يُحدّد . الفترة التي تبين الفرق في الاستجابة متصل عدد غير محدد من النواتج الممكنة طبيعي بين العينة والمجتمع . منحنيات متماثلة ملتوي منحنيات غير متماثلة تجربة ذات الحدين تجربة احتمالية يكون لها نتيجتان فقط الفصل 7 الاحتمال والإحصاء وزارة التعليم Ministry of Education 2024-1446

الفصل 7 دليل الدراسة والمراجعة 7-1 الدراسات التجريبية والمسحية والقائمة على الملاحظة ( الصفحات 44 - 48 ) حدد ما إذا كانت كل دراسة مسحية فيما يأتي تتبني عينة متحيزة أو غير متحيزة، ثم فسّر إجابتك: مثال 1 اختار صاحب وكالة للسيارات 100 زبون عشوائيا قاموا بإجراء الصيانة الدورية لسياراتهم في الوكالة حديثا، وطرح سؤالا عليهم حول نوعية يتم اختيار كل عاشر متسوّق يخرج من مجمع تجاري؛ لمعرفة إن الخدمة التي تُقدّمها الوكالة. هل يُمثل الزبائن الذين تم اختيارهم عينة كان مرتاحا أو مطمئنا لشرائه من المجمع. (7) يتم اختيار كل عاشر طالب يخرج من المدرسة؛ لمعرفة أحب غير متحيزة ؛ لأنّ لكل شخص من زبائن الوكالة الفرصة نفسها لأن المواد الدراسية إليه في المدرسة. يطلب أحد مطاعم الوجبات السريعة إلى زبائنه أن يكملوا استبانة حول أفضل مطعم للوجبات السريعة. متحيزة أم غير متحيزة؟ فسّر إجابتك. يكون من بين العينة. مثال 2 وزع معلم الرياضيات طلابه مجموعتين عشوائيا، وطبق عليهم اختبارًا، حدد ما إذا كانت كل حالة تحتاج إلى دراسة مسحية أو دراسة قائمة على حيث طلب من المجموعة الأولى أداء تمارين رياضية قبل الاختبار، الملاحظة أو دراسة تجريبية. بينما أعطى المجموعة الثانية الاختبار دون أن يطلب منهم تأدية أي (9) اختر 100 طالب نصفهم يعمل جزئيا بعد الدراسة، وقارن بين تمارين رياضية، وقارن نتائجهم في الاختبار. هل هذه الدراسة دراسة مسحية أم دراسة قائمة على الملاحظة أم دراسة تجريبية؟ وإذا كانت الأوساط لدرجاتهم. 10) اختر 100 شخص، وقسمهم إلى نصفين عشوائيا، ودع إحدى تجريبية، فاذكر كلا من المجموعتين الضابطة والتجريبية، ثم بين ما إذا المجموعتين تتناول وجبات قليلة الدسم، بينما تتناول الأخرى كانت الدراسة متحيزة أم لا. وجبات اعتيادية. وقارن النتائج؛ لمعرفة أثر الوجبات القليلة دراسة تجريبية: المجموعة التجريبية هي الأولى، والضابطة هي الثانية، والدراسة التجريبية متحيزة؛ لأن كل طالب يعرف المجموعة التي الدسم على صحة الجسم. 7-2 ينتمي اليها. التحليل الإحصائي ( الصفحات 50 - 54 ) (11) فصول السنة : في دراسة مسحية عشوائية شملت 3446 مثال 3 شخصا، ذكر %34% منهم أن الربيع هو أفضل فصول السنة لديهم. قال %12% من عينة حجمها 2645 شخصا : إن كرة القدم هي الأكثر ما هامش الخطأ في المعاينة؟ 12) سباحة في أثناء تمرين السباحة، قاس خالد الأزمنة التي استغرقها في كل مرة لقطع مسافة 400m ، وسجل النتائج الممثلة في الجدول أدناه أوجد الانحراف المعياري للأزمنة التي حققها. تفضيلا لديهم. ما هامش خطأ المعاينة ؟ 2645 0.019 ±= هامش خطأ المعاينة =± الزمن بالثواني 307 312 308 320 311 301 302 304 308 309 315 313 306 314 316 313 313 311 309 306 310 319 326 329 309 314 318 315 318 320 هامش خطأ المعاينة %1.9 تقريبا. وزارة التعليم Ministry of Education الفصل 7 دليل الدراسة والمراجعة 20796

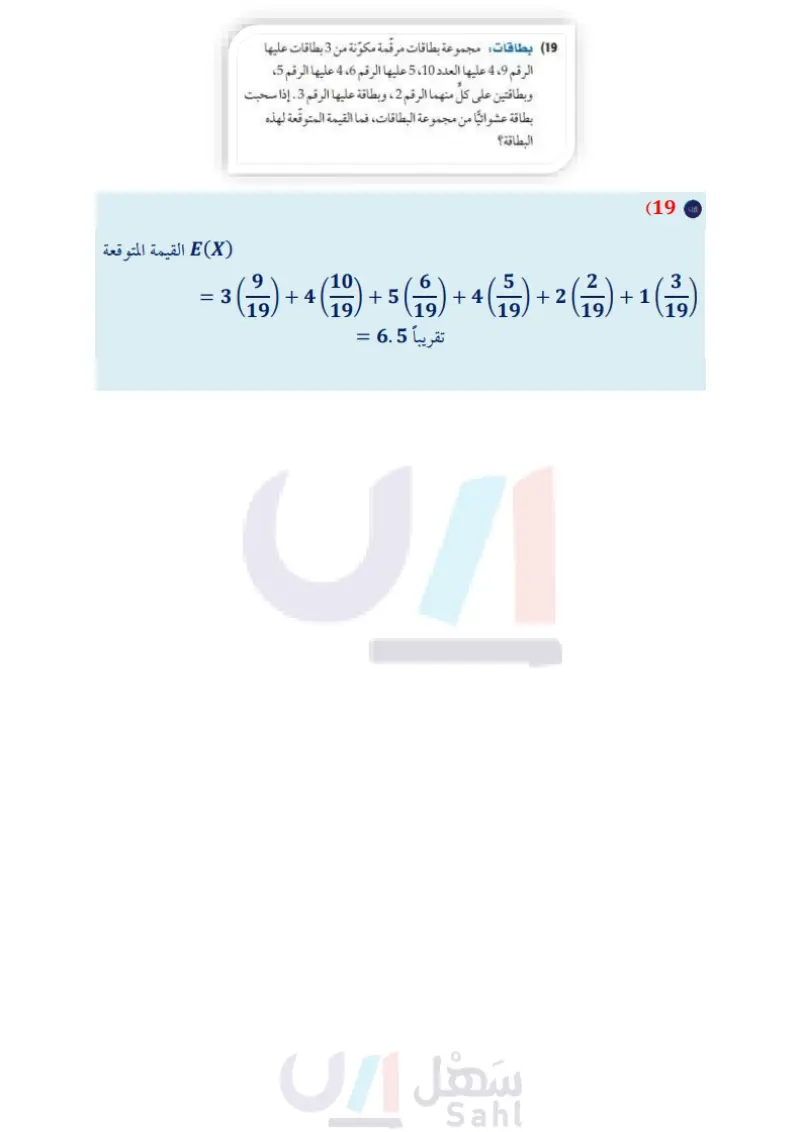
الفصل 7 80 7-3 دليل الدراسة والمراجعة ا الاحتمال المشروط ( الصفحات 55 - 58) (13) كرة طائرة يحصل طارق على نقطة في %65% من مرات مثال 4 قيامه بضربة الإرسال ما احتمال ألا يحصل على نقطة في ضربة دراسة: أوجد احتمال أن يأخذ طالب اختير عشوائيا حصة إضافية الإرسال الثانية علمًا بأنه حصل على نقطة في ضربة الإرسال الأولى؟ 14) في الجدول أدناه إذا اختير طالب عشوائيا فأجب عما يأتي: يلبس نظارات لا يلبس نظارات علما بأنه طالب جديد. يأخذ حصصا إضافية (E) لا يأخذ حصصا إضافية (X) طالب جديد (N) طالب قديم (0) 126 98 84 72 7-4 الأول الثانوي الثاني الثانوي 6 5 15 22 ما احتمال أن يكون الطالب من الأول الثانوي علما بأنه يلبس نظارات؟ ما احتمال أن يكون من الذين لا يلبسون النظارات علما بأنه من الثاني الثانوي؟ P(E|N)= P(EN) P(N) 126 210 ÷ 380 380 126 210 الاحتمال والتوزيعات الاحتمالية ( الصفحات 60 - 65 ) مثال 5 قانون الاحتمال المشروط P(ENN) = 126 380 ,P(N)= 210 380 بسط قرعة الألعاب : خلط يوسف بطاقات الألعاب جميعها في صندوق، حيث تشكلت البطاقات من 12 بطاقة لكرة القدم، 8 بطاقات لدى حمزة 5 كتب في حقيبته، هي الرياضيات والكيمياء واللغة لكرة الطائرة، 5 بطاقات لكرة السلة وجميعها متماثلة. إذا تم اختيار 3 الإنجليزية واللغة العربية والتاريخ. إذا قام بترتيبها على رف في صف واحد عشوائيا، فما احتمال أن تأتي كتب اللغة الإنجليزية واللغة العربية بطاقات بصورة عشوائية، فأوجد احتمال كل من: (15) (3 بطاقات للكرة الطائرة)P 16) (3) بطاقات لكرة القدم) P (17) (بطاقة لكرة السلة وبطاقتان للكرة الطائرة)P 18) (بطاقتان لكرة السلة وبطاقة لكرة القدم)P (19) بطاقات مجموعة بطاقات مرقمة مكونة من 3 بطاقات عليها الرقم 9، 4 عليها العدد 10، 5 عليها الرقم 6، 4 عليها الرقم 5، وبطاقتين على كل منهما الرقم 2 ، وبطاقة عليها الرقم 3. إذا سحبت بطاقة عشوائيا من مجموعة البطاقات، فما القيمة المتوقعة لهذه البطاقة؟ والرياضيات في أقصى اليسار ؟ الخطوة 1 حدد عدد النجاحات. 3P3 2P2 مكان الكتب الثلاثة إلى اليسار أمكنة الكتابين الآخرين استعمل التباديل ومبدأ العد الأساسي لإيجاد ؟ . S3P3 2P2 3!.2! = 12 الخطوة 2 أوجد عدد عناصر فضاء العينة s + f. = 5! 5P5 = 120 s + f = 120 وتمثل عدد الترتيبات الممكنة للكتب الخمسة على الرف. الخطوة 3 أوجد الاحتمال P(S): == s+ 12 = 0.1 120 احتمال النجاح احتمال وضع كتب اللغة الإنجليزية واللغة العربية والرياضيات في أقصى اليسار يساوي 0.1 أو %10. وتلي التعليم الفصل 7 الاحتمال والإحصاء Ministry of Education 2024-1446

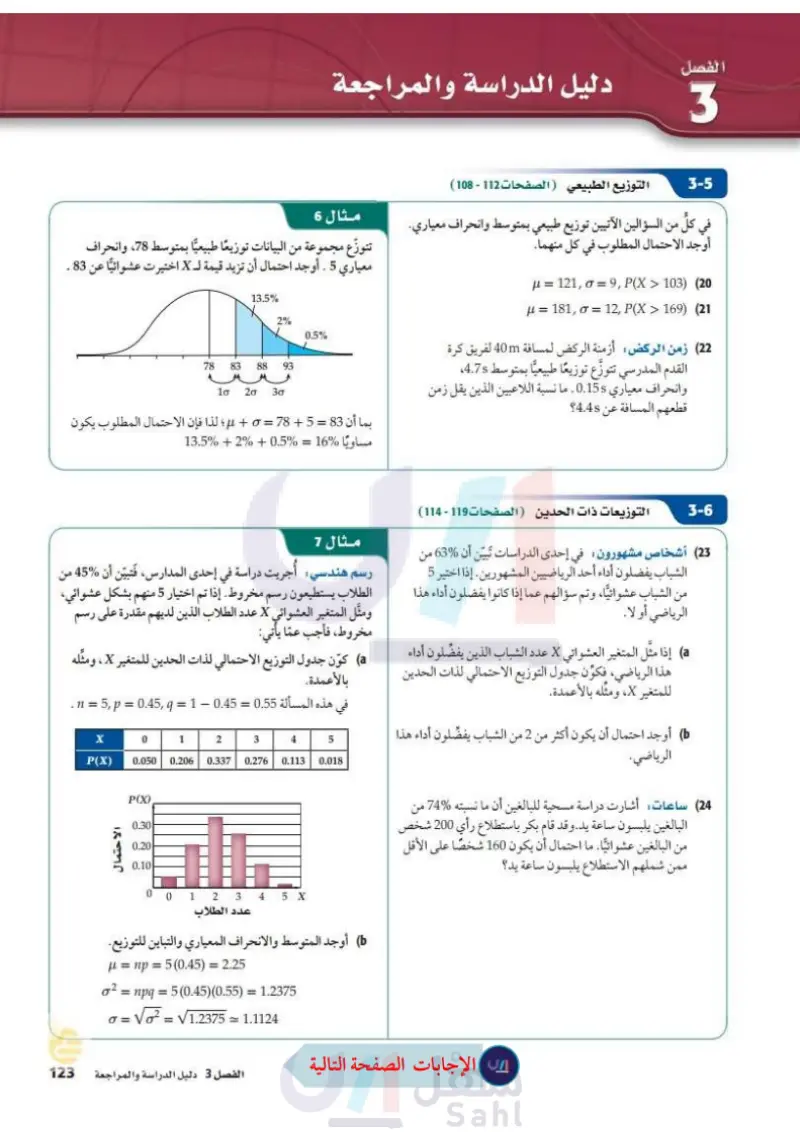
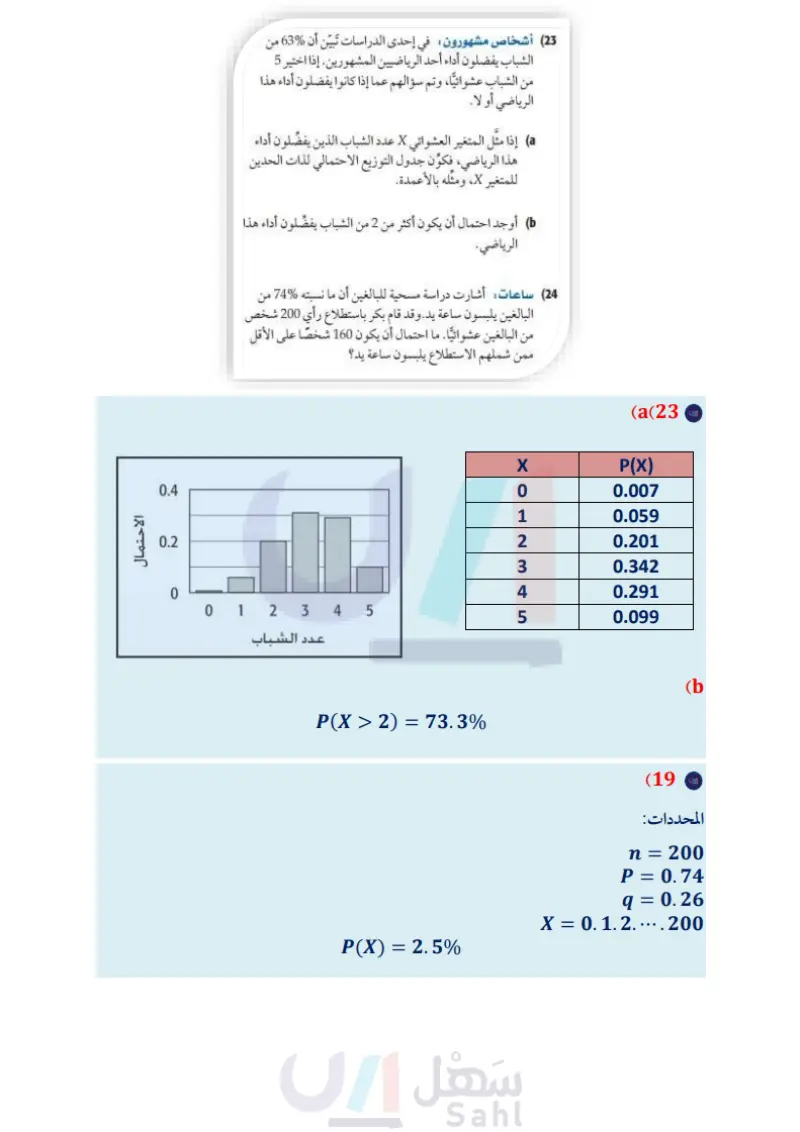
الفصل 7 دليل الدراسة والمراجعة 7-5 التوزيع الطبيعي ( الصفحات 66 - 70) مثال 6 في كلُّ من السؤالين الآتيين توزيع طبيعي بمتوسط وانحراف معياري. أوجد الاحتمال المطلوب في كل منهما. تتوزع مجموعة من البيانات توزيعاً طبيعياً بمتوسط 78، وانحراف معياري 5. أوجد احتمال أن تزيد قيمة لـ X اختيرت عشوائيا عن 83 . . 121, σ 9, P(X > 103) (20 F = 181, 0 = 12, P (X > 169) (21) (22) زمن الركض أزمنة الركض لمسافة 40m لفريق كرة القدم المدرسي تتوزع توزيعا طبيعيا بمتوسط 4.78 وانحراف معياري 0.155. ما نسبة اللاعبين الذين يقل زمن قطعهم المسافة عن 4.48 7-6 0.5% 13.5% 2% 83 88 78 93 30 20 10 بما أن 83 = 5 + 78 = o + ؛ لذا فإن الاحتمال المطلوب يكون مساويًا 16 = %0.5 + %2 + %13.5 التوزيعات ذات الحدين ( الصفحات 72 - 77 ) مثال 7 (23) أشخاص مشهورون في إحدى الدراسات تبين أن %63% من الشباب يفضلون أداء أحد الرياضيين المشهورين. إذا اختير 5 رسم هندسي: أُجريت دراسة في إحدى المدارس، فتبين أن %45 من من الشباب عشوائيا، وتم سؤالهم عما إذا كانوا يفضلون أداء هذا الطلاب يستطيعون رسم مخروط . إذا تم اختيار 5 منهم بشكل عشوائي، ومثل المتغير العشوائي X عدد الطلاب الذين لديهم مقدرة على رسم مخروط، فأجب عما يأتي: الرياضي أو لا. a إذا مثل المتغير العشوائي X عدد الشباب الذين يفضّلون أداء هذا الرياضي، فكون جدول التوزيع الاحتمالي لذات الحدين للمتغير x ، ومثله بالأعمدة. أوجد احتمال أن يكون أكثر من 2 من الشباب يفضّلون أداء هذا الرياضي 24 ساعات أشارت دراسة مسحية للبالغين أن ما نسبته %74% من البالغين يلبسون ساعة يد. وقد قام بكر باستطلاع رأي 200 شخص من البالغين عشوائيا. ما احتمال أن يكون 160 شخصا على الأقل ممن شملهم الاستطلاع يلبسون ساعة يد؟ ) كوّن جدول التوزيع الاحتمالي لذات الحدين للمتغير x ، ومثله بالأعمدة. في هذه المسألة 0.55 = 0.45 - 1 = n = 5, p = 0.45, q . X 0 1 2 3 4 5 P(X) 0.113 0.276 0.337 0.206 0.050 0.018 P(X) 0.30 0.20 0.10 0 0 1 2 3 4 5 X عدد الطلاب أوجد المتوسط والانحراف المعياري والتباين للتوزيع. H = np = 5(0.45) = 2.25 02 = npg = 5 (0.45) (0.55) = 1.2375 =√1.2375 1.1124 وزارة التعليم Ministry of Education الفصل 7 دليل الدراسة والمراجعة 20816

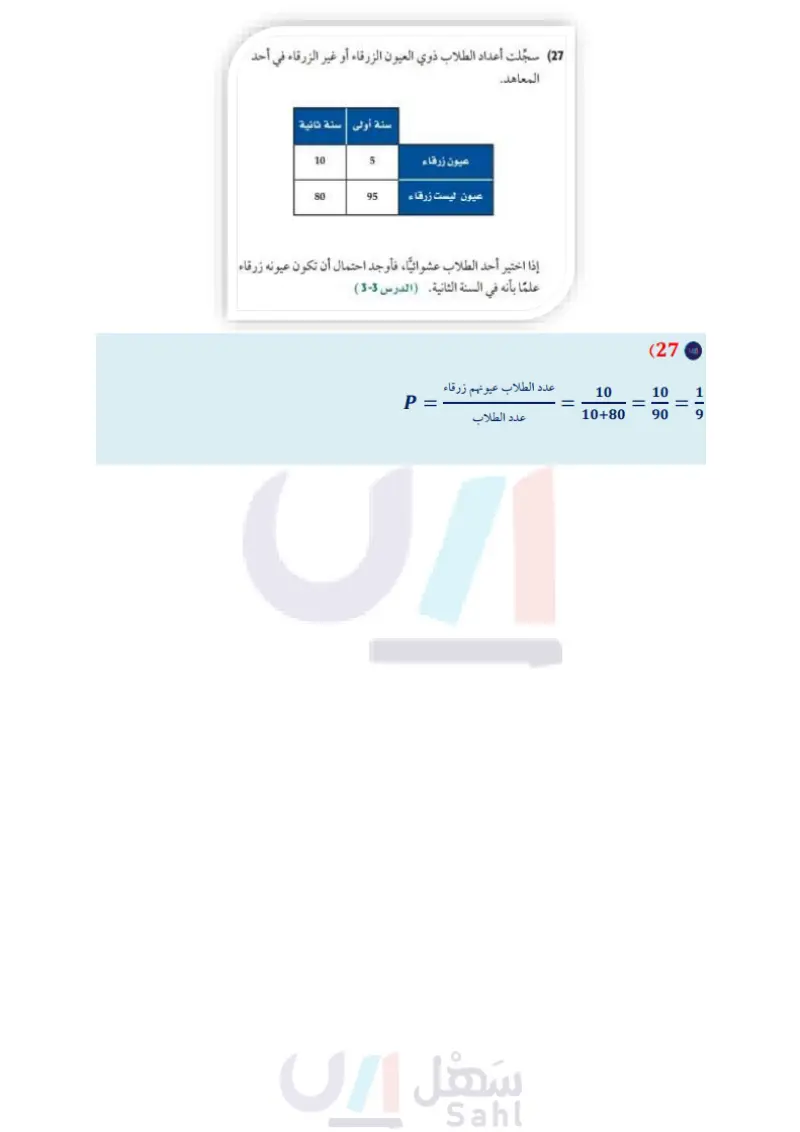
الفصل 7 دليل الدراسة والمراجعة تطبيقات ومسائل لا حدد ما إذا كان كل موقف مما يلي يمثل دراسة تجريبية، أو دراسة (28) رميت 3 قطع نقد مرة واحدة. إذا كان المتغير العشوائي X يدل على عدد مرات ظهور الشعار فاكتب جدول التوزيع الاحتمالي للمتغير قائمة على الملاحظة، وفي حالة الدراسة التجريبية، اذكر كلا من المجموعة الضابطة والمجموعة التجريبية، ثم بين إن وجد تحيز أو لا: (الدرس 1-7) اختر 100 طالب نصفهم يأتي إلى المدرسة مبكرًا، وقارن بين تحصيلهم في مادة معينة. اختر 100 موظف، واقسمهم نصفين، وأخضع إحدى المجموعتين إلى دورة في اللغة الإنجليزية، أما الأخرى فلا تخضعها لأي دورة تدريبية. (26) اختير 10 طلاب بصورة عشوائية من الصف الثالث الثانوي، وقيست أطوالهم بالسنتمترات فكانت كما يلي: العشوائي X ، ثم مثله بالأعمدة. (الدرس 4-7) (29) سكة حديد إذا كانت الفترات الزمنية للانتظار التي يقضيها 16000 مسافر في إحدى محطات سكك الحديد موزعة توزيعا طبيعيًا بمتوسط 72min ، وانحراف معياري 15min، فأوجد نسبة المسافرين الذين ينتظرون أكثر من 42min الدرس 5-7 ) (30) إجازات في دراسة مسحية سابقة وجد أن ما نسبته %70 من العاملين يأخذون إجازاتهم السنوية في الصيف، لكن محسناً يعتقد أن هذا الرقم مبالغ فيه، فقام باستطلاع رأي 650 عاملًا عشوائيا. ما احتمال ألا يأخذ أكثر من 420 عاملًا إجازاتهم في الصيف؟ الدرس 6-7) 170, 165, 155, 168, 177, 180, 168, 167, 160, 161 بين ما إذا كانت هذه البيانات تمثل عينة أم مجتمعاً، ثم أوجد الانحراف المعياري لهذه الأطوال (الدرس 2-7) (27) سجلت أعداد الطلاب ذوي العيون الزرقاء أو غير الزرقاء في أحد 82 المعاهد. سنة أولى | سنة ثانية عيون زرقاء 10 5 عيون ليست زرقاء 80 95 إذا اختير أحد الطلاب عشوائيا، فأوجد احتمال أن تكون عيونه زرقاء علما بأنه في السنة الثانية (الدرس 3-7) الفصل 7 الاحتمال والإحصاء وزارة التعليم Ministry of Education 2024-1446

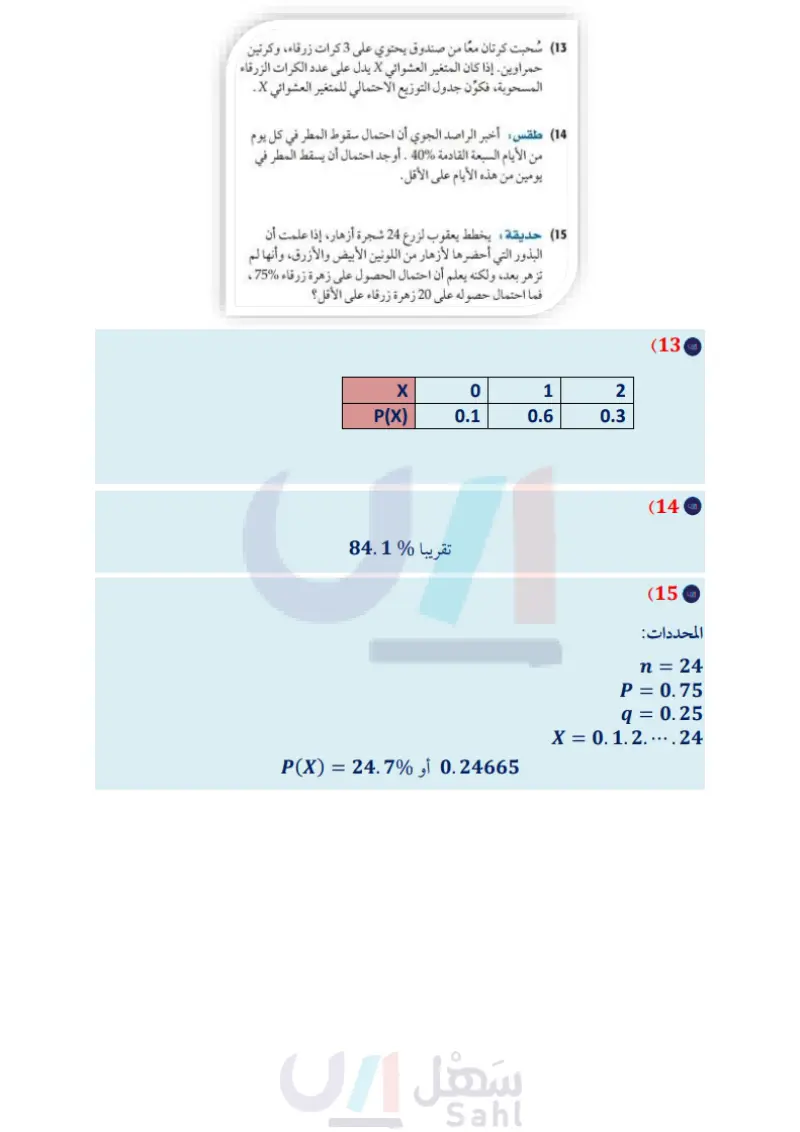
الفصل 7 اختبار الفصل حدد ما إذا كانت العبارات الآتية تصف ارتباطا أو سببية، ثم فسّر إجابتك: 11) اختبارات أعطى المعلم أيمن طلابه الفرصة لإعادة أحد 1) عندما يرى محمود البرق، فإنه يسمع الرعد بعد ذلك. (2) عندما يركض نايف عند مدخل المدرسة، فإنه يكون متأخرا عن المدرسة. حدد ما إذا كانت كل دراسة مسحية فيما يأتي تتبنى عينة متحيزة أو غير متحيزة، ثم فسّر إجابتك: (3) استطلع صاحب مخزن يبيع من خلال الشبكة العنكبوتية زبائنه عن أهمية وجود الإنترنت في المنزل. (4) يختار معلم 5 أسماء لطلاب يدرسهم؛ لإلقاء كلمة الصباح بعد أن يقوم بوضع الأسماء جميعها في سلة ويخلطها . أي مقاييس النزعة المركزية يصف كلا من البيانات الآتية بصورة أفضل؟ ولماذا ؟ درجات اختبار (5) 3 3 3 4 4 4 4 5 5 4 4 3 3 3 3 4 4 3 3 3 الاختبارات، كما عقد درس مراجعة اختياري يوم الخميس قبل إعادة الاختبار لمن يرغب بعض الطلاب تحسن أداؤهم، والبعض الآخر لم يتحسن، والجدول أدناه يبين ذلك. إذا اختير طالب عشوائيا، فأوجد: حضر المراجعة لم يحضر المراجعة تحسن لم يتحسن 3 12 6 4 a احتمال أن يكون قد تحسّن علما بأنه حضر المراجعة. احتمال أنه لم يحضر المراجعة علما بأنه لم يتحسن. (12) اختيار من متعدد شارك 10 طلاب من الصف الأول الثانوي و 12 طالبًا من الصف الثاني الثانوي في السحب على 5 جوائز. إذا كان السحب عشوائياً، فما احتمال أن يكون الرابحون 3 من الصف الأول الثانوي، وطالبين من الصف الثاني الثانوي؟ A 0.46% تقريبا 3 4 3 5 4 B 0.25% تقريباً الطول بالبوصة (6 64 61 62 64 61 83 66 61 65 63 61 65 62 63 84 61 63 62 66 61 فيما يأتي المتوسط والانحراف المعياري لمجموعة من البيانات تتوزع توزيعا طبيعيا، أوجد الاحتمال المطلوب في كل منها : μ=54,σ = 5, P(X > 44) (7 μ=35, σ = 2.4, P(X < 37.4) (8 يحتوي كيس على 10 كرات زجاجية زرقاء، و8 كرات حمراء، 70% تقريبا 30%D تقريبا (13) سُحبت كرتان معًا من صندوق يحتوي على 3 كرات زرقاء، وكرتين حمراوين. إذا كان المتغير العشوائي X يدل على عدد الكرات الزرقاء المسحوبة، فكون جدول التوزيع الاحتمالي للمتغير العشوائي X . 14 طقس أخبر الراصد الجوي أن احتمال سقوط المطر في كل يوم من الأيام السبعة القادمة %40 . أوجد احتمال أن يسقط المطر في يومين من هذه الأيام على الأقل. 15) حديقة يخطط يعقوب لزرع 24 شجرة أزهار، إذا علمت أن و 12 خضراء، وجميعها متماثلة، سحبت كرتان واحدة تلو الأخرى، أوجد البذور التي أحضرها لأزهار من اللونين الأبيض والأزرق، وأنها لم الاحتمال لكل من : (9) الكرة الثانية حمراء، علما بأن الكرة الأولى زرقاء دون إرجاع. (10) الكرة الثانية زرقاء، علما بأن الكرة الأولى خضراء مع الإرجاع. تزهر بعد، ولكنه يعلم أن احتمال الحصول على زهرة زرقاء %75 ، فما احتمال حصوله على 20 زهرة زرقاء على الأقل؟ وزارة التعليم Ministry of Education الفصل 7 اختبار الفصل 20836