المثلثات المتشابهة - رياضيات 1-3 - أول ثانوي

المثلثات المتشابهة Similar Triangles 6-2 فيما سبق لماذا؟ أراد خالد أن يرسم نسخة مشابهة لشعار نادي التزلج المجاور على مُلصق بر، فبدأ أولا برسم قطعة مستقيمة أسفل الملصق، ثم استعمل نسخة من المثلث الأصلي لينسخ زاويتي القاعدة، ثم مد الضلعين غير المشتركين درست استعمال المسلمتين كبير، SAS والنظرية AAS لإثبات تطابق مثلثين. (مهارة سابقة ) والان : . أحدد المثلثات المتشابهة باستعمال مسلمة التشابه AA ونظريتي التشابه SSS, SAS . أستعمل المثلثات المتشابهة لحل المسائل. للزاويتين. www.ien.edu.sa نادي التزلج تحديد المثلثات المتشابهة: في الفصل الثالث تعلمت اختبارات تحديد ما إذا كان مثلثان متطابقين أم لا، ولتشابه المثلثات اختبارات أيضًا. والرسم السابق يبين أنه إذا طابقت زاويتان في مثلث زاويتين في مثلث آخر، فإن المثلثين متشابهان. مسلمة 6.1 التشابه بزاويتين (AA) إذا طابقت زاويتان في مثلث زاويتين في مثلث آخر فإن المثلثين متشابهان F مثال في المثلثين ABC ، إذا كانت A = F, B = LG ، أضف إلى مطويتك A B H فإن AABC - AFGH. مثال 1 استعمال مسلمة التشابه DD حدد في كل مما يأتي ما إذا كان المثلثان متشابهين أم لا ؟ وإذا كانا كذلك، فاكتب عبارة التشابه. R (6 T S W L 48° 57' K ووضح إجابتك. M P (e 57° 75 بما أن: ML = mM، إذن : L = M ومن نظرية مجموع قياسات زوايا المثلث يكون 180° = mZK + 48° + 57 ؛ إذن °75 = mK. وبما أنّ 75 = mP ، فإن K = P ؛ إذن ALJK - MQP وفق المسلمة AA. ) RSX = WST وفق نظرية الزاويتين المتقابلتين بالرأس. ولأن RX || TW ، فإن CR = W وفق نظرية الزاويتين المتبادلتين داخليا؛ إذن ARSX - AWST وفق المسلمة AA. تحقق من فهمك : حدد في كل مما يأتي ما إذا كان المثلثان متشابهين أم لا؟ وإذا كانا كذلك ، فاكتب عبارة وزارة التعليم Ministry of Education 2024-1446 L PA K (18) التشابه ووضح إجابتك. (10) A D F 472 44" C B G الفصل 6 التشابه 20

أضف إلى مطويتك A L R B S X C M K Y G P إرشادات للدراسة يمكنك استعمال مسلمة التشابه AA لإثبات النظريتين الآتيتين: رسم الأشكال : قد تساعدك إعادة رسم المثلثين المتشابهين بحيث تظهر الأضلاع المتناظرة في الاتجاه نظريتان 6.2 التشابه بثلاثة أضلاع (SSS) إذا كانت أطوال الأضلاع المتناظرة لمثلثين متناسبة، فإن ، فإن JK MP = المثلثين متشابهان مثال : إذا كان ا = PQ . LJ QM .AJKL - AMPQ 6.3 التشابه بضلعين وزاوية محصورة (SAS) إذا كان طولا ضلعين في مثلث ما متناسبين مع طولي الضلعين المناظرين لهما في مثلث آخر وكانت الزاويتان المحصورتان بينهما متطابقتين، فإن المثلثين متشابهان. ST RS مثال إذا كان = = . فإن ARST - AXYZ النظرية 6.2 ستبرهن النظرية 6.3 في السؤال 17 H F B A F K H JG FG = برهان اكتب برهانا حرا للنظرية 6.2 المعطيات: المطلوب: AB BC AC FG GH FH AABC AFGH البرهان عين النقطة ( على FG ، بحيث يكون JG = AB . ارسم JK، بحيث يكون JK || FH . سم GJK بالرمز 21 . بما أن LG G وفق خاصية الانعكاس و F = 1 وفق مسلمة الزاويتين المتناظرتين، فإنّ، GJK - AGFH وفق مسلمة التشابه AA . ومن تعريف المضلعات المتشابهة يكون . وبالتعويض ينتج أن: - JK GK = AB FH GH FG BC AB = = وبما أن: AC FH GH FG JK FH GK GH ، إذن يمكننا استنتاج أن: = FH GK BC JK GH " GK , JK = AC ، لذلك GK = BC, JK = A . ومن مسلمة التطابق SSS ، يكون AABC = AJGK . ، وهذا يعني أن: ولأن العناصر المتناظرة في المثلثين المتطابقين تكون متطابقة فإن : B = GA1 ، وبما أن: F = 1 ؛ إذن A = F وفق خاصية التعدي؛ إذن ومن مسلمة التشابه AA ، يكون AABC - AFGH . الدرس - المثلثات المتشابهة 21 Ministry of Education 2024-1446 نفسه.

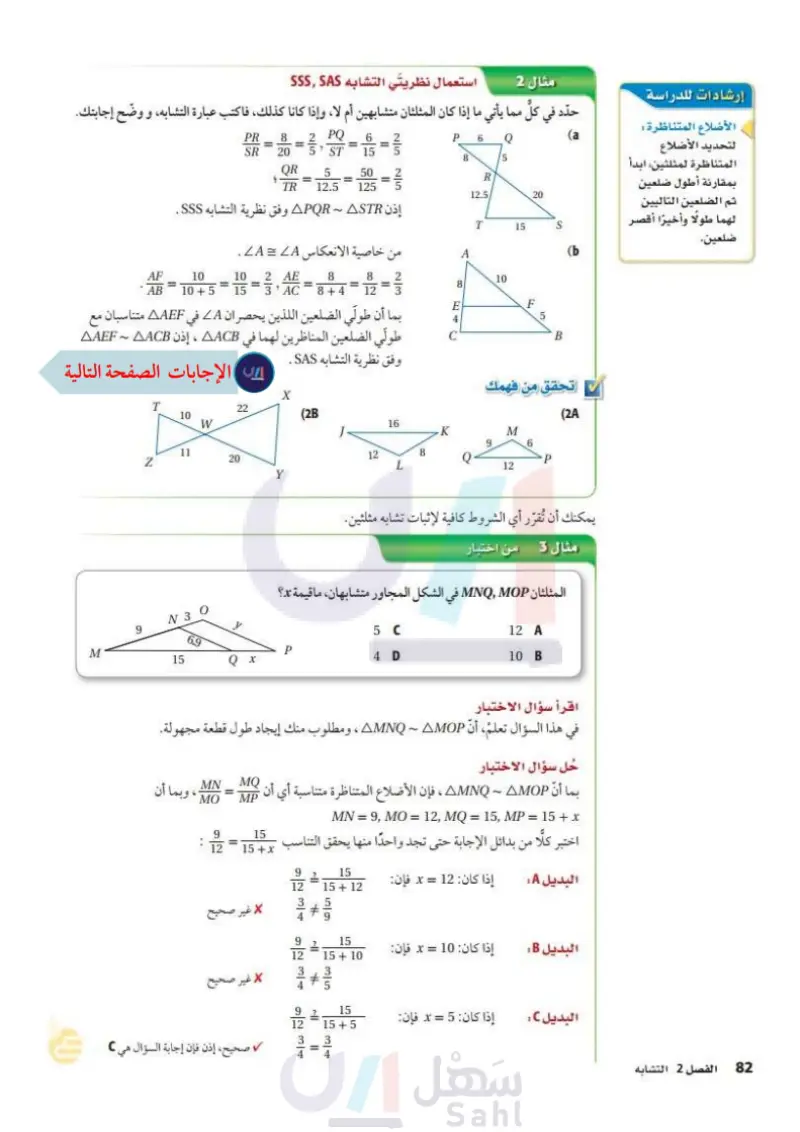
إرشادات للدراسة استعمال نظريتي التشابه SSSSAS مثال 2 حدد في كل مما يأتي ما إذا كان المثلثان متشابهين أم لا، وإذا كانا كذلك، فاكتب عبارة التشابه، و وضح إجابتك. الأضلاع المتناظرة : لتحديد الأضلاع المتناظرة لمثلثين ابدأ بمقارنة أطول ضلعين ثم الضلعين التاليين لهما طولا وأخيرا أقصر ضلعين. PR 8 2 PQ 6 2 = = = 20 5 ST 15 5 f QR 5 TR = 50 12.5 125 SR إذن APQR - ASTR وفق نظرية التشابه SSS . P 6 Q 8 5 R 12.5/ 20 T 15 S من خاصية الانعكاس A = A . A AF 10 10 2 AE AB 10+5 15 3' AC 8 8 2 10 = 8 = 8+4 12 3 E F بما أن طولي الضلعين اللذين يحصران A في AAEF متناسبان مع طولي الضلعين المناظرين لهما في AACB ، إذن AAEF - AACB وفق نظرية التشابه SAS . 5 4 C B 22 الفصل 6 التشابه تحقق من فهمك (2) 16 X T 22 10 (28) W K M 9 6 20 12 8 L P 12 Y يمكنك أن تُقرّر أي الشروط كافية لإثبات تشابه مثلثين. مثال 3 من اختبار المثلثان MNQ, MOP في الشكل المجاور متشابهان، ما قيمة x؟ 12 A 10 B Z 11 M 9 30 5 C 6.9 P 4 D 15 Q x اقرأ سؤال الاختبار في هذا السؤال تعلم، أن AMNQ - AMOP ، ومطلوب منك إيجاد طول قطعة مجهولة. حل سؤال الاختبار بما أن AMNQ - AMOP ، فإن الأضلاع المتناظرة متناسبة أي أن - MN = 9, MO = 12, MQ = 15, MP = 15 + x اختبر كلًا من بدائل الإجابة حتى تجد واحدا منها يحقق التناسب . MN ، وبما أن MO = MQ MP 15 15 + x 9 : = 12 إذا كان: 12 = x فإن: البديل A إذا كان 10 = x فإن البديل B : إذا كان: 5 = x فإن: البديل : 9 12 15 15+ 12 3 + 9 9 15 12 15+ 10 3 9 12 15 15+5 3 3 4 4 غير صحيح غير صحيح صحيح، إذن فإن إجابة السؤال هي . وزارة التعليم Ministry of Education 2024-1446

تحقق من فهمك (3) في المثال السابق، ما قيمة y؟ 20.7 D 9.2 C 8.4 B 5.2 A استعمال المثلثات المتشابهة: تشابه المثلثات مثل تطابق المثلثات يحقق خصائص الانعكاس والتماثل والتعدي. اضف إلى مطويتك 3 y x ADEF~ نظرية 6.4 خصائص المثلثات المتشابهة خاصية الانعكاس للتشابه : AABC – AABC إذا كان AABC - DEF ، فإن AABC خاصية التماثل للتشابه إذا كان ABC - ADEF, DEF - XYZ خاصية التعدي للتشابه فإن AABC - AXYZ . ستبرهن النظرية 6.4 في السؤال 18 أجزاء المثلثات المتشابهة مثال 4 أوجد طول BEAD في الشكل المجاور. 3.5 بما أن BE || CD ، فإن : LABE = ACD, AEB = ADC ؛ لأنها زوايا متناظرة، ومن مسلمة التشابه ،AA ، يكون AABE - ACD. تعريف المضلعات المتشابهة C D E 3 AC = 5, CD = 3.5, AB = 3, BE = x AB BE = AC CD 3 x = 5 3.5 (3.5) 3-5.x 2.1 = x وعليه فإن BE يساوي 2.1 خاصية الضرب التبادلي بقسمة كلا الطرفين على 5 تعريف المضلعات المتشابهة AC = 5, AB = 3, AD = y + 3, AE = y خاصية الضرب التبادلي خاصية التوزيع AC AD = AB AE 5 y+3 3 = У 5.y=3(y+3) بطرح 3 من كلا الطرفين بقسمة كلا الطرفين على 2 WR, RT (4B S 8 R 2x+6 W. T x+6 10 V الدرس 2- المثلثات المتشابهة 23 Ministry of Education 2024-1446 5y = 3y + 9 2y = 9 y = 4.5 وعليه فإن : 7.5 = 3 + AD = y تحقق من فهمك أوجد كل طول فيما يأتي. x P QP, MP (4A M 6 5

إرشادات للدراسة تحويل الوحدات: 12in = 1 ft 3 in = ft = 0.25 ft مثال 5 من واقع الحياة القياس غير المباشر ، أفعوانية، يريد تركي أن يقدر ارتفاع الأفعوانية في مدينة الألعاب، فلاحظ أنه عندما كان طول ظله 38. كان طول ظل الأفعوانية 400. إذا كان طول تركي 500 و 3. فكم قدما ارتفاع الأفعوانية؟ افهم المعطيات طول ظل تركي 3ft ، وطول ظل الأفعوانية 40ft ، وطول تركي ft 5 و in 3 المطلوب: ارتفاع الأفعوانية. ارسم مخططاً توضيحيا. ft 5 و in 3 تساوي ft 5.25 5.25 ft 3 ft 40 ft- ام أي أن ft و 3in تساوي 5.25 ft إرشادات لحل المسألة حدد الإجابات المعقولة : عندما تحل مسألة تحقق من معقولية إجابتك في هذا المثال، طول ظل تركي أكبر بقليل من نصف طوله، وكذلك طول ظل الأفعوانية أكبر من نصف ارتفاعها بقليل لذا فالإجابة معقولة. خطط في مسائل الظل افترض أنّ الزاويتين المتكونتين من شعاعي الشمس وأي جسمين رأسيين تكونان متطابقتين، وأن المثلث المتشكل من الجسم والأرض وشعاع الشمس المار بقمة الجسم قائم الزاوية، وبما أن هناك زوجين من الزوايا المتطابقة، فإن المثلثين القائِمي الزاوية متشابهان وفق مسلمة التشابه AA ؛ إذن يمكن كتابة التناسب الآتي: طول ظل تركي طول تركي = طول ظل الأفعوانية ارتفاع الأفعوانية حل افترض أن ارتفاع الأفعوانية يساوي x وعوض القيم المعلومة. 5.25 3 = X 40 3.x=40(5.25) 3x = 210 x = 70 بالتعويض خاصية الضرب التبادلي بالضرب بقسمة كلا الطرفين على 3 إذن ارتفاع الأفعوانية يساوي 70ft . تحقق طول ظل الأفعوانية يساوي 13.3 مرة تقريباً من طول ظل تركي تحقق لترى ما إذا كان ارتفاع 40 الأفعوانية يساوي 13.3 = 1 مرة من طول تركي 13.3 اتحقق من فهمك 70 ft 5.25 ft (5) بنايات يقف منصور بجوار بناية، وعندما كان طول له ft ، كان طول ظل البناية ft 322.5 إذا كان طول منصور 6ft ، فكم قدما ارتفاع البناية؟ أضف إلى مطويتك نظرية التشابه SAS وزارة التعليم Ministry of Education 2024-1446 B X Y C Z ZA ZX, AB CA 'XY ZX إذا كانت فإن: AABC - AXYZ X تشابه المثلثات نظرية التشابه SSS B Z AB_BC_CA -= XY YZ ZX Y إذا كانت فإن: AABC - AXYZ ملخص المفهوم مسلمة التشابه AA B বর C إذا كانت 2 = LA = X, C فإن : ABC - AXYZ الفصل 6 التشابه 24

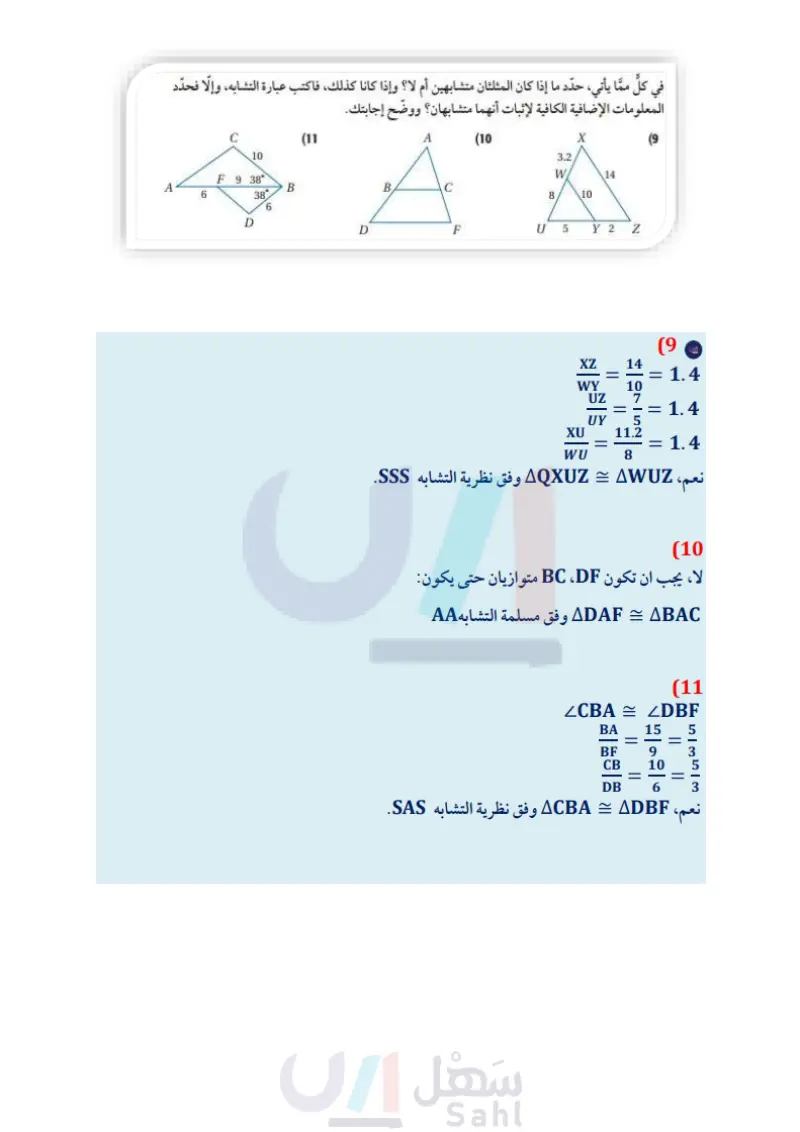
تأكد في كل مما يأتي حدد ما إذا كان المثلثان متشابهين أم لا؟ وإذا كانا كذلك فاكتب عبارة التشابه، ووضح إجابتك. المثالان 12 (2 S 20 \10 4 8 K 15 L R 6 B 3 A 4 D 10 F X V (1 Y W V F 8 5 T 12 8 G U H (5) اختيار من متعدد استعمل الشكل أدناه في إيجاد ارتفاع الشجرة؟ المثال 3 000 000000 144 ft. -120 ft- 000000 000000 00 00 5 3 R V T -x 12 264 ft A 60 ft B 72ft C 80 ft D جبر أوجد الطول المطلوب في كل من السؤالين الآتيين: المثال 4 VS (7 X KL (6 K 5 51° x 51° Y 15 Z L (8) اتصالات طول ظلّ برج اتصالات في لحظة معينة 100ft، وبجواره لوحة تحذيرية مثبتة على عمود طول المثال 5 ظله في اللحظة ذاتها ft و 4in ، إذا كان ارتفاع عمود اللوحة Aft و 6in ، فما ارتفاع البرج؟ تدرب وحل المسائل في كل مما يأتي، حدد ما إذا كان المثلثان متشابهين أم لا ؟ وإذا كانا كذلك، فاكتب عبارة التشابه، وإلا فحدّد الأمثلة 3-1 المعلومات الإضافية الكافية لإثبات أنهما متشابهان؟ ووضح إجابتك. C (11) 10 F 9 38 A B 6 38' 6 D الدرس 2- المثلثات المتشابهة 25 Ministry of Education 2024-1446 A (10 B C X (9 3.2 W/ 14 8 10 D F U 5 Y 2 Z

المثال 4 جبر أوجد الطول المطلوب في كل مما يأتي: DB, CB (14 A W WZ, UZ (13 JK (12 x K D 20 3x-6 2x + 1 4 40 L 6 22° 22° C 12 F 2x - 1 B Z x+6 U 32 P 12 M المثال 5 15) رياضة : يقف أيمن بجوار مرمى كرة السلة. إذا كان طول أيمن ft و llin، وطول ظله 2ft ، وكان طول ظل مرمى كرة السلة في اللحظة ذاتها ft و 4in، فما ارتفاع المرمي تقريبا؟ | (16) رياضة : رمى عبد الله الكرة لترتد نحو أحمد، فارتطمت بسطح الأرض على بعد المسافة بينهما، وكانت الزاويتان الناتجتان عن مسار الكرة وسطح الأرض متطابقتين. إذا رمى عبدالله الكرة من ارتفاع 40in عن سطح الأرض، فعلى أن ارتفاع سيلتقطها أحمد؟ أحمد عبد الله A DP PB D 40 in: برهان اكتب برهانا ذا عمودين في كل مما يأتي: 17) النظرية 6.3 18) النظرية 6.4 (19) المعطيات AXYZ و AABC قائما الزاوية 20 المعطيات ABCD شبه منحرف. XY YZ AB BC المطلوب إثبات أن AYXZ - BAC المطلوب إثبات أن . B P 44 B الربط مع الحياة يحدث قصر النظر عندما تجمع عدسة العين أشعة الضوء أمام الشبكية ويحدث طول النظر عندما تجمع عدسة العين أشعة الضوء خلف الشبكية. (21) رؤية : عندما ننظر إلى جسم، فإن صورته تُسْقَط على الشبكية عبر البؤبؤ، وتكون المسافتان من البؤبؤ إلى أعلى الجسم وأسفله متساويتين، والمسافتان من البؤبؤ إلى أعلى الصورة وأسفلها على الشبكية متساويتين أيضًا. هل المثلثان المتكوّنان بين الجسم والبؤبؤ وبين البؤبؤ والصورة متشابهان؟ وضح إجابتك. C الصورة على الشبكية D A الجسم E وزارة التعليم Ministry of Education 2024-1446 الفصل 6 التشابه 26

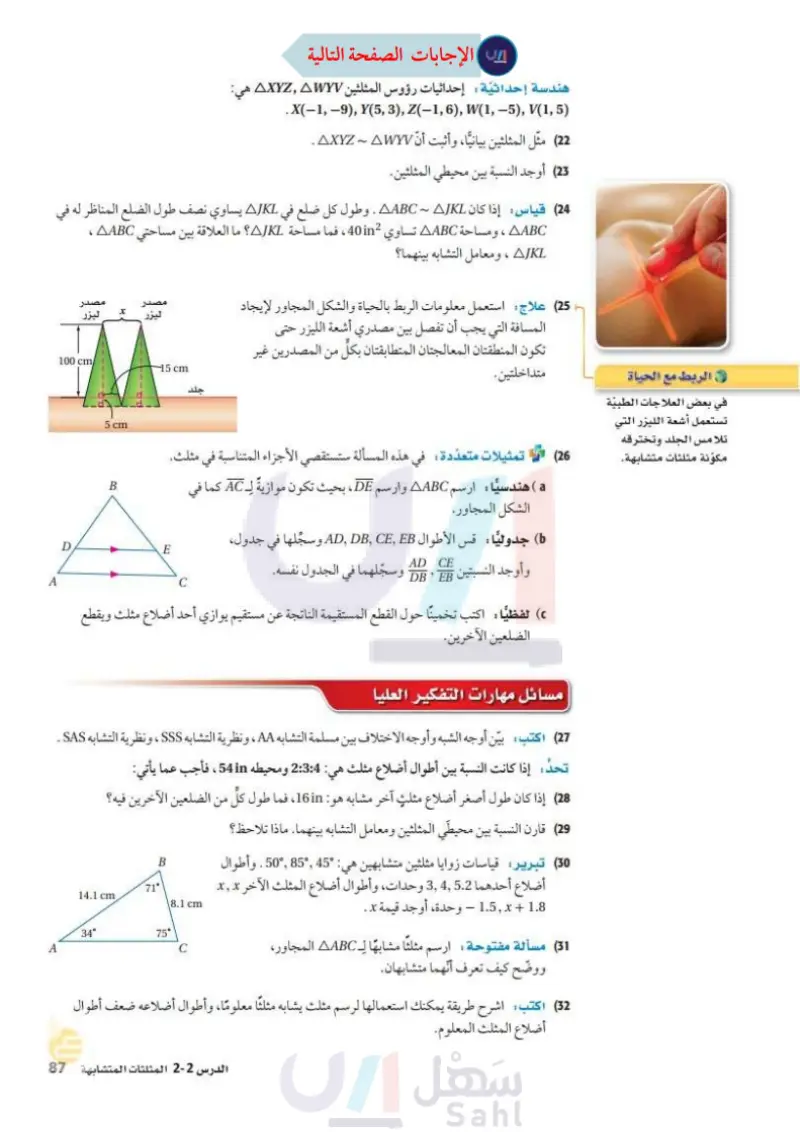
هندسة إحداثية: إحداثيات رؤوس المثلثين XYZYV هي: .X(-1, -9), Y(5, 3), Z(-1, 6), W(1,-5), V(1, 5) (22) مثل المثلثين بيانيا، وأثبت أن AXYZ - AWY . (23) أوجد النسبة بين محيطي المثلثين. 24 قياس إذا كان ABC - AJKL ، وطول كل ضلع في AJKL يساوي نصف طول الضلع المناظر له في AABC ، ومساحة ABC تساوي 40in2 ، فما مساحة AJKL؟ ما العلاقة بين مساحتي AABC ، AJKL ، ومعامل التشابه بينهما ؟ (25) علاج: استعمل معلومات الربط بالحياة والشكل المجاور لإيجاد المسافة التي يجب أن تفصل بين مصدري أشعة الليزر حتى تكون المنطقتان المعالجتان المتطابقتان بكل من المصدرين غير مصدر ليزر x مصدر ليزر 100 cm/ 15 cm الربط مع الحياة متداخلتين. في بعض العلاجات الطبية تستعمل أشعة الليزر التي تلامس الجلد وتخترقه 5 cm مكونة مثلثات متشابهة. (26) تمثيلات متعدّدة في هذه المسألة ستستقصي الأجزاء المتناسبة في مثلث. a) هندسيا : ارسم AABC وارسم DE ، بحيث تكون موازية لـ AC كما في الشكل المجاور. (6) جدوليا : قس الأطوال AD, E, E وسجلها في جدول وأوجد النسبتين AD CE DB'EB وسجلهما في الجدول نفسه. B D E C لفظيا : اكتب تخمينا حول القطع المستقيمة الناتجة عن مستقيم يوازي أحد أضلاع مثلث ويقطع الضلعين الآخرين. مسائل مهارات التفكير العليا A (27) اكتب بين أوجه الشبه وأوجه الاختلاف بين مسلمة التشابه AA ، ونظرية التشابه SSS ، ونظرية التشابه SAS . تحده إذا كانت النسبة بين أطوال أضلاع مثلث هي: 2:3:4 ومحيطه 54in ، فأجب عما يأتي: 28) إذا كان طول أصغر أضلاع مثلث آخر مشابه هو : 16in، فما طول كل من الضلعين الآخرين فيه؟ (29) قارن النسبة بين محيطي المثلثين ومعامل التشابه بينهما، ماذا تلاحظ ؟ : "8545,"50. وأطوال (30) تبرير قياسات زوايا مثلثين متشابهين هي : أضلاع أحدهما . وحدات، وأطوال أضلاع المثلث الآخر تxx 1.8 + x 1.5 - وحدة، أوجد قيمة x . (31) مسألة مفتوحة: ارسم مثلثاً مشابها لـ AABC المجاور، ووضح كيف تعرف أنهما متشابهان. 71° B 8.1 cm 14.1 cm. 34° 75° A C (32) اكتب اشرح طريقة يمكنك استعمالها لرسم مثلث يشابه مثلثا معلوما، وأطوال أضلاعه ضعف أطوال أضلاع المثلث المعلوم. الدرس - المثلثات المتشابهة 27 Ministry of Education 2024-1446

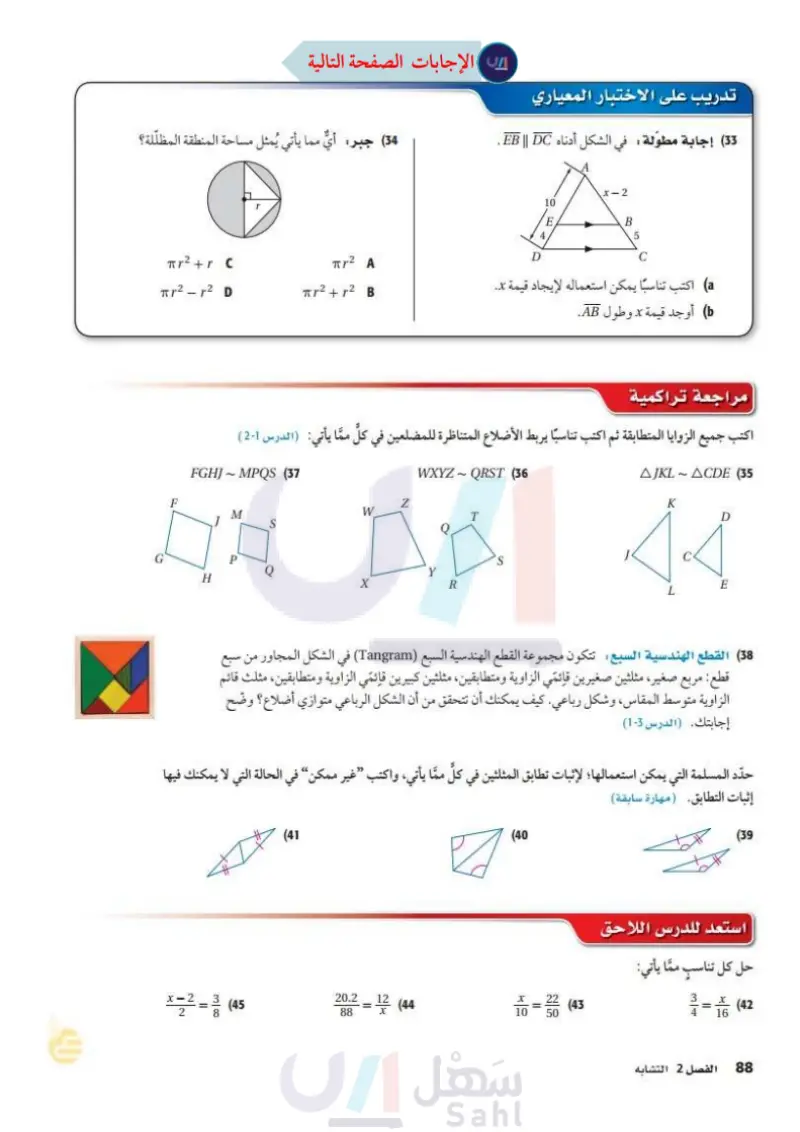
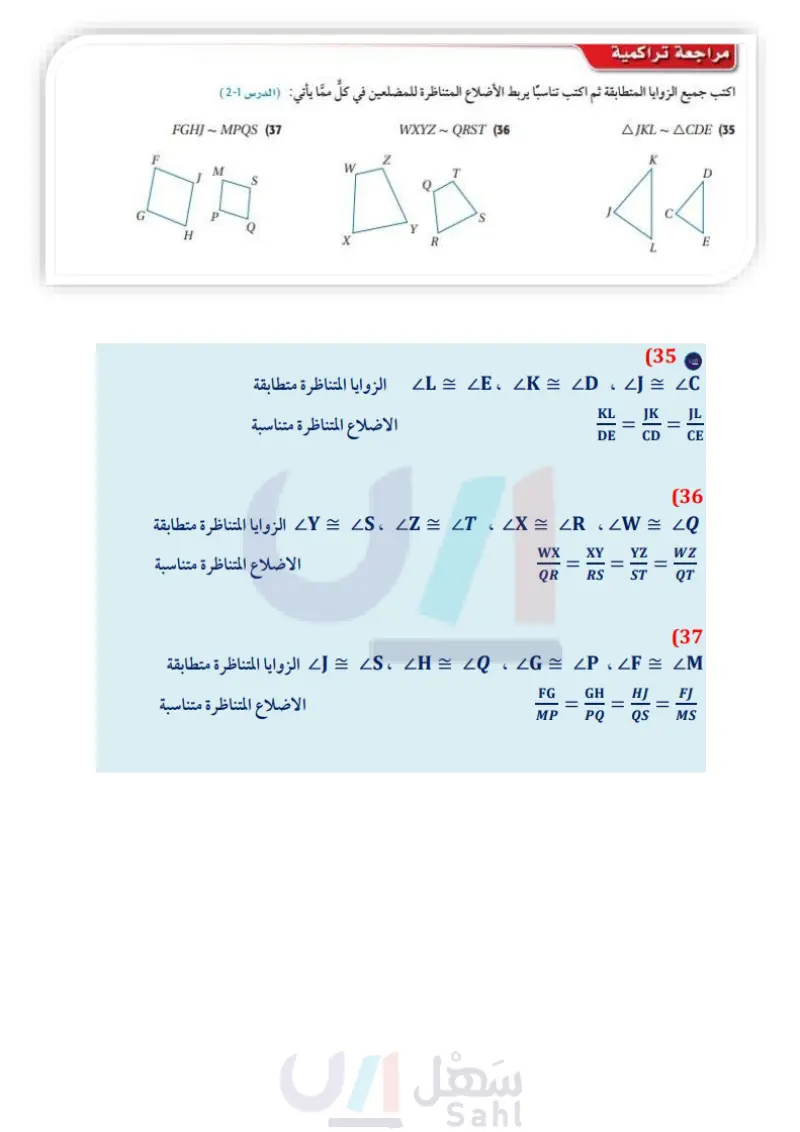
وزارة التعليم Ministry of Education 2024-1446 (34) جبر أي مما يأتي يُمثل مساحة المنطقة المظللة؟ r² + C πr² A Tr2 + 12 B تدريب على الاختبار المعياري (33) إجابة مطولة في الشكل أدناه EB || DC . D 4 x-2 10 E B 5 C (a) اكتب تناسبا يمكن استعماله لإيجاد قيمة . أوجد قيمة x وطول AB. مراجعة تراكمية اكتب جميع الزوايا المتطابقة ثم اكتب تناسبا يربط الأضلاع المتناظرة للمضلعين في كل مما يأتي: (الدرس 61 ) Z W S F FGHJ MPQS (37 M ДД P G H WXYZ - QRST (36) T S X R - AJKL ACDE (35 K D E 6 38) القطع الهندسية السبع: تتكون مجموعة القطع الهندسية السبع (Tangram) في الشكل المجاور من سبع قطع مربع صغير مثلثين صغيرين قائمي الزاوية ومتطابقين، مثلثين كبيرين قائمي الزاوية ومتطابقين، مثلث قائم الزاوية متوسط المقاس، وشكل رباعي كيف يمكنك أن تتحقق من أن الشكل الرباعي متوازي أضلاع؟ وضح إجابتك (مهارة سابقة) حدد المسلمة التي يمكن استعمالها؛ لإثبات تطابق المثلثين في كل مما يأتي، واكتب "غير ممكن“ في الحالة التي لا يمكنك فيها (41 (40) 20.2 (45) = (44 (43) 88 10 إثبات التطابق (مهارة سابقة) (39 استعد للدرس اللاحق حل كل تناسب مما يأتي: x = 4 (42) 16 الفصل 6 التشابه 28

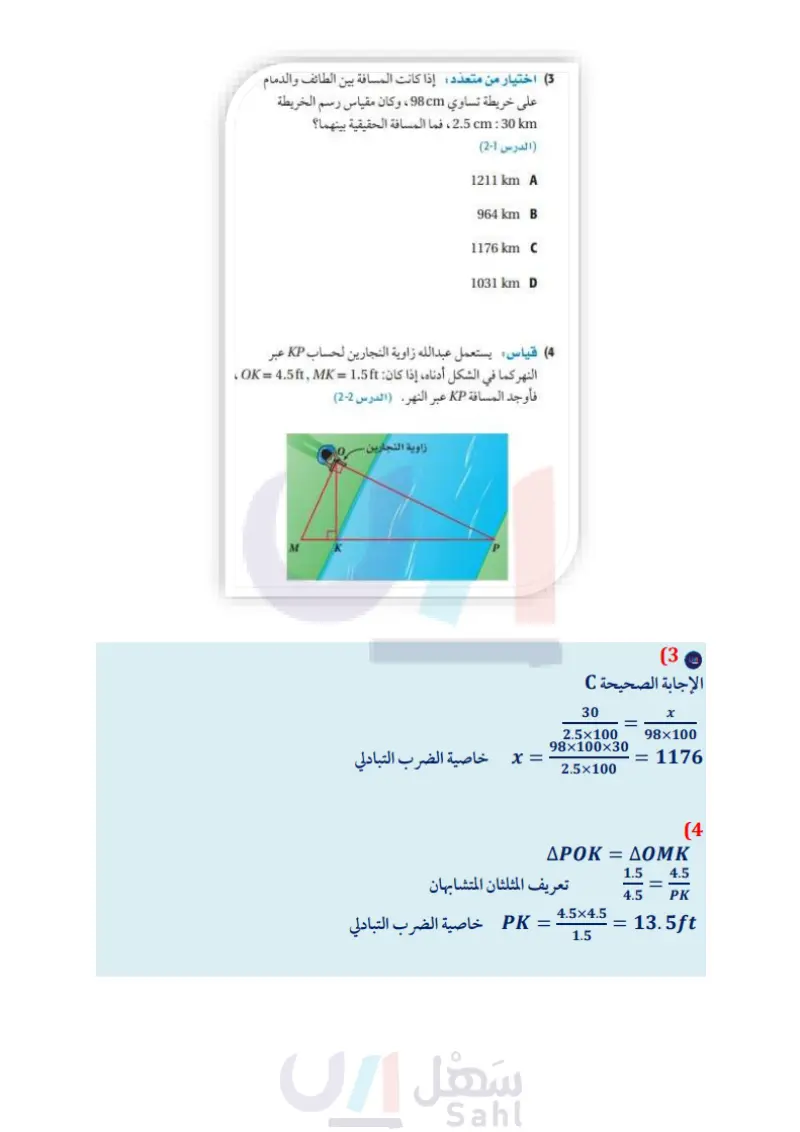
الفصل 6 اختبار منتصف الفصل الدرسان 1-6 و 2-6- إذا كان المضلعان في كل من السؤالين الآتيين متشابهين، فأوجد (5) إذا كان AWZX - ASRT، قيمة x. الدرس (1-6) (1 5 = ST = 6, WX ، فأوجد محيط AWZX إذا كان محيط ASRT يساوي 18 وحدة. (الدرس 1-6) W AA R حدد ما إذا كان المثلثان في السؤالين 67 متشابهين أم لا، وإذا كانا متشابهين، فاكتب عبارة التشابه. وإلا فحدد المعلومات الإضافية الكافية لإثبات أنهما متشابهان وضح إجابتك (الدرس (2-6) X R Z Y (6) /53" 61° F (7 AV A 61 49% CG جبر أوجد الطول المطلوب في كل من السؤالين الآتيين : ( الدرس 2-6) 16 87° K T 3 S SR (8 87 x 12 L R B 18 8 9 4 C A 10 R 工 4x + 3 S Z F x+9 20 15 T V GH (3) اختيار من متعدد: إذا كانت المسافة : ة بين الطائف والدمام على خريطة تساوي 98cm ، وكان مقياس رسم الخريطة 2.5cm : 30 km ، فما المسافة الحقيقية بينهما ؟ (الدرس 1-6) 1211 km A 964 km B 1176 km C 1031 km D (4) قياس: يستعمل عبدالله زاوية النجارين لحساب KP عبر النهركما في الشكل أدناه، إذا كان OK = 4.5 ft, MK = 1.5ft ، فأوجد المسافة KP عبر النهر (الدرس (2-6) AF (9 181 B F x زاوية النجارين - A 9 D 6 C M K P الفصل 6 اختبار منتصف الفصل الت 29م Ministry of Education 2024-1446