ضرب المصفوفات - الرياضيات العلمي - خامس اعدادي
الفصل الأول: اللوغاريتمات
الفصل الثاني: المتتابعات
الفصل الثالث: القطوع المخروطية
الفصل الرابع: الدوال الدائرية
الفصل الخامس: الغاية والاستمرارية
الفصل السادس: المشتقات
الفصل السابع: الهندسة الفضائية (المجسمة)
الفصل الثامن: مبدأ العد (التباديل والتوافيق)
الفصل التاسع: المصفوفات
ضرب المصفوفات
شروط ضرب B*A هي أعمدة A تساوي صفوف B
إذا كانت A=[2 -3 4 5],B=[1 0 3 2 1 0] فجد إن أمكن A*B
لا يمكن إيجاد A*B لأن أعمدة B≠ صفوف A
إذا كانت A=[3 5 0 4],B=[2 0 3 5] فأثبت أن عملية ضرب المصفوفة غير إبدالية
إذا كانت A=[a11 a12 a21 a22],I=[1 0 0 1] فأثبت أن I*A=A*I وماذا تستنتج من ذلك
مصفوفة محايده بالنسبة لعملية ضرب المصفوفة المربعة من النوع 2*2
إذا علمت أن [1 0 -1][1 -2 3]=[x y z] فجد كلا من x,y,z
إذا علمت أن A مصفوفة من النوع 2X3، B مصفوفة من النوع 3x2 فجد نوع كل من المصفوفات الآتية A*B
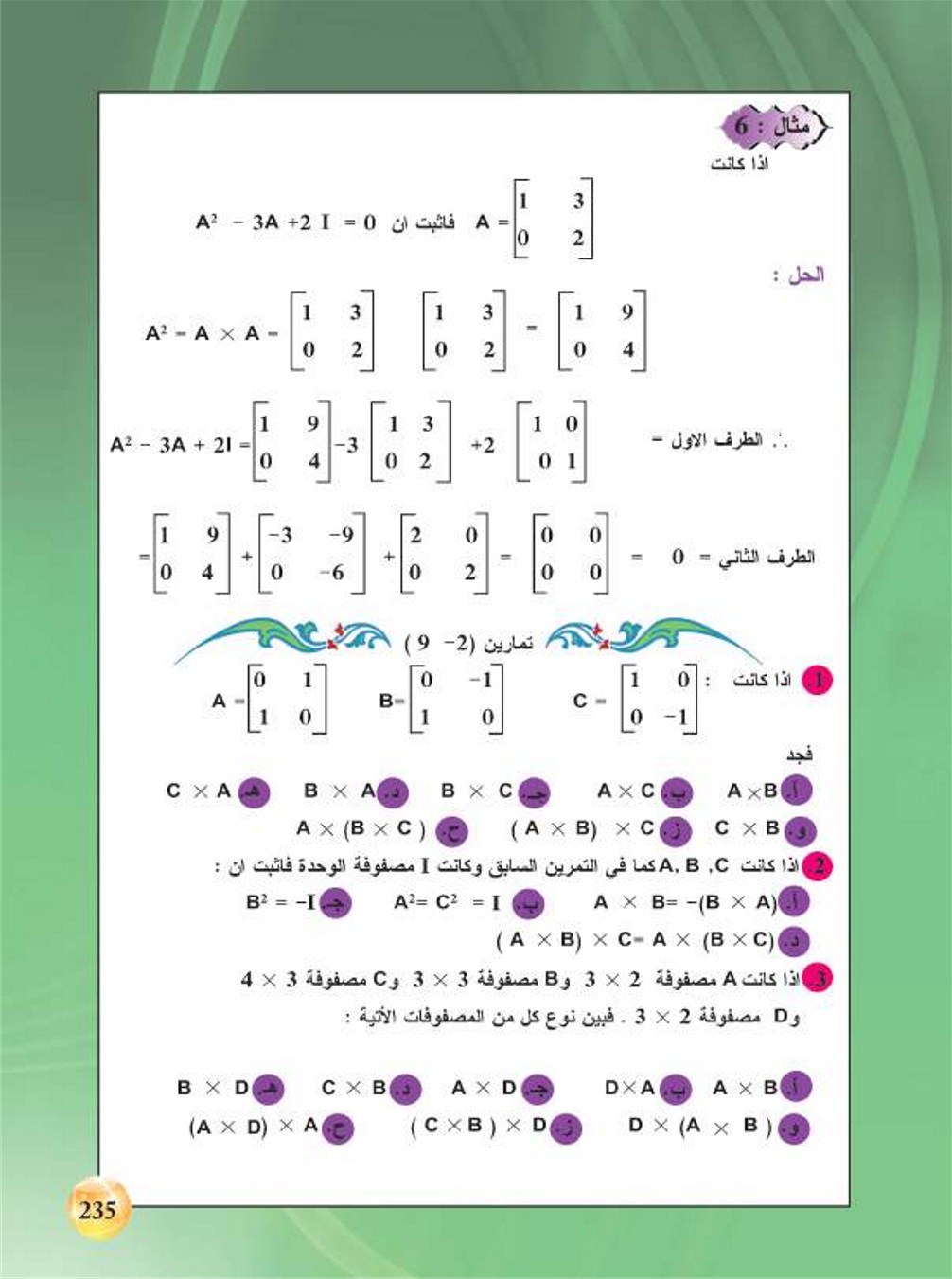
إذا كانت A=[1 3 0 2] فأثبت أن A^2*3A+2I=0
