الزاوية الزوجية والمستويات المتعامدة - الرياضيات العلمي - سادس اعدادي
الفصل الأول: الأعداد المركبة
الفصل الثاني: القطوع المخروطية
الفصل الثالث: تطبيقات التفاضل
الفصل الرابع: التكامل
الفصل الخامس: المعادلات التفاضلية الاعتيادية
الفصل السادس: الهندسة الفضائية
زينب عبدالوهاب
- حيدر وليد 03:03
01:26
(0)
0
الزاوية الزوجية والمستويات المتعامدة
حرف الزاوية الزوجية
الزاوية الزوجية بين المستويين
قياس الزاوية الزوجية
الزاوية العائدة للزاوية الزوجية
الزاوية المستوية العائدة لزاوية زوجية
إذا كانت الزاوية الزوجية قائمة فإن المستويين متعامدان وبالعكس
مبرهنة 7: إذا تعامد مستويان فالمستقيم المرسوم في أحدهما والعمودي على مستقيم التقاطع يكون عموديا على المستوي الآخر
نتيجة مبرهنة 7 إذا تعامد مستويان فالمستقيم المرسوم في أحدهما والعمودي على مستقيم التقاطع يكون عموديا على المستوي الآخر
مبرهنة 8: كل مستو مار بمستقيم عمودي على مستو آخر يكون عموديا على ذلك المستوي
المطلوب إثباته من مبرهنة 8
مبرهنة 9 من مستقيم غير عمودي على مستو معلوم يوجد مستو وحيد عمودي على المستوي المعلوم
المطلوب إثباته من مبرهنة 9
نتيجة مبرهنة 9 إذا كان كل من مستويين متقاطعين عموديا على مستو ثالث فإن مستقيم تقاطعهما يكون عموديا على المستوي الثالث
في ΔABC: BD⊥(ABC),m∠A=30° AB=10cm,BD=5cm جد قياس الزاوية الزوجية D-AC-B
ليكن ABC مثلثا وليكن AF⊥(ABC), BD⊥CF, BE⊥CA
(Y),(X) مستويان متعامدان AB⊂(X), BC,BD عموديان على AB ويقطعان (Y) في C,D على الترتيب
برهن أن مستوي الزاوية المستوية العائدة لزاوية زوجية يكون عمودياً على حرفها
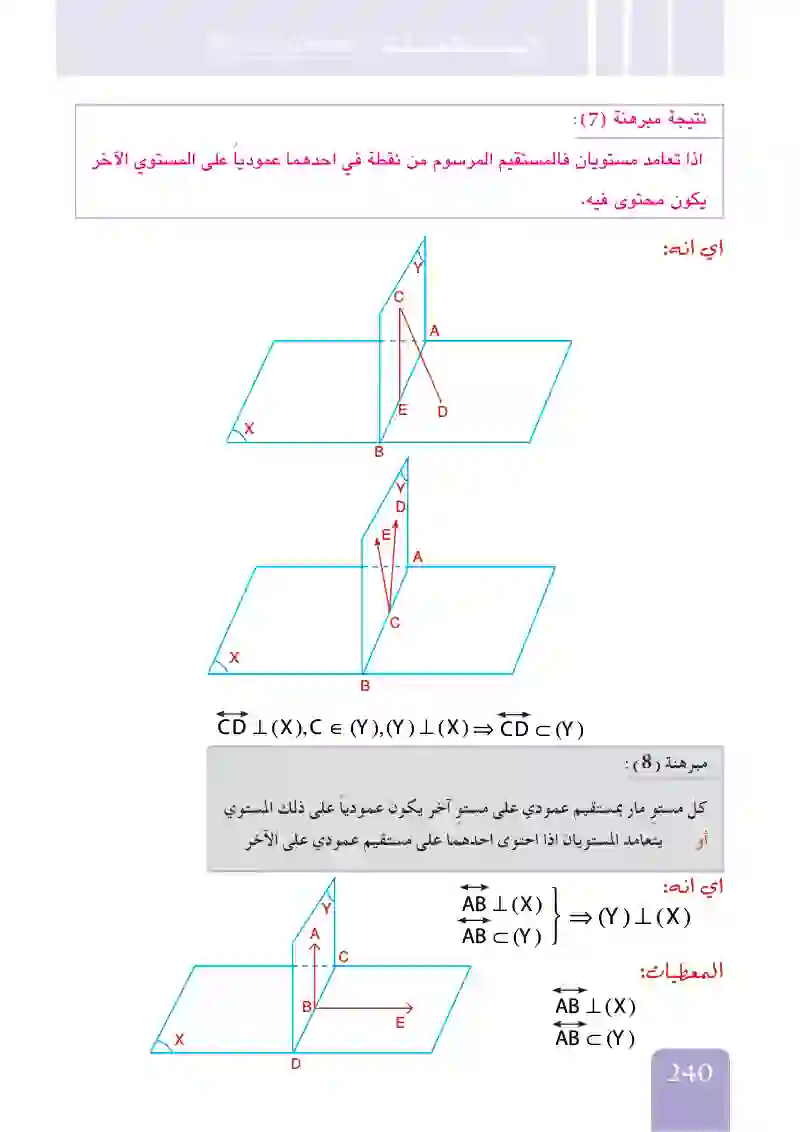
A,B,C,D أربع نقاط ليست في مستو واحد بحيث E∈BC ,AB = AC فإذا كانت ∠AED عائدة للزاوية الزوجية برهن أن CD = BD
برهن أنه إذا وازى كل من مستقيمين متقاطعين مستوياً معلوماً وكانا عموديين على مستويين متقاطعين فإن مستقيم تقاطع المستويين المتقاطعين يكون عموديا على المستوي المعلوم
دائرة قطرها AC ، AB عمودي على مستويها ، D نقطة تنتمي للدائرة . برهن أن (CDA) عمودي على (CDB)
برهن أن المستوي العمودي على أحد مستويين متوازيين يكون عمودياً على الآخر أيضاً
برهن أنه إذا وازی مستقیم مستوياً وكان عمودياً على مستو آخر فان المستويين متعامدان
لم يتم إضافة أي تعليقات حتى الآن.
الرجاء تسجيل الدخول لكتابة تعليق
