المجسمات - الرياضيات العلمي - سادس اعدادي
الفصل الأول: الأعداد المركبة
الفصل الثاني: القطوع المخروطية
الفصل الثالث: تطبيقات التفاضل
الفصل الرابع: التكامل
الفصل الخامس: المعادلات التفاضلية الاعتيادية
الفصل السادس: الهندسة الفضائية
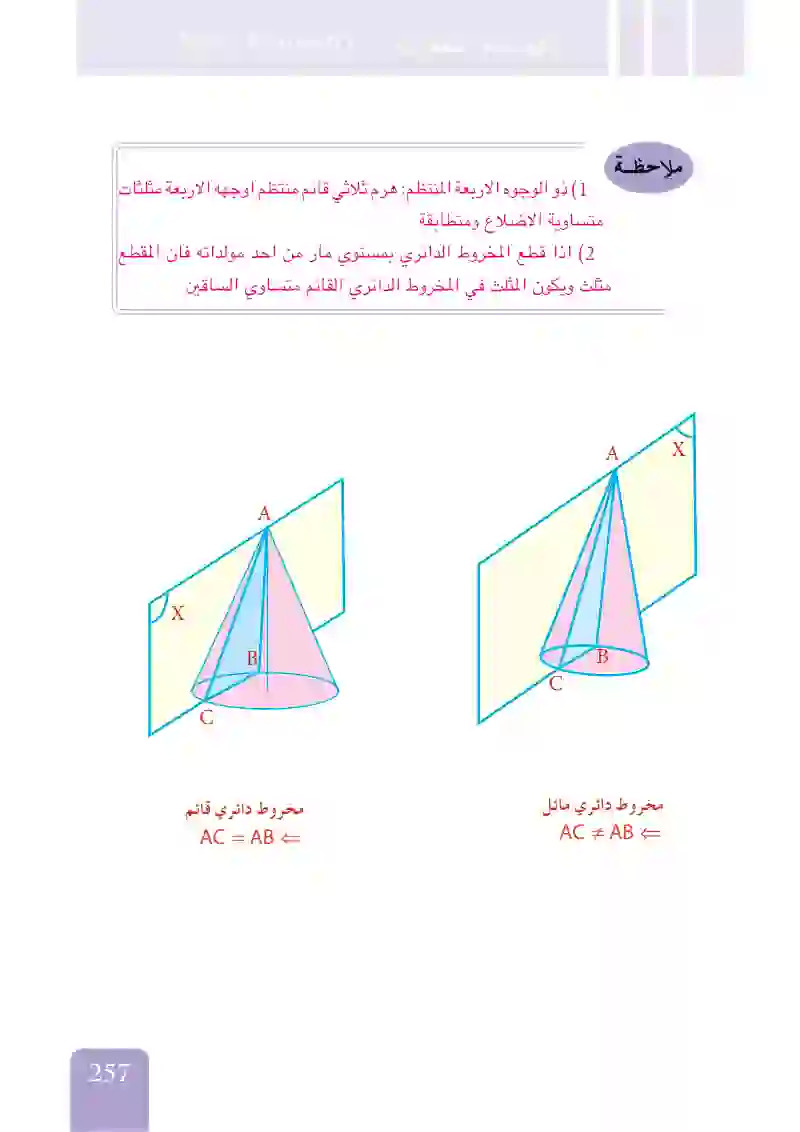
\ذو الوجوه الأربعة المنتظم

إذا كانت المساحة الكلية لمتوازي المستطيلات = 2^724cm ومساحة قاعدته = 2^132cm ومساحة أحد أوجهه الجانبية = 2^110cm جد حجمه


قطع ناقص مركزه نقطة الأصل وقطع زائد نقطة تقاطع محوريه نقطة الأصل. كل منهما يمر ببؤرة الآخر فإذا كانت 9x^2+25y^2=225 معادلة القطع الناقص فجد محيط القطع الناقص