البرهان الجبري - الرياضيات 1-1 - أول ثانوي

1-6 البرهان الجبري رابط الدرس فيما سبق: درست المسلمات الأساسية حول النقاط والمستقيمات والمستويات. (الدرس 5-1) والآن : أستعمل الجبر لكتابة برهان ذي عمودين. أستعمل خصائص Algebraic Proof الماذا؟ تحتوي بعض السيارات على شاشة لعرض درجة الحرارة الخارجية بالمقياس الفهرنهايتي أو المقياس السيليزي. والمقياس الفهرنهايتي يحدد درجة تجمد الماء عند °32 ، ودرجة غليانه عند °212، أما المقياس السيليزي فيحدد درجة تجمد الماء عند 0 ، وغليانه عند .100° www.ien.edu.sa km/h 60 180 -40 200 -20 220- 240 RANGE 8804-9 491 km ODO km 6347 OUTSIDE 20°C يمكنك استعمال البرهان الجبري؛ لإثبات أنه إذا كانت العلاقة التي تربط هذين المقياسين معطاة بالصيغة. (F) - (32) 5 9 = C ، فإنها تعطى أيضًا بالصيغة 32 + F = C البرهان الجبري: الجبر نظام مكوّن من مجموعات من الأعداد، وعمليات عليها وخصائص تمكنك المساواة لكتابة برهان إجراء هذه العمليات. والجدول الآتي يلخص عدة خصائص للأعداد الحقيقية التي ستستعملها في الجبر. هندسي المفردات: خصائص الأعداد الحقيقية من أضف إلى مطويتك البرهان الجبري algebraic proof البرهان ذو العمودين two-column proof مفهوم أساسي الخصائص الآتية صحيحة لأي ثلاثة أعداد حقيقية خاصية الجمع للمساواة خاصية الطرح للمساواة إذا كان b = ، فإن + a + c = b. خاصية الضرب للمساواة خاصية القسمة للمساواة خاصية الانعكاس للمساواة a = a خاصية التماثل للمساواة خاصية التعدي للمساواة خاصية التعويض للمساواة إذا كان a = b ، فإن a - c = b - c. إذا كان a = b ، فإن a c = a b c . . b .a. إذا كان a = b و c t o ، فإن ا = 4 0 .b إذا كان a = b ، فإن b = a . a، a C إذا كان a = b و b = c، فإن a = c. إذا كان a = b ، فإنه يمكننا أن نضع b مكان a في أي معادلة أو عبارة جبرية تحتوي على a خاصية التوزيع a(b + c)= ab + ac البرهان الجبري هو برهان يتكون من سلسلة عبارات جبرية، وتبرر خصائص المساواة أعلاه كثيرًا من العبارات المستعملة في البراهين الجبرية. مثال 1 تبرير كل خطوة عند حل المعادلة أثبت أنه إذا كان 70 54 ، فإن 18 = x اكتب تبريرا لكل خطوة. = (4) + x)5-، -5(x+4)=70 −5.x+(−5).4=70 −5x – 20 = 70 −5x – 20 + 20 = 70 + 20 -5x = 90 −5x 90 = -5 -5 x = -18 المعادلة الأصلية، أو المعطيات استعمل خاصية التوزيع بسّط استعمل خاصية الجمع للمساواة بسط استعمل خاصية القسمة للمساواة بسط الدرس 6-1 البرهان الجبري الت 53م Ministry of Education 2024-1446

إرشادات للدراسة الخوارزميات الخوارزمية هي سلسلة من الخطوات المتبعة لإجراء عملية أو حل مسألة ما. ويمكن اعتبار البرهان من أنواع الخوارزميات؛ لأنه يتم خطوة بخطوة. تحقق من فهمك اذكر الخاصية التي تبرر كلا من العبارتين الآتيتين: ― (1) إذا كان 1 = (5) + 4، فإن 1 - x + 4 + (5) = x : (1) إذا كانت y = 5 ، فإن 5 = y IC) أثبت أنه إذا كان 5 13 - 2x، فإن 4 = x. اكتب تبريرًا لكل خطوة. = - يوضح المثال 1 برهان العبارة الشرطية إذا كان 70 = 4 + x)5، فإن 18 = x". لاحظ في هذا البرهان أن العمود الأيمن يحتوي على تفصيل الطريقة التي تقود إلى الحل خطوة بخطوة، أما العمود الأيسر فيحتوي على مبرر كل خطوة. وتكتب براهين النظريات والتخمينات الهندسية عادةً على هذا النحو فيما يسمى البرهان ذو العمودين ، حيث العبارات مرتبة في عمود والتبريرات في عمود مواز. مثال 2 من واقع الحياة كتابة البرهان الجبري علوم إذا كانت الصيغة التي تحول درجات الحرارة من فهرنهايتية إلى سيليزية هي (32) - (F) ، فإن الصيغة التي تحول درجات الحرارة من سيليزية إلى 5 9 = فهرنهايتية هي 32 + F C. اكتب برهانا ذا عمودين لإثبات صحة هذا التخمين. اكتب المعطيات والمطلوب إثباته أولا. المعطيات: 32 - (C = { (F 5 9 120 C °F 50 40 100 30 80 20 60 10 40 0 32 20 10 0 20 30 20 40 40 إرشادات للدراسة رياضيات ذهنية إذا سمح معلمك، يمكنك حذف بعض الخطوات وذلك لأن بعض الحسابات يمكن إجراؤها ذهنيًا؛ ففي المثال 2 يمكن حذف العبارتين 2 و 4 ؛ ليصبح مبرر العبارة 3 "خاصية الضرب للمساواة"، والعبارة 5 "خاصية الجمع للمساواة". المطلوب : 32 + F = C البرهان : العبارات C = (F-32) (1 C=(F-32) (2 9 B C = F - 32 (3) - C+32= F - 32 + 32 (4 B C + 32 = F (5) F = √ C + 32 (6 54 الفصل 1 التبرير والبرهان تحقق من فهمك المبررات 1) معطيات (2 خاصية الضرب للمساواة (3) بالتبسيط (4) خاصية الجمع للمساواة (5) بالتبسيط (6) خاصية التماثل للمساواة اكتب برهانا ذا عمودين لإثبات صحة كل من التخمينين الآتيين: (2) إذا كان 0 = 8 - 5x1 ، فإن 3 = x . 2 2B فيزياء : إذا كانت المسافة d التي يقطعها جسم متحرك بسرعة ابتدائية U وسرعة نهائية في زمن t تعطى بالعلاقة " 1 " . d = t ، فإن v . u + 2 2d .u = - t وزارة التعليم Ministry of Education 2024-1446

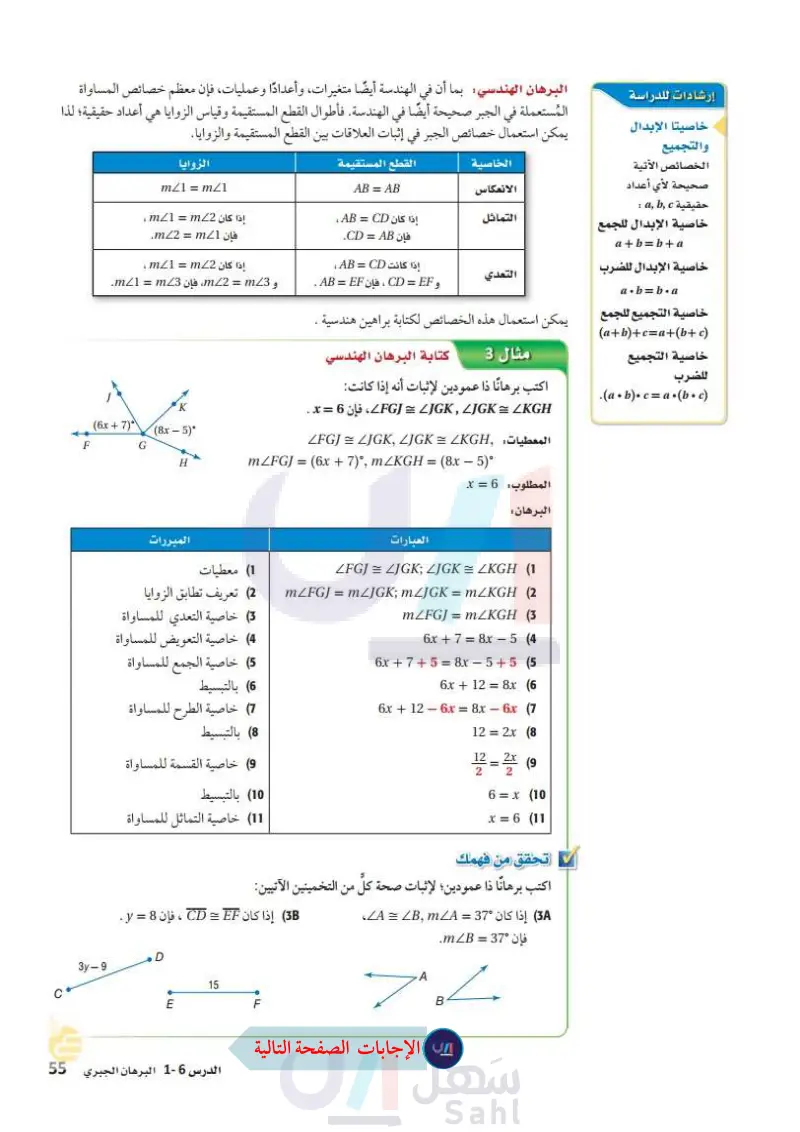
إرشادات للدراسة خاصيتا الإبدال والتجميع الخصائص الآتية صحيحة لأي أعداد حقيقية : خاصية الإبدال للجمع a + b = b + a البرهان الهندسي بما أن في الهندسة أيضًا متغيرات، وأعدادًا ،وعمليات، فإن معظم خصائص المساواة المستعملة في الجبر صحيحة أيضًا في الهندسة. فأطوال القطع المستقيمة وقياس الزوايا هي أعداد حقيقية؛ لذا يمكن استعمال خصائص الجبر في إثبات العلاقات بين القطع المستقيمة والزوايا. القطع المستقيمة AB= = AB الزوايا mZ1 = mZ1 الخاصية الانعكاس التماثل إذا كان AB = CD ، إذا كان m1 = m2 ، فإن CD = AB. فإن mZ2 = mZ1. إذا كانت AB = CD ، إذا كان m1 = m2 ، التعدي خاصية الإبدال للضرب a.b = b.a و CD = EF ، فإن AB = EF . و m2 = m3 ، فإن mZ1 = mZ3. خاصية التجميع للجمع يمكن استعمال هذه الخصائص لكتابة براهين هندسية (a+b)+c=a+(b+c) خاصية التجميع للضرب .(a•b)•ca (bc) مثال 3 كتابة البرهان الهندسي اكتب برهانا ذا عمودين لإثبات أنه إذا كانت: LFGJ = LJGK, JGK = LKGH، فإن 6 = x . المعطيات ,LFGJ = JGK, JGK = LKGH K (8x-5)° (6x + 7) ° G H mZFGJ = (6x + 7)°, mZKGH = (8x - 5)° المطلوب : 6 = x البرهان : العبارات ZFGJ ZJGK; ZJGK ≈ ZKGH (1 mZFGJ=mZJGK; mZJGK = mZKGH (2 mZFGJ=mZKGH (3 6x + 7 = 8x - 5 (4) 6x + 7 + 5 = 8x - 5 + 5 (5) 6x+12=8x (6 6x + 12 – 6x = 8x. - 6x (7 = 12 = 2x (8 12 = 2x (9 2 2 6 = x (10 x = 6 (11 تحقق من فهمك المبررات 1) معطيات (2) تعريف تطابق الزوايا (3) خاصية التعدي للمساواة (4) خاصية التعويض للمساواة (5) خاصية الجمع للمساواة (6) بالتبسيط (7) خاصية الطرح للمساواة 8 بالتبسيط (9) خاصية القسمة للمساواة 10) بالتبسيط 11) خاصية التماثل للمساواة اكتب برهانا ذا عمودين؛ لإثبات صحة كلّ من التخمينين الآتيين: (3) إذا كان °37 = LA = LB, mLA، فإن °37 = mLB. إذا كان CD = EF ، فإن 8 = y . 7A BL F D 3y-9 15 E F الدرس 6-1 البرهان الجبري الت55م Ministry of Education 2024-1446

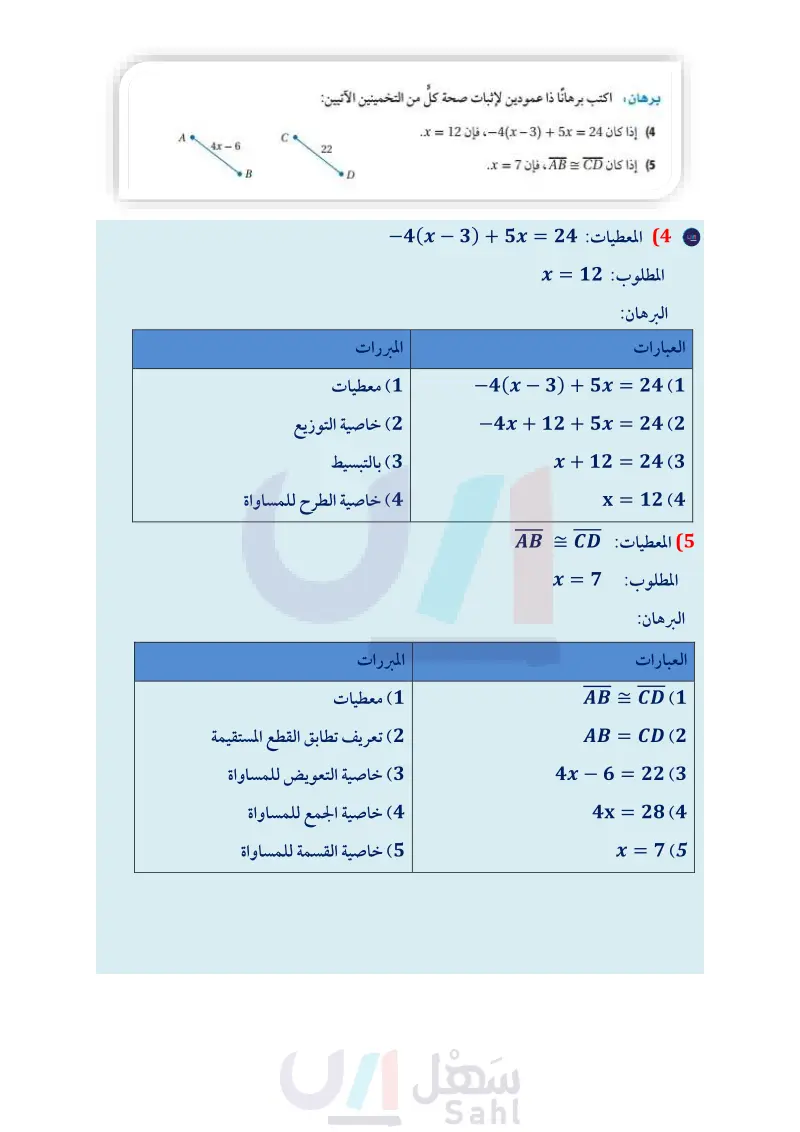
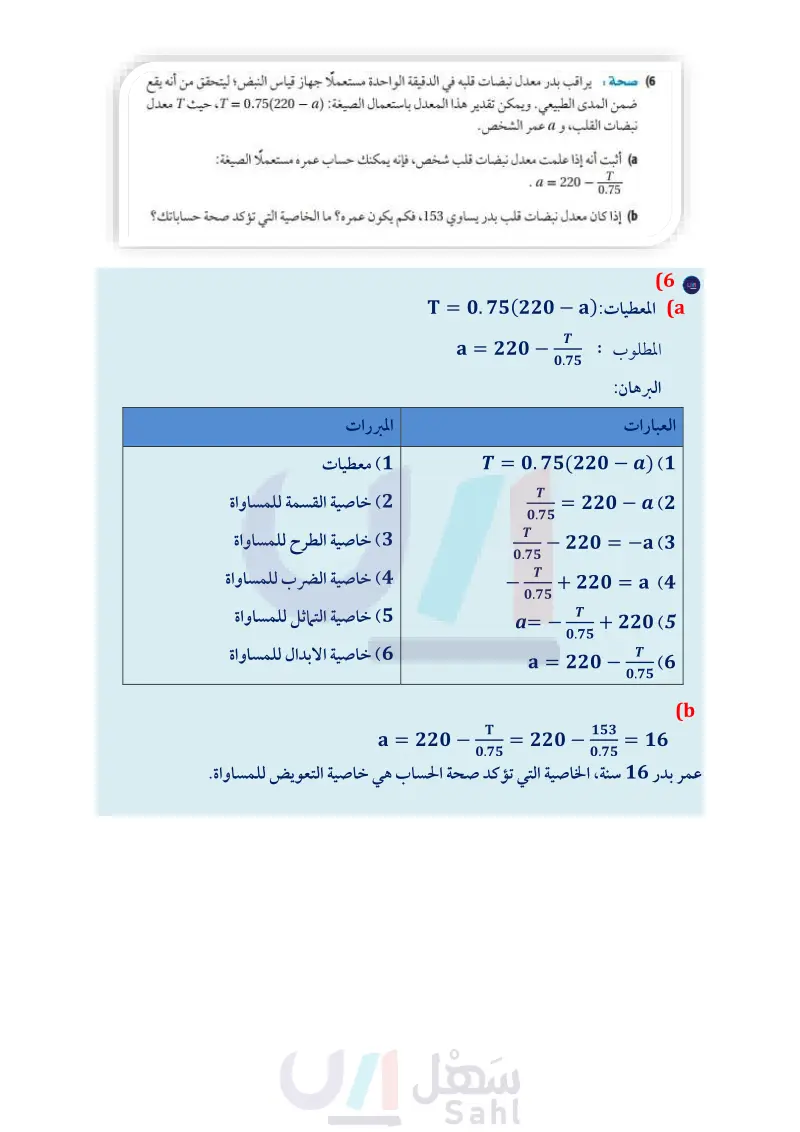
تأكـ تأكد المثال 1 اذكر الخاصية التي تبرر العبارة: 1) إذا كان x = 5، فإن 5 = x (2) أثبت أنه إذا كان 11 = 5 + 2x، فإن } = x اكتب تبريرا لكل خطوة. المثال 2 (3) أكمل البرهان الآتي: المعطيات: 3 = y + 2 3 المطلوب : 7 = y البرهان : العبارات المبررات a معطيات (b ؟ y+2 3 (3 + 2) = 3(3) (b 3 (c y = 7 (d المثالان تدرب وحل المسائل خاصية الطرح للمساواة برهان اكتب برهانا ذا عمودين لإثبات صحة كل من التخمينين الآتيين: (4 إذا كان 24 = 5 + 3 - 4x ، فإن 12 = x (3) 5x-، (5) إذا كان AB = CD ، فإن 7 = x. : C A 22 4x - 6 D B (6) صحة يراقب بدر معدل نبضات قلبه في الدقيقة الواحدة مستعملا جهاز قياس النبض؛ ليتحقق من أنه يقع ضمن المدى الطبيعي. ويمكن تقدير هذا المعدل باستعمال الصيغة : (T = 0.75 (220) - (a، حيث T معدل نبضات القلب، و a عمر الشخص. أثبت أنه إذا علمت معدل نبضات قلب شخص، فإنه يمكنك حساب عمره مستعملا الصيغة: T 0.75 . a = 220 إذا كان معدل نبضات قلب بدر يساوي ،153، فكم يكون عمره ؟ ما الخاصية التي تؤكد صحة حساباتك؟ المثال 1 اذكر الخاصية التي تبرر كل عبارة مما يأتي: (7) إذا كان 20 = 10 + a ، فإن 10 = a . (8) x إذا كان 15- = ، فإن 45- = x . = 65(x+7) (9) إذا كان 3 7 5x ، فإن 3 = 35 + 5x . 56 الفصل 1 التبرير والبرهان 2 3 (10) إذا كان 4 = - x 3، فإن 4 = 2 - 3x . . 22 (11) أثبت أنه إذا كان 2 + x = 5 )، فإن 2 = x مبررًا كل خطوة. x - وزارة التعليم Ministry of Education 2024-1446

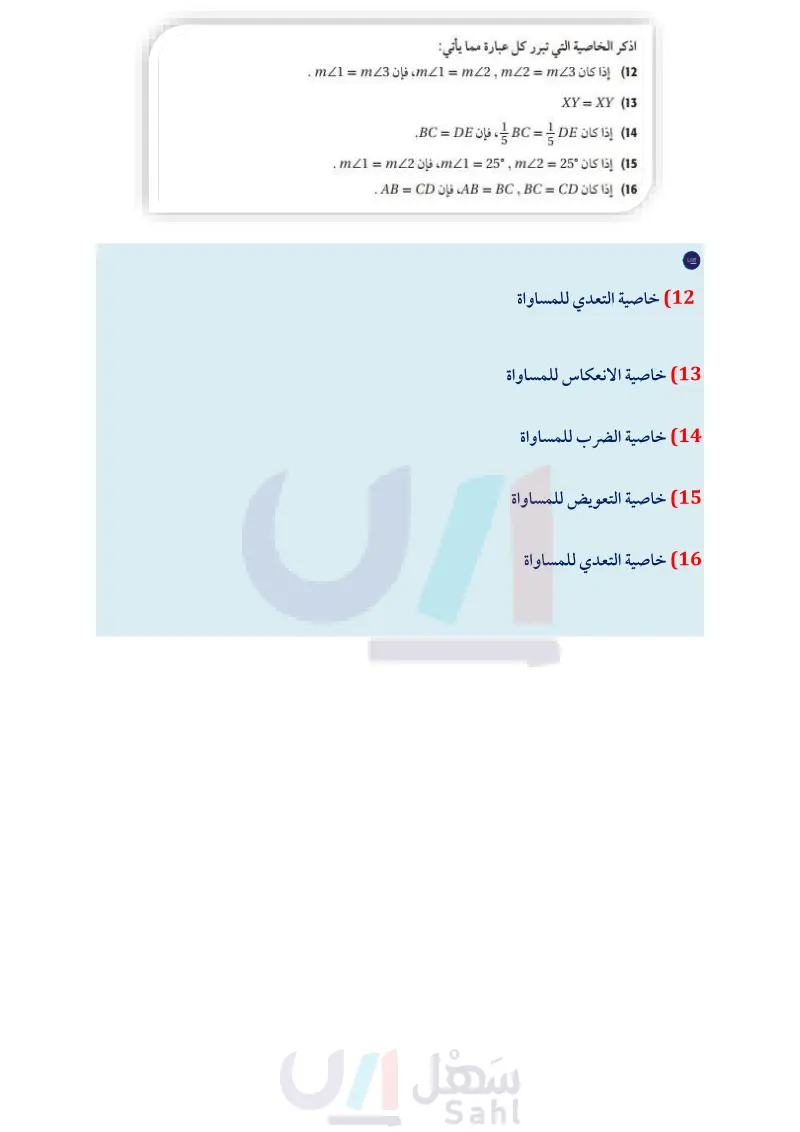
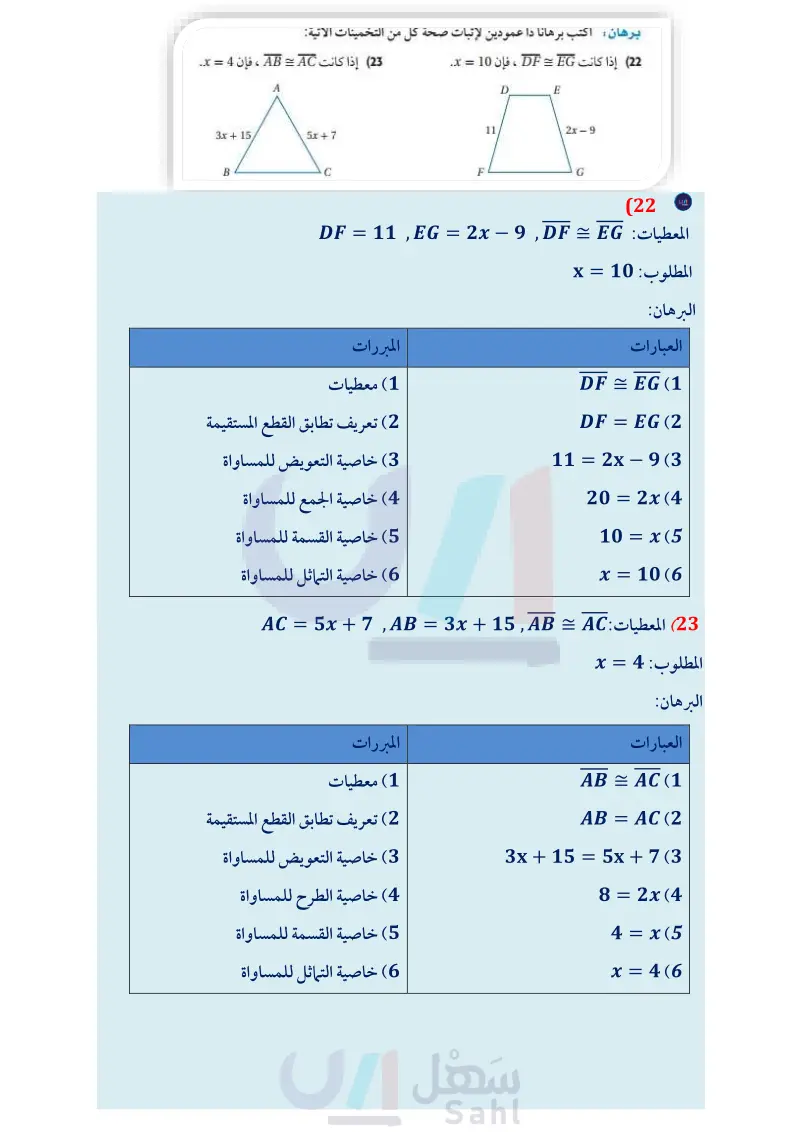
اذكر الخاصية التي تبرر كل عبارة مما يأتي: (12) إذا كان 3 m1 = mm 2 = m ، فإن m1 = m3 . XY = XY (13 (14) إذا كان BC = } DE ، فإن BC = DE. (15) إذا كان 25 = m1 = 25° m2 ، فإن m1 = m2 . " = 16 إذا كان AB - , CD ، فإن AB = CD . = المثال 2 أكمل البرهانين الآتيين: (17) المعطيات: 32 = - 8 - 3x 4 x = المطلوب : 40 البرهان : العبارات 8-3x=32 (a 4 4 (8 −3x) = 4(32) (b 8-3x=128 (c (d x = -40 (e المبررات a معطيات S (b ؟ (c (e خاصية الطرح للمساواة ؟ (18) علوم: تعطى المسافة d التي يقطعها جسم متحرك بالقدم بالصيغة : d = vt + } at2 ، حيث v سرعة الجسم بالقدم لكل ثانية، و الزمن بالثانية ، و a التسارع بالقدم لكل ثانية تربيع. اكتب برهانا ذا عمودين؛ لإثبات أن التسارع يمكن أن يُحسب بالصيغة المثال 3 برهان اكتب برهانا ذا عمودين لإثبات صحة كلّ من التخمينين الآتيين: 19) إذا كان 12 = n -، فإن 36 = n . 2d-2vt a = 12 (20) إذا كان 4 = 1 + 3-، فإن } - - (21) علوم : يُعطى قانون الغاز المثالي بالصيغة PV = nRT ، حيث : الضغط بوحدة الضغط الجوي(atm)، و V : الحجم باللترات ، و n : عدد مولات الغاز و R : ثابت الغاز المثالي، حيث 0.0821 = T ،R : درجة الحرارة بالكلفن. 6 أثبت أنه إذا كان ضغط الغاز وحجمه وعدد مولاته جميعها معلومة، فإنه يمكن حساب درجة حرارته باستعمال الصيغة = T PV nR ما درجة حرارة 1 مول من الأكسجين موجود في إناء سعته 25L ، وتحت ضغط مقداره atm 1 ؟ ما الخاصية التي تبرّر حساباتك؟ برهان اكتب برهانا ذا عمودين لإثبات صحة كلّ من التخمينات الآتية: (22) إذا كانت DF = EG ، فإن 10 = x. (23) إذا كانت AB = AC ، فإن 4 = x . A 3x + 15 5x+7 B الدرس 6-1 البرهان الجبري الت 57م Ministry of Education 2024-1446 D E 2x - 9 A 11 G C F

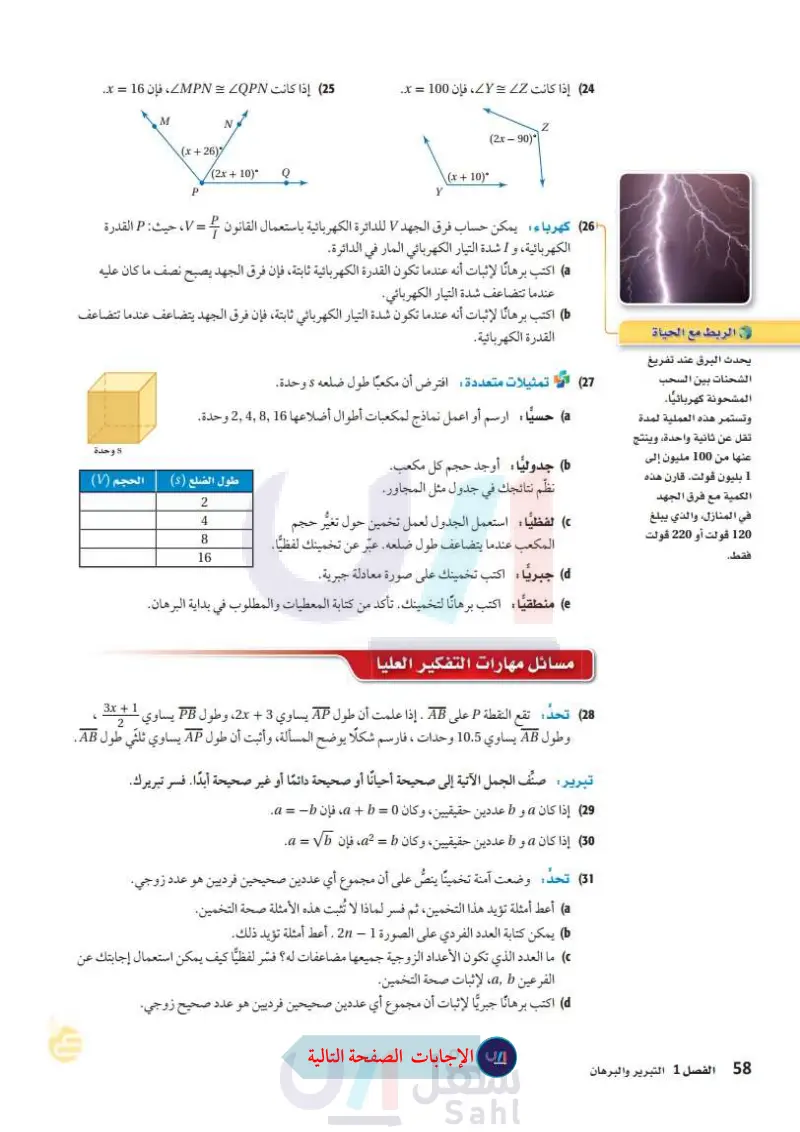
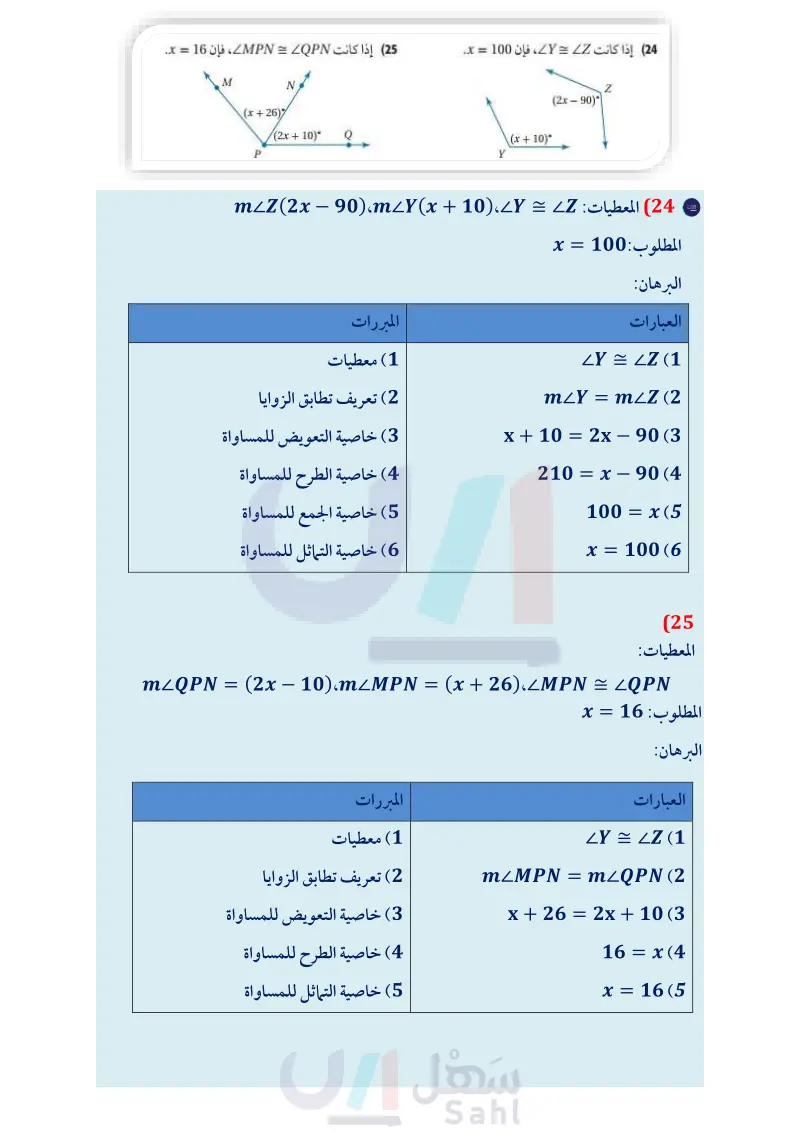
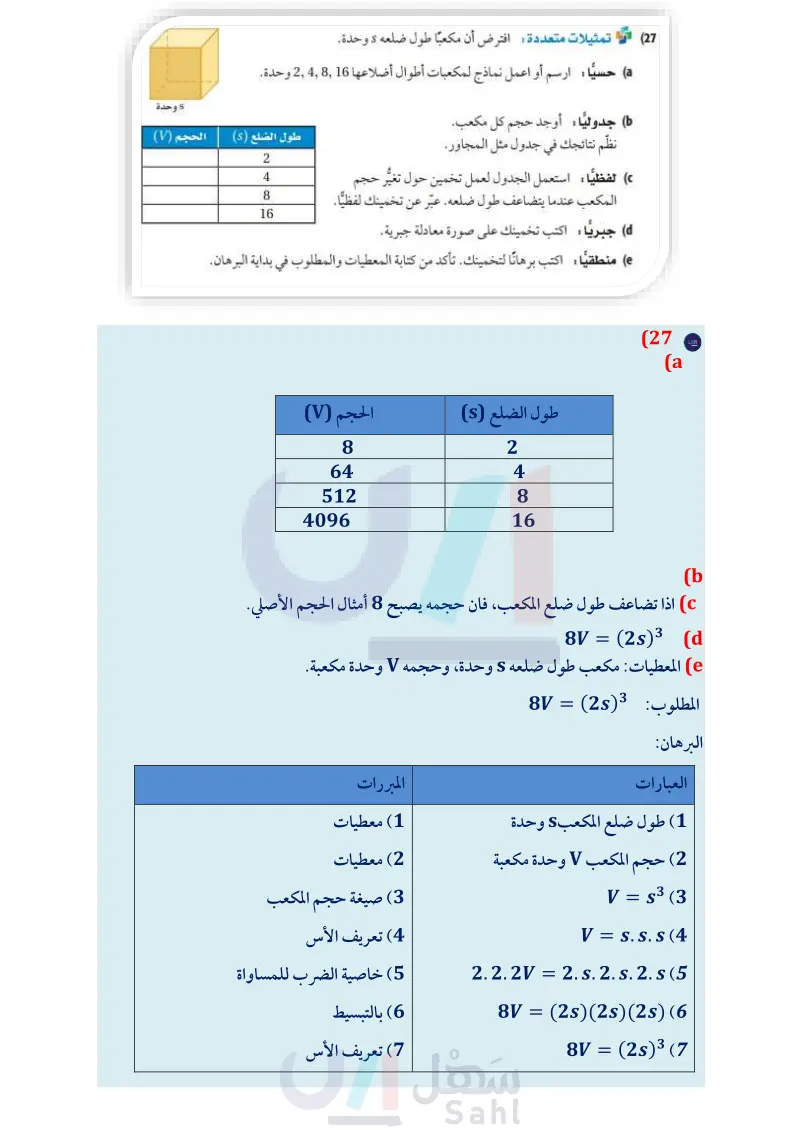
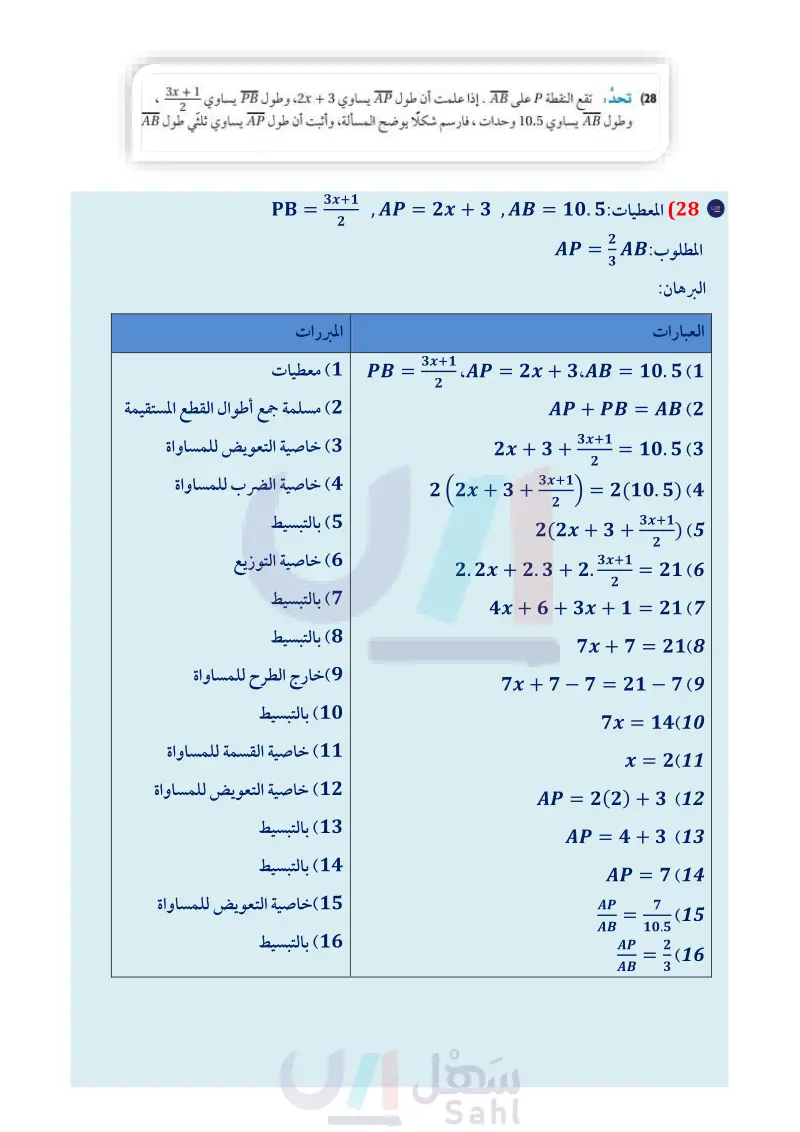
(24) إذا كانت 2 = ، فإن 100 = x . (25) إذا كانت MPN = LQPN، فإن 16 = x. M N (x+26) (2x + 10)° P P Z (2x-90) (x + 10)° Y الربط مع الحياة يحدث البرق عند تفريغ الشحنات بين السحب المشحونة كهربائيا. وتستمر هذه العملية لمدة تقل عن ثانية واحدة، وينتج عنها من 100 مليون إلى 1 بليون قولت. قارن هذه الكمية مع فرق الجهد في المنازل، والذي يبلغ 120 فولت أو 220 فولت فقط. (26) كهرباء يمكن حساب فرق الجهد V للدائرة الكهربائية باستعمال القانون } = V، حيث: P القدرة الكهربائية، و I شدة التيار الكهربائي المار في الدائرة. a اكتب برهانا لإثبات أنه عندما تكون القدرة الكهربائية ثابتة، فإن فرق الجهد يصبح نصف ما كان عليه عندما تتضاعف شدة التيار الكهربائي. اكتب برهانا لإثبات أنه عندما تكون شدة التيار الكهربائي ثابتة، فإن فرق الجهد يتضاعف عندما تتضاعف القدرة الكهربائية. (27) تمثيلات متعددة : افترض أن مكعبًا طول ضلعه s وحدة. حسيا : ارسم أو اعمل نماذج لمكعبات أطوال أضلاعها 2 وحدة. a) جدوليا : أوجد حجم كل مكعب. نظم نتائجك في جدول مثل المجاور. (٢ لفظيًّا : استعمل الجدول لعمل تخمين حول تغير حجم المكعب عندما يتضاعف طول ضلعه. عبّر عن تخمينك لفظيًّا. (d جبريًا : اكتب تخمينك على صورة معادلة جبرية. وحدة طول الضلع (s) الحجم (V) 2 4 8 16 منطقيا : اكتب برهانًا لتخمينك . تأكد من كتابة المعطيات والمطلوب في بداية البرهان. مسائل مهارات التفكير العليا 3x + 1 6 2 (28) تحد: د : تقع النقطة P على AB. إذا علمت أن طول AP يساوي 3 + 2x، وطول PB يساوي وطول AB يساوي 10.5 وحدات ، فارسم شكلًا يوضح يوضح المسألة، وأثبت أن طول AP يساوي ثلثي طول AB. تبرير صنف الجمل الآتية إلى صحيحة أحيانًا أو صحيحة دائمًا أو غير صحيحة أبدًا. فسر تبريرك. (29) إذا كان a و b عددين حقيقيين، وكان 0 = a + b ، فإن a = b. (30) إذا كان a و b عددين حقيقيين، وكان a2 = b، فإن a = V. (31) تحد: وضعت آمنة تخمينا ينصُّ على أن مجموع أي عددين صحيحين فرديين هو عدد زوجي. a أعط أمثلة تؤيد هذا التخمين ، ثم فسر لماذا لا تُثبت هذه الأمثلة صحة التخمين. يمكن كتابة العدد الفردي على الصورة 1 - 2 . أعط أمثلة تؤيد ذلك. ما العدد الذي تكون الأعداد الزوجية جميعها مضاعفات له؟ فسّر لفظيًّا كيف يمكن استعمال إجابتك عن الفرعين لإثبات صحة التخمين. اكتب برهانًا جبريًا لإثبات أن مجموع أي عددين صحيحين فرديين هو عدد صحيح زوجي. وزارة التعليم Ministry of Education 2024-1446 الفصل 1 التبرير والبرهان 58

32 اكتب ما أوجه الشبه وأوجه الاختلاف بين البرهان الحر والبرهان ذي العمودين. أيُّ البرهانين تجده أسهل للكتابة؟ برر إجابتك. تدريب على اختبار (33 في الشكل أدناه: 90 = MCFE و LAFB = LCFD. (34) مراجعة أي علاقة يمكن أن تُستعمل لإيجاد قيم (s(n في الجدول التالي؟ n -8 -4 -10 1 s(n) 1 2 2.75 3 3.25 s(n) = 1 n + 5 n+5 C s(n) = -n + 7 A s(n) = n n+ 3 D s(n) s(n) = -2n +3 B C B A F E أي مما يأتي ليس صحيحًا بالضرورة؟ mZCFD=mZAFB C mZBFD = mZBFD A FC B محور تناظر للشكل CFE D قائمة. مراجعة تراكمية حدد ما إذا كانت كل جملة مما يأتي صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. فسّر إجابتك (الدرس 5-1) (35) أي أربع نقاط تقع في المستوى نفسه. (36) الزاويتان المنفرجتان متكاملتان. 37) المستويان P و Q يتقاطعان في المستقيم .. والمستقيم 11 يقع في كلا المستويين P و Q. حدد ما إذا كانت النتيجة صائبة أم لا في كل مما يأتي؛ اعتمادًا على العبارة التالية والمعطيات مبررًا إجابتك. ་་ يقبل العدد القسمة على 3 إذا كان يقبل القسمة على 6 الدرس (4-1) 38 المعطيات: 24 يقبل القسمة على 6. 39 المعطيات: 27 يقبل القسمة على 3. (40) المعطيات: 85 لا يقبل القسمة على 3. النتيجة : 24 يقبل القسمة على 3. النتيجة : 27 يقبل القسمة على 6. النتيجة : 85 لا يقبل القسمة على 6. 41) مبان توجد أربع بنايات في مدرسة، لا يوجد ثلاث منها على استقامة واحدة. ما عدد ممرات المشاة اللازمة لربط كل بنايتين بممر مشاةٍ واحد؟ (الدرس 5-1 استعد للدرس اللاحق أوجد طول كل قطعة مستقيمة مما يأتي مستعينًا بالشكل. BC (44 WX (43 A B C D |- 4.8 cm -in || |- الدرس 6-1 البرهان الجبري الت59م Ministry of Education 2024-1446 W X Y R S |1.2cm| | 4.0 cm ST (42 T