مبرهنتا رول والقيمة المتوسطة - الرياضيات العلمي - سادس اعدادي
الفصل الأول: الأعداد المركبة
الفصل الثاني: القطوع المخروطية
الفصل الثالث: تطبيقات التفاضل
الفصل الرابع: التكامل
الفصل الخامس: المعادلات التفاضلية الاعتيادية
الفصل السادس: الهندسة الفضائية

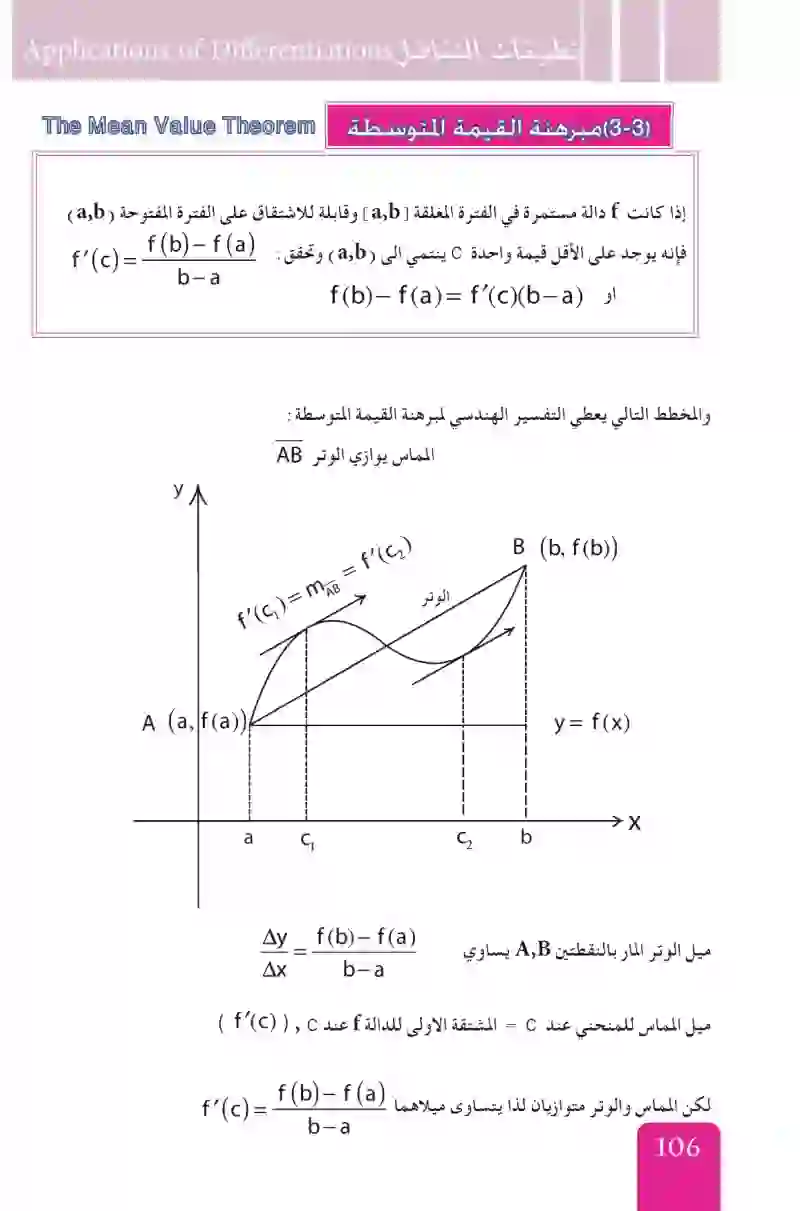
مبرهنتا رول والقيمة المتوسطة
تعريف القيمة المتوسطة







كرة نصف قطرها 6cm طليت بطلاء سمكه 0.1cm جد حجم الطلاء بصورة تقريبية باستخدام نتيجة مبرهنة القيمة المتوسطة

بين أن كل دالة من الدوال التالية تحقق مبرهنة رول على الفترة المعطاة ازاء كل منها ثم جد قيمة c f(x)=(x-1)^4,[-1,3]
![شرح بين أن كل دالة من الدوال التالية تحقق مبرهنة رول على الفترة المعطاة ازاء كل منها ثم جد قيمة c f(x)=(x-1)^4,[-1,3]](https://sahl.io/img/main/play.png)
اختبر إمكانية تطبيق القيمة المتوسطة للدوال التالية على الفترة المعطاة إزاءها مع ذكر السبب وإن تحققت المبرهنة ، جد قيم c الممكنة f(x)=x^3-x-1,[-1,2]
![شرح اختبر إمكانية تطبيق القيمة المتوسطة للدوال التالية على الفترة المعطاة إزاءها مع ذكر السبب وإن تحققت المبرهنة ، جد قيم c الممكنة f(x)=x^3-x-1,[-1,2]](https://sahl.io/img/main/play.png)