انسحاب محاور القطع الزائد - الرياضيات العلمي - سادس اعدادي
الفصل الأول: الأعداد المركبة
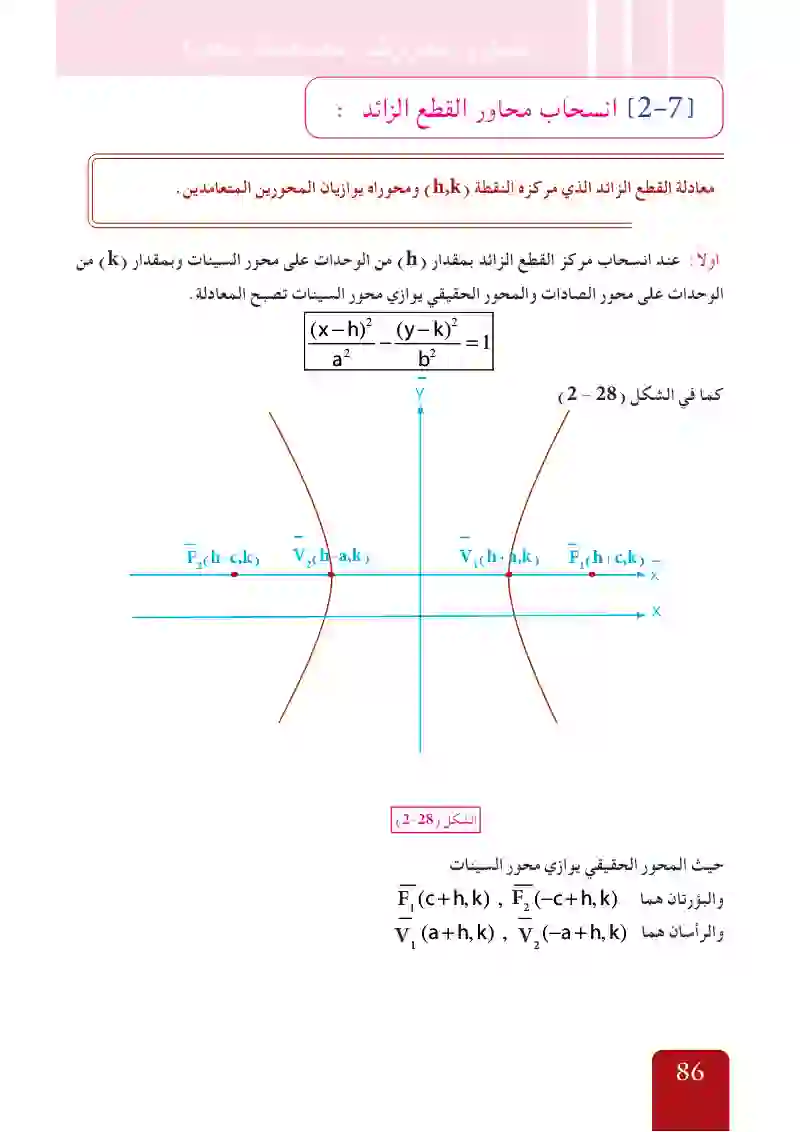
الفصل الثاني: القطوع المخروطية
الفصل الثالث: تطبيقات التفاضل
الفصل الرابع: التكامل
الفصل الخامس: المعادلات التفاضلية الاعتيادية
الفصل السادس: الهندسة الفضائية

إيجاد مركز القطع الزائد وبؤرتاه ورأساه وطول المحورين


عين كل من البؤرتين والرأسين ثم جد طول كل من المحورين والاختلاف المركزي للقطوع الزائدة الآتية 12x^2-4y^2=48

اكتب معادلة القطع الزائد في الحالات الآتية ثم ارسم القطع البؤرتان هما النقطتان (±5,0) ويتقاطع مع محور السينات عند x=±3 ومركزه نقطة الأصل

جد باستخدام تعريف معادلة القطع الزائد الذي مركزه نقطة الأصل وبؤرتيه (2√2,0),(-2√2,0) وينطبق محوراه على المحورين الإحداثيين والقيمة المطلقة للفرق بين بعدي أية نقطة عن بؤرتيه يساوي (4) وحدات

قطع زائد مركزه نقطة الأصل ومعادلته hx^2-ky^2=90 وطول محوره الحقيقي (6√2) وحدة وبؤرتاه تنطبقان على بؤرتي القطع الناقص الذي معادلته 9x^2+16y^2=576 جد قيمة كل من k,h التي تنتمي إلى مجموعة الاعدا

جد معادلة القطع الناقص الذي بؤرتاه هما بؤرتا القطع الزائد الذي معادلته x^2-3y^2=12 والنسبة بين طولي محوريه=5/3 ومركزه نقطة الأصل

جد معادلة القطع الزائد الذي بؤرتاه هما بؤرتي القطع الناقص x^2/9+y^2/25=1 ويمس دليل القطع المكافئ x^2+12y=0

النقطة (6,L)p تنتمي إلى القطع الزائد الذي مركزه نقطة الأصل ومعادلته x^2-3y^2=12 جد كلاً من أ. قيمة L



لم يتم إضافة أي تعليقات حتى الآن.
الرجاء تسجيل الدخول لكتابة تعليق