المستقيمات المتوازية والأجزاء المتناسبة - رياضيات 1 - أول ثانوي
الوحدة الأولى: الجبر والعلاقات والدوال
الوحدة الثانية: التشابه
الوحدة الثالثة: نظريات التناسب في المثلث
فكر وناقش
نظرية1
لاحظ ان
مثال حاول أن تحل1: في الشكل المقابل. س ص يوازي ب ج ، أ س = 16 سم، ب س = 12 سم.
نتيجة ص83
مثال حاول ان تحل2: في الشكل المقابل: ج هـ تقاطع ب د = (أ) ، س ينتمي الى أ د ، ص ينتمي الى أ هـ حيث س ص يوازي ب ج يوازي هـ د.
عكس نظرية1
مثال حاول أن تحل3: في الشكل المقابل: أ ب ج مثلث قائم الزاوية في أ
مثال4: أ ب ج د شكل رباعي فيه س ينمي الى أ ب ، ص ينتمي الى أ ج حيث س ص يوازي ب ج، رسم ص ع يوازي ج د ويقطع أ د في ع. أثبت أن س ع يوازي ب د
حاول أن تحل4: أ ب ج د شكل رباعي تقاطع قطراه في مـ يوازي أ د ويقطع أ ب في هـ، رسم م و يوازي ج د ويقطع ب ج في و. أثبت أن: هـ و يوازي أ ج
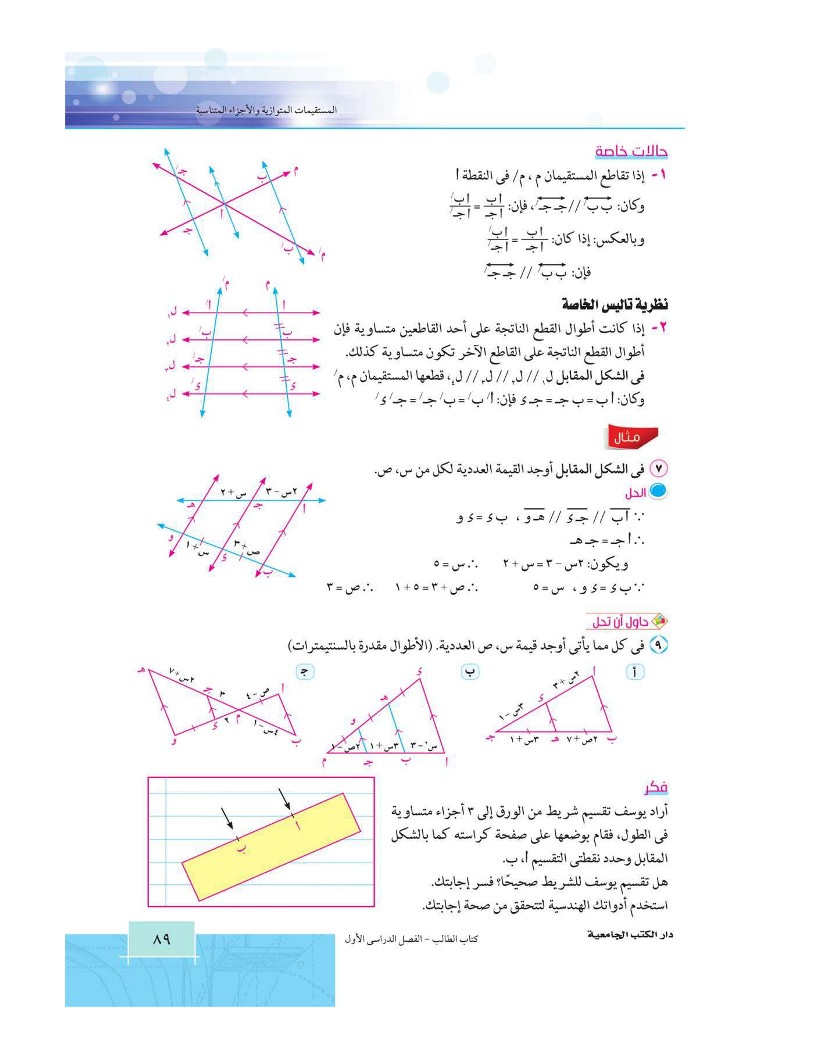
مثال5: تحديد المواقع: لتحديد الموقع ج، قام المساحون بالقياس وإعداد المخطط المقابل. أوجد بعد الموقع ج عن الموقع أ
حاول أن تحل6: مكافحة التلوث: قام فريق مكافحة التلوث بتحديد موقع بقعة زيت على أحد الشواطئ كما في الشكل المقابل. أحسب طول بقعة الزيت
فكر وناقش ص87
نظرية2
تابع نظرية2
حاول أن تحل7: اكتب ما تساويه كل من النسب التالية مستخدماً الشكل السابق:
مثال حاول أن تحل: في الشكل المقابل : أ ب يوازي ج د يوازي س ص، أ ج = 28سم، ج هـ = 20 سم ، د و = 15 سم ، و ص = 33سم أوجد طول كل من: ب د، هـ س
حالات خاصة
مثال حاول ان تحل9: في الشكل المقابل أوجد القيمة العددية لكل من س، ص.
مثال حاول أن تحل10 تحقق من فهمك: الربط بالصناعة
في الشكل المقابل د هـ يوازي ب ج. حدد العبارات الصحيحة من ما يلي:
في كل من الأشكال التالية د هـ يوازي ب ج. أوجد قيمة س العددية (الأطوال بالسنتيمترات).
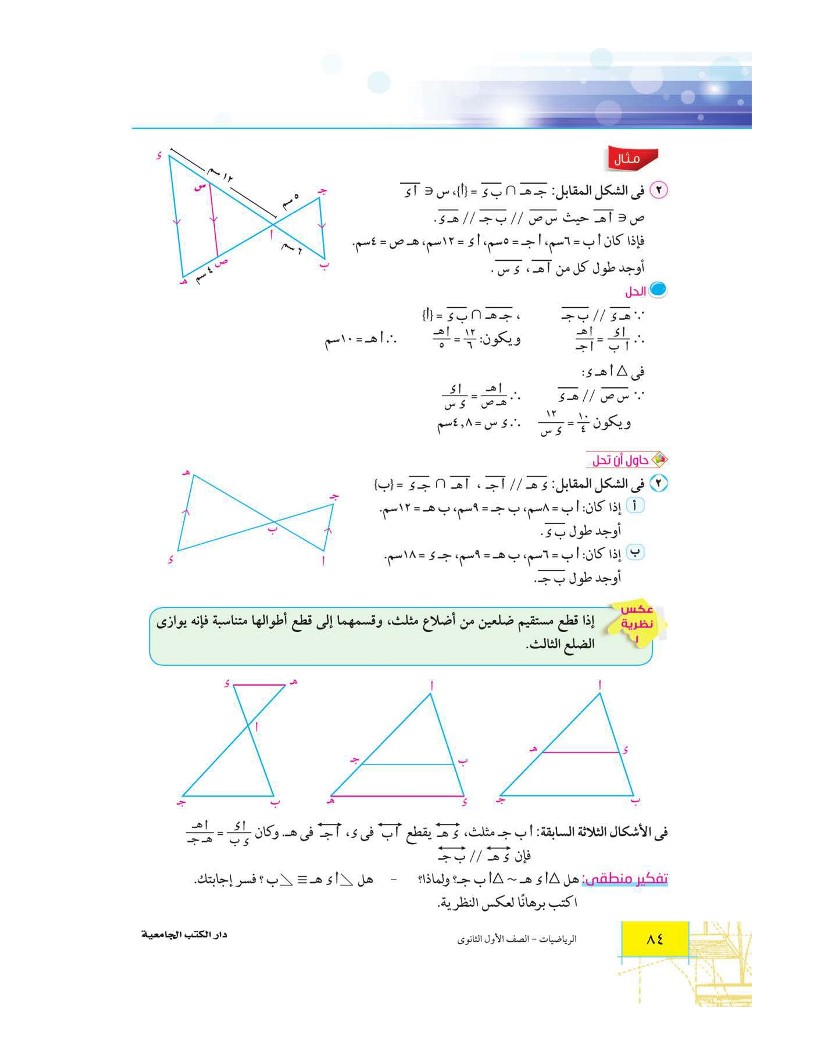
في الشكل المقابل: أ ب يوازي د هـ، أ هـ يقاطع ب د = (ج) ، أ ج = 6سم، ب ج = 4سم، ج د = 3 سم أوجد طول ج هـ
في الشكل المقابل د ه يوازي ب ج أكمل:
أ ب ج \ شكل رباعي تقاطع قطراه في هـ فإذا كان أ هـ = 6سم، ب هـ = 12 سم، هـ و = 10سم، هـ د = 7,8 سم أثبت أن الشكل أ ب ج د شبه منحرف.
س ص تقاطع ع ل = (م)، حيث س ع يوازي ل ص، فإذا كان س م = 9سم، ص م = 15سم، ع ل = 36 سم أوجد طول ع م.
لكل مما يأتي: استخدم الشكل المقابل والبيانات المعطاة لإيجاد قيمة س:
فبي كل من الأشكال التالية، حدد ما إذا كان س ص يوازي ب ج
س ص ع مثلث فيه س ص = 14 سم ، س ع = 21سم، ل ينتمي الى س ص بحيث س ل = 5,6سم، م ينتمي الى س ع حيث س م = 8.4 سم. أثبت أن ل م يوازي ص ع.
في المثلث أ ب ج، د ينتمي الى أ ب ، هـ ينتمي الى أ ج ، 5 أ هـ = 4 هـ ج ، إذا كان أ د = 10 سم، د ب = 8سم. حدد ما إذا كان د هـ يوازي ب ج. فسر إجابتك.
أثبت أن القطعة المستقيمة المرسومة بين منتصفي ضلعين في مثلث يوازي ضلعه الثالث، وطولها يساوي نصف طول هذا الضلع
أ ب ج مثلث، د ينتمي الى أ ب حيث 3أد = 3دب، هـ ينتمي الى أ ج حيث 5 ج هـ = 3 أ ج، رسم أ س يقطع ب ج في س إذا كان أ و = 8سم، أ س = 20 سم، حيث و ينتمي الى أ س. أثبت أن النقطة د،و،هـ على استقامة وا
أ ب ج د مستطيل تقاطع قطراه في م. هـ منتصف أ م ، ومنتصف م ج. رسم د هـ يقطع أ ب في س، ورسم د و يقطع ب ج في ص. أثبت أن س ص يوازي أ ج.
أ ب ج مثلث، د ينتمي الى ب ج، بحيث ب د / د ج = 3 / 4 ، هـ ينتمي الى أ د، بحيث أ هـ / أ د = 3 / 7، رسم ج هـ فقطع أ ب في س، رسم د ص يوازي ج س فقطع أ ب في ص. أثبت أن أ س = ب ص.
اكتب ما تساويه كل من النسب التالية مستخدماً الشكل المقابل:
في كل من الأشكال التالية، أحسب قيم س، ص العددية
في الشكل المقابل:
أ ب تقاطع ج د = (هـ)، س ينتمي الى أ ب ، ص ينتمي الى ج د ، وكان س ص يوازي ب د يوازي أ ج أثبت أن : أ س × هـ د = ج ض × هـ ب
في كل من الأشكال التالية، احسب قيم س، ص العددية:
أ ب ج د شكل رباعي فيه أ ب يوازي ج د ، تقاطع قطراه في م، نصف ب ج في هـ، ورسم هـ و يوازي ب أ ، ويقطع ب د في س ، أ ج في ص ، أ د في و. أثبت أن:
