القياس الستيني والقياس الدائري لزاوية - رياضيات 1 - أول ثانوي
الوحدة الأولى: الجبر والعلاقات والدوال
الوحدة الثانية: التشابه
الوحدة الثالثة: نظريات التناسب في المثلث
حلول وشروح
[1]
- حلول وشروح [2] 09:11
01:53
(2)
5
فكر وناقش القياس الدائري
تعريف الزاوية النصف قطرية
دائرة طول نصف قطرها 8سم أوجد لأقرب رقمين عشرين طول القوس إذا كان قياس الزاوية المركزية التي تقابله يساوي 5/12
العلاقة بين القياس الستيني والقياس الدائري لزاوية
حول 30 إلى قياس دائري بدلالة π
حول قياس الزاوية 1,2 إلى قياس ستيني
قمر صناعي يدور حول الأرض في مسار دائري دورة كاملة كل 3 ساعات ، إذا كان طول نصف قطر الأرض يبلغ تقريبا 6400 كم وبعد القمر عن سطح الأرض 3600 كم . فأوجد المسافة التي يقطعها القمر خلال ساعة واحدة
تابع مثال14
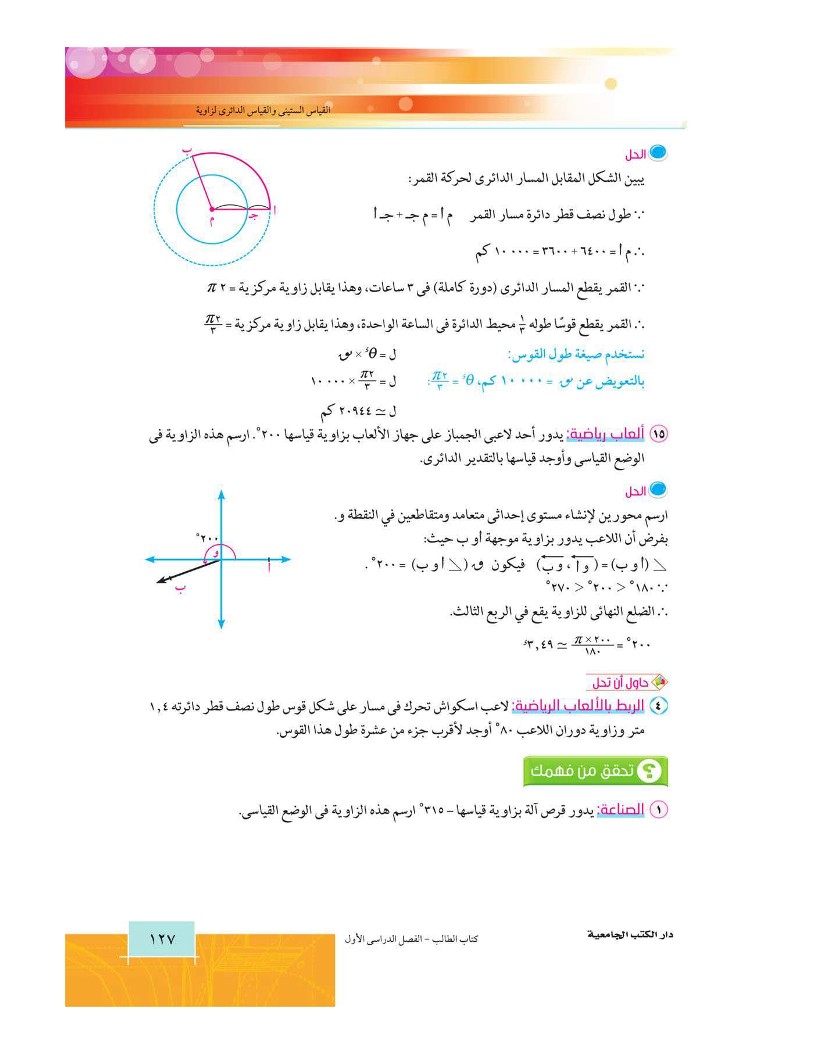
يدور أحد لاعبي الجمباز على جهاز الألعاب بزاوية قياسها 200 ارسم هذه الزاوية في الوضع القياسي وأوج\ قياسها بالتقدير الدائري
لاعب اسكواش تحرك من مسار على شكل قوس طول نصف قطر دائرته 1,4 متر وزاوية دوران اللاعب 80 أوجد لأقرب جزء من عشرة طول هذا القوس
اختيار من متعدد
أوجد القياس الستيني للزوايا التي قياسها كالآتي مقربا الناتج لأقرب ثانية
الشكل المقابل إذا كان مساحة المثلث م أ ب القائم الزاوية في م =32 سم " فأوجد محيط الشكل المظلل مقربا الناتج لأقرب رقمين عشريين
دائرة طول نصف قطرها 4سم , رسمت الزاوية أ ب ج المحيطية التي قياسها 30 أوجد طول القوس الأصغر أ ج
مثلث قياس إحدى زواياه 60 وقياس زاوية أخرى منه يساوي π/4 , أوجد القياس الدائري والقياس الستيني لزاويته الثالثة
أوجد القياس الدائري والقياس الستيني للزاوية المركزية التي تقابل طوله 8,7 سم في دائرة طول نصف قطرها 4 سم
زاوية مركزية قياسها 150 وتحصر قوسها طوله 11 سم احسب طول نصف قطر دائرتها
إذا كان قياس زاوية مركزية في دائرة طول قطرها نق وتحصر قوسا طوله ل:
أوجد القياس الدائري للزوايا التي قياسها كالاتي مقربا الناتج لثلاثة أرقام عشرية
أوجد بدلالة π القياس الدائري للزوايا التي قياسها كالاتي
مستقيم يصنع زاوية قياسها π/3 في الوضع القياسي لدائرة الوحدة مع التجاه الموجب لمحور السينات أوجد معادلة هذا المستقيم
تستخدم المزولة الشمسية لتحديد الوقت أثناء النهار من خلال طول الظل الذي يسقط على سطح مدرج لإظهار الساعة وأجزائها ، فإذا كان الظل يدور على القرص بمعدل 15 " لكل ساعة أوجد قياس الزاوية بالرديان ا
في الشكل المقابل : أب ، أج مماسان للدائرة م ، ق ( الزاوية ج أ ب ) = 60 ، أ ب = 12 سم . أوجد لأقرب عدد صحيح طول القوس الأكبر ب جـ .
قمر صناعي يدور حول الأرض في مسار دائري دورة كاملة كل 6 ساعات ، فإذا كان طول نصف قطر مساره عن مركز الأرض 9000 كم ، فأوجد سرعته بالكيلومتر في الساعة
كم المسافة التي تقطعها نقطة على طرف عقرب الدقائق خلال 10 دقائق إذا كان طول هذا العقرب 6 سم؟
أ ب قطر في دائرة طوله 24 سم ، رسم الوتر أجـ بحيث كان ق ( الزاوية ب ا جـ ) = 50 أوجد طول القوس الأصغر أ ج مقربا الناتج لأقرب رقميين عشريين .
لم يتم إضافة أي تعليقات حتى الآن.
الرجاء تسجيل الدخول لكتابة تعليق
