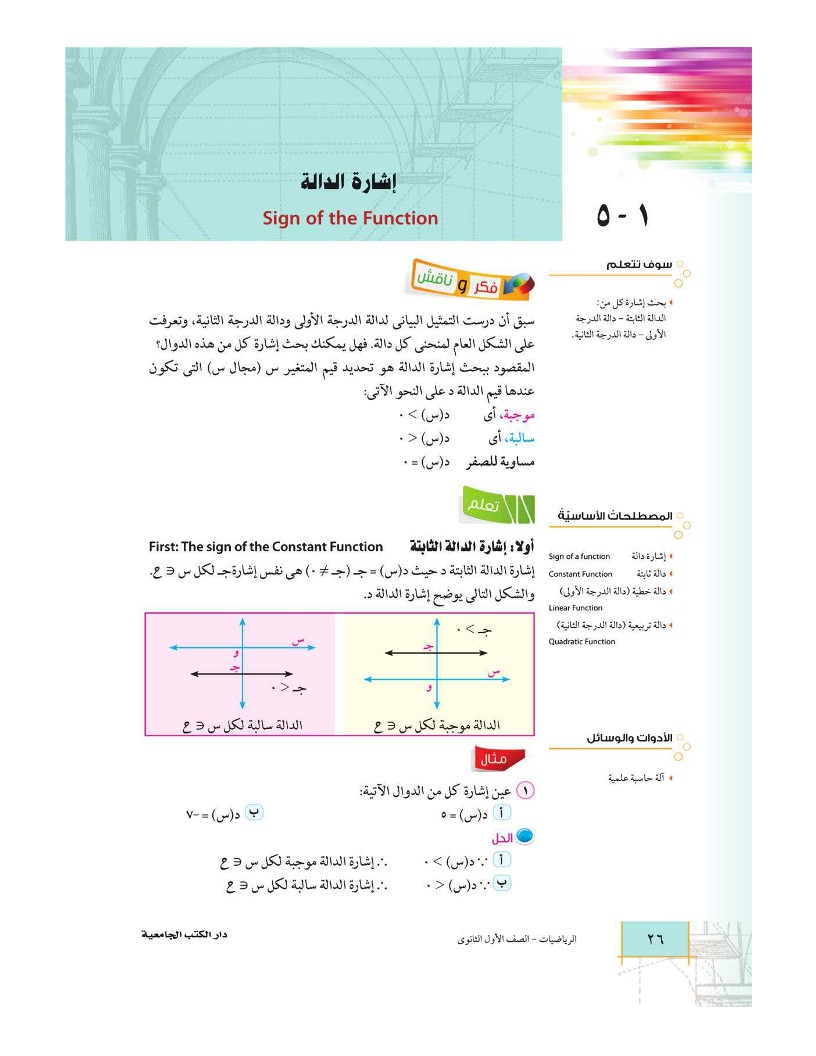
إشارة الدالة - رياضيات 1 - أول ثانوي
الوحدة الأولى: الجبر والعلاقات والدوال
الوحدة الثانية: التشابه
الوحدة الثالثة: نظريات التناسب في المثلث
أحمد سرور
[1]
- أحمد سرور [2] 07:03
- أحمد سرور [3] 00:50
- ناصر سالم [1] 02:32
- ناصر سالم [2] 01:42
- ناصر سالم [3] 02:31
- احمد زيدان [1] 01:15
- احمد زيدان [2] 02:46
- محمد امين [1] 01:03
- محمد امين [2] 03:54
- شيماء محمد 00:55
- طارق الفرارجي 02:17
- حلول وشروح [1] 01:18
- حلول وشروح [2] 01:23
00:45
(0)
0
فكر وناقش تعلم أولاً إشارة الدالة الثابتة
مثال1: عين إشارة كل من الدوال الآتية:
حاول أن تحاول1: عين إشلرة كل من الدوال الآتية:
ثانياً إشارة دالة الدرجة الأولى
مثال حاول أن تحاول2: عين إشارة الدالة د حيث د(س) = س - 2 مع توضيح ذلك بيانياً:
ثالثاً إشارة الدالة التربيعية
مثال حاول أن تحاول3 مثل بيانيا د، حيث د(س) = س² - 2س - 3 ثم عين إشارة الدالة د.
ثانياً : إذا كان ب²- 4أ جـ أكبر من 0 فإنه لا توجد جذور حقيقية، وتكون إشارة الدالة د مثل إشارة معامل س²، والأشكال التالية توضع ذلك.
مثال: مثل بيانياً د حيث د(س) = س² - 4س + 5 ثم عين إشارة الدالة د.
ثالثاً: إذا كان ب² - 4أج = فإنه يوجد للمعادلة جذران متساويان، وليكن كل منهما يساوي ل، وتكون إشارة الدالة د كالآتي:
مثال حاول أن تحل5: مثل بيانياً د حيث د(س) = 4س² - + 1، ثم عين إشارة الدالة د
مثال 6 أثبت أ،ه لجميع قيم س ينتمي الى ح يكون حذرا المعادلة 2س² - ك س + ك - 2 = صفر حقيقيين مختلفين
تحقق من فهمك: عين إشارة كل دالة من الدوال الآتية:
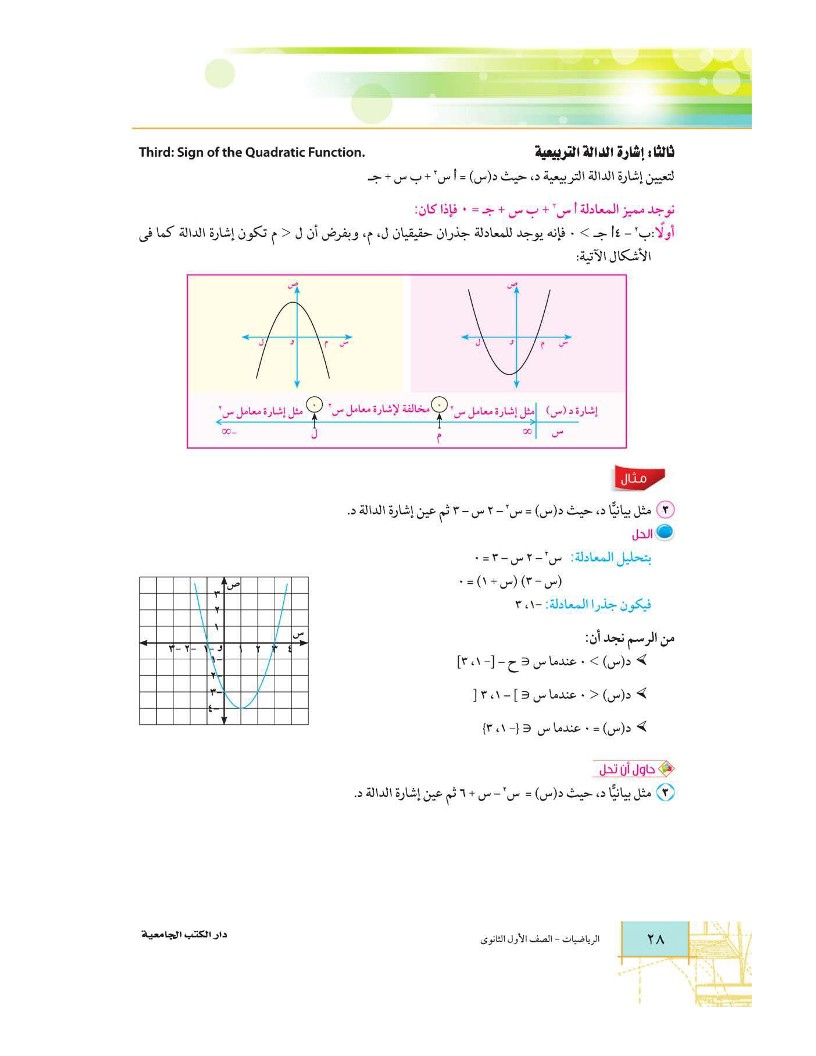
في التمارين من أ إلى ن عين إشارة كل من الدوال الآتية:
أولاً: أكمل ما يأتي:
مناجم الذهب: في الفترة من عام 1990 إلى 2010 كان إنتاج أحد مناجم الذهب مقدراً بالألف أوقية يتحدد بالدالة د: د(ن) = 12ن² - 96 ن + 480 حيث ن عدد السنوات، د(ن) انتاج الذهب
اكتشف الخطأ: إذا كانت د(س) = س + 1، ر(س) = 1-س² فعين الفترة التي تكون فيها الدالتان موجبتين معاً.
ارسم منحنى الدالة د(س) = -س² + 2س +4 في الفترة[-3، 5]ومن الرسم عين إشارة د(س).
ارسم منحنى الدالة د(س) = س² -9 في الفترة [-3 ، 5]، ومن الرسم عين إشارة د(س).
تابع تمارين (1-5)
لم يتم إضافة أي تعليقات حتى الآن.
الرجاء تسجيل الدخول لكتابة تعليق
